为什么自然界中超剪切破裂的地震是如此之少？

朱守彪，崔泽飞2,

1 应急管理部国家自然灾害防治研究院，北京 100085 2 中国地震局地球物理研究所，北京 100081

0 引言

自从1979年美国加州帝王谷MW6.5地震(Imperial Valley earthquake)被识别为超剪切破裂地震(Olson and Apsel,1982;Archuleta,1984;Spudich and Cranswick,1984)以来，科学家们陆续发现了一系列新的地震为超剪切破裂地震，例如：1999年土耳其Izmit 地震(MW7.6)(Bouchon et al.,2000),1999年土耳其 Düzce地震(MW7.2)(Bouchon et al.,2001；Bouin et al.,2004;Konca et al.,2010),2001年中国昆仑山地震(MS8.1)(Bouchon and Vallée,2003;Antolik et al.,2004;Robinson et al.,2006;Vallée et al.,2008;Vallée and Dunham,2012),2002年美国阿拉斯加 Denali地震(MW7.9)(Dunham and Archuleta,2004；Ellsworth et al.,2004),2010年中国玉树地震(MW6.9)(Wang and Mori,2012；Wang et al.,2016),2012 年印度洋地震(MW8.6)(Wang et al.,2012),2013年美国阿拉斯加Craig地震(MW7.5)(Yue et al.,2013),2014年爱琴海北部地震(MW6.9)(Evangelidis,2015),2018年印度尼西亚Palu地震(MW7.5)(Bao et al.,2019;Lee et al.,2019;Socquet et al.,2019),2018年洪都拉斯Swan Island地震(MW7.5)(Cheng and Wang,2020),2020年加勒比海地震(MW7.7)(Tadapansawut et al.,2021),以及2013年鄂霍次克海地震(MW8.3)的强余震(MW6.7)(Zhan et al.,2014).

当发生超剪切地震破裂时，不同时刻所有破裂前端产生的地震波同时到达一定区域，并发生相长干涉，形成马赫锥，从而导致马赫波振幅显著增大，相应的地震动幅度也大大增强，从而加重地震灾害(Bernard and Baumont,2005；Dunham and Bhat,2008；Andrews,2010；Cruz-Atienza and Olsen,2010；胡进军和谢礼立,2011；Vallée and Dunham,2012；Yue et al.,2013 ;徐建宽,2014;朱守彪等,2017；Zhu,2018;朱守彪和袁杰,2018;Zhu and Yuan,2020).因此，超剪切破裂地震的研究一直受到十分广泛的重视.

但是，从上述的震例可以看到，到目前为止自然界中被人们识别为超剪切破裂的地震仅有十多个，显然其数量非常稀少.为什么会产生这种现象？是哪些因素造成了超剪切破裂地震是如此之少？这个科学问题，至今未见前人有系统的分析和研究，本文利用有限单元的计算方法，试图定量地对此现象进行分析并给出科学解释.

关于超剪切破裂形成机理的经典理论是Burridge-Andrews机制(简称B-A机制)(Burridge,1973;Andrews,1976a,b).在B-A机制中，以亚剪切波传播的主破裂，子破裂(daughter rupture)在其前方成核，其后子破裂很快就以超剪切波速度传播，从而形成超剪切破裂.前人的研究表明，一个在全空间中断层直立的面上行进的走滑型破裂(即破裂不会穿透到地表)，当介质属性及初始应力均匀时，若初始应力水平足够高，亚剪切破裂就有可能转换为超剪切破裂，并用S值来定量表达.S值可以表示为：S=(τp-τ0)/(τ0-τr)，其中，τ0表示断层面的初始剪切应力，τp和τr分别表示断层的应力强度以及破裂滑动后剩余的剪切应力(Andrews,1976a,b;Das and Aki,1977).对于二维无限弹性空间无界平面应变走滑断层模型，当S<1.77就可以产生超剪切破裂；但对于三维情况，需要更高的初始应力，只有当S<1.19时才产生超剪切破裂(Andrews,1985;Dunham,2007).

对于实际的地震破裂过程，研究中发现还有诸多因素可以导致超剪切破裂的发生，比如：破裂之前非均匀的应力场空间分布(如，Fukuyama and Olsen,2002;Dunham et al.,2003;Duan and Oglesby,2006;Liu and Lapusta,2008),不均匀的断层几何形状(如,Oglesby and Mai,2012;Bruhat et al.,2016;Tadapansawut et al.,2021),断层阶区(如,Ryan and Oglesby,2014;Hu et al.,2016;袁杰和朱守彪,2017),断层弯折(如,Poliakov et al.,2002;Oglesby and Mai,2012;Zhu,2018;Zhu and Yuan,2020),断层障碍体 (如,Dunham et al.,2003;Latour et al.,2013;Weng et al.,2015;Xu et al.,2016),断层两侧介质物性差异(如,Xia et al.,2005;Shi and Ben-Zion,2006;Langer et al.,2012;Shlomai and Fineberg,2016;Shlomai et al.,2020),等等.另外，还有一个产生超剪切破裂的重要因素是地球的自由表面(如,Olsen et al.,1997;Aagaard et al.,2001;Zhang and Chen,2006;Kaneko et al.,2008;Kaneko and Lapusta,2010;Xu et al.,2015;Hu et al.,2019,2020).正如Hu等(2020)所指出的，在所有产生超剪切破裂的机制中，地球自由表面的效率最高，而且要高很多.特别是，Xu等(2015)声称，对于一个具有自由表面的走滑型断层破裂，只要断层足够长，那么这个破裂最终都会演化为超剪切破裂.可以想象，若Xu等(2015)的结果是正确的话，那么自然界里的超剪切破裂将比实际情况要多得多.因此，为什么大部分破裂到地表的走滑型断层破裂最终没有演化为超剪切破裂呢？主要的原因可能是，Xu等(2015)在模型中假定，介质材料属性均匀，初始应力均匀分布，并且整个断层都受滑移弱化的摩擦本构关系所控制(Ida,1972;Andrews,1976a,b;Ohnaka and Yamashita,1989;Bizzarri,2011;Ohnnaka,2013).的确，在这样的简化模型中，走滑型断层破裂都可以演化为超剪切破裂(Kaneko and Lapusta,2010;Xu et al.,2015).然而，真实的地震断层，特别是在近地表区域，由于存在一定厚度的沉积层、断层泥、断层带内破碎的岩石以及正应力水平低等因素，地表附近的断层介质往往是速度强化的摩擦关系(如,Shimamoto and Logan,1981;Marone and Scholz,1988;Marone et al.,1991;Unsworth et al.,1997;Marone,1998;Scholz,1998;Lyons et al.,2002;Shearer et al.,2005;Kaneko et al.,2008，2013;Cochran et al.,2009;Wei et al.,2013).并且这个地表速度强化的摩擦关系介质，其厚度通常达到3～5 km(如，Marone and Scholz,1988;Marone et al.,1990;Unsworth et al.,1997;Ben-Zion and Sammis,2003;Barbot et al.,2009;Zhang et al.,2009;Wei et al.,2013;Ampuero and Mao,2017).

鉴于上述分析，本文运用有限单元方法，首先考虑模型中近地表具有一定厚度的速度强化的摩擦关系介质，考察这种速度强化层对破裂传播过程的影响；然后，进一步研究断层上的障碍体、阶区、反凹凸体等对超剪切破裂的作用；最后，综合分析自然界中产生可以识别的超剪切破裂地震的条件，以及为什么超剪切破裂的地震是如此之少的动力学机制.

1 地表附近速度强化的摩擦关系介质对破裂过程的影响

为考察、对比地表附近速度强化的摩擦关系介质对断层自发破裂过程的影响，我们构建了2个三维的有限单元模型.在模型1中，整个断层面上的摩擦关系空间分布均匀并且都是滑移弱化的摩擦本构关系；模型2中，地表附近2 km以内为速度强化的摩擦关系，2 km以下的断层面上仍由滑移弱化的摩擦关系所控制.

1.1 有限元模型及参数设定

三维有限元的模型几何见图1a，直立的走滑型断层长度为60 km,宽度为15 km；材料假定为线弹性介质，其剪切波速度VS=3294 m·s-1，纵波速度VP=5959 m·s-1,泊松比为0.25；介质密度ρ=2700 kg·m-3(见表1).图中红色的条带代表厚度为2 km的地表，受速度强化的摩擦关系所控制；断层上的白色区域为滑移弱化的摩擦本构关系.此外，我们知道，在求解断层自发破裂传播过程这类高度非线性的问题中，初始应力及边界条件起着非常重要的作用.然而，我们对地下深处应力状态知之甚少，所以参照前人的做法(Rice,1993;Ben-Zion and Rice,1997,Kaneko et at.,2008)，断层面上的初始剪应力和有效正应力分布如图1b所示.

图1 三维有限元模型几何及初始应力分布图(a)中的红色条带区域表示受速度强化的摩擦关系控制，下面的白色区域是滑移弱化的摩擦关系；(b)断层面上的初始有效正应力及剪切应力随着深度的变化曲线(S=1.6).Fig.1 A 3-D model geometry and initial stresses applied in the finite element model(a)The red belt shown in the figure is governed by the velocity-strengthening friction law,and the area in white is governed by slip-weakening frictional relation.(b)The initial effective normal stress and shear stress change with the increase of depth (S=1.6).

另外，为提高计算效率，保证计算精度，有效分辨破裂凝聚区(cohesive zone),有限元网格剖分时，断层面附近单元边长取60 m,模型最外部单元边长取100 m.此外，除了地表及断层面上，模型所有外围均施加吸收单元，目的是有效防止地震波的反射(DeDontney et al.,2012;袁杰和朱守彪,2017;Zhu,2018).

有限元模拟中，摩擦关系决定着断层自发破裂的特征，研究中选择目前应用最为广泛的线性滑移弱化的摩擦本构关系(Ida,1972;Palmer and Rice,1973;Andrews,1976a,b;Ohnaka and Yamashita,1989)，其摩擦系数的数学表达式如下：

(1)

(1)式中，μs表示静摩擦系数，μd表示动摩擦系数，Dc表示特征滑动距离，u表示滑动距离.具体参数大小选择见表1.

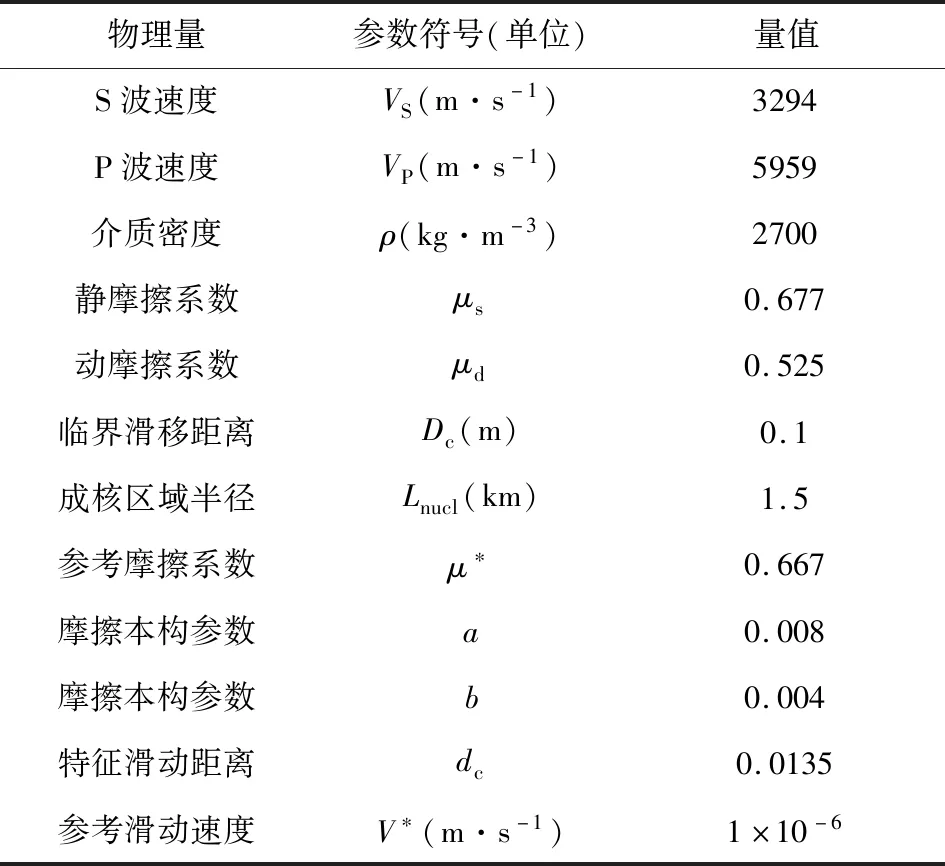
表1 模型中的材料参数、初始应力场及摩擦参数Table 1 Material parameters,initial stresses and frictional parameters used in the model

另外，除了上述滑移弱化的摩擦关系外，还有一种应用也十分广泛的摩擦本构关系，就是速率-状态相依的摩擦关系(如，Dieterich,1979a,b,1994;Beeler et al.,1994;Blanpied et al.,1998;Mair and Marone,1999;Bizzarri and Cocco,2005；Bizzarri，2011).摩擦系数μ的数学表达式如下：

(2)

(2)式中，V是滑移速率，θ表示断层摩擦的状态量;a,b为摩擦本构参数；dc表示特征滑动距离,V*为参考滑动速度，μ*为稳态时的参考摩擦系数.

由于状态量θ有多种多样的演化方式，这样速率-状态相依的摩擦本构关系就有多种不同的形式.但目前在数值计算中有两种最为常用的定律,一种称之为老化定律(aging law)(Dieterich,1981)，另一种为滑移定律(slip law)(Ruina,1983).它们分别可以用下列数学公式来表示：

(3)

(4)

(5)

从(5)式不难看出，若a-b>0时，表示速度强化的摩擦关系，即摩擦系数随着滑动速度的增大而增大(Rice and Ruina,1983;Ruina,1983)；但当a-b<0时,表示速度弱化的摩擦关系.需要说明的是，本文中我们省略了“稳态(steady state)”的字样，一律简称为速度强化/弱化的摩擦关系.

研究中，实际有限元计算利用大规模商业有限元软件Abaqus来进行.为保证获得稳定收敛的解，计算的时间步长取为0.0001 s.同时，模拟开始时，让断层两盘以2.0×10-13m·s-1的速度做等速反向运动，该速度远远低于典型的板块运动速度.另外，图2中的红色五角星表示成核位置，坐标位于(10 km,0,-7.5 km)，圆形成核区的半径为1.5 km.模拟中是通过降低摩擦系数来成核，并产生断层的自发破裂(朱守彪等，2017；朱守彪和袁杰，2018).

1.2 模拟结果

为考察对比地表附近速度强化的摩擦关系对破裂过程的影响，我们构建了两个三维有限单元模型.这两个模型的几何尺寸、网格剖分、初始应力分布、介质物理性质等都是完全一样的，所不同的是断层面上的摩擦关系.模型1中整个断层面上的摩擦关系均为滑移弱化的(见图2a)；而模型2中断层面上方、近地表附近2 km范围内(图中的红色条带)，摩擦关系为速度强化的，但2 km下方的白色区域和模型1中的摩擦关系完全一样，为滑移弱化的摩擦关系(见图2b).

图2为有限元计算给出的两个模型断层自发破裂传播过程中，在不同时刻质点振动速度等值线图的快照.图2a表示模型1的计算结果，图2b表示模型2的结果.通过两图对比很容易看到，模型1的结果出现了二次破裂(即主破裂之前的第二个新破裂)，但模型2的结果没有见到二次破裂.经过计算发现，二次破裂的传播速度为5097 m·s-1，远远大于剪切波速度(VS=3294 m·s-1).显然，这个二次破裂为超剪切破裂；但是整个断层面上的S=1.6，高于B-A机制中产生超剪切破裂的临界S值(S=1.19)(Dunham,2007).这正说明地球自由表面在促使亚剪切转化为超剪切破裂方面是高效率的，这与Xu等(2015)以及Kaneko等(2008)的计算结果具有非常好的一致性.同时，也从另一方面说明文中的模拟结果是稳定可靠的.另外，图2b中的结果没有出现图2a中的超剪切破裂，同样通过计算也得到，图2b中的主破裂的传播速度为3043 m·s-1，低于剪切波的传播速度，属于亚剪切破裂.

图2 模型1和模型2的断层几何及破裂在不同时刻的快照图(a)代表模型1的结果,(b)代表模型2的结果.显然，模型1中出现了二次破裂，产生了马赫波，破裂速度为5097 m·s-1，为超剪切破裂；而模型2中没有出现二次破裂，破裂速度为3043 m·s-1，为亚剪切破裂.底图为规则化的破裂速度(VR/VS)等值线分布图，红色表示超剪切破裂.Fig.2 Fault geometries and snapshots of rupture scenarios at different times both in Model 1 and in Model 2(a)represents the results from Model 1 and (b)from Model 2.It is evident that the secondary rupture is observed in Model 1,producing Mach waves with the rupture speed of 5097 m·s-1,larger than S wave velocity,indicating supershear rupture;while in Model 2 no second rupture is observed,with rupture velocity of 3043 m·s-1,belong to subshear rupture.At the bottom of figure is displayed the spatial contour distribution of normalized rupture speed (VR/VS),with the red standing for supereshear rupture velocity.

上述两个模型中一个产生了超剪切破裂，而另一个只产生亚剪切破裂，两者唯一的区别只是在于地表附近的摩擦本构关系，模型2在其上地表存在一个2 km厚的速度强化层，而模型1整个断层面上的摩擦关系都是滑移弱化的.可见，正是这个2 km厚的摩擦速度强化层完全阻止了超剪切破裂的产生.

那么，真实的自然界中，这个速度强化层的厚度大小及其分布格局将在一定程度上决定着超剪切破裂地震的大小及数量.

实际的断层表层(通常指3 km以内的浅地表)，由于存在一定厚度的沉积层、断层泥、断层带内未固结的松软介质、地震作用导致的岩石破碎、孔隙含水介质断层带内有效正应力水平低等因素，导致浅地表地震活动很弱(因此在摩擦强化区，破裂无法成核而不能形成地震)、断层发生震间蠕变、震后余滑等现象，这些都是介质属于摩擦速度强化的具体力学表现(如，Marone and Scholz,1988;Marone et al.,1990,1991;Unsworth et al.,1997;Barbot et al.,2009;Zhang et al.2009;Kaneko et al.,2008,2013;Wei et al.,2013;Ampuero and Mao,2017).

然而，对于实际的断层而言，情况非常复杂，近地表摩擦速度强化层的厚度是变化的，强化层内摩擦本构关系中的参数也可能是不同的；此外沿着断层走向方向，强化层厚度及摩擦本构参数都可能是不均匀的，所以对于具体的断层，要根据实际地震地质考察结果进行数值模拟.但可以肯定的是，2 km厚的地表速度强化层可以有效地抑制超剪切破裂地震的发生.

2 断层阶区、障碍体及反凹凸体对断层自发破裂过程的影响

我们知道，断层阶区、断层上的障碍体及反凹凸体对断层的破裂传播特征及破裂传播速度有重要的影响(如，Harris and Day,1993;Dunham et al.,2003;Page et al.,2005;Ryan and Oglesby,2014;Weng et al.,2015;Xu et al.,2016;袁杰和朱守彪,2017).下面我们利用有限元方法，定量分析这些因素对破裂传播过程，特别是超剪切破裂过程转化的影响.在以下不同的有限元模型中，介质都假定为线弹性，介质的剪切波速度设定为VS=3330 m·s-1，纵波速度为VP=5770 m·s-1,泊松比为0.25；介质密度ρ=2700 kg·m-3；断层面上施加的初始剪应力都为56 MPa,初始有效正应力为 100 MPa，成核半径为 2 km.由于篇幅限制，有限元模型及模拟细节不再赘述，详细请参看作者以前的文章(朱守彪等，2017；朱守彪和袁杰，2018，Zhu,2018;Zhu and Yuan,2020).

2.1 断层阶区对破裂过程的影响

前人的研究表明，断层阶区对地震破裂过程有重要影响：一方面，断层阶区有可能会阻碍地震破裂，阻止破裂由一条断层跨越到另一条断层而继续传播；另一方面，在一定条件下，破裂也可能会越过断层阶区而继续前行(Harris and Day,1993；Ryan and Oglesby,2014;袁杰和朱守彪,2017).下面利用有限单元方法，对断层阶区影响破裂传播过程进行定量分析，特别考察破裂在跨越断层阶区前后的破裂速度以及其中间的时间历程.

图3是断层阶区的几何尺寸，初始断层(破裂成核的断层)长度为35 km,次级断层长度也为35 km,断层间距为1.0 km.两条断层都受滑移弱化的摩擦关系所控制，其中静摩擦系数μs=0.639，动摩擦系数μd=0.519，特征滑动距离Dc=0.1 m.

图3 断层阶区的几何.初始断层及次级断层长度都为35 km,阶区宽度为1.0 km红色区段表示成核位置.Fig.3 Geometry of the fault step-over.The length of the primary and secondary faults is 35 km,and the width of the step-over is 1.0 kmThe red patch stands for the nucleation zone.

图4为有限元计算给出的破裂过程在不同时刻的快照.图中显示，破裂开始后，先在第一条断层上向两侧传播，传播的速度为1932 m·s-1，低于剪切波速度(其值为VS=3330 m·s-1)，大约经历8 s左右的时间第一条断层上的破裂就基本完成；此后，第一条断层破裂产生的应力波继续前行(见图4c—i).但是断层破裂就此停顿.大约在破裂开始后14.5 s的时刻(见图4e)，在次级断层上成核新的破裂；然后新的破裂经过不断演化，自发向前传播(见图4f—j).期间破裂停止的时间为6～7 s.图中清晰地显示，在次级断层上，破裂过程中出现了马赫波，说明在次级断层上的破裂为超剪切破裂.确实，经过计算得到在次级断层上的破裂速度为5502 m·s-1，其值远远大于剪切波的速度，为超剪切破裂.但是，通过计算发现整个断层上的平均破裂速度只有2531 m·s-1，其值仍低于剪切波的速度.所以，断层阶区尽管可以促使超剪切破裂的发生，但在远场看来整个破裂仍是亚剪切破裂，除非在近场有足够的地震台站可以进行有效的辨别.

图4 破裂跨过断层阶区时，不同时刻破裂传播的快照.图中可见，在t=14.5 s时，新的破裂在次级断层上成核，其后不断演化，形成马赫波，产生超剪切破裂.但破裂跨越断层阶区时，出现破裂停顿的现象，导致整个破裂过程平均为亚剪切破裂Fig.4 Snapshots of different times in the process of the rupture propagation with fault stepover.It is seen in the figure that new rupture nucleated on the secondary fault at t=14.5 s,then evolved incessantly to form Mach waves,resulting in supershear rupture.While in propagating across the stepover,the rupture suspended for some times,giving rise to subshear rupture speed averaged in the whole rupture propagation

2.2 障碍体对破裂过程的作用

断层上的障碍体通常是位于断层端部、断层不连续段或摩擦强度很大的区域，一般情况下，障碍体都是阻止破裂继续扩展的.但在有些特殊条件下，障碍体不仅不会阻碍断层破裂继续前行，反而还将原来的亚剪切破裂转化为超剪切破裂(Dunham et al.,2003；Latour et al.,2013;Weng et al.,2015;Xu et al.,2016).为方便起见，下面构建一个二维的有限单元模型，通过计算来说明障碍体是如何将亚剪切破裂转化为超剪切破裂，转化过程中会出现哪些特殊现象.

图5是障碍体的几何模型结构，断层长度为40 km,障碍体的长度取为8 km.整个断层受滑移弱化的摩擦关系所控制：障碍体外部断层上的静摩擦系数μs=0.620，动摩擦系数μd=0.525，特征滑动距离Dc=0.1 m；但在障碍体内部，静摩擦系数μs=0.76，动摩擦系数μd=0.57，Dc=0.1 m.

图5 断层上存在障碍体的几何结构黄色小方块代表成核区，红色代表障碍体.Fig.5 Geometry of fault structure with barrierThe yellow patch represents nucleation zone,the red stands for barrier.

同样，利用有限元计算可以得到断层破裂穿过障碍体时整个过程的图像.图6为破裂成核后，破裂传播过程在不同时刻的快照.如图所示，破裂在到达障碍体之前，破裂速度为2011 m·s-1，低于介质中剪切波的传播速度(3330 m·s-1)，显然为亚剪切破裂；但当破裂突破障碍体后，图中清晰地显示，出现了马赫波，破裂速度为5507 m·s-1,为超剪切破裂.这与前人的结果类似(如,Dunham et al.,2003;Weng et al.,2015;Xu et al.,2016).

但是，图中显示，在破裂突破障碍体的过程中，大约有3～4 s的时间停留(见图6c—d)，这样在整个断层上，平均的破裂传播速度只有2916 m·s-1，仍为亚剪切破裂.与断层阶区类似，远场可能还是难以辨别由于障碍体产生的局部超剪切破裂事件.除非这个超剪切破裂传播很长的距离(地震震级很大)或近场附近正好有足够密集的地震台站，不然很难辨别这个障碍体导致的超剪切破裂.也许自然界中超剪切地震很普遍，但是由于我们可能“看不见”，导致超剪切破裂地震很稀少的现象.

图6 破裂穿过障碍体过程中不同时刻的快照Fig.6 Snapshots of different times in the process of the rupture propagation with barrier

2.3 反凹凸体对破裂过程的影响

断层上的反凹凸体通常是指断层内部应力水平较低的区域.由于应力水平较低，距离破裂所需的应力水平差距较大，所以在一般情况下，反凹凸体也是阻止断层破裂继续传播的因素(Dunham et al.,2003；Page et al.,2005).但是，与障碍体情况类似，当亚剪切破裂突破反凹凸体的阻挡后，有时可以将亚剪切破裂转化为超剪切破裂.下面利用有限单元方法，模拟亚剪切破裂通过反凹凸体的破裂过程，研究破裂特征的变化(模型几何见图7).有限元模拟时，假定整个断层受滑移弱化的摩擦关系控制，静摩擦系数μs=0.620，动摩擦系数μd=0.525，特征滑动距离Dc=0.1 m；反凹凸体内部的剪切应力减小为50.8 MPa.

图7 断层上存在反凹凸体的几何结构图红色小方块代表成核区，蓝色代表反凹凸体.Fig.7 Geometry of fault structure with anti-asperityThe red patch represents nucleation zone,the blue stands for anti-asperity.

与前面的情况类似，利用有限元方法模拟可以得到断层破裂通过反凹凸体时整个破裂过程的图像.图8为破裂成核后，破裂传播过程在不同时刻的快照.由图8可见，破裂在到达反凹凸体之前，破裂速度为2011 m·s-1，为亚剪切破裂；但当破裂越过反凹凸体后，图中清晰地显示，出现了马赫波，并且可以通过计算导出破裂速度为5501 m·s-1,该速度大于剪切波的速度，这意味着此时的断层破裂为超剪切破裂.这种情况也与前人的结果相似(如，Dunham et al.,2003).值得注意的是，破裂穿过反凹凸体时的速度特征与穿过障碍体时几乎一样，这可能与模型参数的选取有关，详细过程还有待于深入研究.

图8结果还显示，在破裂通过反凹凸体的过程中，也同样出现时间暂停现象，破裂大约停止了4 s的时间，这样在整个断层上，破裂的平均传播速度为2693 m·s-1，仍然为亚剪切破裂.与断层阶区、断层障碍体类似，远场可能还是难以辨别由于反凹凸体产生的局部超剪切破裂过程.除非凹凸体前方的断层长度很长(震级很大)，或近场附近有足够密集的地震观测台站，不然很难识别这个由于反凹凸体产生的超剪切破裂事件.因此这也许是自然界中超剪切破裂地震很少的另一个原因.

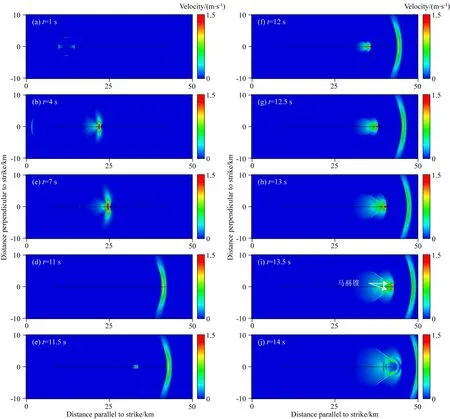
图8 破裂通过反凹凸体过程中不同时刻的快照.破裂过程中出现了时间停留现象Fig.8 Snapshots of different times in the process of the rupture propagation with anti-asperity.Rupture halted for a while in the process of rupture propagation

3 讨论

断层自发破裂过程的数值模拟，是个高度非线性的数学问题，其解是否稳定收敛，直接决定着最终结论的正确性.因此，研究中对上述所有有限元模型的网格进行了进一步细化，然后再经过有限元计算，通过反复考察发现，加密网格后的模拟结果与原先的解基本上一致，这样就保证了文中的模拟结果是稳定可靠的.

研究中发现，地球自由表面确实在超剪切破裂的转化中发挥着重要作用，一直受到非常广泛的重视(如：Olsen et al.,1997;Aagaard et al.,2001;Zhang and Chen,2006;Kaneko and Lapusta,2010;Xu et al.,2015;Hu et al.,2019,2020).但是，即使是在整个断层面上的摩擦关系都是滑移弱化的情况下，只是降低初始应力的水平(如让S=3.0)，让所有其他的模型参数都与模型1中的一致，但是模拟结果显示，这时也不会产生二次破裂，即不会产生超剪切破裂现象(见图9所示).所以，要产生超剪切破裂地震，除了地表附近的摩擦强化层厚度薄(或没有)以外，初始应力水平也要足够的高.

图9 在低初始应力状态下(S=3.0)，破裂传播过程中不同时刻的快照.图中所见，尽管存在如模型1中的地球自由表面(其他模型参数与模型1完全一致)，但由于应力水平的降低，破裂过程中不出现二次破裂，更没有出现马赫波，所以在此情况下，破裂的平均速度只有2754 m·s-1，不会产生超剪切破裂现象Fig.9 Snapshots of rupture propagation at different times in the case of low initial stresses (S=3.0).Although the Earth′s free surface is existent as in Model 1,with all other model parameters kept the same as in Model 1,no secondary rupture or Mach waves were observed in this case in which no supershear rupture is seen with the average rupture speed of 2754 m·s-1,due to low initial stresses

断层破裂越过断层阶区、障碍体及反凹凸体时，破裂过程中出现时间上的短暂停顿，是由于破裂越过这些障碍时需要更高的破裂能，因此需要一定的时间来积累能量.这样尽管有可能在局部的断层段上出现了超剪切破裂，但整个破裂过程中的平均破裂传播速度就有可能显著地低于剪切波的速度，这样我们就很难捕捉超剪切地震的发生.这也是自然界中超剪切破裂地震数量少的一个重要原因.

综合前人的研究，我们发现若要产生目前可以识别的超剪切破裂地震，需要断层几何形状比较简单，在空间上不间断、连续、断层平直，并且断层长度要足够长，此外初始应力场分布均匀且应力水平较高(Xia,et al.,2004；Das,2007;Robinson et al.,2010;Bouchon et al.,2010;Mello et al.,2010)；另外还要有比较密集的地震观测台站，获取足够多有效的信号，才能够进行有效地辨别超剪切破裂地震.这些苛刻的条件导致了我们平常看到的超剪切破裂地震在自然界中数量很少.

或许自然界中的超剪切破裂地震数量并不很少，只是我们目前没有 “看到”.另外一种可能是，在一次地震事件中，由于断层几何、介质属性、应力状态、摩擦关系等在空间的分布都是不均匀的，超剪切破裂有可能在断层的局部区段出现.如：2008年汶川大地震，总体来说这是一次亚剪切地震破裂事件，但在北川地区却出现了超剪切破裂(如：杜海林等，2009；Wang et al.,2016)，使得北川地区的地震灾害最为严重(朱守彪和袁杰，2018).随着观测台站的加密，观测手段的提高，观测技术的完善，地震分析技术的不断改进，可能今后会发现越来越多的超剪切破裂地震.但究竟自然界中有多少超剪切破裂的地震，震级分布范围怎样？其数量与亚剪切破裂地震的数量之间有没有“某种”定量关系，都是今后需要深入研究的问题.

4 结论

研究中利用有限单元方法计算了当地球自由表面存在一个2 km厚的速度强化的摩擦关系的薄层介质时对产生超剪切破裂的影响；此外还模拟了断层上的障碍体、反凹凸体以及断层阶区对于断层自发破裂传播过程的作用及破裂传播速度转换的详细过程，主要结论具体如下：

有限单元方法在模拟断层因摩擦失稳导致的自发破裂这个高度非线性问题方面，具有良好的优势，计算过程稳定、结果收敛可靠，随着超级计算设备的普及，该方法可以用来定量研究很多地质、地震等科学问题.

尽管地球自由表面在触发产生超剪切破裂方面效率很高，但当地表附近存在沉积层、未固结的断层泥等松软介质时，地表附近断层介质是速度强化的摩擦本构关系，此时亚剪切破裂无法有效地转换为超剪切破裂，近地表的这层摩擦速度强化层会严重抑制超剪切破裂的发生；这是我们看到自然界中超剪切破裂地震很少的一个重要原因.

其次，断层上的障碍体、反凹凸体、断层阶区等虽然可以促进亚剪切破裂转换为超剪切破裂，但在转化的过程中，由于出现了破裂暂停，这样整个断层上的平均破裂速度就成为亚剪切破裂速度，因此就很难辨别这种局部的超剪切破裂事件.若要产生一个目前可以识别的超剪切破裂地震，其条件非常苛刻，通常断层的长度要足够的长，断层几何要足够平直，初始应力水平要足够高，地表的摩擦速度强化层厚度要足够薄，近场要有足够多的地震台站，等.这样，总体来看我们能够看到的超剪切破裂地震事件就非常稀少.本研究除了对为什么自然界中超剪切破裂地震稀少这一科学问题进行了初步解释外，同时也加深了我们对震源动力学、断层破裂习性及地震灾害评估的认识.

致谢王仁先生的学术思想对作者的研究工作影响深远.北京大学蔡永恩教授对本研究有诸多指导，三位匿名审稿专家提出了许多意见和建议，在此表示感谢.