一种基于消息传递的时域重叠复用译码算法*

胡峰华，王亚峰，金 婧

（1.北京邮电大学，北京 100876；2.中国移动研究院，北京 100032）

0 引言

随着移动通信业务的迅速发展，无线频谱资源越发的短缺[1]，这极大程度上限制了未来移动通信技术的发展。因此，如何实现高频谱效率和提高信号的传输速率，是未来移动通信技术研究的重要方向。李道本教授通过多年的理论研究，提出了一种高频谱效率的编码方式，称为重叠X 域复用编码[2-4]，它包含时域重叠复用（Overlapped Time Division Multiplexing，OvTDM）、频域重叠复用（Overlapped Frequency Division Multiplexing，OvFDM）以及码域重叠复用（Overlapped Code Division Multiplexing，OvCDM）。尽管这种编码方式很大程度上提升了系统的传输速率，但是由于引入了符号间的干扰，因此这种编码方式在译码时运算复杂度很高，很难应用于实际。目前OvTDM 系统常用的译码算法有维特比算法[5]、Fano 算法[6]、stack 算法[7]等。其中，维特比算法具有最佳的译码性能，但是译码复杂度随重叠复用系数的增大呈指数增加，在高重叠复用系数的情况下是难以接受的；Fano 算法和stack 算法虽然在运算复杂度方面相比于维特比算法有所降低，但是它们的译码性能相比维特比算法有着很大的差距。在这样的背景下，如果能研究出一种低运算复杂度高性能的OvTDM 系统译码算法，就能推动OvTDM 编码方式在实际生产中的应用。因此本文研究了OvTDM 系统的卷积编码方式，发现该系统在发送序列和接收信号之间存在特殊的对应关系，以此为基础能构建出关联程度很大的因子图结构。在此基础上，本文将消息传递的思路应用到OvTDM 系统的译码过程中提出了一种新型的OvTDM 系统译码算法[8-11]，在实现低运算复杂度的同时有着较好的译码性能。

1 系统模型

相比于无符号间干扰的正交奈奎斯特系统，OvTDM 系统中存在波形的重叠，人为引入了符号间干扰，而重叠复用原理指出这种干扰是一种编码约束关系，波形重叠得越严重，系统获得的增益反而越高。OvTDM 系统本质上是复用波形在时域上的移位叠加，图1 给出了OvTDM信号的编码过程。

图1 重叠复用系数为3的OvTDM 系统信号编码过程

如图1 所示为一个重叠复用系数为3的OvTDM系统信号的编码过程，可以看出OvTDM信号的产生是通过时域复用波形的移位和叠加所产生的。这里g(t)代表周期为T的时域复用波形，K表示重叠复用系数，则每次移位的间隔为T/K。从图1 中不难看出相邻的K个符号之间是存在干扰的，这种干扰是人为引入的，但是这种干扰与信道噪声不同，它是符号之间的一种编码约束关系。当重叠复用系数越大时，波形重叠得越紧密，系统单位时间携带的符号信息也越多，OvTDM 系统以此来实现高编码增益。虽然这种方式实现了高编码增益，但是因为人为引入了符号间干扰，接收端信号的译码过程变得更加的困难，极大地增加了运算复杂度。

图2 给出了加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道环境下OvTDM 系统从信号产生到接收端译码的总流程。

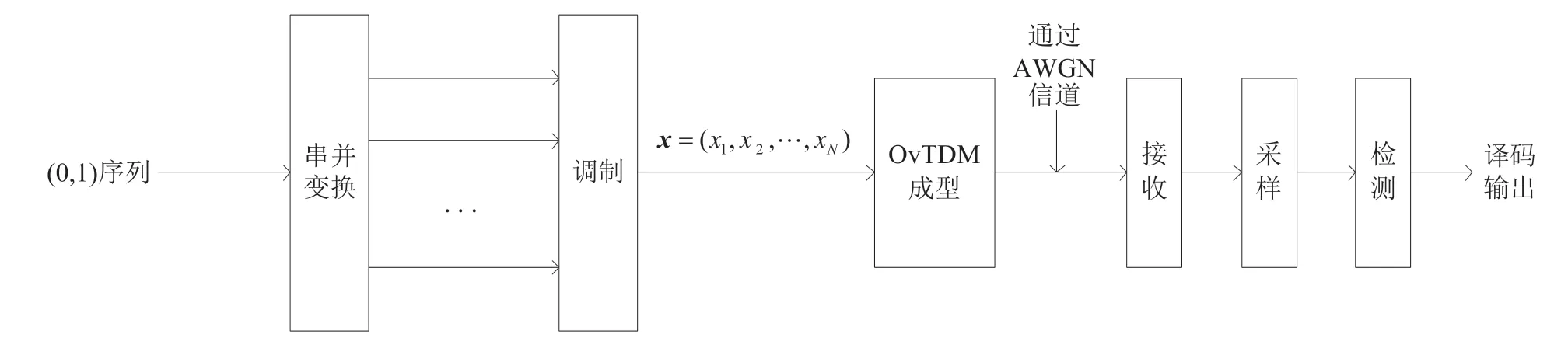
图2 AWGN信道下OvTDM 系统流程

如图2 所示，假定发送序列是等概率发送的无记忆信源，待发送的0、1 序列经过串并变换和调制后映射为调制序列x。调制序列进入OvTDM 成型滤波器后，经过复用波形的移位与叠加之后产生了OvTDM信号，该信号经过AWGN信道进行信号的传输。信号到达接收端后，与传统的传输系统不同，它无需进行匹配滤波，而是直接进行采样和译码，最终得到译码输出的序列，这就是OvTDM信号从产生到译码的总过程。这里假设长度为N的待发送的调制符号序列为x，设定OvTDM 系统采用的复用波形为g(t)(t∈[0,T])，g(t)表示周期为T且能量归一化的脉冲成型波形。基带OvTDM信号s(t)可以表示为：

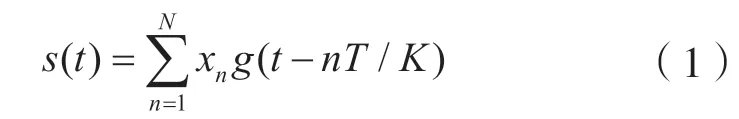
式中：xn表示第n个待发送的调制符号。

基带信号经过AWGN信道之后到达接收端，获得的接收端信号为：

式中：n(t)表示信道噪声。

然后接收信号y(t)不经过匹配滤波器，直接进行采样和译码，得到译码序列，至此流程结束。

2 算法原理

如果一个多变量的全局函数可以分解成多个局部函数乘积的形式，则可以使用因子图来描述变量与局部函数之间的关系。消息传递往往是在因子图模型的基础上进行的，用来表征因子图上各个节点之间消息进行传递更新的过程。在OvTDM 系统的接收端，每T/K周期内的接收信号都与多个发送符号有关。由于OvTDM 系统的卷积编码结构引入了数据符号间的干扰，OvTDM 系统在接收信号和发送符号之间能构建易于进行信息传递的因子图模型。在这样的情况下，本文将消息传递的思想应用于OvTDM系统的译码过程中，提出了一种基于消息传递的OvTDM 译码算法。算法的原理步骤如下文所述。

假设调制序列为：

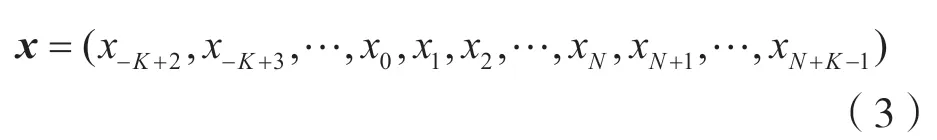
式中：(x-K+2,x-K+3,…,x0)为序列头部；(xN+1,…,xN+K-1)为序列尾部；(x1,x2,…,xN)为实际发送的符号。序列头部和序列尾部两部分为已知序列，(x1,x2,…,xN)为待检测序列。式（3）中N为发送符号数目，K为重叠复用系数，本论文采用二进制相移键控（Binary Phase Shift Keying，BPSK）调制。

假设OvTDM 系统的复用波形为：

式中：gi(t)(i=1,2,…,K)为第i个子复用波形。

设定g=(g1,g2,…,gK)是子复用波形在对应周期内的采样值。

这里假设接收序列为：

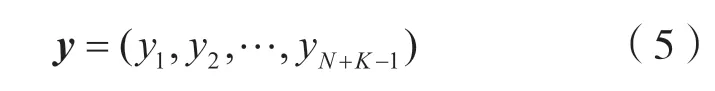
式中：yl(l=1,2,…,N+K-1)为接收信号在第周期内的采样值。

根据OvTDM 系统的卷积编码方式可知：

式中：nl为接收端噪声信号在第周期内的采样值。

进一步推导可以得出：

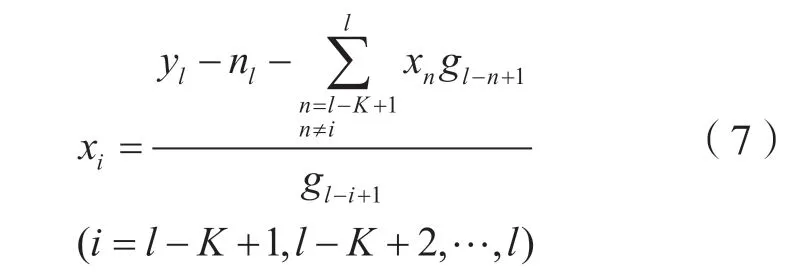
根据式（7）中发送符号和接收序列的关系，本文提出了一种基于消息传递的OvTDM译码算法，算法流程如下：

步骤一：式（7）取i=l有：

若xl的前K-1 个发送符号的估计值已知，则根据式（8）可以求出xl的估计值，即(xl-K+1,xl-K+2,…,xl-1)已知，则可以估计xl，又(x-K+2,x-K+3,…,x0)为已知符号序列。因此，根据已知的符号序列可以估计x1的值，这里记x1的估计值为E(x1)。由于本文采用BPSK 调制，则利用：

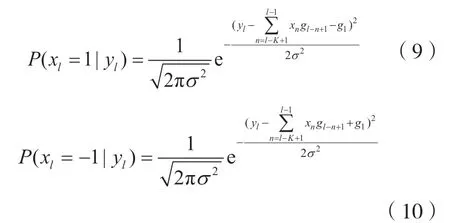
将式（9）、式（10）归一化得到：

取l=1，则可以求出x1的估计值：

计算出x1的估计值E(x1)后，这就可以作为已知条件进一步求出x2的估计值，以此类推直到求出xN的估计值E(xN)，最后将本步骤求出的所有估计值作为初始估计序列传入后续的步骤。

步骤二：本文以发送符号为变量节点，以接收序列为函数节点，依据OvTDM 系统的卷积编码结构构建了OvTDM 系统的因子图模型。重叠复用系数为3的OvTDM 系统因子图模型如图3 所示。

图3 K=2 时OvTDM 系统的因子图模型

若只看某个函数节点yl(l=1,2,…,N+K-1)，则该部分的因子图模型如图4 所示。

图4 函数节点部分的因子图模型

若只看x1到xN的某个变量节点xi(i=1,2,…,N)，则该部分的因子图模型如图5 所示。

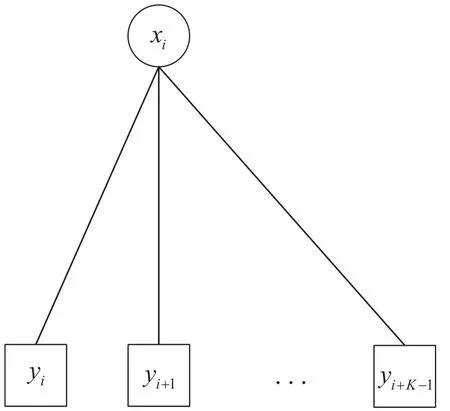
图5 变量节点部分的因子图模型

根据消息传递的原理，每一个函数节点传递给与之相连的变量节点的信息其计算公式为：

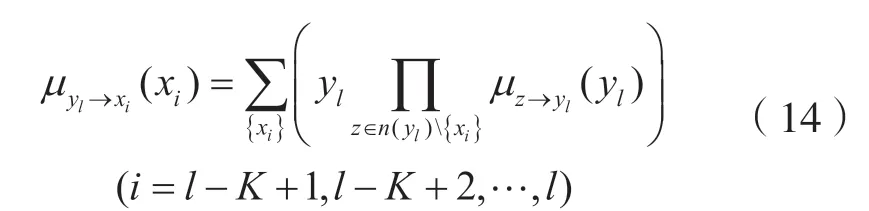
式中：n(yl)为所有与yl相关联的变量节点；z为除xi以外与yl相关联的变量节点。这里假设μyl→xi(xi)=E'(xi|yl)。因为OvTDM 系统的相邻符号之间存在干扰，所以系统接收端的噪声信号之间是存在相关性的，本文为了简便处理将接收端噪声信号假定为均值为0，方差为σ2的高斯随机变量。又因为发送序列是等概率的无记忆信源，所以调制序列x是独立同分布的0 均值高斯随机变量，基于此，本算法将式（7）中的部分进行高斯近似，这里假设近似后该部分为，则有：

由于采用的是高斯近似，所以的均值为：

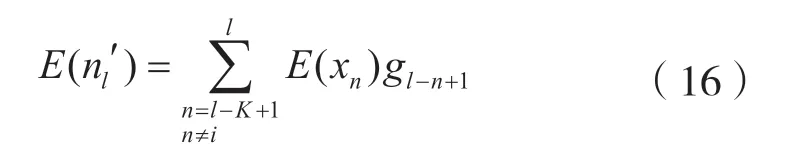
的方差的计算方式为：

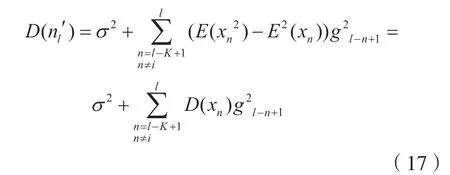
则xi是满足均值为E(xi)，方差为D(xi)的高斯随机变量，其中：

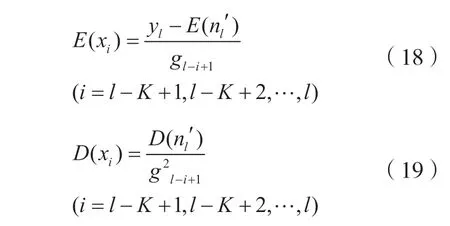
据此可以求出：

可以求出由yl传递给xi的信息为：

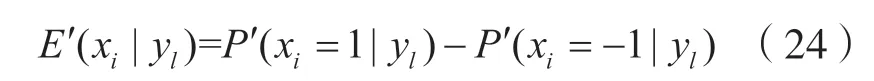
根据上述的计算方式，利用第一步中获取的传输序列的初始估计值，可以按照从y1到yN+K-1的顺序，计算每一个函数节点yl(l=1,2,…,N+K-1)向与之关联的变量节点xi(i=l-K+1,l-K+2,…,l)所传递的信息。

步骤三：根据变量节点部分的因子图结构，变量节点向与之关联的函数节点传递的信息μxi→yl由除yl外所有与xi相连的函数节点传递过来的信息决定。基于此，本文设定：

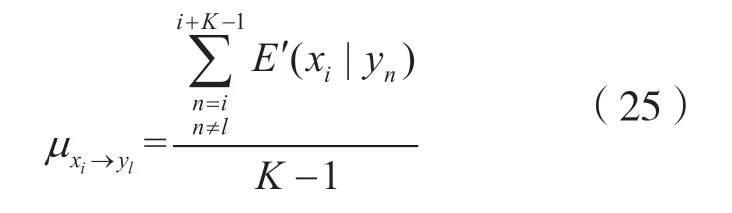
本步骤按照式（25）分别计算从x1到xN的变量节点向与之相关联的所有函数节点传递的信息，这些信息将作为新的序列估计值用于下一次迭代过程中。步骤二和步骤三，整体上为一次迭代的过程，每次迭代重复上述的过程，直到达到预设的迭代次数。

步骤四：迭代结束后按照消息传递的原理可以计算xi(i=1,2,…,N)的最终估计值为：

最后按照上述估计值进行判决，得出判决序列作为译码结果，至此译码结束。

3 算法复杂度分析

本算法的运算复杂度，主要由以下4 个部分构成。

（1）步骤一的运算复杂度，这部分与迭代次数无关，在计算初始估计值的过程中，分别计算了每个发送序列符号的两个状态的概率，因此本部分的运算复杂度为O(2N)。

（2）步骤二的运算复杂度，这部分对于每一个函数节点都计算了该函数节点向与之关联的发送符号传递的信息，每份信息都由对应发送符号的两个状态的概率组成。这部分与迭代次数有关，假设迭代次数为M，则运算复杂度为O(2NMK)。

（3）步骤三的运算复杂度，这部分对于每一个发送符号都计算了该符号向与之关联的函数节点传递的信息，这部分也与迭代次数有关，所以本部分的运算复杂度为O(NMK)。

（4）步骤四的运算复杂度，这部分与迭代次数无关，运算复杂度为O(N)。

因此本算法的总运算复杂度为O(3NMK+3N)。

表1 给出了本算法和维特比算法、Fano 算法的译码复杂度对比。

表1 算法译码复杂度对比

如表1 所示，维特比算法的译码复杂度随重叠复用系数的增大呈指数增加，因此在高重叠复用系数的条件下该算法的译码复杂度是难以接受的。而对于Fano 算法和本文所提的算法，它们的译码复杂度随着重叠复用系数的增大都是呈现线性的关系，因此在高重叠复用系数的条件下能很好地降低译码复杂度。

4 仿真结果与分析

本文按照表2 所示的仿真参数分别对维特比算法、Fano 算法和本文提出的算法进行了译码仿真。

表2 仿真参数

经过多次仿真发现，随着重叠复用系数的增加，本文提出的算法性能减少收敛所需的迭代次数。当K=2 时，本算法经过4 次迭代译码的性能基本就收敛了，所以在后面的仿真中本算法以4 次迭代为例进行仿真，仿真结果如图6、图7、图8、图9所示。

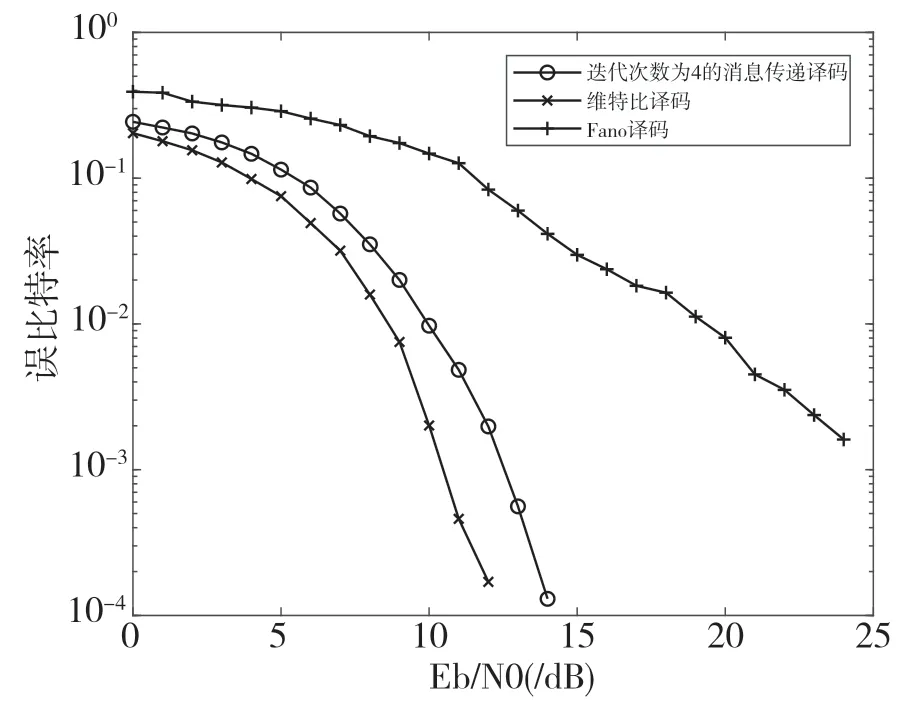
图6 K=2 时3 种译码算法性能对比

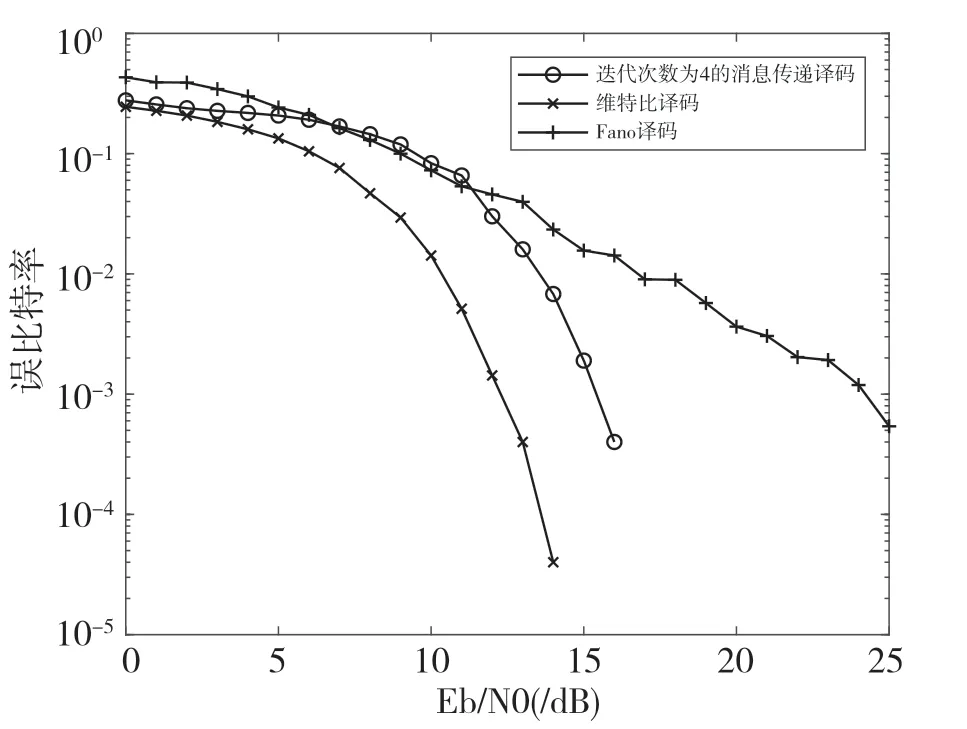
图7 K=3 时3 种译码算法性能对比

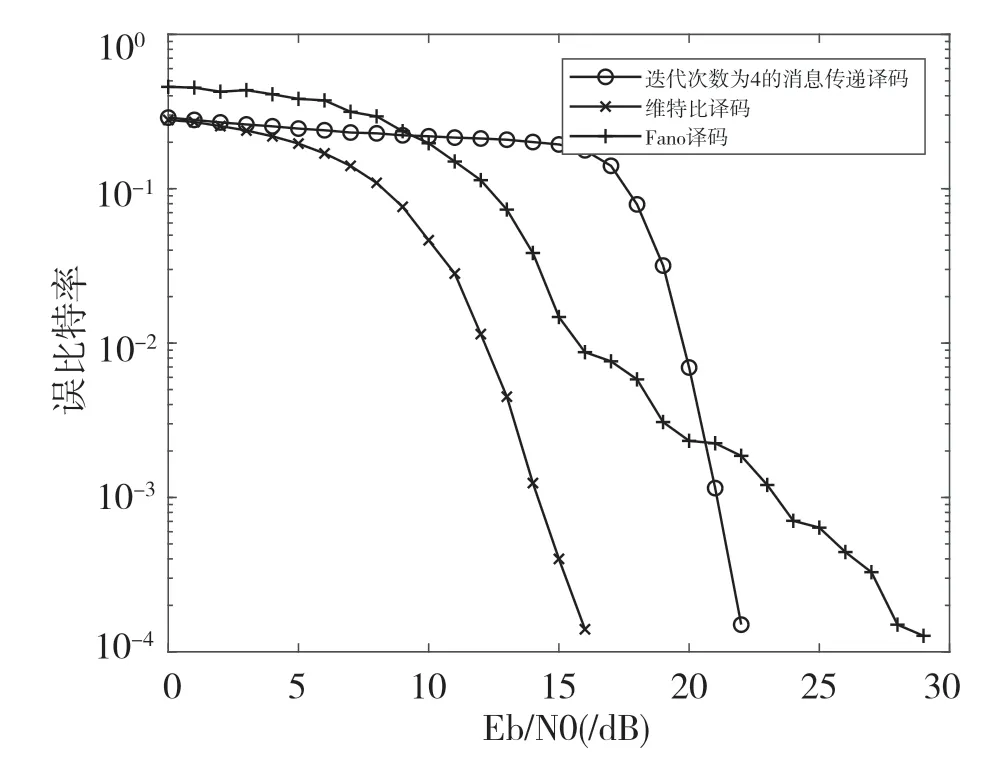
图8 K=4 时3 种译码算法性能对比

图9 K=5 时3 种译码算法性能对比

如图6、图7、图8、图9 所示，可以看出在重叠复用系数K=2,3的条件下，本文提出的算法具有良好的译码性能，其译码性能超过了Fano 算法，与维特比算法的性能接近。同时也可以发现，本算法在高信噪比的情况下其性能要好于Fano 算法，而在高重叠复用系数和低信噪比的条件下，本算法的性能不如Fano 算法。本文推测其原因是在该条件下由于噪声干扰和叠加影响导致译码状态数目多，本算法的译码检测过程只能约束在长度为K的路径内，而Fano 算法译码过程是在整个译码路径中进行的。在高信噪比情况下，噪声的干扰影响远小于叠加影响，本算法在消息传递的过程中，由于噪声干扰的减小，在计算发送序列估计值的时候能够更加地接近实际的发送序列，使得本算法的译码性能优于Fano 算法。

5 结束语

本文针对OvTDM 系统的检测问题提出了一种基于消息传递的OvTDM 系统的译码算法。在结合OvTDM信号的卷积编码方式的基础上，本算法构建了关联发送符号和接收信号的因子图模型，并在因子图的变量节点和函数节点之间实现了消息的传递更新，最终经过迭代之后进行判决译码。仿真结果表明本文提出的算法与传统的检测算法相比能实现较好的译码性能，同时具有较低的运算复杂度。因此，本文提出的基于消息传递的OvTDM 系统译码算法在OvTDM 领域是很有应用前景的。

致 谢

本研究由北京邮电大学-中国移动研究院联合创新中心资助，在此表示感谢。