两类图族的Merrifield-Simmons指标

苏晓海，孙泽清,俞天仕，高 云，任胜章

(陕西理工大学 数学与计算机科学学院，陕西 汉中 723001)

设图G(V,E)是简单的连通无向图，并且V(G)和E(G)分别是它的顶点集和边集，分别简记为V和E.称集合A为图G的一个独立集,如果A⊆V(G)，对于任意的两个顶点u,v∈A,都有uv∉E(G)成立,其中空集为任何图的一个独立集[1-8].图G的Merrifield-Simmons指标是指图G的独立集的个数，记为σ(G).图的Merrifield-Simmons指标是由Richard E.Merrifield和Howard E.Simmons两位美国化学家在1989年引入的拓扑指标[7-9].Merrifield-Simmons指标在化学图论中具有非常重要的作用,该指标与烷烃的物理化学性质尤其是与物质的沸点有着密切联系，且在有机化合物的合成和新药物的研发领域有着较为广泛的应用.

设e为图G的一条边,x为图G的一个顶点,将图G删去一条边e后得到的图记为G-e,图G删去一个顶点x及其关联的所有边后得到的图记为G-x.在论文中没有给出的术语和记号可参见文献[17].

论文中将Fibonacci数简记为Fn,满足Fn=Fn-1+Fn-2,n≥2,且F0=0,F1=1.Cn表示含有n个顶点的圈；Kn表示n阶完全图；G(Pm,Kn)是由一条m个顶点的路的每个顶点上粘接一个n阶完全图Kn得到的连通图，称之为路粘完全图(图1)；G(Cm,Kn)表示由圈Cm的每个顶点上粘接一个n阶完全图Kn得到的图，称之为圈粘完全图(图4).论文主要研究路粘完全图G(Pm,Kn)和圈粘完全图G(Cm,Kn)的Merrifield-Simmons指标，并分别给出了其Merrifield-Simmons指标的计算公式.

1 相关引理

引理1[1]设G是一个简单的连通图,对∀uv∈E(G),u∈V(G),令NG[u]={v|uv∈E(G)},则

σ(G)=σ(G-u)+σ(G-NG[u]).

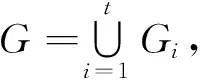
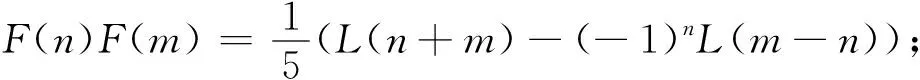
(3)F(m)L(n)=F(n+m)-(-1)mF(n-m)=F(m+n)+(-1)nF(m-n).

引理4[1]设Pn为n阶的路,Cn为n阶的圈，则：

(1)σ(Pn)=Fn+2；

(2)σ(Cn)=Fn+1+Fn-1.

引理5[4]设实数组q1,q2,…,qt是常系数齐次递推关系式H(n)=a1H(n-1)+a2H(n-2)+…+akH(n-k)的特征方程的所有互不相等的特征根,并且它们的重数依次为e1,e2,…,et,则递推关系对应于qi部分的解为Hi(n)=(c1+c2n+…+ceinei-1)qin,而递推关系式的一般解为

H(n)=H1(n)+H2(n)+…+Ht(n).

2 主要结论及证明

定理1设图G是n个顶点的完全图，则

σ(Kn)=n+1.

证明已知σ(Ø)=1,由引理1，有

σ(Kn)=σ(Kn-u)+σ(Kn-NG[u])=σ(Kn-1)+σ(Ø)=

σ(Kn-1)+1=σ(Kn-2)+σ(Ø)+1=…=

σ(K3)+n-3=4+n-3=n+1.

定理2设图G(Pm,Kn)是m×n个顶点的路粘完全图，则

证明图G(Pm,Kn)(图1)去掉一个顶点vn得到的图为G(Pm,Kn)-vn(图2)，而图G(Pm,Kn)-vn再去掉一个顶点vn-1得到的图为G(Pm,Kn)-vn-vn-1(图3).

图1 路粘完全图G(Pm,Kn)

图2 图G(Pm,Kn)-vn

图3 图G(Pm,Kn)-vn-vn-1

由引理1，2，得

σ[G(Pm,Kn)]=σ[G(Pm,Kn)-vn]+σ[G(Pm,Kn)-NG[vn]]=

σ[(Kn-1)G(Pm-1,Kn)]+σ[(Kn-1)G(Pm-2,Kn)]=

nσ[G(Pm-1,Kn)]+nσ[G(Pm-2,Kn)]，

即

σ[G(Pm,Kn)]=nσ[G(Pm-1,Kn)]+nσ[G(Pm-2,Kn)].

(1)

由于(1)式是关于m的递推关系,所以由引理5可得其特征方程为x2-nx-n=0,对应的特征根为

所以递推关系(1)的通解为

(2)

利用引理1，2，可以计算得递推关系(1)的初始值为

σ[G(P2,Kn)]=n(n+1)+n=n2+2n,

σ[G(P3,Kn)]=nσ[G(P2,Kn)]+n(n+1)=n(n2+2n)+n2+n=n3+3n2+n.

把初始值代入(2)式得到以A,B为未知参数的方程组为

(3)

解方程组(3)，得

(4)

再将(4)式代入(2)式，得

证毕.

定理3设图G(Cm,Kn)是m×n个顶点的圈粘完全图，则

证明圈粘完全图G(Cm,Kn)(图4)去掉一顶点vn得到图G(Cm,Kn)-vn(图2)，图G(Cm,Kn)-vn去掉一顶点v1得到图G(Cm,Kn)-vn-vn-1(图5).

图4 圈粘完全图G(Cm,Kn)

图5 图G(Cm,Kn)-vn

由引理1，2，得

σ[G(Cm,Kn)]=σ(G-vn)+σ(G-NG[vn])=σ(kn-1G(Pm-1,Kn))+σ(kn-1G(Pm-3,Kn)kn-1)=

nσ[G(Pm-1,Kn)]+n2σ[G(Pm-3,Kn)]，

即

σ[G(Cm,Kn)]=nσ[G(Pm-1,Kn)]+n2σ[G(Pm-3,Kn)].

(5)

再利用定理2的结论，得

3 结束语

首先应用常系数齐次递推关系式的性质得出n阶完全图Kn的Merrifield-Simmons指标计算公式；其次利用n阶完全图Kn的Merrifield-Simmons指标计算公式，应用常系数齐次递推关系式的性质得出了路粘完全图G(Pm,Kn)的Merrifield-Simmons指标的计算公式；最后通过应用定理1,2的结论得出圈粘完全图G(Cm,Kn)的Merrifield-Simmons指标的计算公式.