基于改进蚁群算法的柑橘采摘最优路径

陈 鑫，王海宝*，罗 强，王昌洪，钱 伟

(1.重庆三峡学院 智能山地农机技术研究中心，重庆 404120；2.中国科学院 合肥智能机械研究所，安徽 合肥 230031)

随着自动控制技术的推广，智慧农业[1-2]得到快速发展.柑橘多数生长在山区，山地地貌使柑橘采摘消耗大量的人力、物力，且采摘效率极其低下.路径规划[3-4]已应用于智慧农业.文献[5]对农田环境下机器人的运行路径进行了优化.文献[6]设计及实现了植保无人机按规划航迹播撒种子的方案.文献[7]解决了无人机在喷洒过程中的重喷漏喷问题.文献[8]解决了切割工艺中路径规划能耗大的问题.

路径规划算法可分为：传统经典算法[9]、现代智能算法[10].传统经典算法有：Dijkstra算法、人工势场法及模拟退火法[11].传统经典算法应用于3维空间果实采摘时，存在计算量大、收敛速度慢、易陷入局部最优解等问题[12].现代智能算法中的蚁群算法具有分布计算、群体智能、正反馈、鲁棒性强等优点，解决了不少3维路径规划问题[13-15].然而，蚁群算法受信息素分布及挥发的影响，前期搜索解空间时，易陷入局部最优解[16-17].基于此，笔者引入信息素浓度的更新机制，提出一种改进蚁群算法，以加快算法收敛速度，避免陷入局部最优解，得到柑橘采摘的最优路径.

1 柑橘采摘的数学模型

在柑橘采摘过程中，认为柑橘相对于果树静止，将柑橘采摘的路径规划抽象为旅行商问题[18]的解集.将柑橘果实点视为旅行商问题中的城市点，根据1棵柑橘果树的平均大小，柑橘采摘的最优路径为1个约为10 m×10 m×10 m的3维空间中旅行商问题的最优解.

设赋权图G=(V,E)，其中V为顶点集，E为路径的权值或长度集合.

定义

(1)

其中：i,j为相邻果实点.

经典的旅行商问题的数学模型为

(2)

使得

(3)

其中：dij为相邻果实点的距离，S为顶点集V中所有非空子集，|S|为集合S在赋权图G中的顶点数.

式(3)～(4)能保证每个点仅有一条边进和一条边出，式(5)能保证该模型没有子回路解.

2 改进的蚁群算法

2.1 蚁群算法

蚁群算法是一种仿生启发式算法[19-20].自然环境下，蚂蚁寻找食物时分泌一种独特的化学物质，这种物质被称作信息素.在特定范围内，蚂蚁能感知信息素的存在，蚂蚁就爬向信息素浓度高的地点.随着时间的累积，蚂蚁数量不断增多，该路径上堆积的信息素浓度就增大，使蚂蚁选择该路径的概率增大.最终，整个蚂蚁群体在信息素浓度的正反馈机制[21]作用下，寻得最优路径.

设在3维空间中有n个柑橘，柑橘i到柑橘j的距离为

(4)

其中：(xi,yi,zi)为柑橘i在3维空间中的坐标；(xj,yj,zj)为柑橘j在3维空间中的坐标.

蚂蚁W从柑橘i到柑橘j的状态转移概率为

(5)

信息素浓度以如下方式更新

τij(t+1)=(1-ρ)τij(t)+Δτij,0<ρ<1，

(6)

信息素释放机制模型有以下3种：蚁周模型、蚁量模型及蚁密模型.

(7)

其中：Q为蚂蚁k释放信息素浓度总量，Lk为蚂蚁k经过的从柑橘i到柑橘j的路径长度.

(8)

Δτij=Q.

(9)

2.2 改进的蚁群算法

在蚁群算法中，蚂蚁每次选择目标点路径时，趋向于优先选择最优路径.当目标点增多的时候，由于信息素随时间挥发的程度不均匀，某些路径信息素挥发过快，导致蚂蚁在选择下一路径时不能选择最优路径，算法会在局部最优解的领域停滞，降低了全局搜索解空间的能力，为此提出一种改进的蚁群算法.

为了避免陷入局部最优解，引入如下的随时间改变的自适应信息素浓度更新机制

(10)

其中：Lmin为柑橘i到柑橘j的路径长度最小值，Lmax为柑橘i到柑橘j的路径长度最大值，γmax为柑橘i到柑橘j的最大路径因子，γmin为柑橘i到柑橘j的最小路径因子.

改进的信息素浓度更新机制，避免了在解空间连续域出现间断点，自适应改变信息素挥发的程度，使信息素浓度更均匀，得到更多的解空间，提高了全局搜索解空间的能力.

改进的蚁群算法流程如图1所示.

图1 改进的蚁群算法流程图

3 仿真实验

为了验证改进蚁群算法的有效性与可行性，在window10操作系统下通过IntelliJ IDEA2020.1，JDK1.8进行仿真实验.柑橘果实以质点表示，根据柑橘果实点的坐标，在3维坐标系中绘图.图2为3维坐标系中柑橘果实点.

图2 3维坐标系中柑橘果实点

3.1 参数优化

参数设置如表1所示.只改变1个参数而其他参数不变时，进行比较实验.综合分析笔者进行的大量比较实验及有关文献实验结果[22-23]可知，当α=3、β=4、ρ=0.2、γmax=10、γmin=0.5、Q=20、蚂蚁数量为柑橘果实点数量的1.5倍时，改进蚁群算法可得到最优路径.

表1 参数设置

3.2 实验结果

3.2.1 2种算法比较

在进行对比试验前，按上述优化参数对蚁群算法及改进蚁群算法进行设置.柑橘果实数量为31时的2种算法的采摘路径如图3所示.柑橘果实数量为144时的2种算法的采摘路径如图4所示.由图3可知：改进蚁群算法的路径长度比蚁群算法的路径长度短；在果实点较密集区域，蚁群算法已陷入局部最优解，改进蚁群算法则没有陷入局部最优解.分析图4可以得到与图3相同的结论，可见该结论与柑橘果实数量无关.

图3 柑橘果实数量为31时的2种算法的采摘路径

图4 柑橘果实数量为144时的2种算法的采摘路径

表2为2种算法的路径长度及其对比.由表2可知，不管柑橘果实数量如何变化，改进蚁群算法路径长度均比蚁群算法路径长度短.

表2 2种算法的路径长度及其对比

改进蚁群算法的路径长度比蚁群算法的路径长度短的原因为：在果实繁密的情况下，蚁群算法释放的信息素浓度不均匀，易陷入局部最优解；而改进蚁群算法引入了随时间改变的自适应信息素浓度更新机制，不会陷入局部最优解.因此，改机蚁群算法的性能比蚁群算法更优.

3.2.2 3种模型比较

图5为改进蚁群算法采用3种模型的采摘路径.由图5可知，在3种模型中，蚁周模型的路径长度最短.

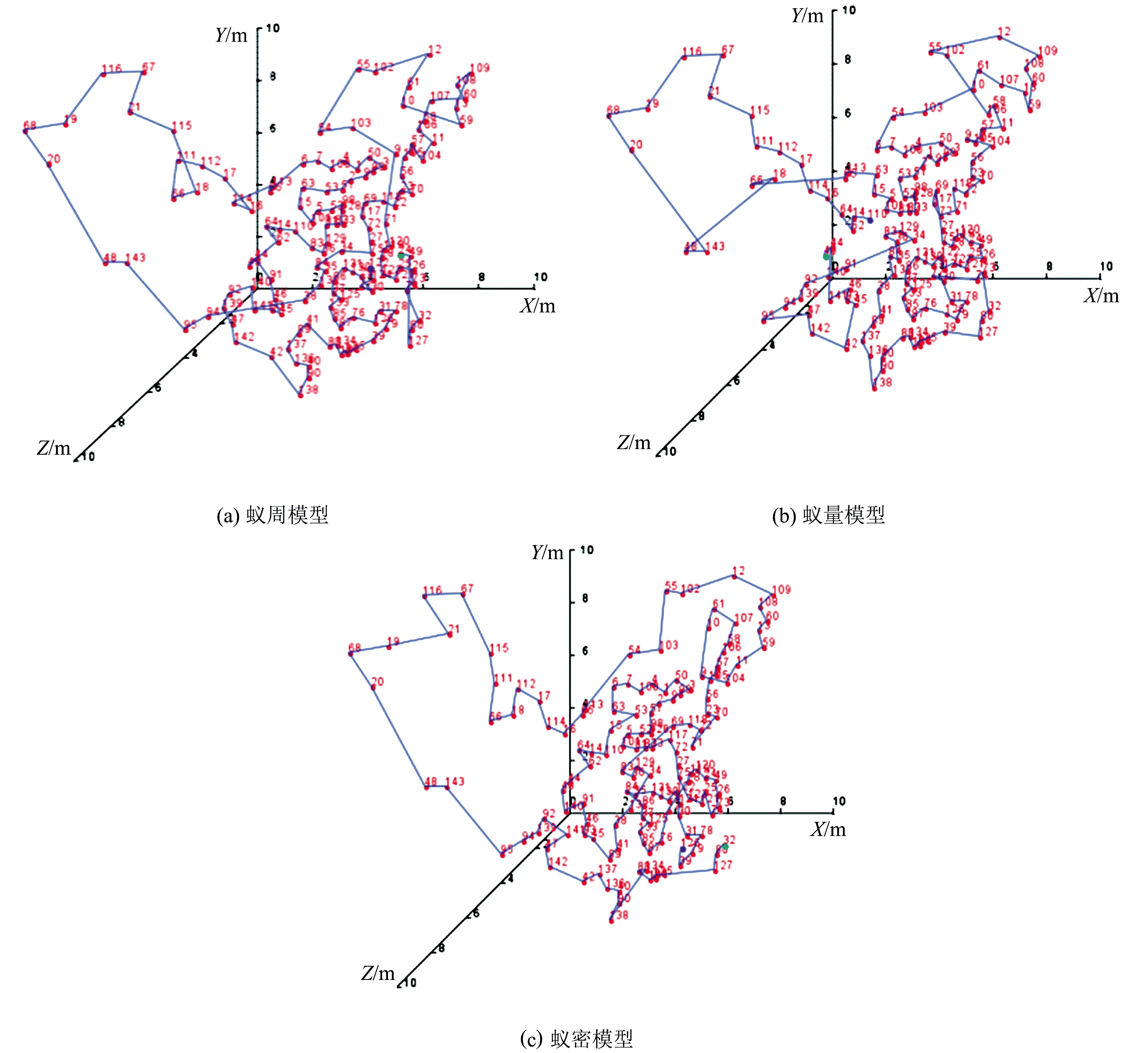
图5 改进蚁群算法采用3种模型的采摘路径

表3为改进蚁群算法采用3种模型的路径长度及其对比.由表3可知，不管柑橘果实数量如何变化，蚁周模型的路径长度均比蚁量模型和蚁密模型的路径长度短.蚁周模型为最优模型的原因为：蚁量模型和蚁密模型更新信息素时，选择的是局部信息素，而蚁周模型选择的是全局信息素，不易陷入局部最优解.因此，改进算法应该采用蚁周模型.

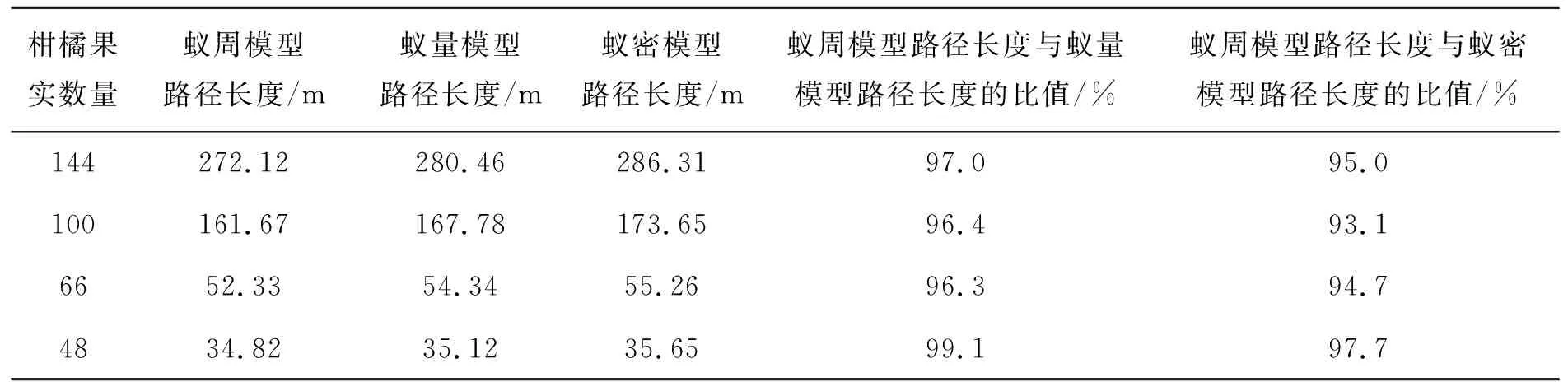
表3 改进蚁群算法采用3种模型的路径长度及其对比

4 结束语

笔者将柑橘采摘的路径规划抽象为旅行商问题的解集，提出了改进蚁群算法，该算法引入了随时间改变的自适应信息素浓度更新机制.仿真实验结果表明：改进蚁群算法的路径长度比蚁群算法的路径长度短；相对于蚁量模型和蚁密模型，蚁周模型为最优模型，因此改进算法应该采用蚁周模型进行路径规划.