Distributed Control of Nonholonomic Robots Without Global Position Measurements Subject to Unknown Slippage Constraints

Hao Zhang, Jianwen Sun, and Zhuping Wang

Abstract—This paper studies the fully distributed formation control problem of multi-robot systems without global position measurements subject to unknown longitudinal slippage constraints.It is difficult for robots to obtain accurate and stable global position information in many cases,such as when indoors,tunnels and any other environments where GPS (global positioning system) is denied,thus it is meaningful to overcome the dependence on global position information.Additionally,unknown slippage,which is hard to avoid for wheeled robots due to the existence of ice,sand,or muddy roads,can not only affect the control performance of wheeled robot,but also limits the application scene of wheeled mobile robots.To solve both problems,a fully distributed finite time state observer which does not require any global position information is proposed,such that each follower robot can estimate the leader’s states within finite time.The distributed adaptive controllers are further designed for each follower robot such that the desired formation can be achieved while overcoming the effect of unknown slippage.Finally,the effectiveness of the proposed observer and control laws are verified by simulation results.

I.INTRODUCTION

IN recent years, there has been great development in cooperative control of multi-agent systems [1]–[5].Compared with single agent, multi-agent systems have many advantages, such as better work efficiency, wider detection range, stronger load capacity, robustness, etc.Among these studies, more and more researchers have shown greater interest in formation control of multi-robot systems due to their potential applications, such as exploration, cooperative transportation, in search and rescue operations[6]–[8], etc.The objective of formation control for multi-robot systems is to make a group of robots move towards maintaining a desired geometric structure and overcoming disturbances from the environment.There are many methods to achieve formation control of multi-robot systems, such as leader-follower approach [9]–[12], artificial potential approach [13], virtual structure approach [14]–[15], behavior-based approach[16]–[17], etc.

The most widely adopted leader-follower formation structure is usually made up of one leader robot and multiple follower robots, in which all follower robots need to follow the leader robot while maintaining an expected geometric structure relative to the leader robot and overcoming any disturbances in the environment.In [18], a nonlinear model predictive control method based on neural-dynamic optimization was proposed for formation control of multirobot systems, where a separation-bearing-orientation scheme was designed for regular leader-follower formation and a separation-distance scheme was designed for obstacle avoidance.In [19], an adaptive PID formation control strategy was proposed to solve the formation control problem of wheeled mobile robots without knowing the leader robot’s velocity information in the leader-follower framework, which improves the robustness of formation system.In [20], a robust controller was designed for leader-follower formation by using the Lyapunov redesign technique, where the proposed controller can make the closed-loop system robust to the uncertainty associated with the state of leader robot.Nevertheless, in these papers, it is assumed that the state information of leader robot is accessible to all follower robots.When the number of robots in the system becomes large, the leader needs to communicate with all the followers; thus, the communication burden of the leader will be heavy.With the limitation of the measurement range and communication conditions in some environments, only a part of the followers can obtain the states of the leader while others can not.

Recently, many works have studied distributed formation control of multi-robot systems in order to solve the problem mentioned above.In [21], a distributed formation controller subject to velocity constraints was proposed for multiple vehicles, and the leader-follower formation was achieved without using global position measurements.In [22], a novel distributed event-triggered control strategy was proposed for multi-robot systems under fixed topology and switching topology.By using the event triggering mechanism,communication requirements and energy consumption of the whole system can be effectively reduced.In [23], the distributed event-triggered control scheme and self-triggered control scheme were developed.In [24], a distributed formation method was also proposed for switching topology.In [25], a distributed finite-time observer was designed for each follower robot such that they can get the leader robot’s states in finite time.Based on the finite-time observer, a distributed finite-time formation controller was further proposed.In [26], a distributed fixed-time controller was designed to solve the consensus tracking problem of multiple agents in the form of second-order dynamics, and the result was further extended to formation control of multi-robot systems by using linear feedback technique.The authors in[27] studied the fixed-time fuzzy adaptive bipartite containment quantized control problem for nonlinear multiagent systems subject to unknown external disturbances and unknown Bouc-Wen hysteresis.In [28], a reinforcement learning algorithm was adopted to investigate the adaptive fault-tolerant tracking control problem for a class of discretetime multi-agent systems.These works have made great contributions to distributed formation control of wheeled mobile robots.However, the proposed controllers in these papers can not be directly applied to the environments with slippage constraints.

As stated in [29], slippage is hard to avoid due to the possible existence of ice, sand, or muddy roads, which may lead to insufficient friction in the actual working environment of wheeled mobile robots.The existence of unknown slippage not only affects the control performance of conventional controllers, but also limits the application scene of wheeled mobile robots, bringing huge losses to users.So it is necessary to consider the effect of slippage when studying formation control of multi-robot systems.Till now, few works have considered the slippage constraints in formation control of multi-robot systems.In [30], formation control of wheeled robots with slippage constraints were studied for the first time,and a slip-sensitive controller was proposed such that the formation can be stabilized when slippage exists.In [31], an adaptive formation control law was proposed for wheeled mobile robots in the presence of lateral slip and parametric uncertainties.In [32], dynamic surface design method and virtual structure approach were combined to realized formation maintenance, and an adaptive technique was used to compensate for the unknown slippage.However, these papers are all based on a centralized framework, which means the states of leader robot are accessible to all follower robots.Therefore, as mentioned in the second paragraph, it is necessary to study the distributed method to overcome the effect of unknown slippage in formation control.

In addition, in most of the research results about formation control, global position information (x,y) is required for each robot in the system.However, it is difficult, and sometimes even impossible, for robots to obtain accurate and stable global position information.Therefore, it is better to use relative position and one can obtain accurate and stable relative position between different robots by using equipment such as laser radars and gyroscopes.

Followers can not access the leader’s states directly in the distributed control of leader-follower formation structure in the most of the current research.It is difficult to use the consensus-based distributed method to achieve adaptive formation control under the constrains of the existence of unknown slippage and the unavailability of global position information.Therefore, this paper adopts observer-based distributed formation control method to overcome the two constraints simultaneously.In [21], [25], [29], and [33], the observer-based method was adopted without considering the convergence rate.Compared with asymptotic convergence,finite time convergence is more conducive to formation control.However, none of the observers in [21], [29], and [33]are convergent in finite time.The observer in [25] was convergent in finite time, however, the global position information was needed for each robot.

In this paper, observer-based fully distributed adaptive control of multi-robot systems with only relative position information subject to unknown slippage constraint are studied.Firstly, a novel distributed finite time state observer without using any global position information is proposed.Compared with existing finite time observers, such as [25] and[29], this paper only needs to use the relative position information between robotRiand its neighbors to estimate the position errors relative to the leader in finite time.Secondly,based on the finite time observer, novel distributed adaptive formation controllers are further proposed without using global coordinate information and the effect of unknown slippage can be overcome.In order to deal with larger slippage, just as [34], [35] did, “slipping ratio” is adopted to model the unknown sliding disturbance, and a novel adaptive law is further designed to estimate the unknown slipping ratios.Note that a gyroscope is used for each robot to establish a common reference direction.

The major contributions of this paper can be summarized as:The fully distributed formation control of multi-robot systems without global position information while overcoming the effect of the unknown slippage constraint is proposed.Novel adaptive formation controllers and adaptive laws are proposed in the paper to achieve distributed control under the unknown slippage constraint.At the same time, in order to overcome the dependence on global position information and simplify the adaptive controllers, a novel distributed finite time state observer without using any global position information is proposed to obtain the related states of the leader.

This paper is organized as follows.Section II presents the problem formulation.In Section III, a novel distributed finite time observer and distributed formation controllers are proposed, and a strict stability analysis is given.Section IV shows simulation results of the proposed observers and controllers, which is followed by the conclusion in Section V.

II.PROBLEM STATEMENT

Consider a group ofN+1 wheeled mobile robots, labelled asR0,R1,...,RN.The kinematic model of robotRiis shown as Fig.1, where [xi,yi]Tis the position of robotRi(i∈{0,1,...,N}), θiis the heading angle of robotRi(0 ≤θi<2π), νiand ωiare the linear velocity and angular velocity.u1iandu2iare actual control inputs of robotRi, which denote the control inputs of the left and right wheels, respectively.The radius of each driving wheel of robotRiisr, and the distance between the centers of two driving wheels of robotRiis 2R.The kinematic model of robotRiis described by

Fig.1.Kinematic model of wheeled mobile robot.

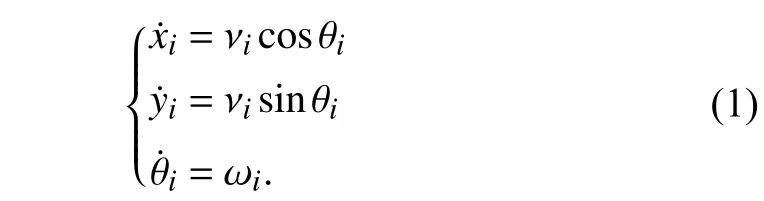
For the group ofN+1 robots, robotR0is the leader and the other robots are the followers, and all follower robots must follow the leader robot’s motion while surrounding the leader with a desired geometric structure.In this paper, it is considered that self-localization information is not available for each robot, so it is assumed that the leader robot can carry out local path planning autonomously by SLAM(simultaneous localization and mapping) or other technology,and the leader robot has the ability to overcome the unknown slippage from the ground.The design of the leader’s controller can refer to the follower robots’ controllers in the following chapters.In addition, consider the actual situation, the input states of the leader robotR0should satisfy the following assumptions.

Assumption 1:ν0(t), ω0(t),(t),(t),x0(t),y0(t) and θ0(t)of the leader robotR0are all continuous and bounded, and ν0(t)>0.

The communication network among the multi-robot systems is set up by onboard communication devices and sensors of each robot.To describe the communication network among theNfollower robots, a directed graph G={V,E} is adopted,where V={1,...,N} representsNfollower robots and E={(j,i):j≠i,i,j∈V} is an edge set with directed edge (j,i)representing the communication from robotjto roboti.If(j,i)∈E, then the state of robotjis available to roboti, and robotjis a neighbor of roboti; each robot has access to its own state information and its neighbors’ directly.The set of neighbors of robotiis denoted as Ni={j∈V:(j,i)∈E}.The adjacency matrix of G can be represented as A=[ai j]∈RN×N,whereaii=0, andai j=1 when (j,i)∈E, otherwiseai j=0.Let diagonal matrixbe the degree matrix of a directed graph, wheredi=j∈Ni ai j, then the Laplacian matrix of G is defined as L=D−A.In addition, to describe the communication between the leader robot and followers, diagonal matrixB= diag{b1,b2,...,bN} is defined, wherebi=1 if follower robotican get the information from the leader, andbi=0 otherwise.Also, the following assumption is made on the multi-robot systems.

Assumption 2:The directed graph among the multi-robot systems contains a directed spanning tree with the leader robotR0being the root.

Now, the destination of leader-follower formation control of multi-robot systems is to design distributed controller for each follower robotRisuch that the following objectives can be achieved.

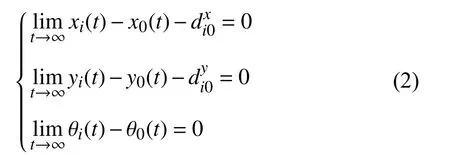
Remark 1:Equation (2) ensures that the positions of all follower robots converge to the desired geometric structure gradually.That is to say, if (2) is satisfied, the desired formation goal can be reached.

Definition 1:To facilitate the design of controller, the following formation tracking errors are defined.

Before presenting the main results, two lemmas must be introduced, which are as follows.

Lemma 1 [25]:Consider the following system:x˙=f(x),f(0)=0,x∈Rn.Suppose there exists a continuous functionV(x):U→R such that the following conditions hold:

i)V(x) is positive definite.

ii) There exist real numbersc>0 and α ∈(0,1) and an open neighborhoodU0∈Uof the origin such thatV˙(x)+cVα(x)≤0,x∈U0{0}.

Then, the origin is a finite-time stable equilibrium of the system.IfU=U0=Rn, then the origin is a globally finitetime stable equilibrium of the system.

Lemma 2 [36]:Consider a first-order system η ˙=u, where η andudenote its state and input, respectively.Take a continuous control law

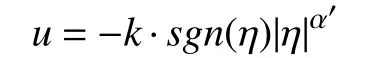
wherek>0 and α′∈(0,1),sgn(·) is the standard signum function.And the closed-loop system can be described as

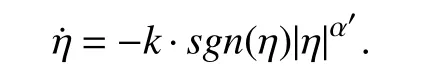
Then, there exists a finite timeTf=Vβ(0)/kβ21−β, whereV(0)=η2(0)/2, β=(1−α′)/2, such that the solution of the system converges to 0 ast→Tf, and η (t)≡0 for anyt≥Tf.

III.MAIN RESULTS

In this section, the main results will be presented in two parts.Firstly, a distributed finite time state observer for each follower robot is proposed such that the state information associated with the leader robot can be obtained in finite time.It is noted that the finite time state observer does not need the robots’ global position information.Secondly, distributed adaptive formation controllers are designed for each follower robot such that the desired leader-follower formation can be achieved and the effect of unknown slippage can be overcome.Strict stability analysis is also given.

A.Distributed Finite Time State Observer Design

Since only part of the followers can get the information associated with the leader robot, while other robots can not obtain the information from the leader directly, including the formation errorsand the velocities of the leader robot, a distributed finite time state observer was designed as follows such that each follower robot can achieved leader’s information in finite time.

Firstly, assign a virtual leader robot with statesand velocitiesfor each follower robotRi(i∈{1,2,...,N}),which can be seen as the estimations of the actual states of leader robotR0.Then, the estimated formation tracking errors of each follower robot are define d as followers:

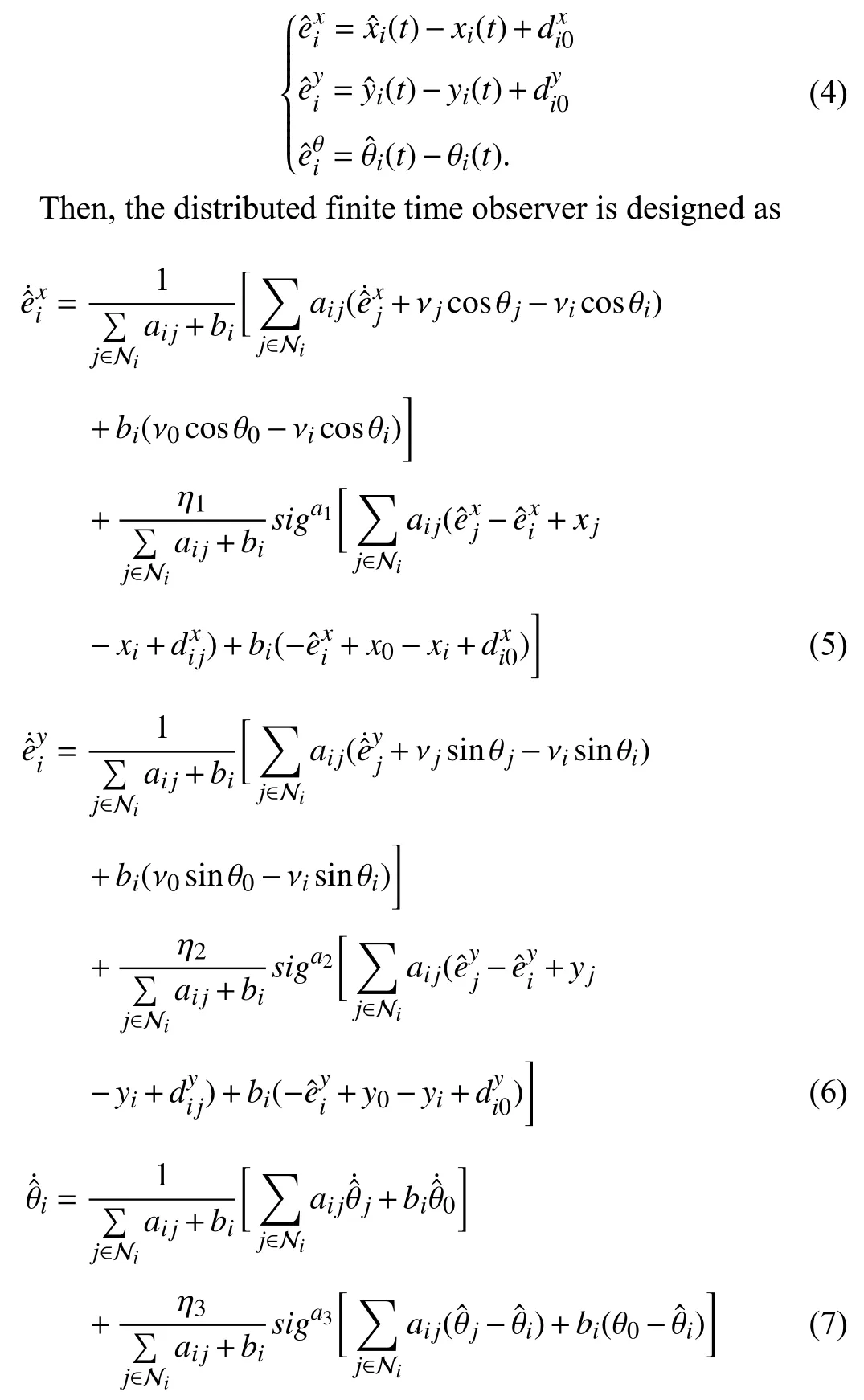
Remark 4:Compared with the distributed finite time state observer in [25], the main improvements are the proposition of (5) and (6), the state observer in [25] estimated the absolute position of leader robot directly in global coordinate system,while in this paper, no global coordinate system can be referred to, so we use (5) and (6) to estimate the relative position errors between leaderR0and followerRiinstead.

B.Distributed Adaptive Formation Controller Design

In order to solve the effect of unknown slippage on distributed formation control of multi-robot systems,distributed adaptive formation controllers [u1i,u2i]Tneed to be designed for each follower robot such that the desired formation objective can be realized.

When considering the unknown slippage, there is such a relationship between the actual control input [u1i,u2i]Tand the actual output [ νi,ωi]Tfor robotRi, which is as follows:

where [u1i,u2i]Tare the control inputs for the left and right wheels of robotRi, respectively, [η1i,η2i]Tare the actual slipping ratios corresponding to the left wheel and right wheel of wheeled robotRi, which are defined as η1i=u1i/us1i,η2i=u2i/us2i, whereus1iandus2iare actual forward velocity of left wheel and right wheel ofRidue to the existence of slippage.When η1i=1 and η2i=1, then there is no slippage.In addition,the slipping ratios should satisfy the following assumption.

Assumption 3:The slipping ratios η1iand η2iare bounded but unknown constant.

Before designing the distributed formation controllers, the following coordinate transformation (17) and (18) need to be defined first.

Remark 5:When designing the distributed adaptive formation controller, each follower robot can not use any global position information.In addition, it is necessary to ensure that the output of the designed controller is bounded.

Taking the derivative of (18), one can obtain the tracking errors space model of wheeled mobile robotRias follows:

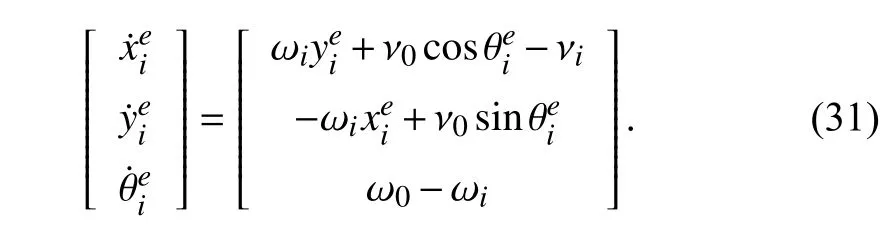
In order to prove the stability of the formation controller(26), a new state variableneeds to be defined as follow:

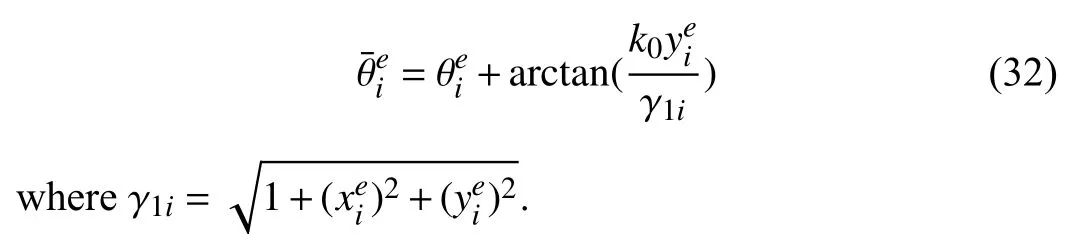
Taking the derivative of (32), one has

IV.SIMULATION RESULTS

In this section, the effectiveness of the proposed finite time state observer (5)−(8) and distributed adaptive formation controllers (20)−(25) in Section III are verified by simulation.The communication topology among the multi-robot systems adopts a directed graph satisfying Assumption 2, which is shown as Fig.2.By default, all variables are in SI units.The desired relative positions between leader and followers are selected as=[−30−30 0 30 30 −60 30 90 60]Tand=[0 −30 −30 −30 0 −60 −60 −60−90]T, as shown in Fig.3.The leader robotR0starts from[x0(0),y0(0),θ0(0)]T=[0.5(m),1(m),π/6(rad)]T, and the velocities ofR0are chosen as ν0(t)=3.25−0.25cos0.24t(m/s)and ω0(t)=0.1cos0.2t(rad/s).The actual slipping ratios are set as η1i=1.5 and η2i=1.25,i=1,2,...,N, which are unknown for each follower robot.Note that the friction coefficient of different wheels can be different.The control parameters of follower robots are chosen ask0=0.9,k1i=10,k2i=15,λ1i=12,λ2i=4,i=1,2,...,N.

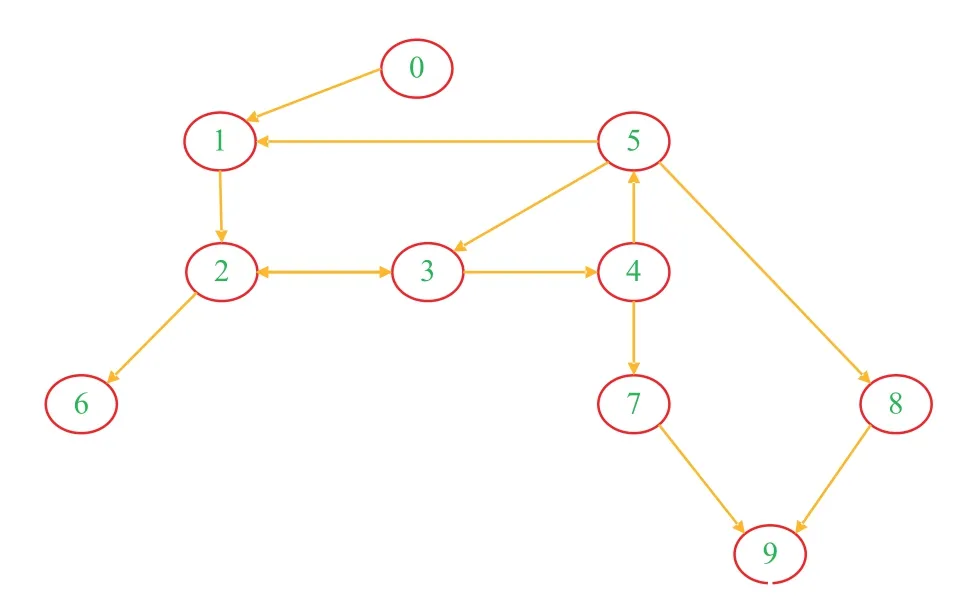
Fig.2.Communication topology among the multi-robot systems.

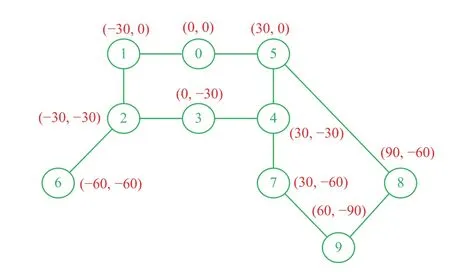
Fig.3.Desired formation of the multi-robot systems.

Fig.4 presents the trajectories of all robots during 0 −100 s.It can be seen from the figure that the multi-robot systems converges to the desired formation pattern (as shown in Fig.3)gradually from the initial pattern (represented by circles in Fig.4), which shows the proposed algorithm achieves the desired effect.

Fig.4.Trajectories of all robots.

Fig.5 shows the estimated formation tracking errorsconverge to the true values.Fig.6 shows that the observation errors between observed and true values of the leader’s velocity and angular velocity converge to zero.The two figures verify the effectiveness of the finite time state observer.

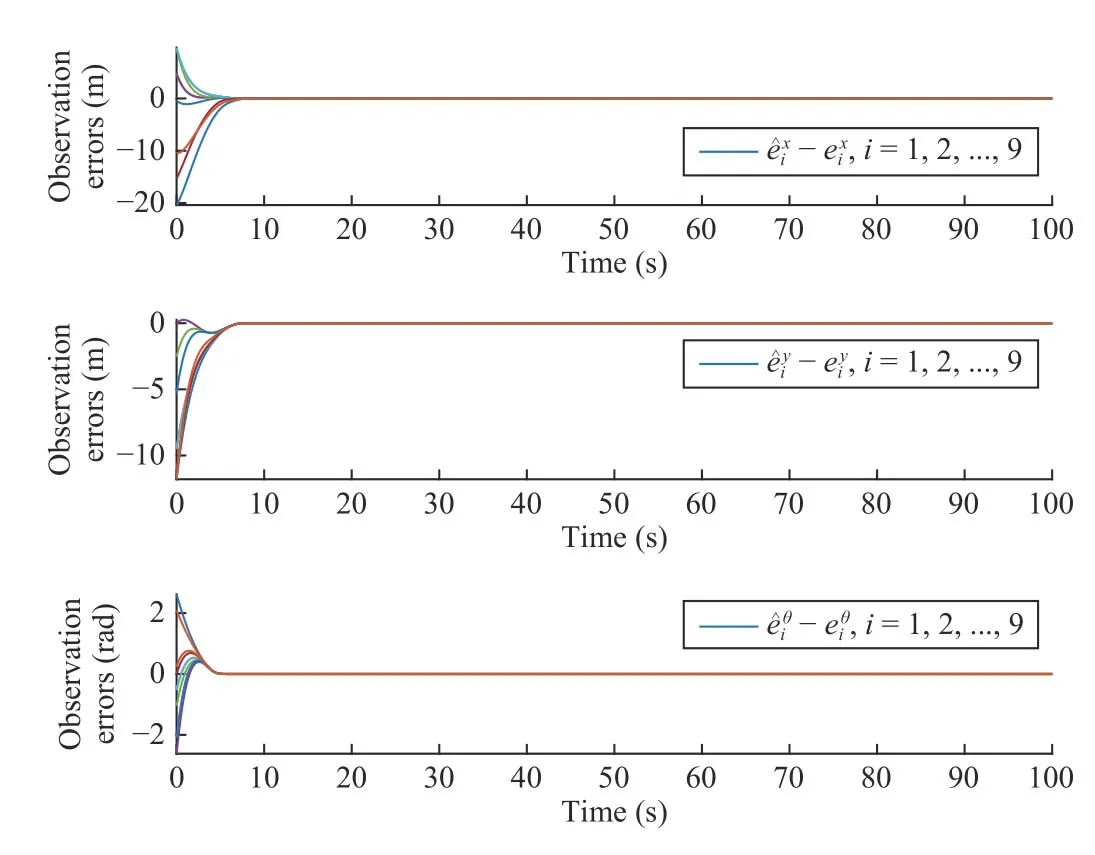
Fig.5.Formation tracking observation errors of follower robots.

Fig.6.Velocity and angular velocity observation errors of follower robots.

Figs.7 and 8 show the estimated valuesunknown slipping ratios converge to the true values [η1i,η2i]Tgradually.In addition, it can be seen from Fig.9 that all the tracking errorsof each follower robot converges to zero gradually.That is the proposed adatptive formation control algorithm can achieve the desired formation while overcoming the unknown slippage.

In order to test the robustness of the designed controllers to the change of slipping ratios, slipping ratios are chosen as η1i=1.5 and η2i=1.25 when 0 ≤t<30 s, η1i=24 and η2i=20 when 30 ≤t<60 s, η1i=3 and η2i=2.5 whent≥60 s,i=1,2,...,N.Then running the simulation again, one can get the formation tracking errors of all followers as Fig.10.It can be seen from the figure that when changing the slipping ratios a lot, it has little influence on formation errors, which means the proposed controllers have good robustness to the change of slipping ratios and are more applicable.According to the simulation results above, the effectiveness of the proposed controllers is verified.

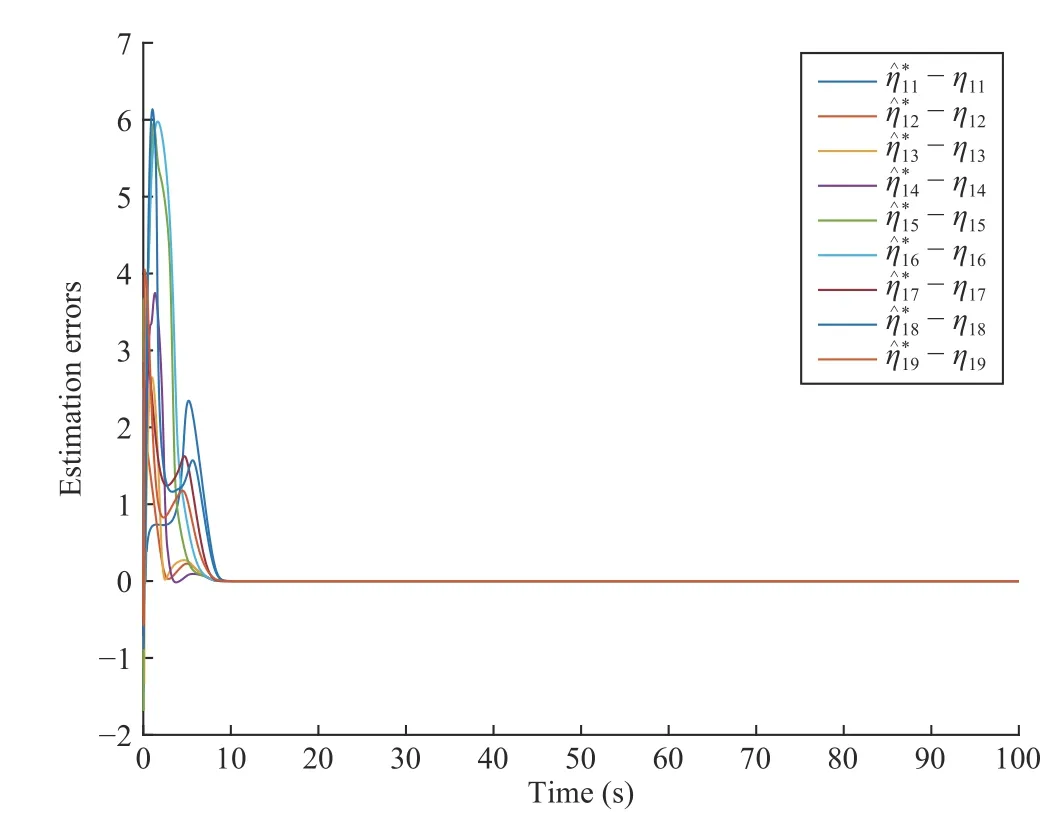
Fig.7.Estimation errors of slipping ratio (left wheel of each robot).

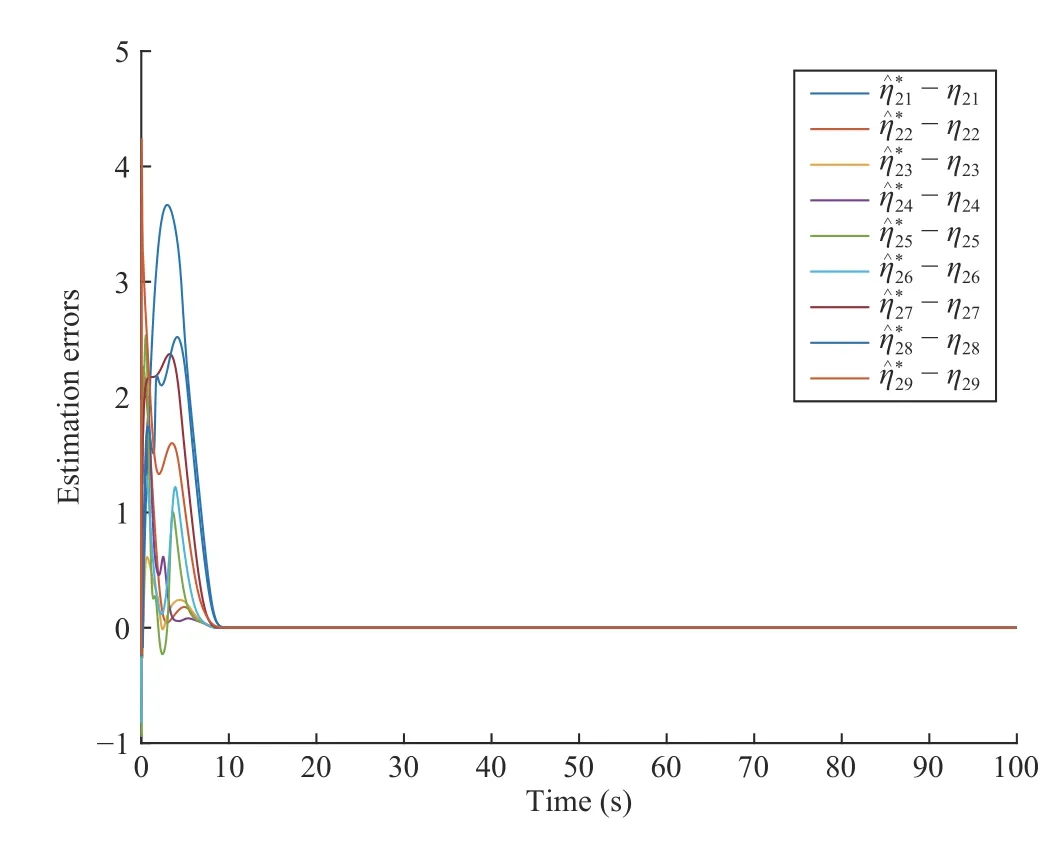
Fig.8.Estimation errors of slipping ratio (right wheel of each robot).

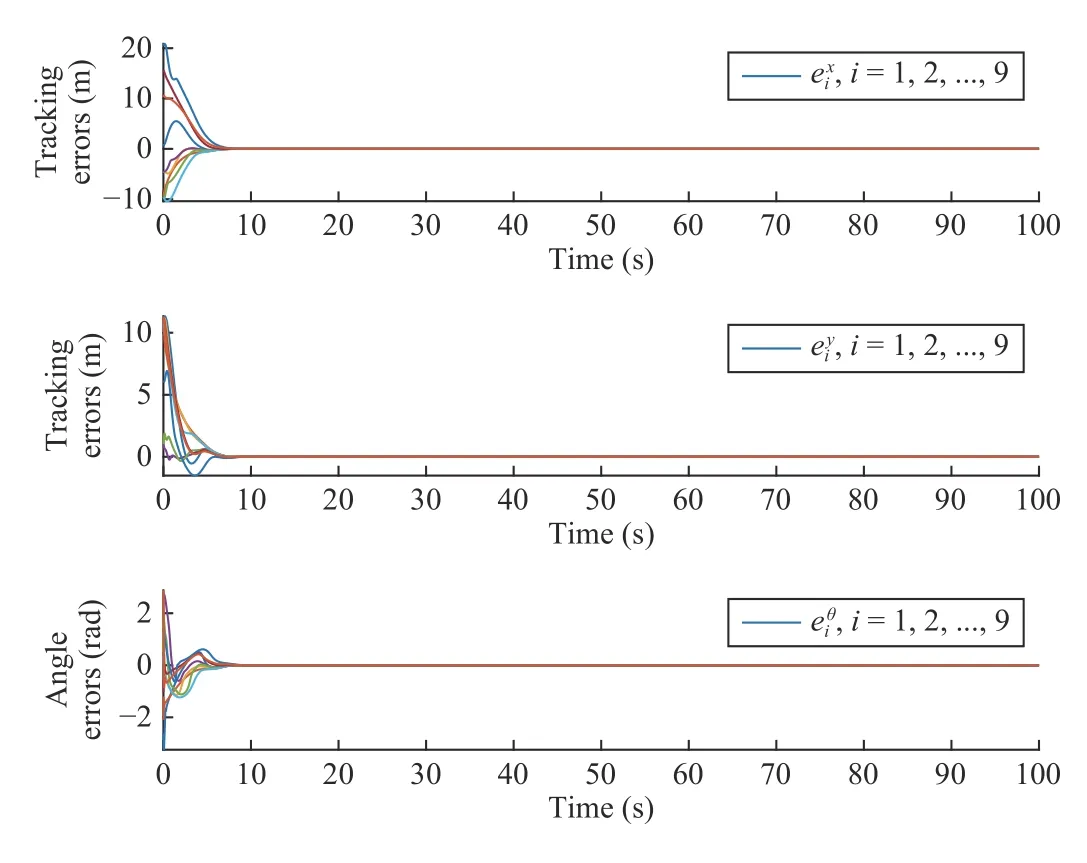
Fig.9.Formation tracking errors of all follower robots.

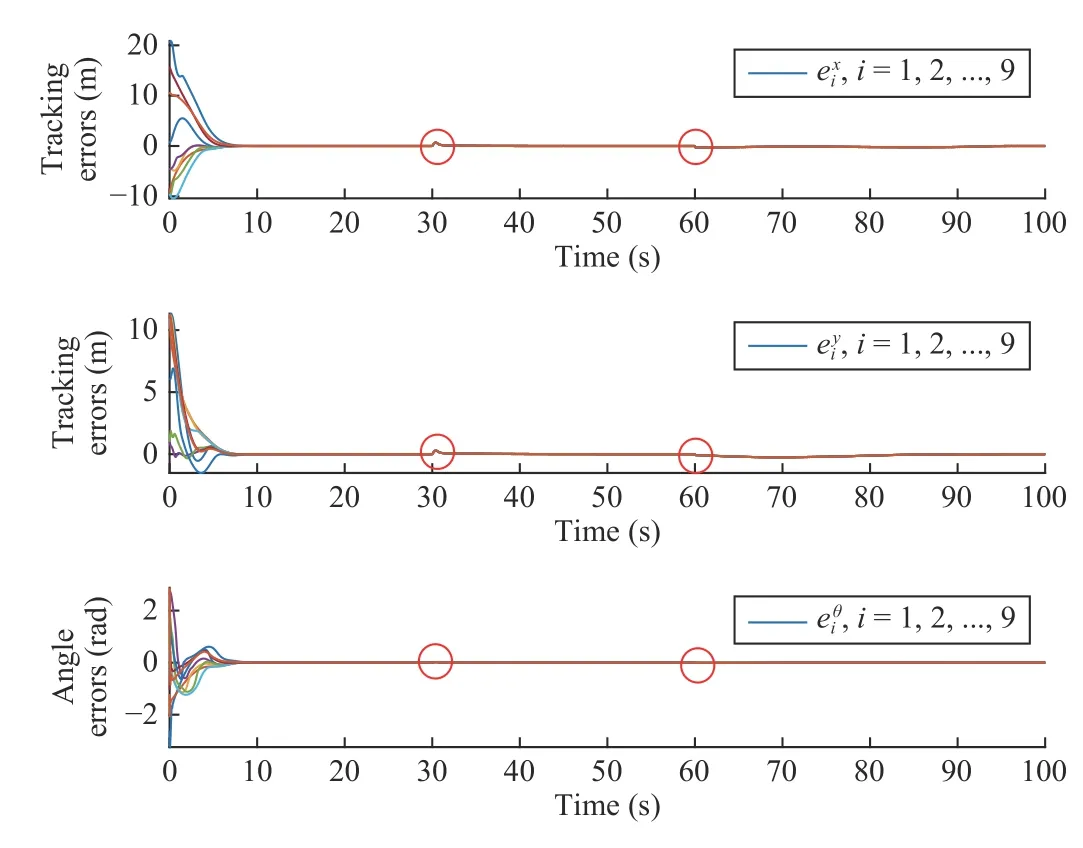
Fig.10.Formation tracking errors of all follower robots when slipping ratios change.

V.CONCLUSION

In this paper, distributed formation control problem of multi-robot systems without global position information and subject to slippage constraints is studied.The formation pattern of the system adopted is leader-follower structure and the design process can be divided into two parts.Firstly, a distributed finite time state observer without using global position information is designed such that each follower robot can estimate leader’s states in finite time.Secondly, a distributed adaptive formation controller is designed for each follower robot such that the desired formation objective can be achieved while overcoming the effect of unknown slippage.Finally, the effectiveness of the proposed observers and controllers are verified by simulation.In this paper, the communication topology among multi-robot systems is assumed to be fixed and communication delay is not considered.Hence, future works will take these factors into account.