Fault Accommodation for a Class of Nonlinear Uncertain Systems With Event-Triggered Input
2022-01-25DongZhaoandMariosPolycarpou
Dong Zhao, and Marios M.Polycarpou,
Abstract—The event-triggered fault accommodation problem for a class of nonlinear uncertain systems is considered in this paper.The control signal transmission from the controller to the system is determined by an event-triggering scheme with relative and constant triggering thresholds.Considering the event-induced control input error and system fault threat,a novel eventtriggered active fault accommodation scheme is designed,which consists of an event-triggered nominal controller for the time period before detecting the occurrence of faults and an adaptive approximation based event-triggered fault accommodation scheme for handling the unknown faults after detecting the occurrence of faults.The closed-loop stability and inter-event time of the proposed fault accommodation scheme are rigorously analyzed.Special cases for the fault accommodation design under constant triggering threshold are also derived.An example is employed to illustrate the effectiveness of the proposed fault accommodation scheme.
I.INTRODUCTION
A.Fault Accommodation
FAULT accommodation and reconfigurable control have drawn a lot of attention in recent decades due to their potential to enhance system safety and fault tolerance.Application examples of fault accommodation have been widely reported in the literature,including chemical processes,aircraft systems,unmanned aerial vehicles,and power systems [1],[2].Overall,fault accommodation is considered an important technology in modern industrial control systems.
Fault accommodation methods can be classified into active schemes and passive schemes.Active fault accommodation is used in conjunction with a fault diagnosis scheme and is initiated after a fault (or a specific event) is detected.Passive fault accommodation consists of a control scheme that is sufficiently robust to withstand a class of faults that may arise.Due to the support of fault diagnosis information,the conservativeness of active fault accommodation schemes can be reduced and its overall performance can be improved,compared to passive accommodation schemes [3]–[5].Many elegant results on active fault accommodation have been reported both for linear and nonlinear systems.A new faulttolerant control method for multiagent systems is proposed in[5],where the designed reinforcement learning algorithm can deal with the fault issue and reduce computational burden efficiently.In [6],a combined fault estimation and compensation method has been considered for linear systems with application to winding machine.Sensor fault estimation and fault accommodation have been studied in [7],where a sliding mode observer is employed to deal with the nonlinearity of the measurement process.Note that the direct fault estimation and compensation scheme requires matching conditions (or rank conditions with respect to system matrices) and is suitable for a special class of processes (in most of the cases,linear systems are considered).Optimization based fault-tolerant control has been addressed in [8],[9],where these schemes are driven by data and thus can be implemented online.An alternative fault accommodation scheme,especially for nonlinear system,is based on adaptive or (fuzzy or neural network based) adaptive approximation methods.In this case,the fault is handled in the framework of adaptive control[10]–[13].
B.Event-Triggered Control
Recently,with the development of networked systems,aperiodic signal transmission for control has been considered as a way to save communication resources,which has resulted in the use of event-based/triggered control.The basic idea of event-triggered control is to “exploit the performance potential” of control system to trade for communication/transmission cost reduction.General static and dynamic eventtriggered control solutions for linear and nonlinear systems have been proposed [14]–[20].Specifically,the eventtriggered real time control task scheduling for nonlinear system has been studied and the inter-event time was explicitly analyzed as in [21].Following the inter-event time discussion in [21],a distributed event-triggered control solution for linear multi-agent system was reported in [22].Also,dynamic event-triggered control based on a filtered triggering signal has been developed and analyzed [23].Regarding the control schemes for event-triggered nonlinear continuous-time systems,mostly,such control schemes are implicit asK(x),and they are determined by using the input to state stability theory with event-triggered sensor to controller communication [14],[21]–[24].Moreover,an event-triggered controller was proposed to deal with process disturbance in[15],while robust controllers that consider modeling uncertainties were presented in [25]–[28].
Summarizing these results on nonlinear system eventtriggered control,research efforts are mainly made on input to state stability analysis,inter-event time discussion,and new triggering scheme design.
C.Event Triggered Fault Accommodation
In the case of nonlinear event-triggered control in the presence of faults,some results have been reported,where the event-triggered control with actuator parameter/gain fault was addressed in [26],[27],[29] and fuzzy fault-tolerant control in the framework of impulse controller and system modeling for nonlinear system with event-triggered measurement was considered in [30].Finite time control with fuzzy nonlinear process dynamics and fault approximation was examined in[31].It is noted that in [26],[27],[29]–[31] the proposed methodologies were based on passive accommodation schemes,with the considered actuator faults modeled by bounding parameters.The event-triggered active fault accommodation design problem,where the fault is state dependent,has not yet been addressed in the literature.Besides,for a more in-depth study,the influence of relative and constant event-triggering threshold on fault accommodation design and implementation has not been carefully investigated.
In this study,we focus on the design and analysis of a fault accommodation scheme for a class of nonlinear systems subject to modeling uncertainties and event-triggered control input.Different from [26],[27],[29],[30],we do not assume global (known) bounds or specific dynamics for the fault model.Anactive fault accommodation schemeis proposed,where targeted controllers are designed for different fault and detection situations.In this framework,no input to state stability assumption with respect to sampling error is needed[14].To reduce the communication burden and protect the actuator,the control signal transmission from the controller to the system is determined by an event-triggering scheme.Based on this event-triggered signal transmission scheme,a novel fault accommodation scheme is proposed to deal with the potential system fault and event-induced error.The fault accommodation scheme consists of a nominal controller for the period before a fault is detected and an adaptive approximation-based event-triggered fault accommodation law for the period after a fault is detected,where a neural network model is used to approximate the unknown process fault effect.The stability of the event-triggered control system is rigorously analyzed.A bounded control performance can be guaranteed with a non-zero lower bounded inter-event time.Regarding the obtained fault accommodation controllers corresponding to both relative and constant triggering thresholds,we provide the effect analysis of event-triggering scheme on the adaptive approximation based fault accommodation design and implementation.
The main theoretical challenges in this study are i)quantifying the event-induced discrepancy for control design,ii) Zeno-behavior free fault accommodation scheme design,and iii) the explicit upper bounds of the tracking error with the event-triggered controllers.The main contributions of this work are summarized as follows:
1) event-induced signal discrepancy for fault accommodation design is explicitly quantified;
2) adaptive approximation based fault accommodation design under event-triggered control effort implementation is proposed,where thetime periods before fault occurrence,after fault detection,and within the fault occurrence and detection are all considered;
3) explicit upper bounds on the tracking error are derived for the event-triggered fault accommodation system before and after the detection of system fault;
4) relative and constant event-triggering threshold influence on fault accommodation controller structure design and implementation are investigated.
The rest of the paper is organized as follows.Detailed problem formulation is presented in Section II.The eventtriggered nominal controller design and performance analysis are provided in Section III.The fault accommodation controller design and analysis are given in Section IV.In Section V,constant triggering threshold case is discussed followed by controller solutions.A single-link robot example is included in Section VI to illustrate the effectiveness of the proposed controllers.Concluding remarks are provided in Section VII.
Notations:A positive (negative) definite matrixPis denoted asP>0 (P<0).Inis andimensional unity matrix.For vectorsaandb,col{a,b}=[aT bT]T.For any real scalarαand vectorβ,|α| a nd ‖β‖pare respectively the absolute value ofαandpnorm ofβ(p=1,2,∞).For the time functions in this study,we omit the time variabletfor simplicity if it is clear from the context.
II.PROBLEM FORMULATION
Consider the following class of nonlinear uncertain systems[32]:
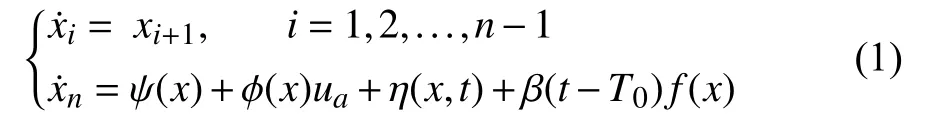
wherex=col{x1,...,xn} is the system state andua:R+→R is the control input.The initial value of (1) is denoted asx0,while ψ(x):Rn→R and φ(x):Rn→R are continuously differentiable functions characterizing the known nominal system dynamics (φ (x)≠0 for allx),and η (x,t):Rn×R+→R is a continuous function denoting the unknown and unstructured modeling uncertainty.The functionf(x):Rn→R characterizes the unknown change in the system dynamics resulting from a fault,which is referred to as fault function in the following and assumed to be continuous.The function β(t−T0)is the fault time profile function [10],given by
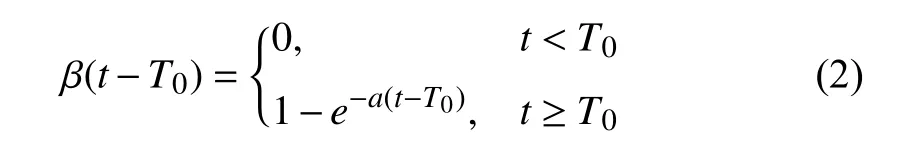
wherea>0 is an unknown constant representing the fault evolution rate andT0>0 is the unknown occurrence time of the fault.In the case thatais relatively large,β(t−T0)approaches a step function,which denotes an abrupt fault;in the case thatais relatively small,incipient (slowly developing) faults can be modeled.
To reduce the communication burden and to extend the lifetime of the actuator,an event-triggering scheme is considered for the transmission of the control effort signal from the controller to the actuator.Specifically,a monotonically increasing sequence τkis defined to denote the corresponding transmission/triggering times:
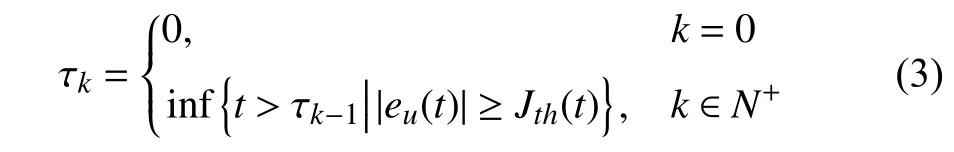
whereeu(t)=u(t)−ua(t) andJth(t)=γ|ua(t)|+ω.The design parameters γ ∈[0,1) and ω ∈R+are used to balance the relative change and absolute change,respectively,in the triggering thresholdJth[14].Note thatu(t) is the controller output andua(t),as introduced in (1),is the implemented control effort by the actuator due to the event-triggering scheme.Following the determined triggering time in (3),we have:
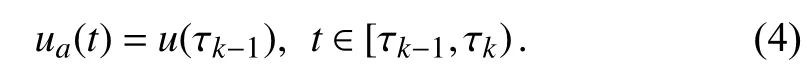
Based on (3) and (4),it can be seen thatωdominates the triggering threshold when γ →0 .On the other hand,as γ →1,the magnitude ofu(t) affects the triggering threshold.Specifically,a large (small) magnitude ofu(t) is accompanied with a large (small) triggering threshold.Hence,γserves to adjust the control effort effect on the triggering frequency[15],[26],andωcan keep a non-zero triggering threshold for the case thatu(t) approaches zero.Sinceua(t) is a function with respect to time,the adopted event-triggering thresholdJth(t)is not static but adaptive.
An active fault accommodation scheme is initiated after a fault is detected at timeTd.In this study,we consider the design of event-triggered fault accommodation strategies before and after the detection of the occurred fault.Since only the fault detection informationTdis needed andTdis the basic output of any fault detection scheme,the event-triggered fault accommodation strategy is independent of the structure of the fault detection scheme,and the reconfiguration of the fault accommodation scheme is feasible.Thus,any of the existing fault detection methods can be combined with the fault accommodation scheme developed in this work (please see[33],[34] and references therein for various fault detection methods).
Due to an essential response time for the fault detection scheme,a non-zero fault detection delay between the occurrence and the detection of a fault is inevitable;i.e.,Td>T0.The magnitude of the fault function during the fault detection delay time periodt∈[T0,Td] is required to satisfy the following assumption.
Assumption 1:ForT0≤t≤Td,the fault function satisfies|f(x(t))|≤εf,where εfis an unknown positive scalar.
Assumption 1 implies that the magnitude of the fault function remains bounded before the fault is detected.It is a reasonable assumption for control systems [10],since it becomes easier for the fault detection scheme to detect the fault as the magnitude of the fault function increases.
The following assumption will be used for the controller design.
Assumption 2:For allx∈Rnandt∈R+,the modeling uncertainty η (x,t) satisfies

In this study,to keep the generality of the control formulation,the tracking problem is considered.The desired tracking signalxd(t)=[r(t) ···r(n−1)(t)]Tandr(n)(t) are bounded and continuously differentiable references,wherer(t)is an external reference signal.The objective of this paper is to develop a rigorous fault accommodation strategy forx(t)in (1) to trackxd(t),taking into consideration the eventtriggering scheme defined in (3) and (4),and the presence of an unknown fault.Specifically,an event-triggered nominal controller is proposed fort≤Td,which covers the fault-free case (t
Remark 1:From the aspect of control,system control performance may be seriously affected by inaccurate feedback,especially when facing a critical threat of fault.Thus,we address the event-triggered control signal transmission and actuator updating problem,and keep the essential measurement for ensuring fault accommodation performance.
Remark 2:As discussed in Section I,there are various event-triggering schemes reported in the literature.To address the fault accommodation problem,we adopted a general static triggering scheme,given by (3) and (4),where the triggering threshold consists of both relative and constant parts.Since the main objective of this work is the design of a fault accommodation scheme while taking into consideration the event-triggering effect,the investigation of more advanced triggering schemes (e.g.,dynamic triggering scheme or periodically triggering scheme) can be integrated into the fault accommodation design,which can be studied in the future.
III.EVENT-TRIGGERED NOMINAL CONTROLLER DESIGN AND ANALYSIS
In this section,we present the nominal controller design,stability analysis,and inter-event time analysis for the eventtriggered control system of (1) whent≤Td.
A.Event-Triggered Nominal Controller Design
Define the tracking error as=x−xd.Considering the event-triggered control effect implementation,the original system (1) is rewritten with respect toanduaas
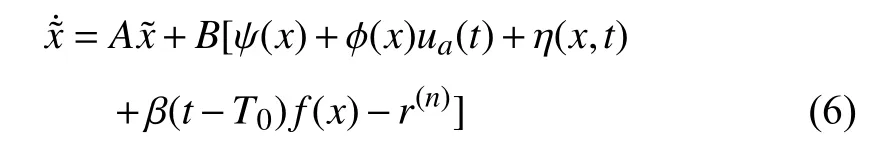
where
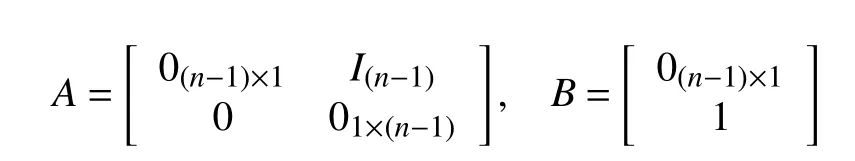
Note thatua(t) is determined by (4).
Prior to the detection of a system fault,the nominal eventtriggered control is designed as follows:
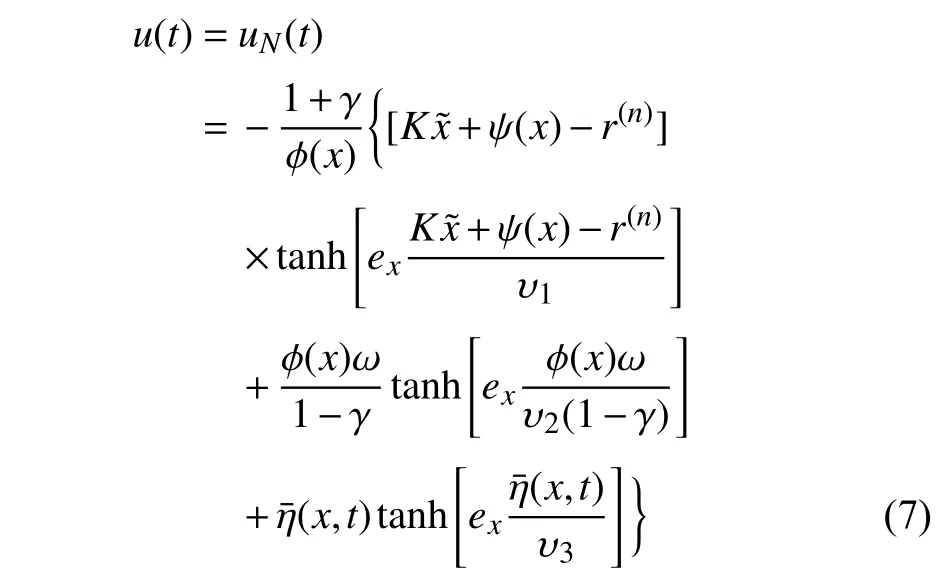
In the following,we provide some intuition regarding the event-triggered nominal controller in (7).
1) The nominal controller structure in (7) consists of three terms which are respectively multiplied bytanhfunctions,where the first term corresponds to the nominal system dynamics,the second term results from the event-triggered control effort implementation scheme,and the third term is used to bound the modeling uncertainty.The need of the three terms and the role of thetanhfunction will become apparent from the stability and the inter-event time analyses.
2) The event-triggering parametersγandωare integrated in the nominal controller.The larger the event-triggering parametersγandωare,the larger the magnitude of the control effort could be.This design is inspired by the fact that larger event-triggering parameters lead to larger event-induced discrepancy.If |ex| is relatively large,|tanh(ex)|→1;on the other hand,|tanh(ex)|→0 when |ex|→0.Thus,the controller in (7) has an “adaptive gain” regarding the magnitude of tracking error.
B.Stability Analysis of the Event-Triggered Nominal Control Systems
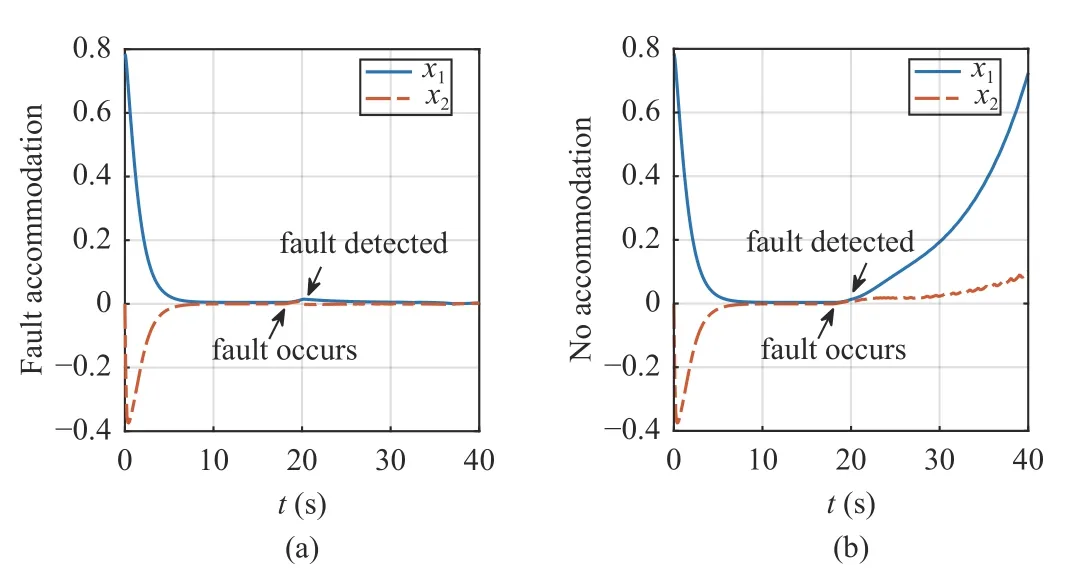
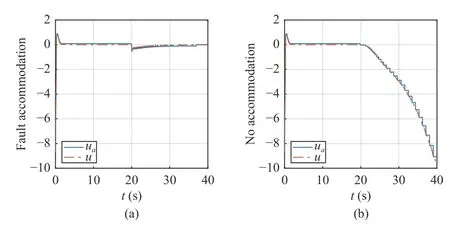
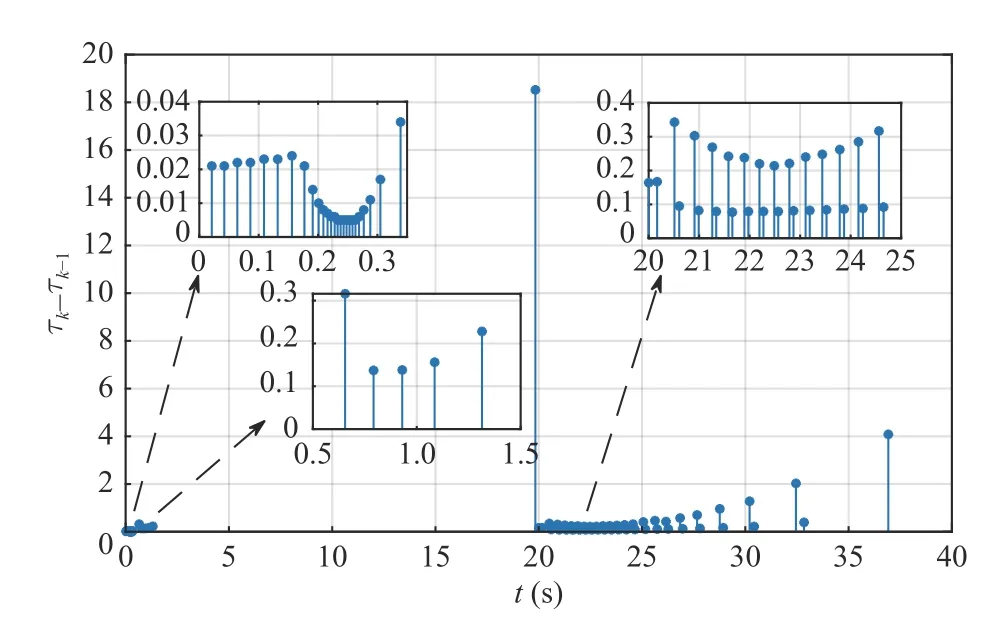
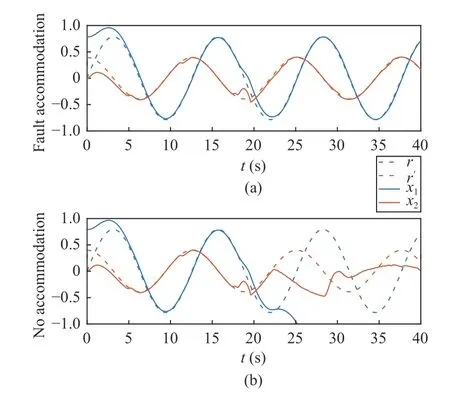
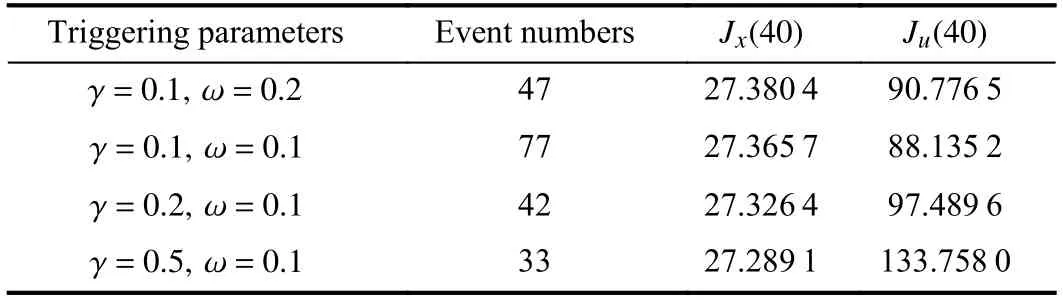
The nominal controller is used before a fault is detected,which corresponds to both the fault-free time period(0 ≤t First,let us consider the fault-free time period (t According to (6),the time derivative ofVis given by Recalling the event-triggering scheme defined in (3) and(4),fort∈[τk−1,τk),we rewrite the inequality in (3) as an equation to characterize the difference between the controller outputuand the actuator outputua whereuNis given in (7).Thus,referring to the definitions ofKandP,the following inequality holds: Next,we utilize the following lemma. Lemma 1 [35]:For alla∈R+andb∈R,it holds that Substitutingufrom (7) into (16) and using Lemma 1 and inequalities in (19) and (18),we obtain whent>T.Hence,the event-triggered nominal controller in(7) can ensure that the tracking error of system (1) is uniformly ultimately bounded in the absence of system faults.In addition,by tuningcυandδ,we can get an arbitrary small asymptotic bound for(t). Next,we consider the time period of fault detection delay(T0≤t≤Td),where the nominal controller (7) is used,but β(t−T0)f(x)≠0.In this case,the time derivative ofVsatisfies SinceQ>0,there exists a positive scalarχsuch thatQχ=Q−χI>0 (e.g.,χ <σmin(Q)).Note that Referring to Assumption 1,we obtain Similar to the derivation for (21),we can conclude from(24) that there existsTF>T0such that The following Theorem summarizes the closed-loop stability results with the nominal event-triggered controller. Theorem 1:Consider the nonlinear uncertain system (1)subject to Assumptions 1 and 2.The event-triggered controller(7) with the triggering implementation scheme (4) and (5)guarantees that the tracking error(t) satisfies the following properties: i) in the absence of a fault,∃T>0 such that (21) holds for allt>T; ii) in the presence of a fault,∃TF>T0such that (25) holds for allt>TF. Theorem 1 presents the stability properties of the nominal controller under event-triggered actuation.The explicit final tracking error bounds are investigated.Uniformly ultimately bounded control performance can be guaranteed based on the nominal controller before and after the fault occurrence.In the following,the analysis of inter-event time for the eventtriggered nominal controller is given. Since the system described by (1) evolves in a continuoustime manner,it is important to check the evolution of the inter-event time τk+1−τk.We expect that a non-zero lower bound exists for the inter-event time such that the communication load is low (i.e.,Zeno behavior can be excluded [15]). For the event-triggering scheme,a key idea is to check the varying rate (time derivative) of the controller output.According to (3) and (4),fort∈[τk,τk+1),one has Next,we investigate the triggering threshold.Withγ ∈[0,1)and ω>0,the pre-determined thresholdJthis non-zero.We have τk+1−τk≥τmin=,wherek∈Nandt≤Td.Sinceuais not zero for most of the time andθis an upper bound,the real inter-event time will be larger than τmin,and the Zeno behavior of the proposed event-triggered nominal controller is excluded. In practice,the controller parameters υi(i=1,2,3) will also affect the inter-event time.As υibecome smaller,although the tracking performance improves according to (20),the varying speed of the controller output may increase at some intervals since tanh(x/υi) approaches a step function as υi→0.Hence,there exists an inherent trade-off between the tracking performance and the inter-event time. After the occurred system fault is detected,the eventtriggered nominal controlleruN(t) is reconfigured by a fault accommodation controlleruD(t) to compensate the fault effect. For the convenience of implementation,the following modular fault accommodation controller is presented: whereuN(t) is the nominal control effort presented in (7) anduF(t)is the control effort to be designed for compensating the fault effect in the control system. The occurred process fault functionf(x) is approximated by the following linearly parameterized neural network approximation model: where ϑ ∈Rnϑis the adjustable neural network weight vector andg(x) is a vector of preselected smooth basis functions. The network model (28) offers an on-line approximation for the unknown system faultf(x).However,in practice there will be an approximation error betweenf(x) andfˆ(x,ϑ) even if an optimal ϑ=ϑ∗is selected.To characterize the approximation error,ϑ∗is defined as follows: where ϑ∗is the unknown optimal neural network weight vector andX⊂Rnis a compact set that includes the region of interest. Based on ϑ∗,the following assumption is made. Assumption 3 characterizes the upper bound of the approximation error for the unknown system fault,and it follows from the general approximation-based control [10].Based on Assumption 3 and the approximator of (28),the tracking error dynamics of (6) can be rewritten as Since the fault evaluation rateain (2) and the upper bound of fault approximation error (λ) are both unknown,to address the parameter uncertainty in (22),the following parameter is introduced: 2) the event-triggering parameterγis integrated into the fault accommodation effort,where the magnitude of the compensation effort is proportional toγ. Finally,the adaptive bounding technique is used for synthesizinguF(t),combining the estimations with the known information of the lumped variables.Due to the event-induced parameter uncertainty,when γ ≠0,a large fault accommodation effort is designed to ensure the fault tolerance.This is the cost for the control signal transmission/updating reduction. Remark 3:The use of neural networks and adaptive approximation methods to estimate a fault function has previously been used in the literature,e.g.,[10],[11],[13].In this study,the key contribution is to integrate adaptive approximation with an appropriate event-triggered control design such that fault accommodation can be achieved. Remark 4:The event-triggered fault accommodation scheme in (27) is based on the nominal controller with the accommodation effort described as an auxiliary signal to the nominal effort.Nevertheless,it should be noted that the design of the nominal controller and the fault accommodation controller can be decoupled;therefore other existing eventtriggered control schemes can be combined with the proposed event-triggered fault accommodation scheme,if the control performance within the fault detection delay time period can be ensured as in this study.Benefiting from the modularized structure of (27),a target fault accommodation effort is designed (different from the passive scheme,e.g.,[30],[31]);thus the conservativeness is reduced and the portability of the proposed fault accommodation scheme is ensured. To examine the closed-loop stability of the overall control system after the fault accommodation scheme is initiate,we use a Lyapunov function Generally,event-triggered control involves a trade-off between communication burden and control performance.The general control performance sacrifice comes from two parts.First,the design freedom of the controller is limited.The basis functions for the neural network-based approximation are smooth.In this study,the “sgn” function,which is usually used in adaptive bounding design,is avoided in order to exclude the potential Zeno behavior.In general,the “sgn”function leads to enhanced performance in the absence of measurement noise.It is noted that if we replace the “tanh”function by the “sgn” function,we can obtain asymptotic tracking performance.Despite this tradeoff,the controller parameters can be tuned to reduce the upper bound of the tracking error to a reasonable level.Second,extra requirements on system dynamics and fault are needed such that the varying speed of the controller output is upper bounded [15].In this study,it is known from (20) and (35)that the tracking error cannot be made arbitrary small by just adjusting the controller parameters due to the requirement for keeping the appropriate inter-event time. Remark 5:For the event-triggered fault accommodation strategy proposed in this study,the controller reconfiguration is essential.However,this one-time controller reconfiguration makes the controller output discontinuous att=Td,and one event may be triggered.Since the varying speeds ofuN(t) anduD(t) are all bounded,the one discontinuous point att=Tdfor controller output will not change the Zeno behavior exclusion property of the proposed event-triggered controllers,but only one compulsive event may be added.Besides,one may view the considered fault accommodation system as a very special case of a switched system,where only one time of switching for system dynamics and controllers is triggered,and the switching order is fixed. Regarding the event-triggering scheme described in (4) and(5),it is of interest to discuss some special cases,based on the obtained fault accommodation controller. If we let γ=0 in (3),the triggering threshold becomesua(t)=u(t)+µ2ω.Since the multiplicative effect resulting from the event-triggered implementation on the control effort is removed,bothuN(t) anduF(t) can be simplified.Though one can set γ=0 for the obtained controllers to get the simplified controllers,we can further simplify the unessential part in the obtained controllers in Sections III and IV by removing all the multiplicative uncertainties. Usingua(t)=u(t)+µ2ω,the derivation process to remove the unknown parameter µ1can be eliminated.Thus,following(16),now we have: Following the idea foruN(t) design,the event-triggered nominal controller with constant triggering threshold,denoted asuωN(t),can be obtained: Without proof,the following corollary holds based on Theorem 1. Corollary 1:Consider the nonlinear system (1) subject to Assumptions 1 and 2.The event-triggered controller (38),with the triggering implementation scheme (3),(4),and γ=0,guarantees that the tracking error(t) satisfies the following properties: i) in the absence of a fault,∃Tω>0 such that whereuωFis the fault accommodation effort corresponding to the case γ=0 in (3).Based on (32),we have The following corollary can be obtained based on Theorem 2 and Corollary 1. From (38) and (40),it can be seen that a more targeted control effort can be designed when there is no relative uncertainty resulting for the relative change portion of the triggering threshold.Thus,the controllers in (38) and (40) are much simpler than those in (7) and (32) with γ=0.Since Lemma 1 will be used less for the upper bound analysis when(38) and (40) are used,the corresponding theoretical upper bound of tracking will be smaller,compared to the case with(7) and (32). From (38) and (40),it can be seen that the fault accommodation scheme ismathematically decoupledfrom the event-triggered scheme when a constant triggering threshold is adopted.The only requirement is to ensure a “smooth” fault accommodation effort such that the Zeno behavior can be excluded (e.g.,choosing smooth basis functions for adaptive approximation).Thus,Corollaries 1 and 2 together provide a simple fault accommodation implementation framework when constant triggering threshold is used for input signal transmission:add −ωtanhto the standard nominal control signal.The modularization of the compensation control effort makes this simple implementation feasible. Remark 6:Regarding the threshold design for eventtriggering scheme,two more cases can be discussed,based on the results of this study. 1) Relative threshold of the controller output.In (3),the triggering threshold is based on the actuator output.Alternatively,we can replace the actuator output in the threshold by the controller output;in this case,ua=(1+µ1γ)u+µ2ω whent∈[τk−1,τk).Following the same procedure for dealing with the unknown parameters µ1and µ2for (7),the corresponding controller can be readily obtained as: 2) Tracking error based event-triggering scheme.Since a tracking problem is considered in this study,the tracking error could be integrated in the event-triggering scheme as in [27].Since the tracking error vector is known,it could be covered by the triggering threshold in (3),where the threshold comes to be γ|ua(t)|+ω+‖‖.Hence,there is no technical difference due to the composition change in constant part of triggering threshold here,compared to the scheme in (3). In this section,a single-link robot manipulator system is employed as an example for simulation study.Following [36],the model is described by: wherex1is the angular position of the link,x2is the angular velocity of the link,Jis the total rotational inertia,Bis the overall damping coefficient,mis the total mass,gis the gravitational acceleration,lis the length from the joint axis to the link center of mass,anduis the torque input. For simulation purposes,we setJ=7.7 kg,B=30.5 N.s/m,l=1 m,M=1 kg,andg=9.8 m/s2.The tracking reference vector isxd=[0 0]T.LetT0=18 s,Td=20 s,r=0.1,a=2,andf(x)=5sin(x1).The initial value of the single-link robot system isx1(0)=π/4 andx2(0)=0.The parameters for eventtriggering scheme are γ=0.1 and ω=0.1. The state profiles with the proposed event-triggered control scheme are shown in Fig.1,including the scenarios with and without fault accommodation.As seen from Fig.1,the fault accommodation controller can retain a satisfactory tracking performance even in the presence of an unknown system fault.The controller output and the implemented control effort profiles are shown in Fig.2.The inter-event times and event triggering times are shown in Fig.3.Based on Figs.2 and 3,it can be seen that many events are triggered in the time interval[0,1],where this is due to the fast state convergence with the nominal controller for this example.One can reduce the convergence speed (e.g.,smaller magnitude for the real part of the eigenvalues ofA–BK) to get fewer events. Fig.1.State trajectories of the event-triggered control system with constant reference.(a) with fault accommodation controller;(b) without fault accommodation controller. Fig.2.Controller output and the implemented control effort.(a) with fault accommodation controller;(b) without fault accommodation controller. Fig.3.The inter-event times and event triggering times. To show the tracking performance further,consider a timevarying reference case withThe simulation settings for the rest parameters are the same as introduced above.As illustrated in Fig.4,a satisfactory tracking performance can be achieved based on the proposed fault accommodation scheme. Fig.4.State trajectories of the event-triggered control system with timevarying reference.(a) with fault accommodation controller;(b) without fault accommodation controller. Based on the event-triggering scheme design,we can increaseγto reduce the event numbers in transition time period.For a more in-depth study,we adopt the indicesJx(t)=to measure the accumulated tracking error and control effort,respectively.The results of event numbers,Jx(40) andJu(40),with different event-triggering parameters,are given in Table I(constant reference).From this study we see that increasing the event-triggering parameters can lead to fewer events but larger control effort.As the event-triggering parameters affect the dynamics of the proposed fault accommodation controller,fewer events may not imply a worse tracking performance.Recalling the structure of the proposed adaptive controller,increasingγcan cause a sharp increase of control effort (see Table I),which in turn helps to bound the system fault effect.This trade-off also calls for an optimization between communication and control effort,which can be studied further.All in all,this simple simulation example illustrates the trade-off between fault tolerance and communication burden.It also illustrates the effectiveness of the proposed event-triggered fault accommodation scheme and provides some intuition on the operation of the proposed scheme. TABLE IINDICES WITH DIFFERENT EVENT-TRIGGERING PARAMETERS An event-triggered fault accommodation scheme for a class of nonlinear uncertain system has been designed and analyzed in this work.The system control input is updated when the controller output change with respect to the current system input is larger than a predefined threshold.The stability properties of the proposed event-triggered fault accommodation scheme are rigorously examined,both before and after the detection of the fault.The potential of Zeno behavior is shown to be excluded.Also,a special triggering threshold case is further discussed with explicit controller solutions.The performance of the proposed fault accommodation scheme is illustrated by an example. Due to the performance requirement of the event-triggering scheme (Zeno behavior free),the design freedom of the proposed fault accommodation scheme is limited to ensure a“smooth” control signal.Also,to compensate the eventinduced error,a relative large control force is designed,especially after a fault is detected.In the future,an eventtriggered fault accommodation scheme,which is more general in structure and economic in control effort,is worth studying to improve the overall control system performance and reduce conservativeness at the same time.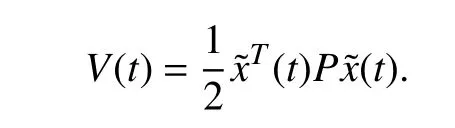
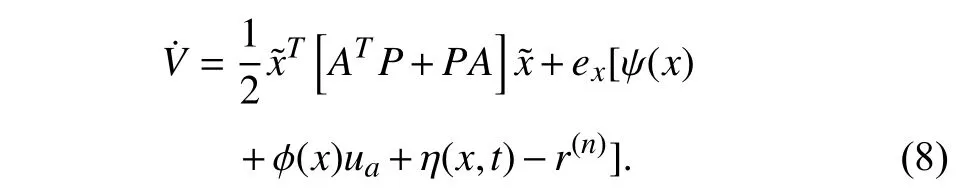

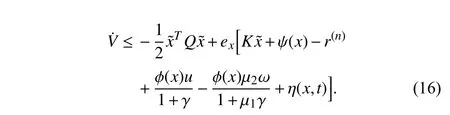


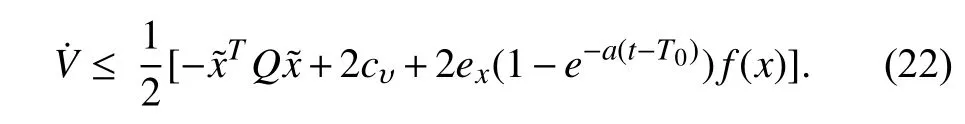
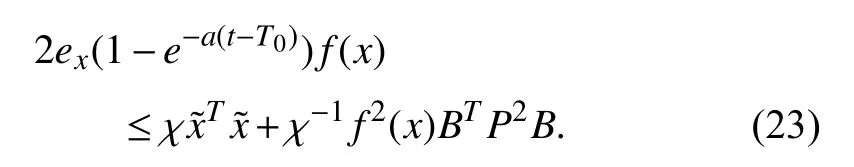
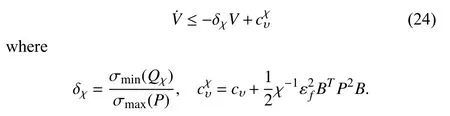

C.Inter-Event Time


IV.EVENT-TRIGGERED FAULT ACCOMMODATION SCHEME
A.Event-Triggered Fault Accommodation Controller Design
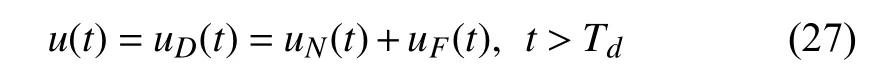

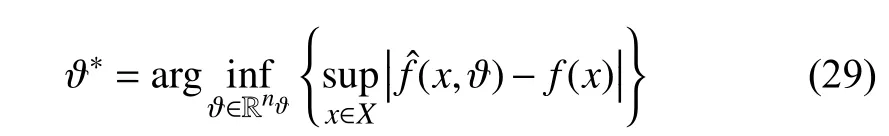
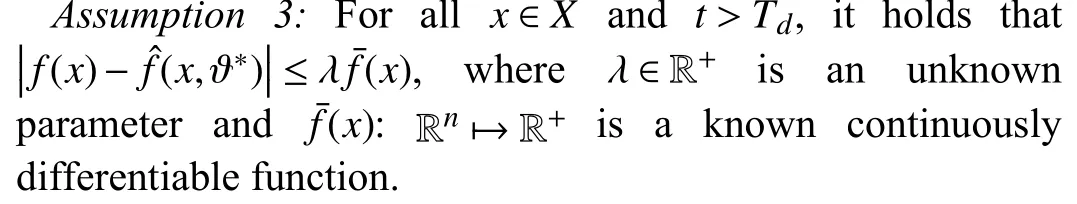
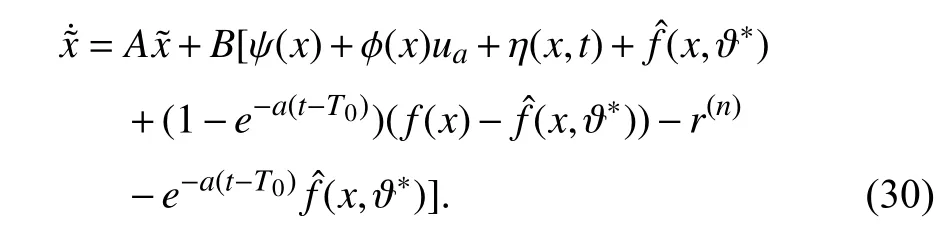

B.Event-Triggered Fault Accommodation Controller Analysis


V.CONSTANT TRIGGERING THRESHOLD
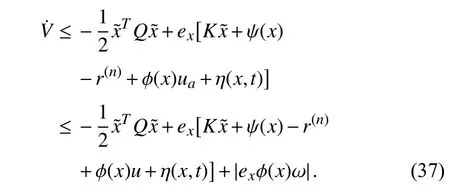
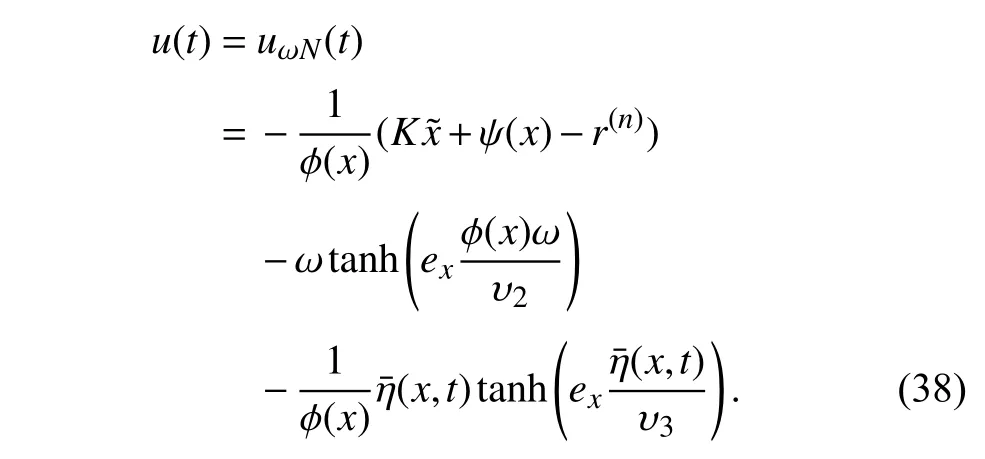

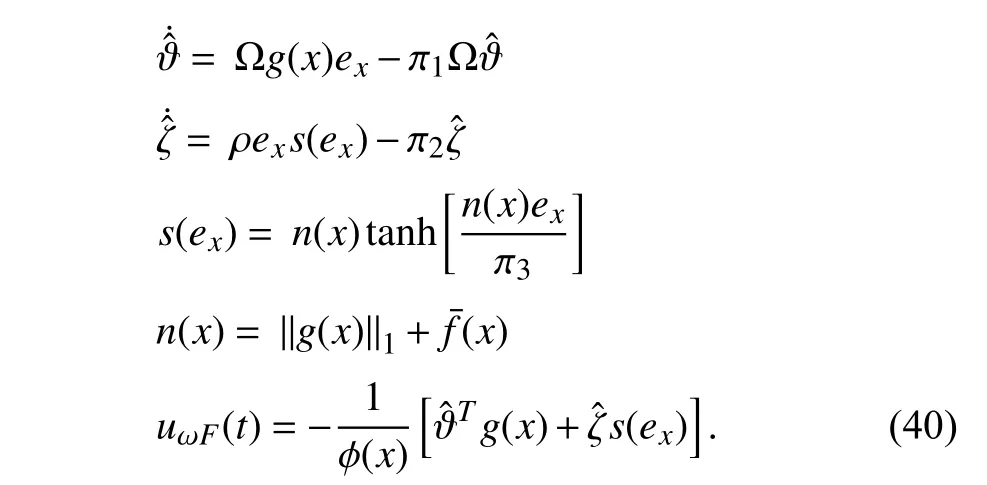


VI.SIMULATION STUDY
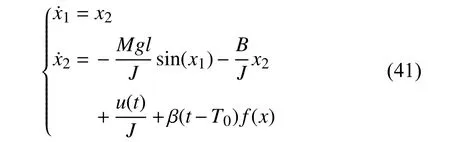

VII.CONCLUSIONS
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Sampling Methods for Efficient Training of Graph Convolutional Networks:A Survey
- Precise Agriculture:Effective Deep Learning Strategies to Detect Pest Insects
- Maximizing Convergence Speed for Second Order Consensus in Leaderless Multi-Agent Systems
- Exponential Set-Point Stabilization of Underactuated Vehicles Moving in Three-Dimensional Space
- An Adaptive Rapidly-Exploring Random Tree
- Aerodynamic Effects Compensation on Multi-Rotor UAVs Based on a Neural Network Control Allocation Approach
