Maximizing Convergence Speed for Second Order Consensus in Leaderless Multi-Agent Systems
2022-01-25GianvitoDifilippoMariaPiaFantiandAgostinoMarcelloMangini
Gianvito Difilippo,Maria Pia Fanti,,and Agostino Marcello Mangini,
Abstract—The paper deals with the consensus problem in a leaderless network of agents that have to reach a common velocity while forming a uniformly spaced string.Moreover,the final common velocity (reference velocity) is determined by the agents in a distributed and leaderless way.Then,the consensus protocol parameters are optimized for networks characterized by a communication topology described by a class of directed graphs having a directed spanning tree,in order to maximize the convergence rate and avoid oscillations.The advantages of the optimized consensus protocol are enlightened by some simulation results and comparison with a protocol proposed in the related literature.The presented protocol can be applied to coordinate agents such as mobile robots,automated guided vehicles (AGVs)and autonomous vehicles that have to move with the same velocity and a common inter-space gap.
I.INTRODUCTION
THE distributed control problem of multi-agent networks received tremendous attention in the last decades due to its applications in different areas [1].Each agent is a dynamical system and the problem of reaching an agreement on all or some components of the agents’ status is known asconsensusproblem.The consensus problem for first-order multi-agent systems has been largely studied considering different aspects:switching topology and time-delays [2]–[4];nonuniform time-varying delays [5];diverse time-delays and jointly-connected topologies [6];stabilization problem with time delay controlled by a distributed PID regulator [7];leaderless and leader-following consensus [8].
Moreover,several types of nonlinear vehicle dynamics can not be feedback linearized into single-,but into doubleintegrators and third order multiagent systems [9].Therefore,formal analysis of consensus problems for second-order systems are provided by [10]–[16].In particular,[15] demonstrates that the real and imaginary parts of the eigenvalues of the Laplacian matrix of the corresponding network play key roles in reaching consensus.In addition,in systems modeled by double-integrator dynamics,[16] investigates two kinds of different consensus strategies for multi-vehicle systems with a time-varying reference velocity under a directed communication topology.In [17],the authors study a decentralized control action for platooning maneuvers in vehicular networks embedding the spacing policy information as well as all the time-varying communication delays.Recently,a more general class of high-power multi-agent systems described by an extension of second-order nonlinear models are studied in [18]and [19].Consensus and distributed control of multi-agent systems also find applications in combination with adaptive neural networks,as shown in [20] where the authors simultaneously guarantee practical finite-time stability and asymptotic convergence.
In the literature,both the leaderless consensus and the leader-following consensus problems have been studied depending on whether or not there is a virtual leader specifying the global information [21].More precisely,in a leaderless consensus problem,there does not exist a virtual leader,while in a leader-following consensus problem,there exists a virtual leader that specifies the objective for the whole group [8].For example,the authors of [21] study a leaderfollower consensus problem for a set of agents subject to control input saturation.In addition,[22] considers a distributed leader-following consensus for second-order multiagent systems with nonconvex velocity and control input constraints.On the contrary,a leader is not required in the approach proposed by [23],but it is mandatory that at least one agent of the network knows the reference velocity.For a leader-following multi-agent system,[24] studies the consensus control of such systems with heterogeneous disturbances generated by the Brownian motion,developing an adaptive protocol based on Riccati inequalities.In addition,[25] integrates the distributed sliding-mode control algorithm to investigate the tracking control issue for second-order leader–follower multi-agent systems subject to nonlinearities.
Some advantages of leaderless consensus with respect to the leader-following approach have been enlightened in the related literature.In particular,leaderless consensus typically scales better and is more fault-tolerant than leader-following consensus [26].Moreover,the presence of leaders also decreases the degree of autonomy of the network [27],since the leaders generate global desired trajectories of agents,whereas in many practical missions,the agents need to reach autonomous agreement on an a priori unknown quantity.
Furthermore,an important problem concerning consensus algorithms is their convergence speed in order to implement them in real applications.In linear systems,a measure of the convergence speed is the smallest non-zero real part (for the continuous-time case) or magnitude (for the discrete-time case) of the system eigenvalues.Some efforts in this field are performed also in [28]–[33].The authors of [28] propose an iterative algorithm for maximizing the second smallest eigenvalue of a state-dependent graph Laplacian.In [29] and[30],communication time delay is considered in the optimal consensus problem.Furthermore,[31] provides a closed form for the optimal gains of some consensus protocols.Reference[32] is concerned with the consensus convergence rate for second order multi-agent systems:the fastest consensus convergence rate under the protocol is derived based on the assumption that all the eigenvalues of the Laplacian matrix are real.In [33],the explicit expression of the maximum convergence rate is established,and then,the effects of control parameters on the convergence rate are analyzed.
The convergence speed problems in discrete-time systems are recently analyzed in [34] and [35].In [34] the authors maximize the convergence speed of multi-agent systems with discrete-time double-integrator dynamics,optimally choosing the free parameters of the consensus protocol.The same authors in [35] optimize the consensus protocol speed subject to a lower bound on damping.
The aim of this paper is studying a consensus protocol to be applied by a leaderless network of autonomous agents that have to reach a common velocity while forming a uniformly spaced string.In addition,the paper objective is optimizing the protocol parameters to maximize the convergence speed by avoiding oscillations.This paper starts from existing second order consensus protocols,for instance proposed in[14],[32],[36],and it considers a protocol to be applied by a leaderless network of autonomous agents that have to reach a common velocity while forming a uniformly spaced string.More precisely,the value of the final common velocity(reference velocity) is decided by the agents through the consensus protocol,starting from an initial desired value for each agent.Furthermore,the agents communicate in a communication network described by a directed graph(digraph) having a directed spanning tree.We propose and prove the conditions that the consensus parameters have to satisfy to guarantee the asymptotic stability of the multi-agent system dynamics.Then,we show that the consensus protocol parameters can be optimized in order to maximize the convergence speed and avoid oscillations,if the network topology is described by a class of connected digraphs.
Hence,the new contributions of the paper are described in the following.
1) We propose and prove the conditions that the two protocol parameters and the communication topology have to satisfy in order to ensure that the proposed second order consensus is achieved in the multi-agent system.
2) We optimize the protocol parameters to obtain the fastest convergence avoiding oscillations for a class of connected digraphs having a directed spanning tree.To the best of our knowledge,few authors deal with the problem of the maximum convergence rate.However,the contributions of[31]–[33] optimize the convergence by using only one protocol parameter,while we solve the more complex problem involving two protocol parameters.
3) The optimal values of the parameters to maximize the convergence speed require that the communication topology has a directed spanning tree and symmetric strong components.This new result is not presented in the related literature.Moreover,we characterize the digraphs having a Laplacian matrix whose eigenvalues are all real.Indeed,the works of[31]–[33] introduce the assumption of real eigenvalues considering indirect graphs or without providing conditions of the topology for digraphs.
In order to enlighten the advantages of the proposed optimized consensus protocol,simulation results are presented and a comparison with respect to the approaches described in[31]–[33] is analyzed.
Finally,regarding the possible applications of the proposed leaderless consensus protocol,we remark it can be applied to coordinate moving agents such as mobile robots,automated guided vehicles (AGVs) and autonomous vehicles,also in emergency situations.Indeed,these agents have to converge to the average of their desired velocities,while forming a uniformly spaced string.For example,the algorithm can be implemented by automated vehicles on highways,in foggy conditions,to stay uniformly spaced with a constant velocity that tries to satisfy the driver’s preferences [37].In other words,a virtual safety car concept can be implemented,without the presence of a leader that is difficult to be elected in emergency situations.
The remainder of this paper is organized as follows.Section II describes preliminary definitions and the problem formulation.Section III proposes the protocol and proves the conditions that the protocol parameters have to satisfy in order to ensure that the multi-agent system control is asymptotically stable.Section IV proposes a criterion for choosing the protocol parameters to optimize the convergence speed and Section V provides numerical results to validate the proposed method.Finally,Section VI draws the conclusions.
II.PRELIMINARIES AND PROBLEM FORMULATION
A.Preliminary About Graph Theory
In this section,some basic concepts about graph theory are introduced [38],[39].
The communication topology of the group of agents is described by a directed graph (digraph) G=(V,E) that consists of a set ofnvertices V={1,...,n} connected by a set of edges E ⊆V×V.In this context,each vertex represents an agent and each directed edge represents the information exchange between two agents:(i,j)∈E if agentjcan receive information from agenti,whereiandjare called child and parent vertices,respectively.Adirected pathfrom vertexjto vertex vertexiin G is a sequence of edges(i,i1),(i1,i2),...,(il,j) in the digraph with distinct verticesik,k=1,2,...,l.A rootris a vertex having the property that for each vertexidifferent fromr,there is a directed path fromrtoi.Adirected treeis a digraph in which there is exactly one root and each vertex except for the root has exactly one parent.Adirected spanning treeis a directed tree,which consists of all the vertices and some edges in G.
We denote the neighborhood of vertexiby N(i),i.e.,N(i)={j∈V:(i,j)∈E}.The adjacency matrix of a graph is then×nmatrix A=[ai,j],defined such thatai,j=1 ifj∈N(i),andai,j=0 otherwise.A fundamental matrix that can be associated to a graph is the Laplacian matrix L=[li,j],which is ann×nmatrix that can be derived from the adjacency matrix.Its elements are defined asandli,j=−ai,j,i≠j.A property of L is L1n=0n,where0nand 1ndenote then-dimensional column vectors of all 0’s and 1’s,respectively.Hence,µ0=0 is an eigenvalue of L and1nis an associated right eigenvector.Moreover,letξindicate the corresponding left eigenvector,chosen so that ξT1n=1.
Now,the following result is recalled.
Lemma 1 [15]:The Laplacian matrix L has a simple eigenvalue µ0=0 and all the other eigenvalues have positive real parts if and only if digraph G has a directed spanning tree.
A digraph G is saidstrongly connectedif for any two verticesiandjthere is an oriented path fromitoj.
A strongly connected component of a digraph G is a subdigraph of G that is strongly connected and is maximal with this property.The collection of strongly connected components forms a partition of the set of vertices of G.Moreover,we saidsymmetrica strongly connected component characterized by a symmetric Laplacian matrix.
The following remark is introduced in order to characterize the structure of the Laplacian matrix in relation with the strongly connected components of a digraph [39].
Remark 1:Once the vertices of G are partitioned in strongly connected components,the corresponding adjacency matrix and Laplacian matrix can be put intocanonical formby relabelling the rows and the columns in a specific manner[39].The general version of the canonical form for a digraph partitioned inzstrongly connected components is the following:
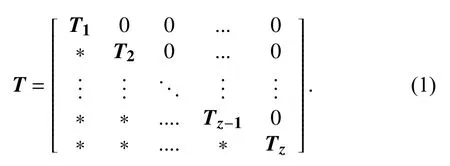
It is clear that the canonical form consists of square diagonal blocks corresponding to the connections within strongly connected components,zero to the right of these diagonal blocks and some elements zero or non-zero (denoted by “*”)to the left of each diagonal block.
B.Mathematical Tools
LetH∈R(n−1)×ndenote the following difference matrix:

Hhas full row-rank,so its (right) Moore-Penrose inverse can be computed asH+=HT(HHT)−1.Moreover,one can

C.Problem Statement
The dynamics of agentifori=1,2,...,nis described by a second-order system wherexidenotes the position of the agent,viits velocity anduithe control input
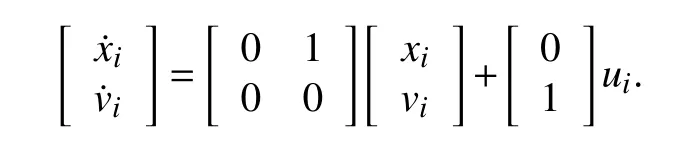
Moreover,the positions,velocities,and inputs of the multiagent system are denoted by then-dimensional vectorsx,v,andu,respectively.
Thus,the multi-agent system dynamics can be written as
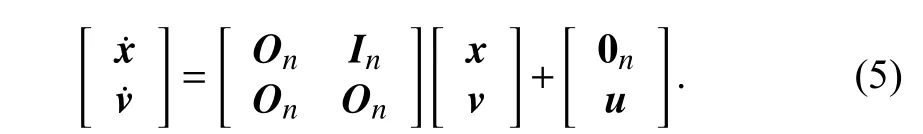
Multi-Agent System Control Problem:The multi-agent system control problem is to attain the following behaviour of the agent dynamics:i) Each agent must reach and steadily keep a common reference velocity;ii) All the agents must be spaced with uniform interspace gap.
Denoting byd(t)=Hx(t)∈R(n−1)the inter-agent distance vector,the objective of the multi-agent system control problem can be formally denoted as follows:
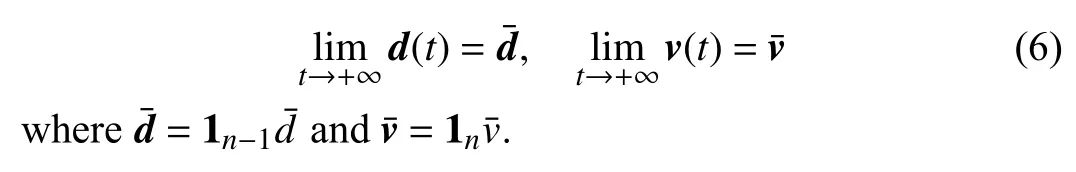
III.MULTI-AGENT SYSTEM CONSENSUS PROTOCOL
In this section we present the second order consensus protocol and prove the conditions that the protocol parameters and the communication topology have to satisfy in order to ensure that the consensus in the multi-agent system is achieved.
A.The Consensus Protocol
The multi-agent system control problem is solved by a consensus algorithm.In particular,if the communication topology of the agents group is described by G,uexplicitly depends on Lxand Lv,which in the literature is known asrelative feedback[40].Moreover,each agent can include its own velocity value in the control law:this is known in the literature asabsolute feedback[40].
We assume the common reference velocity that each agent has to reach is unknown to the agents.More precisely,each agentistarts from an initial valueyi(0) fori=1,...,nof the reference velocity and by the following consensus protocol the agents reach a common value of the reference velocityyifori=1,...,n:
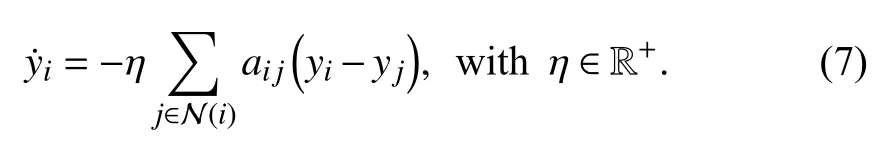
Now,the following consensus algorithm is proposed:
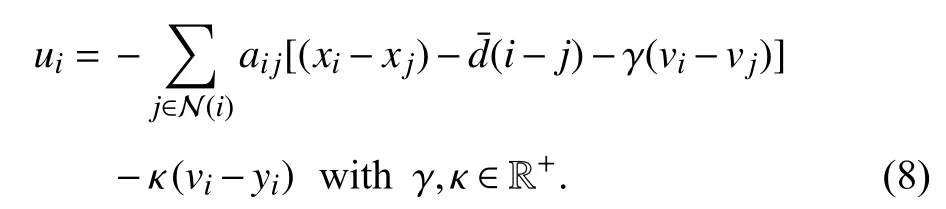
In other words,by using (8),each agent can communicate its own velocity and the relative distance with its neighbours,such an assumption is very common in the related literature[16],[34]–[36].Assuming that each agent has to reach a common reference velocityand the same inter-space,the rationality of algorithm (8) is the following:by the first terms each agent communicates the actual distance from its neighbour and the objective inter-space to be imposed between two nearby agents;analogously by the second terms the agents communicate the actual difference between the velocities of its neighbours and the reference velocity.Parametersγandκdetermine the weights given to the relative and absolute velocity feedbacks,respectively,with respect to the distance (relative) feedback.In other words,with a higher value ofγ,the control puts more weight on the global error.Instead,with a higher value ofκeach agent becomes more“selfish”,giving its absolute velocity error more importance.
Protocol (8) makesyifori=1,...,nconverge to a common value,which depends on the communication topology and initial valuesyi(0).This avoids the need for a leader and is independent of the initial velocitiesvi(0).

and (7) becomes

Substituting (9) in (5) and adding (10) in the state equations(5),the dynamics of the multi-agent system is the following:
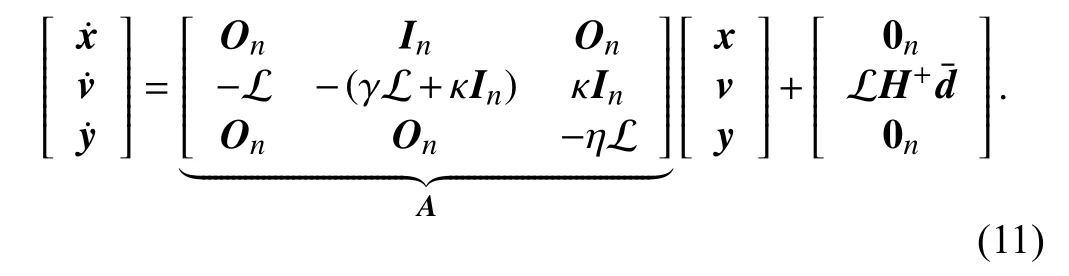
MatrixAcan be partitioned as follows:
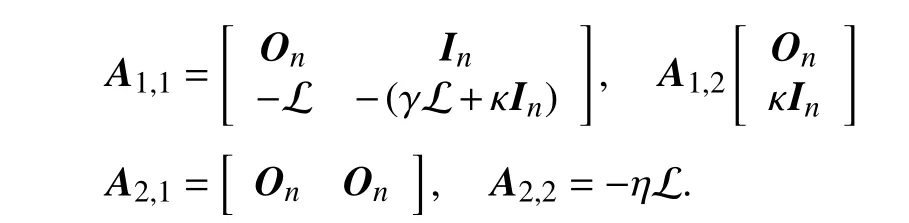
The spectrum ofAis the union of the spectra of matricesA1,1andA2,2.As it is shown in [41],the characteristic polynomial ofA1,1is the following:
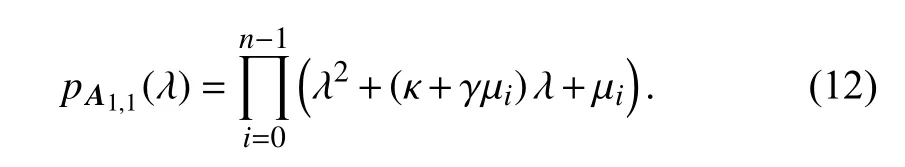
Moreover,the characteristic polynomial ofA2,2is
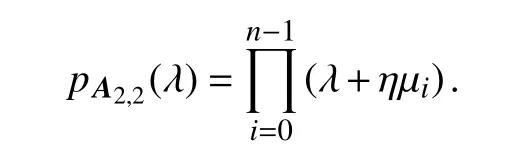
The eigenvalues ofA1,1are
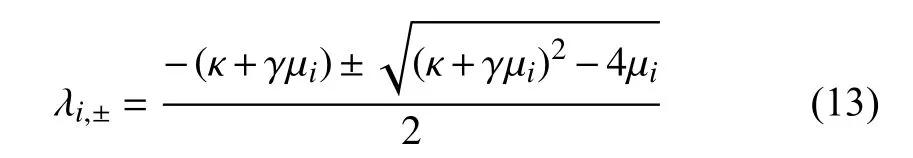
fori=0,...,n−1.
Note that theydynamics is independent of the dynamics of the rest of the multiagent system and the convergence value is
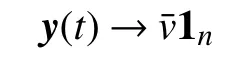
B.Multi-Agent System Control Problem
In order to solve the multi-agent system control problem,a change of variables of system (11) is performed as it is described by the following proposition.
Proposition 2:Let us define the new variablesp=Hx−=v−yandr=Hy.Then,the dynamics of system (11) can be described by the following equation:
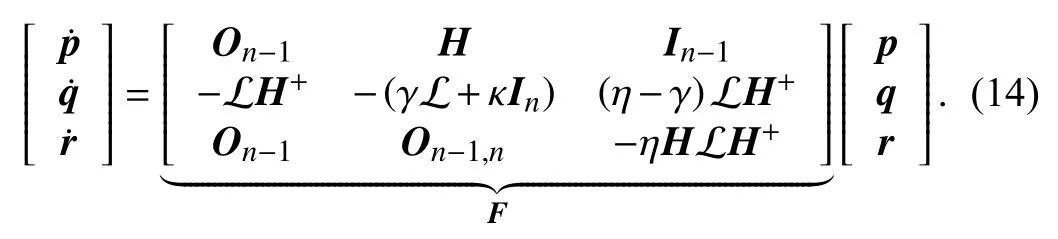
Proof:We define the following new variables:
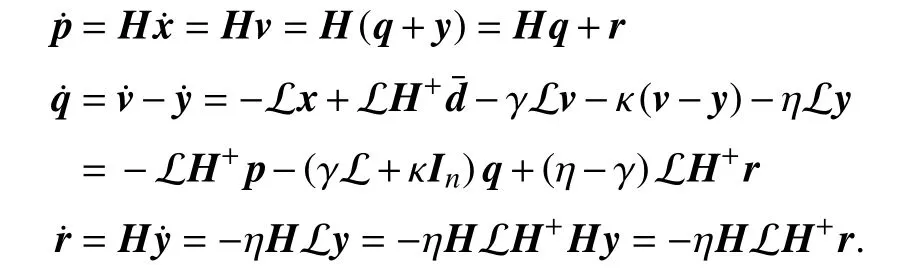
Equation (14) describing the system follows.
Note that the multi-agent system control problem (6) is equivalent to making system (14) asymptotically stable.
Let us partitionFinto the following 4 blocks:
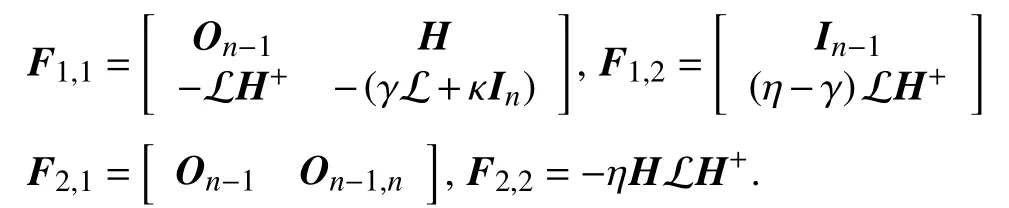
Now we prove that the spectrum ofFis the union of the spectra ofF1,1andF2,2and we show that it coincides with the spectrum ofA,up to the two null eigenvalues.
Lemma 2:The eigenvalues of matrixFare the roots of
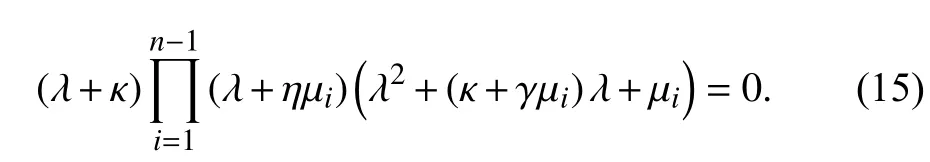
Proof:Let us start with the determination of the characteristic equation ofF2,2.We transform matrix L to its Jordan canonical form by ponting out the null eigenvalue and the corresponding eigenvectors

Since L has at least one null eigenvalue,i.e.,µ0=0,from(16) and(19)equation(15)follows.
Remark 2:By Lemma 1,if digraph G has a directed spanning tree,thenF1,1has one eigenvalue λ0=−κ and the other 2n−2 eigenvalues are given by (13).
Now,we prove the conditions thatγandκmust satisfy in order to ensure that system (14) is asymptotically stable,so that protocol (9) successfully solves the multi-agent system control problem.
Theorem 1:Consider a set of agents that communicate in a network topology described by a digraph G that has a directed spanning tree.The dynamics of the multi-agent system (14) is asymptotically stable if and only if it holds
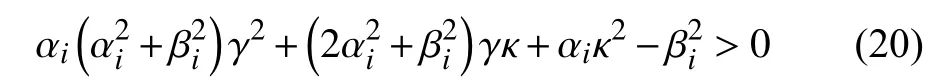
fori=1,...,n−1,with αi=R[µi] and βi=I[µi] (R [c] and I[c]) denote the real and imaginary parts of complex numberc,respectively).
Proof (Only if):Let us consider the factors of (15).If G has a directed spanning tree,then according to Remark 2 it holds R[λ]=−R[ηµi]<0∀i=1,...,n−1.Moreover,let us consider the remaining factors of (15)
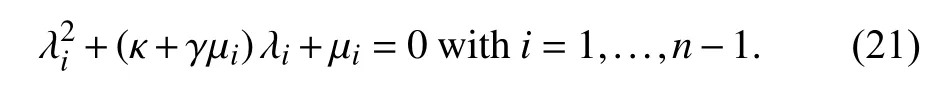
Using the Routh-Hurwitz criterion for second-order polynomial with complex coefficients,we have that matrixFis Hurwitz-stable if and only if
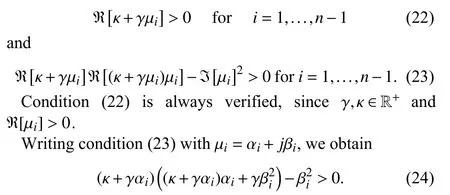
After some calculations,result (20) follows from (24).
Proof (If):Let us assume that (20) is verified,then (24),(23),(22) follow.Hence,by the Routh-Hurwitz criterion equation (21)is Hurwitz-stable and system (14) is asymptotically stable.
Let us consider the (γ,κ) plane:Each inequality of (20)defines a region of stability in the plane,limited by a hyperbola.More precisely,in order to obtain stability,the point (γ,κ) must lie beyond a set of “critical hyperbolae”,where thei-th hyperbola depends only on µi.Fig.1 shows the stable and unstable regions of the (γ,κ) plane that such inequality produces.
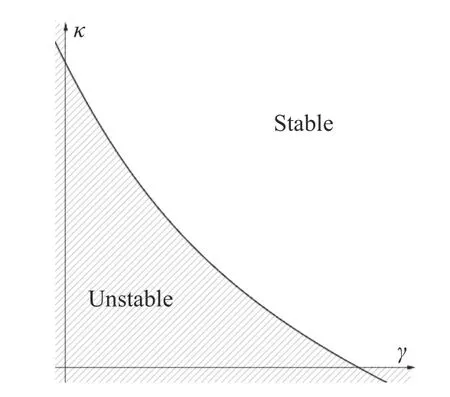
Fig.1.A critical hyperbola in the (γ,κ) plane.
Theorem 1 generalizes the stability conditions presented in the related literature [17],[32] and [33] that consider κ=0.Indeed,if γ=0 (no relative feedback on velocity control),(20) becomes[17].Moreover,if κ=0 (no absolute feedback on velocity control),we get[32],[33].
Now the following corollary characterizes the digraphs having the Laplacian matrix exhibiting real eigenvalues.
Corollary 1:If all the strongly connected components of digraph G are symmetric and G has a directed spanning tree,then L of G has a simple eigenvalue µ0=0 and the other ones are real:in such a case (20) is verified ∀ γ,κ ∈R+.
Proof:According to Remark 1,the Laplacian matrix ofG can be put into canonical form (1) and the eigenvalues ofL are the eigenvalues of the diagonal blocks of L associated to each strongly connected components of
G.Now if such Laplacian diagonal blocks are symmetric,then the eigenvalues of each block are real.Hence,we can conclude that if all the strongly connected components of digraph G are symmetric and G has a directed spanning tree,then L of G has a simple eigenvalue µ0=0,the other ones are real and (20) is verified∀γ,κ ∈R+.
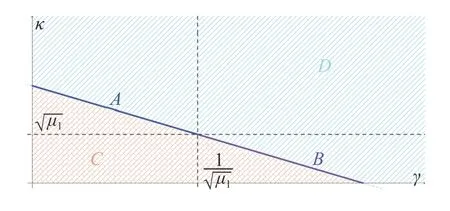
Finally,we enlighten that no constraint on the parameterηis necessary for stability.However,a possible choice could be selectingηsuch that − R[ηµi] In this section the eigenvalues of matrixFare optimized by choosing parametersγandκin order to maximize the convergence speed and avoid large oscillations. To this aim we assume that the communication digraph G is characterized by a Laplacian matrix with eigenvalues such that:µ0=0 and µi∈R+fori=1,...,n−1 arranged in increasing order withi.This condition is satisfied by the network topologies described by indirect graphs or the class of digraphs specified by Corollary 1. The objectives of the eigenvalue allocation problem are: i) Avoiding large oscillations and speeding up the convergence by selecting a real dominant eigenvalue and maximizing the its absolute value; ii) Allocating the non-dominant eigenvalues as far away as possible from the imaginary axis. Moreover,let us introduce the set of eigenvalues with minimum absolute real part for given values ofγandκ and the set of the remaining eigenvalues Now,a second function is defined as follows: Problems i) and ii) can be formally defined by the following optimization problems P1 and P2,respectively: P1) m axγ,κ∈R+f1(γ,κ),s.t.=0; P2) m axγ,κ∈R+f2(γ,κ). The following proposition provides a solution of problems P1 and P2 in closed form. Proposition 3:Consider a set of agents that communicate in a network topology described by a digraph G that has a directed spanning tree and all the strongly connected components symmetric.Let µ0=0 and µi∈R+fori=1,...,n−1 be the eigenvalues of the Laplacian matrix ofG arranged in increasing order withi.Then the eigenvalues of the controlled system (14) that solve P1 and P2 are obtained by the following values ofγ,κandη: Proof:The proof is in the Appendix. In this section we provide numerical results and comparisons to show the performance of the proposed consensus protocol.We assume that the agents communicate by the topology GP(Fig.2) that is characteristic of a group of agents that have to move in a chain and do not include a leader.By Theorem 4 of [42],the real eigenvalues of the corresponding Laplacian matrix are the following: We test a scenario ofn=8 agents that can be robots or AGVs in industrial environments.The agents queue up to each other with the initial conditions reported in Table I that shows the initial inter-agent distance vectord(0) (in metres),the initial velocitiesv(0) (in m/s),the initial reference velocitiesy(0) (in m/s) (selected higher than the initial velocities),the fixed distance(in metres) and the values of the selected parametersandchosen according to (25) with Fig.2.Communication digraph G P. TABLE IINITIAL CONDITIONS OF THE TESTED SCENARIO AND PARAMETERS The simulation outputs are reported in Figs.3 and 4,showing the position and velocity trends over time,respectively. Fig.3.Positions over time for the network topology G P. Fig.4.Velocities over time for the network topology G P. In addition,let us consider the communication topologyobtained from GPof Fig.2 where two connections are dropped as shown in Fig.5.It is apparent thathas a directed spanning tree and symmetric strongly connected components.Hence,according to Corollary 1 and Proposition 3 the eigenvalues of L are real and the values of=1.1355,=0.6652 andare chosen according to (25).The results of the simulation are reported in Figs.6 and 7,showing how the agents reach the convergence values of positions and velocities,respectively. Fig.5.Communication digraph . In order to show how the proposed consensus protocol works in situations where an increasing number of communication links are disconnected,we consider the communication topologiesshown in Figs.8 and 9,respectively.The obtained digraphs have a directed spanning tree and symmetric strongly connected components.If the values of the parameters are selected according to (25) (i.e.,=0.7429,=0.7429 for the digraph of Fig.8 and=0.8944,=0.8944for the digraph of Fig.9),the velocity behaviours resulting from the simulations are reported in Figs.10 and 11,showing that the agents reach the consensus with similar convergence speeds. Fig.6.Positions over time for the network topology Fig.7.Velocities over time for the network topology. Fig.8.Communication digraph . Fig.9.Communication digraph In this subsection we compare the proposed protocol with a similar method presented in the related literature.In particular,we consider the protocols proposed in [32] and [33] that are applied to undirected graph topologies characterized by Laplacian matrices with real non-negative eigenvalues µifori=0,...,(n−1) Fig.10.Velocities over time for the network topology Fig.11.Velocities over time for the network topology being ‖(·)‖ the 2-norm of vector (·) andtheconvergence speed value of the two protocols.We uset0.5%as performance index,defined by TABLE IIINITIAL CONDITIONS OF TESTED SCENARIOS FOR THE COMPARISON We run 1 000 cases for each of the two algorithms and averaged out the results.By applying protocol (9),we obtain and by applying (27) the performance index is The benefits of the proposed protocol with respect to the similar protocol (27) are apparent:i) Improved convergence speed;ii) Possibility of reaching a common reference velocity and a consensus of the value of the common velocity;iii)Possibility of reaching the uniform inter-space gap. This paper considers a leaderless consensus protocol that a multi-agent system can apply in order to reach a common velocity while forming a uniformly spaced string.The leaderless agents are able also to reach a consensus about the value of the common final velocity (reference velocity) by starting from an initial desired value for each agent.We prove the conditions that guarantee the consensus control rules allow the agents stably to achieve the decided inter-vehicular distance and the common velocity.Moreover,the optimal eigenvalues allocation is obtained in a closed form of the control parameter values for a class of digraphs having a directed spanning tree and modelling the communication network topology. The advantage of the method is that a leader is not required and by the optimized protocol parameters the fastest rate of convergence avoiding oscillations is guaranteed.However,the optimization of control parameter values depends on the communication graph topology:if the topology changes,the parameters must be updated by calculating the eigenvalues of the Laplacian matrix. Future research directions will focus about the assessment of the protocol in presence of constraints on agent velocities and accelerations.Moreover,investigations about the impact on the stability and convergence of the delays of communication will be analyzed.To this aim suitable conditions will be sought to guarantee correct behaviour and good performance of the protocol. APPENDIx PROOF OF PROPOSITION 3 Proof:Let us consider the eigenvalues of the submatrixF1,1.Taking into account (13),one has Fig.12.The (γ,κ)-plane divided into 4 regions. Then,we determine or bound the value of the objective functionf1in each region. RegionAis the segment defined by (30) and proving the proposition.IV.EIGENVALUE ALLOCATION FOR THE CONTROLLED MULTIAGENT SYSTEM
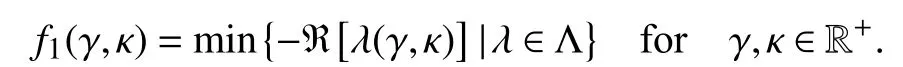
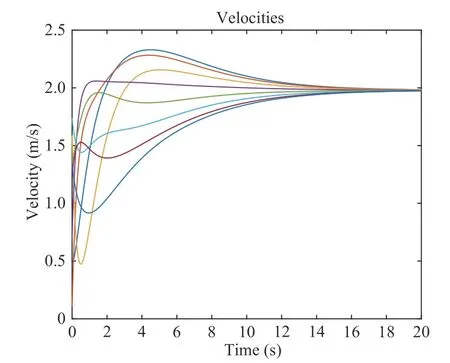
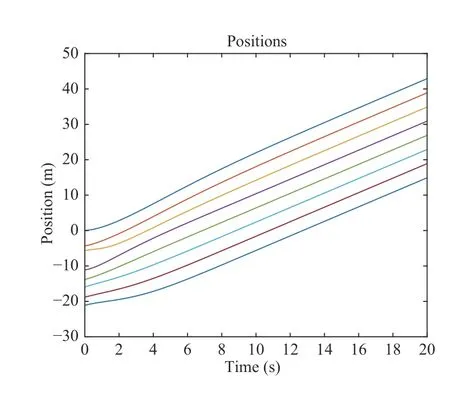
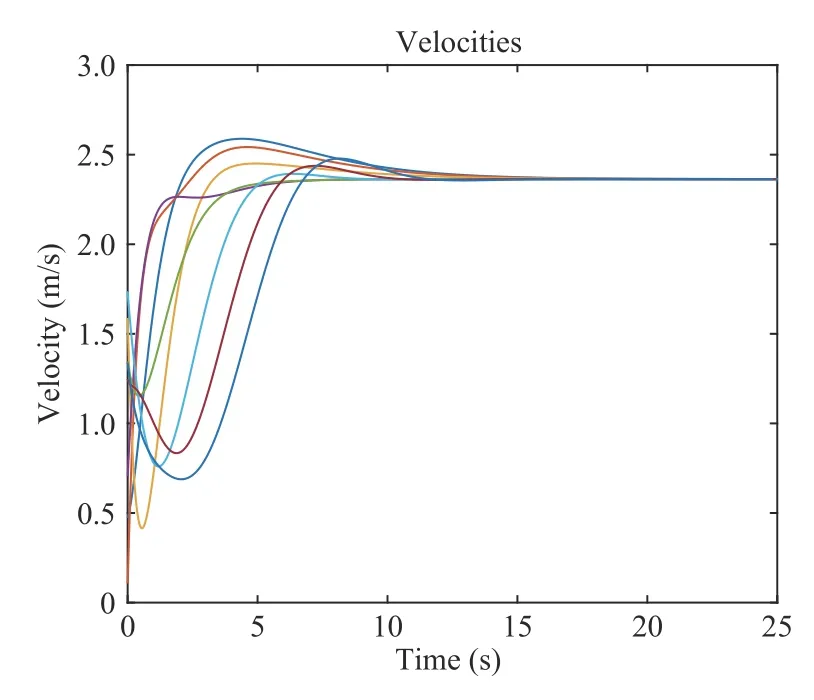
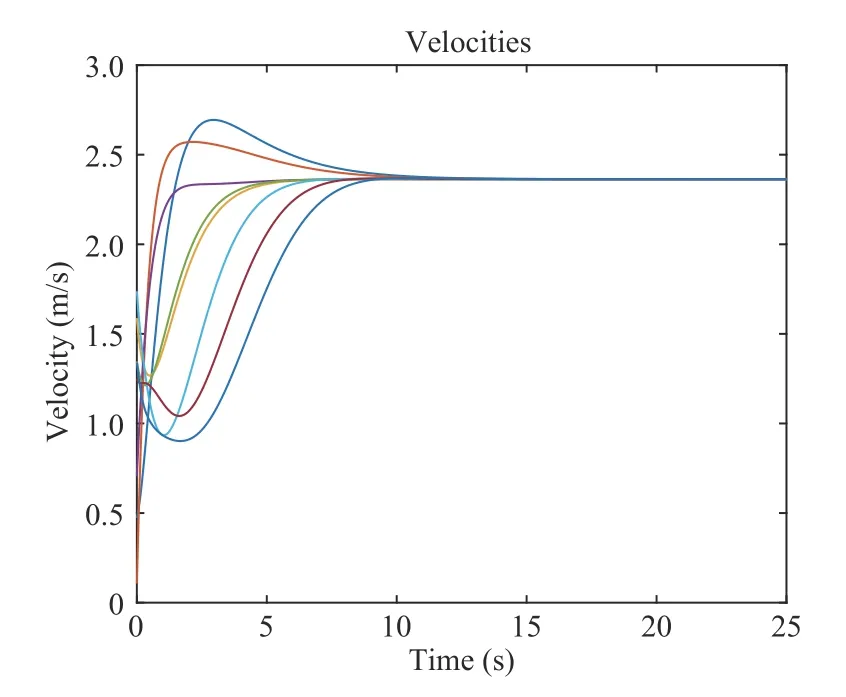
V.NUMERICAL RESULTS AND COMPARISONS
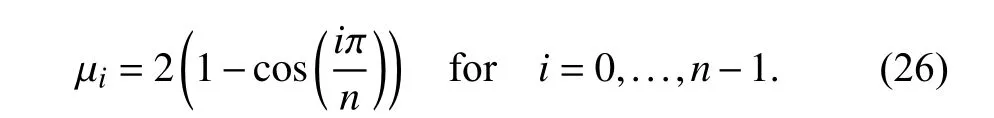
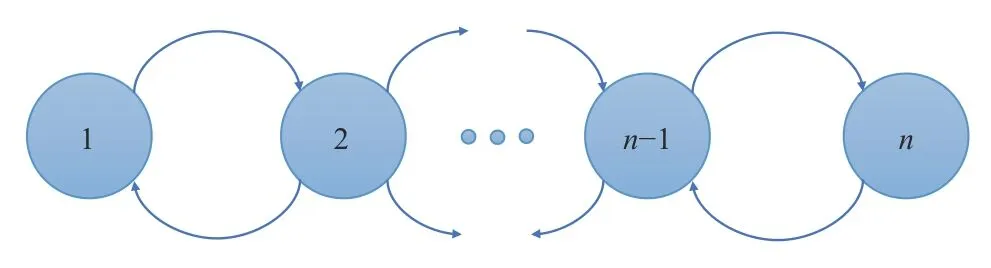
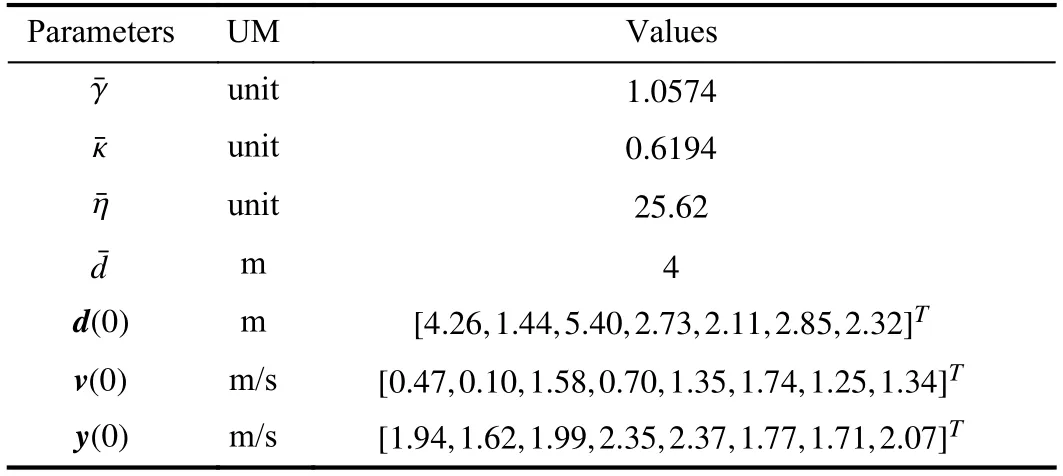
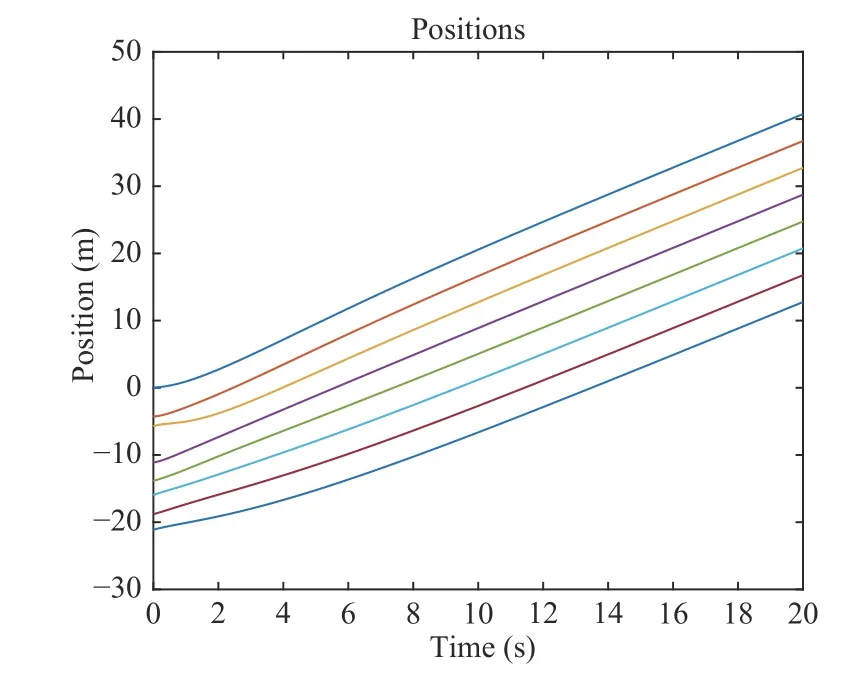

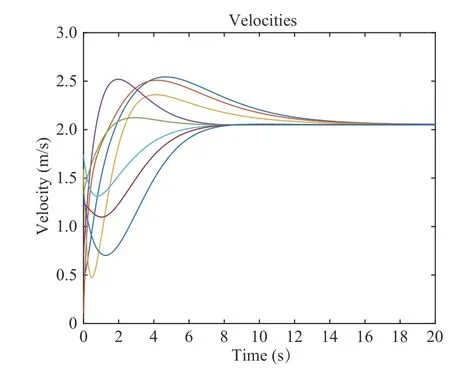


A.Some Comparisons
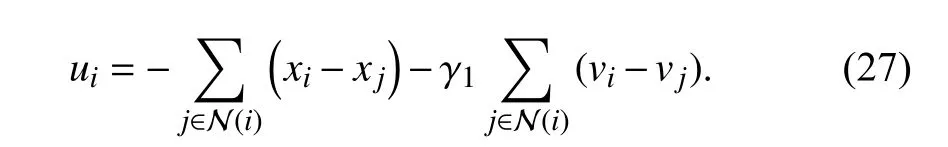


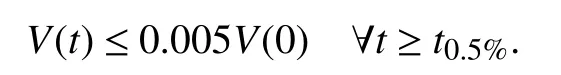
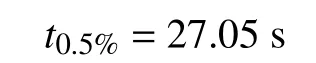
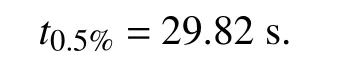
VI.CONCLUSIONS
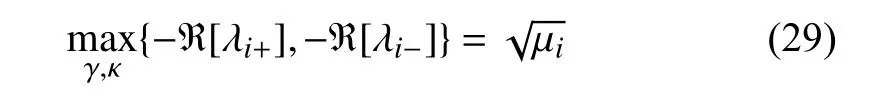



杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Sampling Methods for Efficient Training of Graph Convolutional Networks:A Survey
- Fault Accommodation for a Class of Nonlinear Uncertain Systems With Event-Triggered Input
- Precise Agriculture:Effective Deep Learning Strategies to Detect Pest Insects
- Exponential Set-Point Stabilization of Underactuated Vehicles Moving in Three-Dimensional Space
- An Adaptive Rapidly-Exploring Random Tree
- Aerodynamic Effects Compensation on Multi-Rotor UAVs Based on a Neural Network Control Allocation Approach
