An Adaptive Rapidly-Exploring Random Tree

Binghui Li and Badong Chen,

Abstract—Sampling-based planning algorithms play an important role in high degree-of-freedom motion planning (MP)problems,in which rapidly-exploring random tree (RRT) and the faster bidirectional RRT (named RRT-Connect) algorithms have achieved good results in many planning tasks.However,sampling-based methods have the inherent defect of having difficultly in solving planning problems with narrow passages.Therefore,several algorithms have been proposed to overcome these drawbacks.As one of the improved algorithms,Rapidlyexploring random vines (RRV) can achieve better results,but it may perform worse in cluttered environments and has a certain environmental selectivity.In this paper,we present a new improved planning method based on RRT-Connect and RRV,named adaptive RRT-Connect (ARRT-Connect),which deals well with the narrow passage environments while retaining the ability of RRT algorithms to plan paths in other environments.The proposed planner is shown to be adaptable to a variety of environments and can accomplish path planning in a short time.

I.INTRODUCTION

AS a class of motion planning algorithms,sampling-based planning methods represented by probabilistic road map(PRM) [1] and rapidly-exploring random tree (RRT) [2] have achieved a lot of results in practical planning.Among them,algorithms based on RRT have been widely used in robotic arm path planning,unmanned aerial vehicle (UAV) motion planning and other robot motion planning problems [3]–[6].These kinds of algorithms can not only solve highdimensional planning problems which are difficult to be solved by deterministic methods,but also solve motion planning problems with differential constraints.The basic feature of sampling-based planning algorithms is to extract spatial information by sampling in an unknown space with a sampler.As the number of sampling points increases,the structure of the unknown space can be described at a higher resolution,making it possible to quickly find a path connecting two state points that meets the constraints.As an important sampling-based algorithm,RRT is based on the incremental growth of the search tree to explore the spatial state.In the planning process of RRT,after each sampling,the nearest neighbor to the sampling point in the tree will grow towards the sampling point.Since the sampling points are evenly distributed in space,the tree can gradually fill the space with the sampling process until the end of the planning.

Due to the probability characteristics of the sampler,the RRT algorithm has different results for different runs of the same task.Moreover,because it is not easy to sample in a narrow region,the number of sampling points in the narrow region is generally small.As a result,the planner cannot find the narrow passage quickly and pass through it.The randomness of RRT planning results has little effect on tasks that only need to quickly find a feasible path.However,the lack of planning capabilities for narrow passages limits the application of such algorithms in difficult environments.Because of this defect,some improved RRT algorithms have been proposed,among which rapidly-exploring random vines(RRV) [7] can achieve good results by using principal component analysis (PCA) to determine the type of local environments to increase the number of sampling points in the narrow passages.However,compared with RRT,RRV’s planning time for cluttered environments may increase significantly,showing that the performance of RRV has environmental dependence.

In this paper,we propose a new improved algorithm called adaptive RRT-Connect (ARRT-Connect),which is based on the improvement of RRV and a faster bidirectional RRT named RRT-Connect [8].Specifically,the new algorithm includes the following new features.First,a new sampler is designed for the sampling process,which is more greedy in sampling behavior.At the beginning of the planning process,the search tree will be expanded to explore the space as much as possible,thus speeding up the planning.Second,ARRTConnect simplifies the process of judging the type of local environments,which allows the new algorithm to capture the positional relationship between sampling points and narrow passages with only a few simple calculations,and retain the ability to perform well in planning tasks with narrow passages.Finally,ARRT-Connect uses bidirectional search like RRT-Connect.To overcome the performance instability caused by greedy bidirectional search,we modify the exchange strategy of bidirectional search,so that ARRTConnect can better complete various planning tasks and further shorten the planning time.The proposed algorithm can achieve good results in most environments,which can not only handle planning tasks with narrow regions but also retain planning abilities for general environments.

II.RELATED WORKS

To deal with the problem where the RRT algorithm is inherently inadequate in planning for difficult environments with narrow regions,many improved algorithms have been proposed.These algorithms can be divided into algorithms based on improved sampling distribution and algorithms based on improved tree extension.

The algorithms based on improved sampling distribution aim to increase the number of sampling points in difficult regions such as narrow passages by changing the distribution of sampling points and increasing the probability of passing through narrow regions.In [9],the authors use bridge-test to increase the sampling points in the narrow passages while reducing the points in the non-interested areas,so that the planner’s exploration opportunities for narrow passages increase.In [10],the authors add a radius for each node in the tree to indicate that the region around the node is a free area that can be sampled.If an obstacle is encountered in the expansion process of a node in the tree,the radius of the node will be updated.This method increases the number of valid sampling points and improves the planning ability for the bug environment.In [11],the authors add a parameter to describe the density of surrounding points for each node of the tree.The sampler then collects new points around the lowest density point to expand the tree into unexplored areas.In [12],if there is an obstacle on the line between the sampling point and the nearest neighbor point in the tree,local optimization will be performed.First,the sampling point retreats to the boundary of the obstacle,and then the boundary point closest to the original sampling point is found.All the involved points are finally added to the tree in a normal manner to increase the probability of the tree entering the narrow passages.In [13],the authors change the sampling behavior by dividing the space into different regions.This method calculates the entropy of the sampling points and divides the space into the obstacle,free,boundary and difficulty areas according to the value of entropy.After that,the number of sampling points in the difficult area will be increased so that the planner can better deal with planning problems in a difficult area.In [14],the authors record a radius valueRfor each node in the tree,which means that the hypersphere with this node as the center andRas the radius is a free space.Moreover,only the sampling points outside the hypersphere are accepted by the planner,so the tree can be expanded to unexplored areas as much as possible.

The improved algorithms above achieve the desired performance in the face of an environment containing narrow passages.However,many algorithms introduce additional variables that need to be updated for each node in the tree,which will increase the amount of calculation after sampling.Furthermore,during the planning period,most of the planners are not aware of the spatial structure.Therefore,the drawback of the above algorithms is that it is unable to compute a more suitable expansion direction for the tree in difficult environments.

The algorithms based on the improved tree extension focus on the aspect of how to calculate an appropriate extension direction for the search tree to increase expansion ability in narrow passages.In [15],if a sampling point cannot connect to the search tree in the extension step,a local tree will be generated at the sampling point.The planner will then try to connect these trees.If a tree is in a narrow passage,the planning time of such difficult environments can be reduced.In [16],the planner uses the information of obstacles in the workspace to calculate the appropriate expansion direction.But a lot of calculations is needed to obtain the geometric information of obstacles.In [17],in view of a situation where the nodes in the tree are already in a narrow passage,the authors use PCA to calculate the extension direction for the tree,so that the tree can more easily pass through the narrow passage.However,it does not solve the problem of how the tree enters the narrow passage.In [18],the authors use bridgetest and PCA to find narrow passages,then adjust the direction of tree expansion.At the same time,to speed up the planning process,only the sampling points outside the free hypersphere area of each node are accepted by the planner.In[19],the authors propose a method to find narrow passages by clustering the sampling points.After clustering,a tree will be generated in each center and the reinforcement learning method will be used to expand these trees.In [20] and [21],the authors also use multiple local trees to adjust the global search state.Moreover,the authors in [21] try to use Bayesian estimation to adjust the local sampling direction to enhance the algorithm’s processing ability in difficult environments.These improved algorithms generally compute and select the appropriate tree extension direction according to the spatial information.However,most of these methods have high computational complexity and strong dependence on narrow environments.

The context-dependent algorithm [22] may solve the environmental dependency that appears in previously mentioned algorithms.Nevertheless,that algorithm is implemented by combining several methods.The algorithm proposed in this paper attempts to solve the problems of narrow passages and environmental adaptability in a simple process.

III.PROPOSED ALGORITHM

The algorithm proposed in this paper aims to improve the planning ability of traditional RRT algorithms for an environment containing narrow passages.Meanwhile,in order to reduce the planner’s dependence on such specific environments,the new algorithm retains the planning capabilities for common environments (e.g.,cluttered) as much as possible.The new algorithm modifies three important parts of RRT-Connect to achieve the desired performance.Details of the proposed algorithm are given below.

A.Algorithm Framework

The sampling space used in the proposed algorithm is the configuration space (C-space).The configuration space is a space composed of parameters describing the state of the robot.The states that the robot can reach form a free space,while the set of states that the robot can not reach or that the robot will collide with obstacles is obstacle space.The concept of configuration space has been widely used in various planning algorithms since it was proposed.Common configuration spaces include the space composed of joint variables of the manipulator,the space composed of the coordinates of the planar robot,etc.In the configuration space,the robot is simplified to a point,so no matter what kind of robot system,we are ultimately planning a path for a point in the space.If an algorithm can solve a certain configuration space planning problem,then the robot system similar to this configuration space can use this algorithm for motion planning.From another perspective,the configuration space is equivalent to a higher level of abstraction of the planning problem,which makes the planning algorithm separate from the specific robot system and allows for application in more motion planning problems.

The framework of the new algorithm is identical to RRTConnect in [8] and is shown in Algorithms 1 and 2.The modified parts are Random_Config,Extend and Swap respectively.First,we design a new sampler to get random configurations in the Random_Config function.The parameterR_Tis used to describe the size of the tree in C-space.ThePgoalandPoutsidecontrol the probability of the sampler sampling in different regions.Second,when the extension fails,we will determine the type of local environment to reboot the tree’s extension in the Extend function.Last,the density information of the tree is used to achieve a more flexible exchange in the Swap part.The complete description of these three modifications is given in subsequent sections.

B.Greedy Sampler

As the first step of the algorithm,the behavior of the sampler directly affects the exploration process and the final planning performance.The goal of the sampler proposed in this paper is to explore the space more quickly to shorten the overall planning time.In [23] and [24],the planners sample multiple points in each sampling process,then they select appropriate tree nodes and corresponding sampling points to expand the tree according to the established criteria.Essentially,these two methods reduce invalid sampling points and planning time by selecting as many unexplored areas as possible in the sampling process.The basic idea of the sampler used in ARRT-Connect is the same,but the acceleration is achieved by constantly changing the sampling area rather than adding additional sampling points.That means the sampler is limited to sample points in the selected unexplored region with a higher probability and the selected area may change in each sampling procedure.The details are shown in Algorithm 3.

In Algorithm 3,two parameters,PgoalandPoutside,divide[0,1] into three intervals,which in turn represent the sampling probability of the sampler in the target region,the unexplored region and the area within the tree.Sampling in these three different areas has different meanings.Goal-biased sampling can speed up the connection of the tree to the target point.Sampling in the unexplored area can accelerate the expansion of the tree,while the uniform sampling in the tree area can increase the spatial resolution of the explored region.The value ofPgoalis generally set to be relatively small and does not need to be changed in the whole process,while the value ofPoutsideis set to be larger at the beginning (e.g.,0.95).This is done to sample in the unexplored area as much as possible at the beginning.Afterwards,as the number of points increases during the process of the algorithm,the value ofPoutsidegradually decreases,so that the sampler tends to sample in the explored region.

If the target area is selected for sampling,the sampler returns the goal point as the sampling point directly.But,in the other two cases,the sampler needs to use the parameterR_Tto select the unexplored region or the region within the tree.R_Tis a parameter added to the search tree,which describes the minimum external hypercube of the tree,named the tree region.Therefore,the sampler sample uniformly in the region described byR_Tcan get a random point in the explored area (Lines 8−9 in Algorithm 3).R_Trecords the range of intervals the tree occupies in each dimension of the space.The original range of each dimension minus the interval ofR_Tin that dimension constitutes two independent unexplored intervals (Fig.1).These unexplored intervals are the basis for the sampler to select the sampling region.When the unexplored area is selected to be sampled (Lines 1 1−21 in Algorithm 3),the length of each unexplored interval dimension is first calculated,then the dimension with the longest unexplored interval will be recorded.After that,the sampler will select the recorded dimension with a probabilityPmax,wherePmaxis the ratio of the unexplored interval lengths of the recorded dimension to the sum of the unexplored interval lengths of all dimensions.Otherwise,it will choose one of the remaining dimensions that contain unexplored intervals.Finally,an unexplored region consisting of the full range of the remaining dimensions and the larger of the two unexplored intervals of the selected dimension is selected.The sampler will sample uniformly in this unexplored area to return a random point.In the whole sampling process,ifR_Toverlaps with the C-space,i.e.,the search tree touches all the boundaries of the configuration space,then the sampler will degenerate to global uniform sampling to increase the number of sampling points in the tree area.

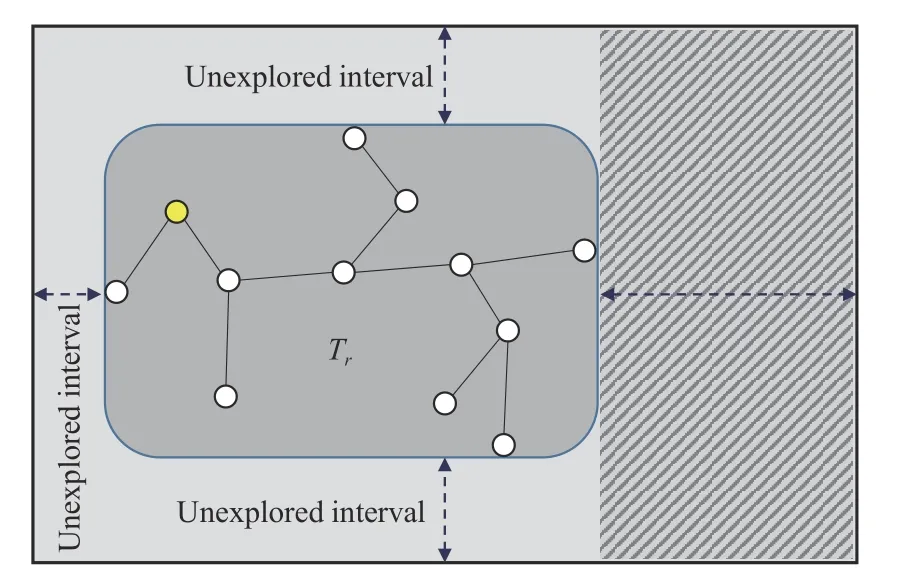
Fig.1.R _T divides the C-space into two regions:inside the tree and outside the tree,the sampler will sample in the unexplored regions with a higher probability.The shaded region on the right of the figure is one of the unexplored regions that might be selected.

Such a design enables the planner to rapidly expand the tree to all parts of the C-space in the early stage of the planning process,and then gradually increase the spatial resolution within the tree.Moreover,because of the rapid exploration of configuration space,this strategy also helps the planner to accomplish the planning tasks with fewer sampling points.

C.Environmental Judgment

After obtaining a sampling point from the sampler,the normal RRT-Connect extension method is first tried.If it fails,it indicates that there is an obstacle between the sampling point and the nearest point in the tree,then the environmental type judgment process is entered and an appropriate direction will be selected to retry the expansion operation.The whole process is summarized as Algorithm 4.

At the beginning of the environmental type judgment process,the planner needs to collect the local spatial information around theqnearthat failed to expand,which is accomplished by local sampling.In this paper,local sampling refers to selecting points at a certain distance from the center point along each dimensional axis.To obtain enough sampling points to describe the local structure,the planner selects the first batch of points withqnearas the center and then takes the first batch of sampling points as the center to obtain the second batch of points.Moreover,the expansion distance used in the second batch is smaller than that in the first batch to gain more proper points in local space.Fig.2 describes the entire procedure of local sampling.The advantage of this local sampling method is that the number of sampling points obtained by local sampling will automatically increase with an increase in spatial dimension,so it is unnecessary to artificially adjust the number of local sampling points every time the dimension changes.

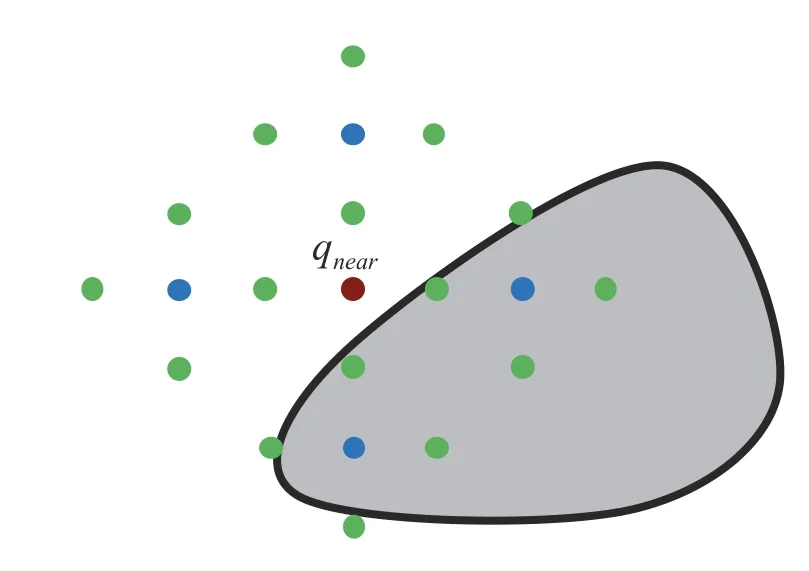
Fig.2.Process of local sampling.The red point q near represents the point in the tree that failed to expand,while the blue points and the green points respectively represent the first batch of local sampling points centered on qnearand the second batch of sampling points centered on the first batch of points.

After we get pointsSpointsin local sampling,we divide the points intoSobstacleandS freeaccording to whether the sampling point is located in free regions,then the mean pointaveobsof the non-free setSobstacleis calculated.Ifaveobsis in an obstacle region,it is considered to encounter a wall-type obstacle,after which the distance between any two points inSobstacleis calculated to get the two points farthest apart.The line of these two points is the new expansion direction.This direction generally represents the boundary direction of the wall,so the tree shows the characteristics of growing along the surface of the obstacles.However,ifaveobsis in free space,it is further judged whether the distance betweenqnearandaveobsis greater than δ,which is a threshold smaller than the extension step size.If it is,theqnearis considered to be outside a narrow passage,the search tree will try to expand towardsaveobs.Otherwise,qnearis likely to be located in a narrow passage after which the two points farthest apart inS freewill be calculated.The new expansion direction will be the connection direction of these two points.The tree will try to expand several times,which makes it easier for the tree to pass through the narrow passage.If one of them fails,the algorithm will immediately enter the final exchange process.Fig.3 shows the three scenarios.When using the above strategy to determine the type of local environment,concave obstacles may be judged as narrow passages,resulting in additional time consumption.However,as the extension fails,the algorithm will enter the exchange procedure immediately,so the algorithm will not spend too much time in the case of an incorrect judgment.

D.Bidirectional Exchange Strategy

The last step in each round of the algorithm is to select one of the search trees to expand in the next iteration according to the policy.In general bidirectional search,whether two trees need to exchange depends on the comparison result of the number of nodes between them.This is to balance the size of the two trees.However,in difficult environments,this strategy can take a lot of time to expand a tree with few nodes and hindered growth.Besides,the new sampler and the bidirectional search are greedy,which leads to the problem where the algorithm may sample too many points in the local space.Therefore,a more flexible exchange method is needed to balance the search process of the two trees.

The exchange strategy of the new algorithm is consistent with the strategy of swapping according to the number of nodes under normal conditions,but when it fails,the new strategy will record the number of failures.If the recorded value is greater than thethreshold,the planner will enter the forced exchange process (Lines 6−13 in Algorithm 5).In the forced exchange process,R_Tand the number of nodes of each tree are used to calculate the current point density of the tree,and then the tree with lower point density is selected to carry out the sampling and expansion procedures described in Sections III-B and III-C to increase the number of nodes in the tree area.Finally,regardless of whether the expansion of the previous step is successful,two trees will be forced to swap.The new strategy can better balance the expansion of the two trees to increase the stability of the algorithm.

IV.ExPERIMENTS

In this section,we will compare the planning performance of RRT,RRT-Connect,RRV and the proposed ARRTConnect.The experiments include two types:A basic environmental test and integrated environmental test.Each type contains a variety of tests to compare the adaptability of each planner in different environments.All experiments are conducted on a machine with an Intel I7-7 700 3.6 GHz processor and 4 GB of memory.All algorithms have been written in Python and use an efficient multi-dimensional space search structure,R-tree [25],to quickly find the nearest neighbor.The expansion step of the tree is selected in {1,3}in the basic environmental test,and in {20,22} in the integrated environmental test.For local sampling after expansion failure in all tests,the sampling radius of RRV is 1.5 times the tree step size,while the two local expansion steps of ARRT-Connect are 1.5 times and 0.75 times the tree step size respectively.To speed up the planning,all algorithms are set to sample in the goal area with a probabilityPgoal=0.01 [26] and the parameterPousidein ARRT-Connect is set to 0.95 initially.The maximum number of sampling points is set to 25 000 for the basic environmental test and 20 000 for the integrated environmental test.If the path is not found within this limit,the planning is considered as a failure.Each experiment is tested 50 times to collect relevant data.The execution time,the total number of nodes in the tree and the success rate will be given for each result to evaluate the overall performance of the algorithms.To clearly show the time-consuming differences of different algorithms,all the time units are milliseconds.The execution time and the number of nodes are calculated using only data from successful planning in 50 tests,and the success rate represents the ratio of the number of successful path planning in 50 tests.

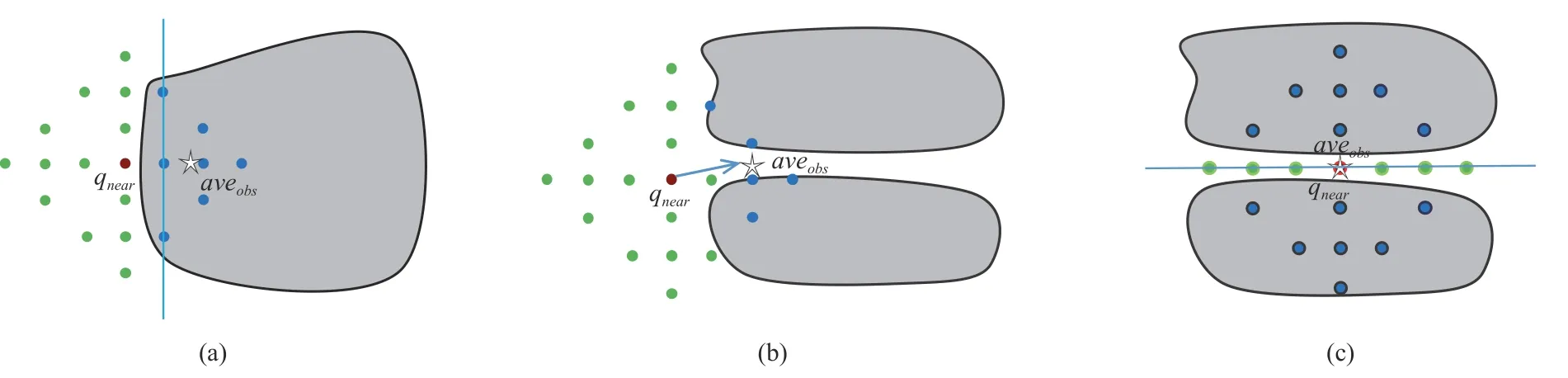
Fig.3.Three types of local environments.(a) Wall;(b) Entrance of the narrow passage;(c) Narrow passage.The red points are qnear and the star points are aveobs.The a veobs point in the obstacle area indicates that a wall-type obstacle is encountered.Otherwise,if a veobs and q near are far apart,q near is likely to be at the entrance of the narrow passage,and if they are close together,qnear may be in the narrow passage.Arrows or lines are the new extension directions for qnear.

A.Basic Environmental Test

In the basic environmental test,we will test different environments in two-dimensional and three-dimensional space.For two-dimensional tests,we test algorithms in four different environments and Fig.4 shows the planning results of four algorithms in these environments,where triangle and square points represent the starting and the target points respectively.The Simple environment is used to test the performance of the algorithms under easy obstacles.The purpose of the Cluttered environment is to test whether the performance of the new algorithm will not be significantly reduced due to additional calculations when dense obstacles are encountered.The planning paths in the Narrow and Bug Trap environments must pass through narrow passages.Therefore,in these two difficult environments,whether the algorithm can quickly find and pass through a narrow passage will be very important.From Figs.4 (a) and 4(b),we can find that the results of ARRT-Connect are similar to RRT-Connect and the tree nodes of these two algorithms are less than those of RRT and RRV.In Figs.4 (c) and 4(d),ARRT-Connect uses the fewest nodes to find the path,showing the best performance among the four algorithms.These results show that the new algorithm has strong planning ability and good adaptability in a normal environment and an environment with narrow passages.

The specific statistical results of the four algorithms in twodimensional environments are shown in Table I.From the column of average time in Table I,we can find that ARRTConnect gives the best results for Narrow and Bug Trap environments.In the test of the Narrow environment,the average planning time of RRT and RRT-Connect is 16 and 9 times that of ARRT-Connect respectively,while the planning time of RRV algorithm,which is good at handling with narrow passages,is 4 times that of the new algorithm.For the Bug Trap environment,the planning time of RRT and RRTConnect is about 57 times that of ARRT-Connect,and the time consumption of RRV is about 28 times that of ARRTConnect.Moreover,neither RRT nor RRT-Connect is able to plan a path in all tests in these two environments,while both RRV and ARRT-Connect have a 100% success rate.For the other two environments that do not contain narrow passages,RRT-Connect takes the least time,and the new algorithm follows closely behind.Although the time consumption of ARRT-Connect in these two environments is not the lowest,its performance is 2–5 times faster than RRT and 6–10 times faster than RRV,so it can efficiently complete planning tasks in the multi-obstacle environment.

In terms of the variance of time consumption,ARRTConnect performs well,especially in difficult environments,which reflects the stability of the new algorithm in various environments.It can also be seen from Table I that the new algorithm has the lowest average number of sampling points in all tests,that is,the new algorithm can use fewer points to explore the space and provide feasible planning results,which reflects the efficiency of ARRT-Connect from another aspect.

To test the influence of the sampler and the exchange strategy on the planning results,we changed the sampler and exchange strategy respectively and carried out the test in the above two-dimensional environments.Table II shows the effect of the new sampler on the performance of the ARRTConnect algorithm.In Table II,the Free sampler means that only the sampling points in the free area are accepted,while the Greedy sampler is the new sampler described in Section III-B.The results show that ARRT-Connect with Greedy sampler performs best in all tests,where not only the average planning time of the algorithm is lower,but also the standard deviation is smaller and the performance is more stable.In the test of the Simple environment,the results of the two samplers are similar.This is because the Simple environment is easy and only a few sampling points are needed to complete the planning,so they are all less time-consuming.

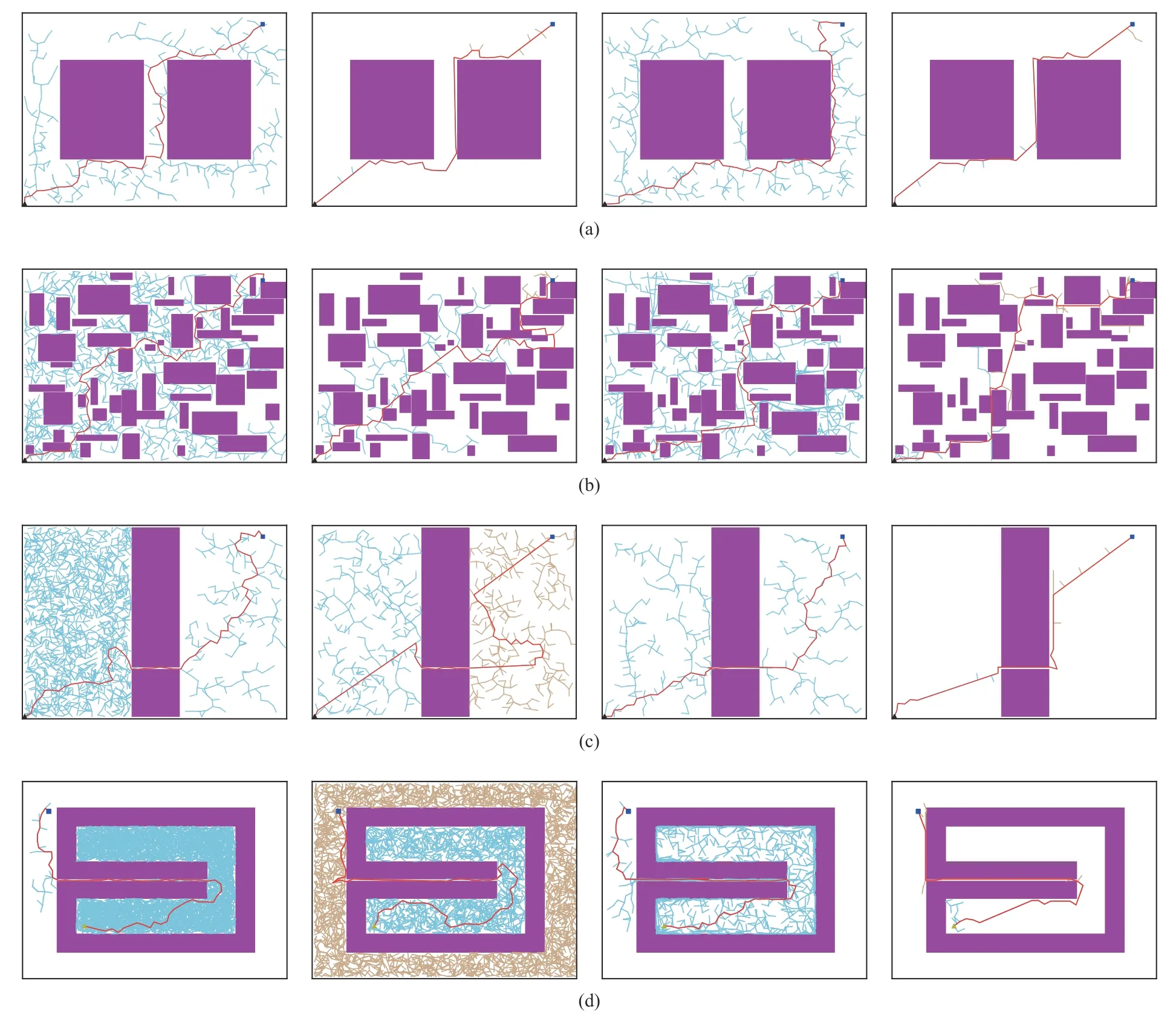
Fig.4.Planning results of four algorithms for two-dimensional environments,in which the triangle points are the starting points and the square points are the target points.From left to right in each row are the planning results of RRT,RRT-Connect,RRV and ARRT-Connect algorithms.(a) Simple;(b) Cluttered;(c)Narrow;(d) Bug Trap.

Table III compares the performance of ARRT-Connect with three different exchange strategies,namely swapping at each iteration,swapping according to the number of nodes of the two trees,and the proposed adaptive swapping.Similar to Table II,the new swap strategy performs best on most tests,and the variance of the algorithm’s time consumption with the newly proposed exchange strategy is always the lowest.It indicates that the proposed exchange strategy can better solve the problem of search direction replacement,thus reducing the time consumption of the algorithm when one direction can not be expanded.

For three-dimensional tests,the algorithms are tested in three different environments (Fig.5),among which the Simple3d and Narrow3d environments are the threedimensional extensions of the corresponding environments in two-dimensional space respectively,while the Multi-Narrow3d is a more difficult environment similar to the Narrow3d.Moreover,in Narrow3d and Multi-Narrow3d environments,the feasible path must pass through narrow passages.The statistical results are given in Table IV.Results on the Simple3d environment show that bidirectional search is far more efficient than one-way search,with average time consumption only about one-tenth of that of one-way search.Meanwhile,the performance of ARRT-Connect and RRTConnect is basically the same.In the other two tests,ARRTConnect is the algorithm with the best performance.The average planning time of RRT-Connect is 2–5 times that of ARRT-Connect,and the performance of the other two algorithms are worse.Furthermore,ARRT-Connect has the least number of sampling points in all tests,and the variance is small,showing the same stability as the two-dimensional space tests.Fig.6 shows clearly that the ARRT-Connect can complete the planning task with fewer points in the Narrow3d environment,which intuitively reflects the efficiency of the proposed algorithm.

B.Integrated Environmental Test

In this experiment,we will test the algorithms on a simulated office map.It is more convenient to place different obstacles by using the simulated office map.The size of the map is 2 413 × 1 268 and there are four rooms A,B,C and D on the office map (Fig.7).Room A is a grocery store with alot of obstacles.Rooms B and C are similar to meeting rooms or waiting rooms,so there are only a few simple obstacles,while room D is equivalent to a room with large equipment and contains simple narrow passages.Four scenarios will be tested in the experiment.The first three scenarios are the planning from room A,B,C to room D,that is,the path planning from the ordinary obstacle environments to a narrow passage environment.The fourth scenario is the planning from room B to room C to test the performance of the algorithm in a normal environment.The statistics are given in Table V.The path results of Scenario I to IV are shown in Fig.8.Table V shows that the proposed algorithm performs best in all tests.Furthermore,in the first three scenarios,RRT takes the longest time and has the lowest success rate,which shows that RRT can not deal with the planning problem of an environment with narrow passages well.Because the narrow passages in the map are relatively simple,RRT-Connect can complete all the planning,and the time consumption is lower than the RRV algorithm.This indicates the high efficiency of dual-tree search,and also reflects the problem where even though RRV can cope with narrow passages,its efficiency will be reduced when encountering common obstacles.ARRT-Connect has obvious advantages in these three scenarios.Besides low time consumption,the variance of time consumption is also small,which shows the stability of the proposed algorithm.For the fourth scenario,the performance of ARRT-Connect and RRT-Connect is basically the same,and both of them are better than the other two algorithms.This once again proves the adaptability of the new algorithm,that is,the planning performance of the new algorithm under a normal environment is not significantly affected by the additional computation added to cope with narrow passages.

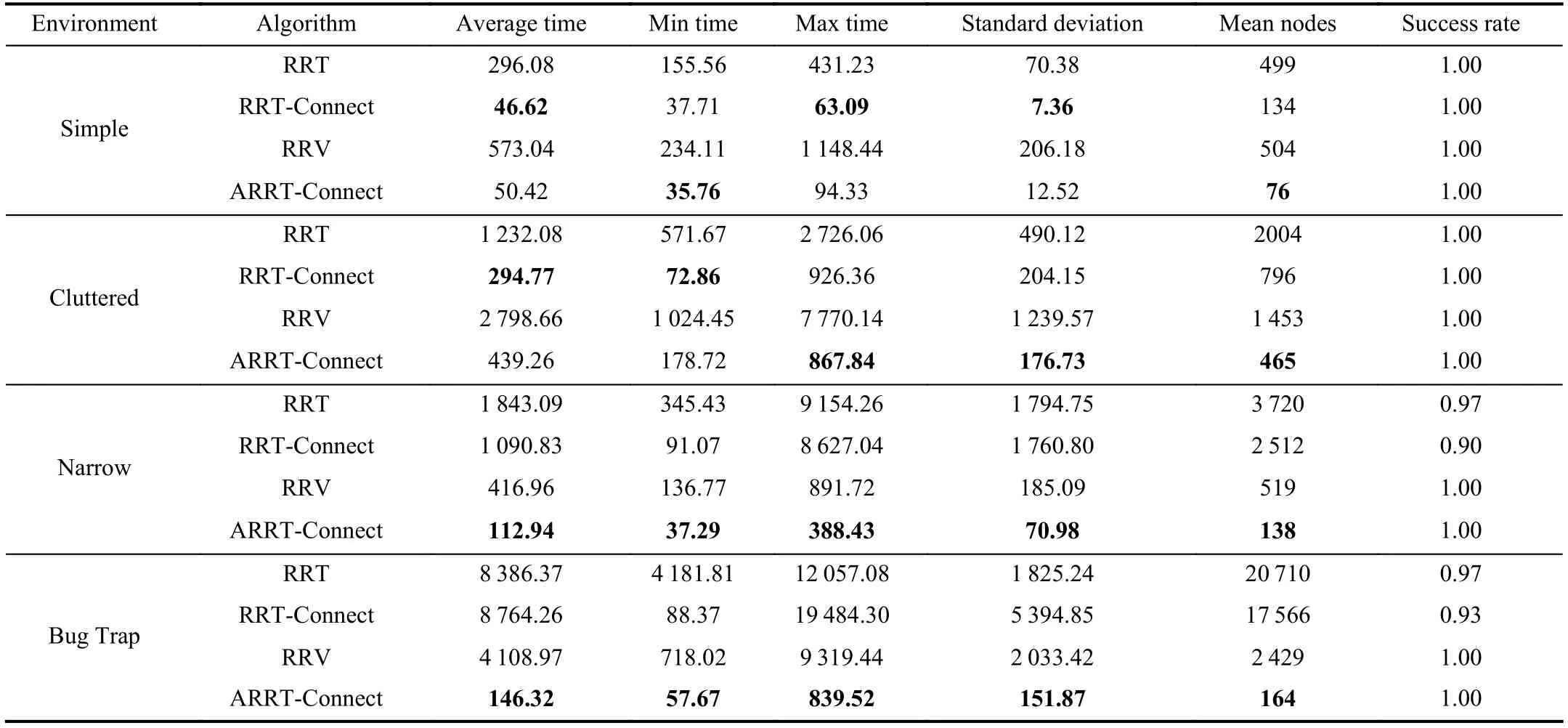
TABLE IRESULTS FOR PLANNNING IN DIFFERENT TWO-DIMENSIONAL ENVIRONMENTS

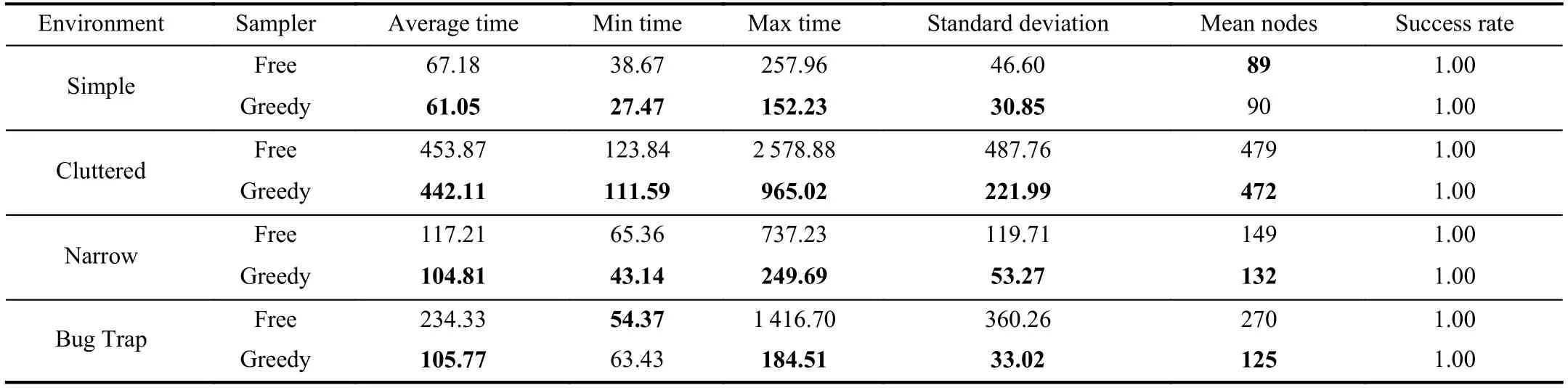
TABLE IIRESULTS FOR NEW ALGORITHM WITH DIFFERENT SAMPLERS

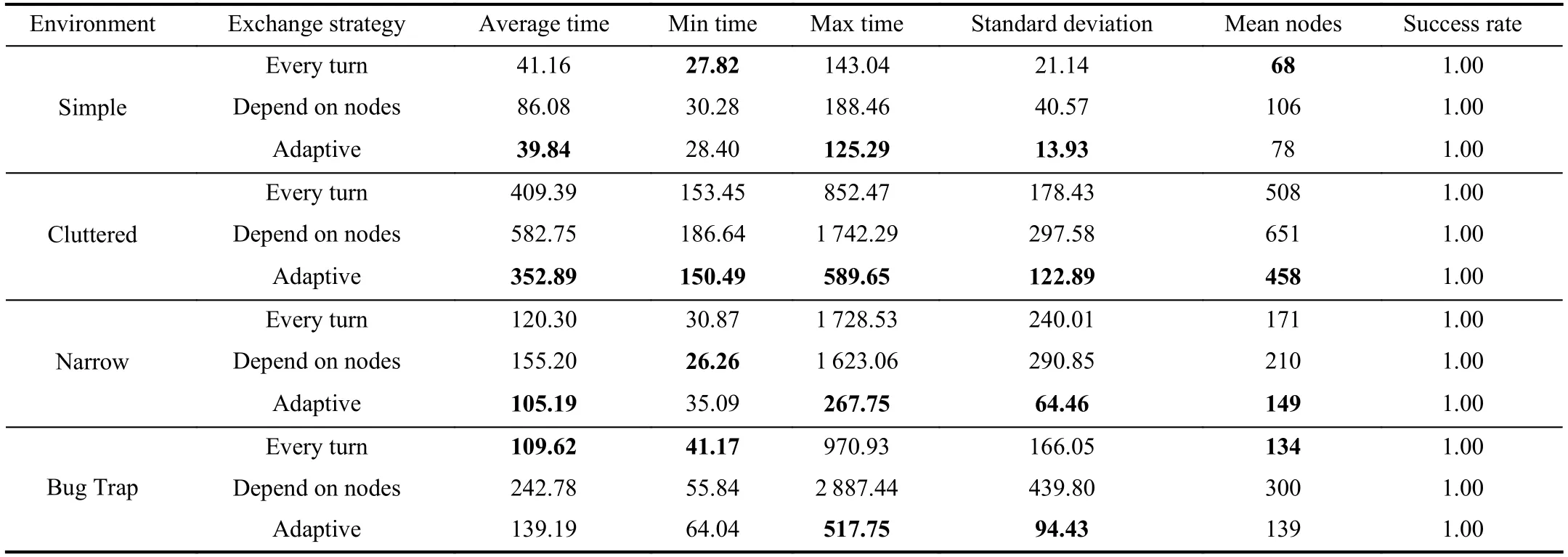
TABLE IIIRESULTS FOR NEW ALGORITHM WITH DIFFERENT ExCHANGE STRATEGIES

Fig.5.Experimental environments in three-dimensional space,in which the triangle points are the starting points and the square points are the target points.(a) Simple3d;(b) Narrow3d;(c) Multi-Narrow3d.

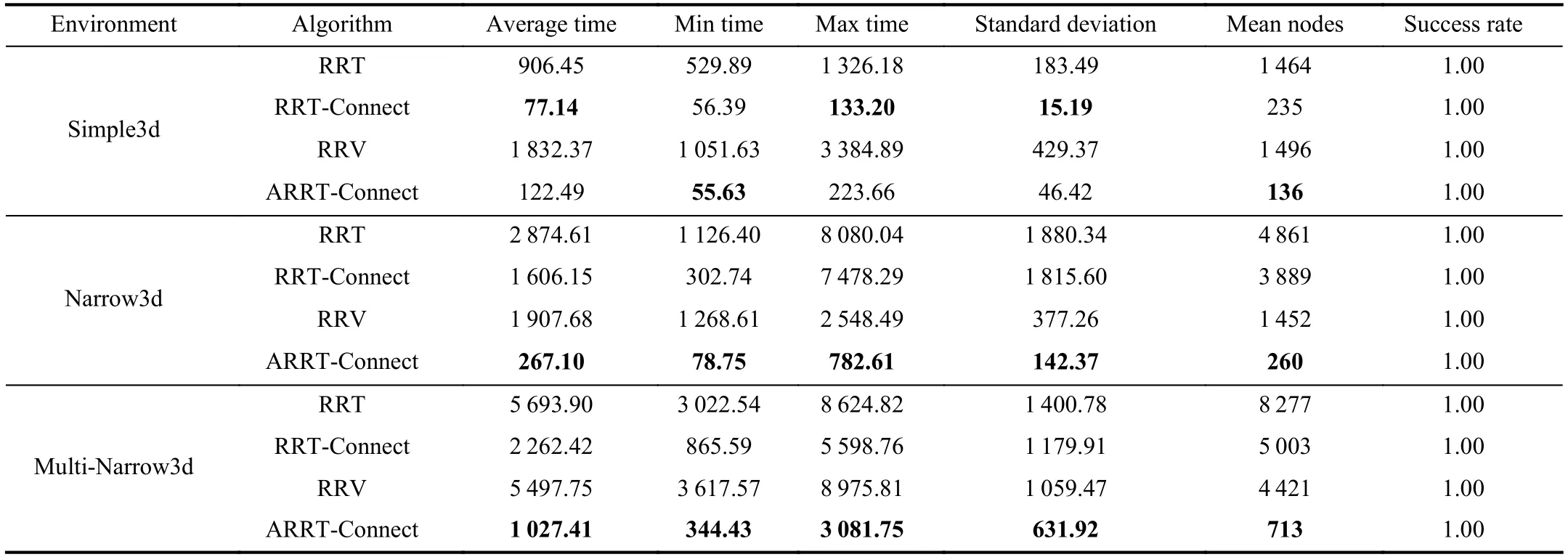
TABLE IVRESULTS FOR PLANNING IN DIFFERENT THREE-DIMENSIONAL ENVIRONMENTS

V.DISCUSSIONS

There are two important parts in ARRT-Connect,one is the sampling probability of the new sampler in the area outside the tree at the beginning,and the other is the sampling range during local sampling.The sampling probability outside the tree influences the overall behavior of the sampler,thereby influencing the way the tree explores the space.In ARRTConnect,this probability is determined byPoutside.If the initial value ofPoutsideis small,the search tree will tend to sample within the tree,and the expansion speed of the tree will slow down.Gradually,the point density within the tree will increase,which can better describe the spatial structure within the tree.IfPoutsideis large,the search tree will tend to expand outwards,so that the tree can explore more space with fewer points,thereby increasing search efficiency.ARRTConnect initially sets the value ofPoutsideto be large,and gradually decreases the value ofPoutsideas the number of sampling points increases,so that the algorithm can better explore the space.The range of local sampling affects the quality of the local information obtained.If the sampling range is too large,the sampling points can not describe the local spatial information near the nearest neighbor point.On the contrary,the sampling points will not give the structure of local space accurately,so a moderate local sampling range can better guide the expansion of the tree.

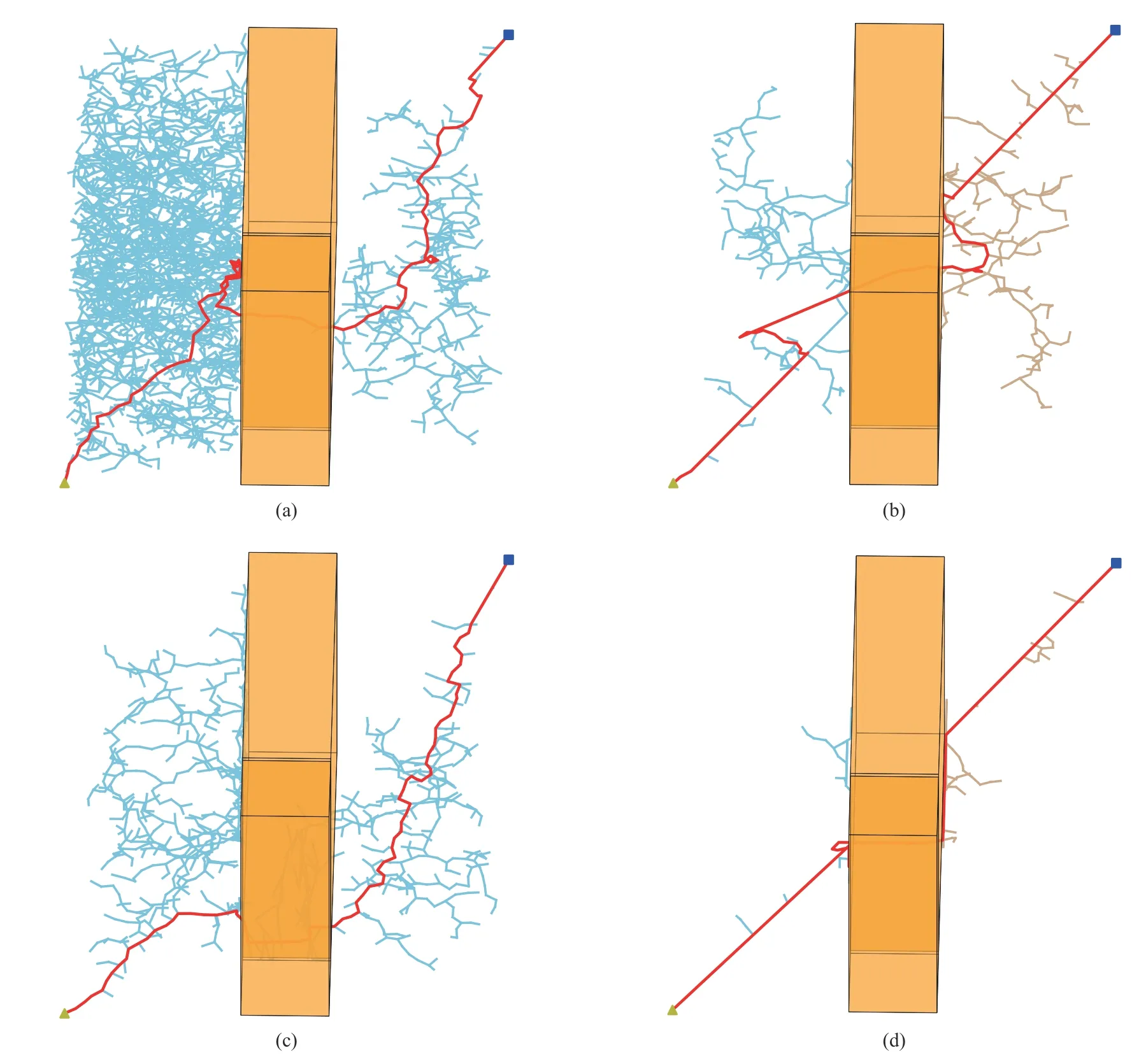
Fig.6.Planning results of four algorithms for Narrow3d environment.(a) RRT;(b) RRT-Connect;(c) RRV;(d) ARRT-Connect.

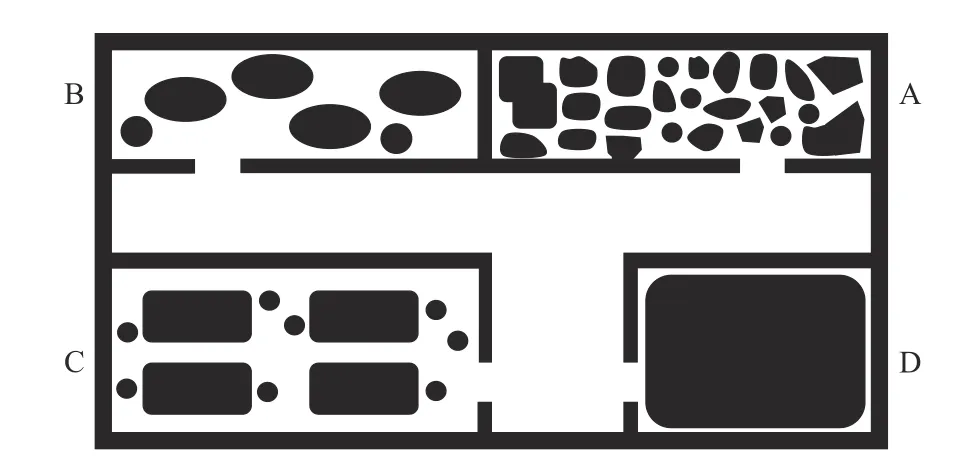
Fig.7.Office map used in the integrated environmental test.There are four rooms A,B,C and D in anticlockwise order from the upper right corner.

In addition to the aforementioned key points,there is a small defect in the environmental judgment process,that is,the concave obstacles may be judged as the narrow passages or the entrance of the narrow passages,which will increase the time consumption of the algorithm.However,because the proposed algorithm uses bidirectional search and improves the exchange strategy,the planner will try to expand in the other direction when the tree falls into a situation where it cannot be expanded in one direction,thereby reducing the impact of incorrect judgments.

VI.CONCLUSIONS

In this paper,a new algorithm based on RRT-Connect and RRV is proposed to deal with the motion planning problems with narrow passages.The proposed algorithm (ARRTConnect) combines a new greedy sampler,an environmental judgment process,and a flexible two-way exchange strategy to achieve the best results compared with RRT,RRT-Connect and RRV in an environment with narrow passages.Among them,the environmental judgment process can use information obtained from local sampling to calculate a new feasible direction (e.g.,along the surface of an obstacle or along a narrow passage) for the nearest neighbor point that fails to expand.Due to the extra calculation time required in the judgment process,the performance of ARRT-Connect in a cluttered environment has weakened.Bidirectional search and the proposed sampler reduce this influence and accelerate the planning speed.Therefore,the performance of the new algorithm in a cluttered environment is closer to RRTConnect,and the new algorithm can adapt to various environments.We also discuss the key factors that have an impact on the efficiency of the algorithm,and their influence on the behavior of ARRT-Connect is analyzed.This gives the direction for further research on this kind of algorithm.

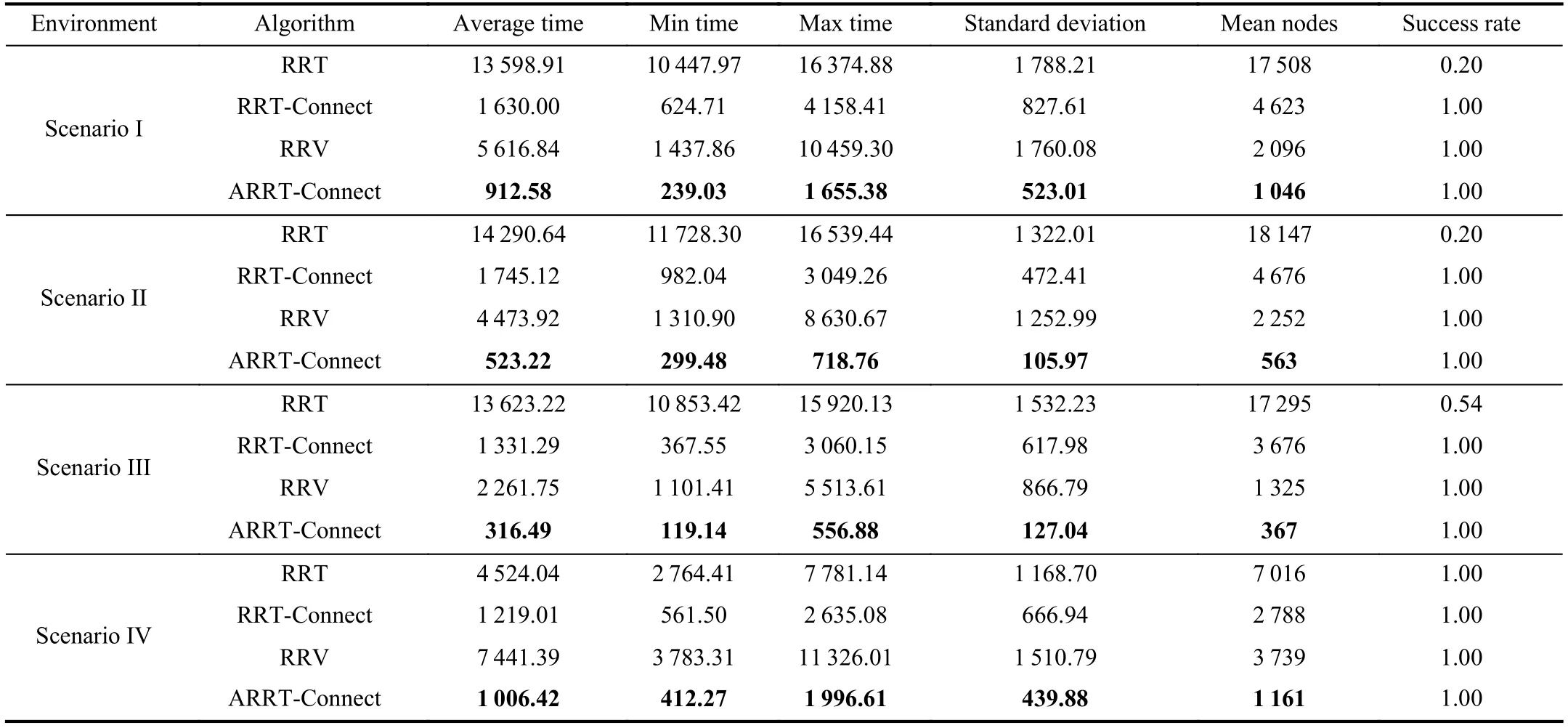
TABLE VRESULTS FOR PLANNING IN INTEGRATED ENVIRONMENT

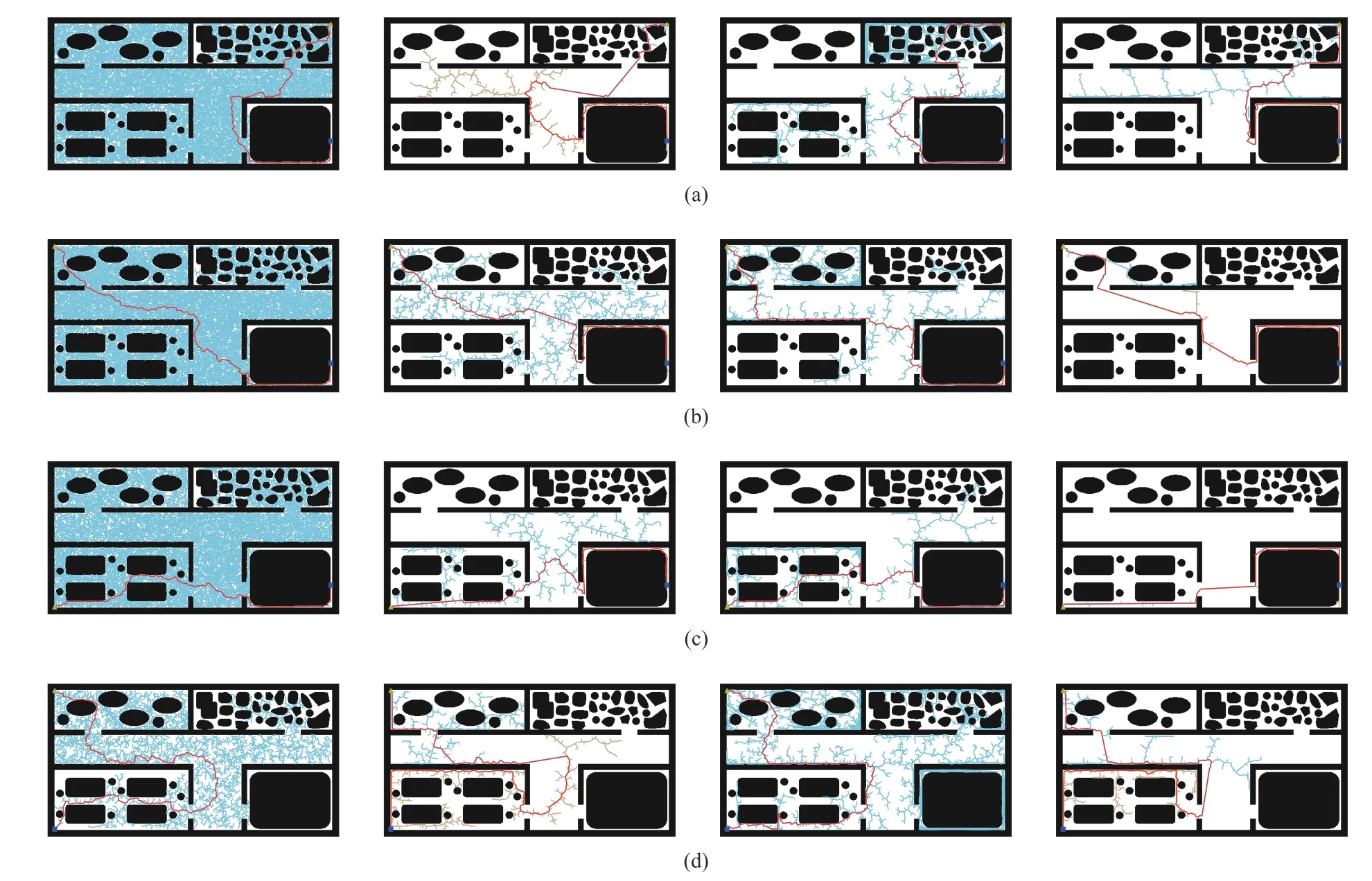
Fig.8.Planning results of four algorithms for office map.From left to right in each row are the planning results of RRT,RRT-Connect,RRV and ARRTConnect algorithms.(a) Room A to D;(b) Room B to D;(c) Room C to D;(d) Room B to C.