Computation of Minimal Siphons in Petri Nets Using Problem Partitioning Approaches
2022-01-25DanYouOussamaKarouiAssociateandShouguangWangSenior
Dan You,,Oussama Karoui, Associate,and Shouguang Wang, Senior
Abstract—A large amount of research has shown the vitality of siphon enumeration in the analysis and control of deadlocks in various resource-allocation systems modeled by Petri nets (PNs).In this paper,we propose an algorithm for the enumeration of minimal siphons in PN based on problem decomposition.The proposed algorithm is an improved version of the global partitioning minimal-siphon enumeration (GPMSE) proposed by Cordone et al.(2005) in IEEE Transactions on Systems,Man,and Cybernetics—Part A:Systems and Humans,which is widely used in the literature to compute minimal siphons.The experimental results show that the proposed algorithm consumes lower computational time and memory compared with GPMSE,which becomes more evident when the size of the handled net grows.
I.INTRODUCTION
PETRI nets (PNs) [1]–[4] are a well-recognized mathematical tool suitable for the modeling,analysis,and control of resource-allocation systems [5],[6].The analysis of PNs may be performed in different ways such as structural analysis and reachability analysis.A lot of effort has been devoted to structural analysis due to its advantage of low computational cost.Siphons [7],which are particular sets of places in a PN,are often utilized to detect the liveness of a considered net.More specifically,the liveness of a PN is closely related to whether siphons are sufficiently marked[8]–[14].For ordinary PNs,the occurrence of deadlocks is due to the emptiness of some siphon,which leads to some transitions disabled permanently [15]–[17].
A seminal work to prevent deadlocks in automated manufacturing systems was established by Ezpeletaet al.[18]for a class of ordinary PNs called systems of simple sequential processes with resources (S3PR).In more detail,they add a monitor (i.e.,a control place) for each unmarked strict minimal siphon such that all output arcs of the monitor are linked with source transitions of the net.When all siphons are controlled,the augmented net is live.Note that,in this method,complete siphon enumeration is required since a monitor is added for each siphon in the net.As we know,the number of siphons grows exponentially with respect to the net size [19],[20],the method thus suffers from high computational complexity.Indeed,deadlock resolution policies based on siphon control all require the complete or partial siphon enumeration [21],[22].To improve the computational efficiency of such methods,it is of great importance to improve the efficiency of siphon computation.
A.Literature Review
There are a variety of methods in the literature that compute siphons.These methods can be classified into two categories in terms of application scope.One applies to special classes of PNs.For instance,methods based on parallel algorithms [23],resource circuits [24],[25],pruning-graphs [26],genetic algorithms [27],[28] and loop resource subsets [12].The other applies to arbitrary classes of PNs such as linear integer programming methods [16],[29],integrated net analyzer(INA)-based methods [30],methods based on semi-tensor product of matrices [31] and problem decomposition [32].Methods in the first category are basically much more efficient in computation than those in the second category,whereas methods in the second category have the advantage of having no restriction on the class of PN.
This work focuses on siphon computation methods that are applicable to arbitrary classes of PNs.To our best knowledge,among all the methods in the literature applicable to arbitrary classes of PNs,the methods proposed by Cordoneet al.[32]are the most efficient ones.Their methods are based on the idea of problem decomposition.To put it simply,the idea is that a problem is decomposed into multiple sub-problems so that the solution of the original problem can be deduced by combining the solutions of all the sub-problems.Cordoneet al.[32] developed two siphon enumeration approaches based on the technique of problem decomposition,namely,global partitioning minimal-siphon enumeration (GPMSE)and local partitioning minimal-siphon enumeration (LPMSE).They have been used extensively in the literature due to their low computational complexity.The main difference between them is that GPMSE allows a current problem to be decomposed using a siphon that is already found before,whereas LPMSE requires getting a solution (i.e.,a siphon) to the current problem first and then using the siphon to decompose the current problem.Although GPMSE and LPMSE have good performance,they still have some drawbacks.In more detail,GPMSE can hardly be applied to nets with large size,whereas LPMSE might generate nonminimal siphons.
B.Contributions of This Work
In this study,we propose an improved version of GPMSE that we name improved GPMSE (IGPMSE).IGPMSE enumerates minimal siphons in a PN with less consumption on CPU time and memory space than the original version so that it is readily applicable to large-size nets.Such improvements are realized mainly based on the following ideas:
1) We expand as large as possible a set of places that are forced to be contained in a minimal siphon to be found;
2) We deduce more conditions under which there is no need to further partition a problem,i.e.,more conditions to terminate the partition of a problem;and
3) We adopt a depth-first search for the enumeration of minimal siphons rather than the width-first search performed in [32].
We notice that the first two ideas aim to reduce the number of sub-problems generated during the procedure of siphon enumeration,while the third idea aims to reduce memory consumption.Indeed,it is validated by experimental results that IGPMSE behaves better than GPMSE in both computational time and memory consumption.
C.Organization of This Paper
The rest of this paper is organized as follows.Section II recalls basic notions of PNs.Section III introduces siphons and their related properties which are involved in the paper.In Section IV,we first present some preliminary functions and results,then introduce the algorithm of IGPMSE,and finally provide an illustrative example.Section V presents the comparison between IGPMSE and GPMSE.We conclude this paper in Section VI along with our further research work.
II.PRELIMINARIES OF PETRI NETS
In this section,we recall the basics of Petri nets [33] and siphons.
A Petri net (PN) Σ is a three-tuple (P,T,F),where
-Pis the set of places;
-Tis the set of transitions;and
-F⊆ (P×T)∪(T×P) represents directed arcs of the net.
The preset and post-set of a nodez∈P∪Tare denoted by•zandz•,defined as
•z={z'∈P∪T|(z',z) ∈F} andz•={z'∈P∪T|(z,z') ∈F},respectively.Moreover,it is defined that••z=•(•z) andz••=(z•)•.Furthermore,given a set of nodesZ⊆P∪T,it is defined that•Z=∪z∈Z•z,andZ•=∪z∈Zz•.
A transitiont∈Tis said to be a sink transition ift•=∅ and a source transition if•t=∅.Similarly,a placep∈Pis said to be a sink place ifp•=∅ or a source place if•p=∅.
Given a PN Σ=(P,T,F),a subset of placesP'⊆Pand a subset of transitionsT'⊆T,the subnet of Σ generated byP'andT'is Σ'=(P',T',F'),whereF'=[(P'×T') ∪ (T'×P')]∩F.
III.SIPHONS AND THEIR PROPERTIES
A non-empty setS⊆Pis called a siphon if•S⊆S•.A siphon is said to be minimal if it does not contain any other siphon.
In the following,we report two properties related to siphons that are the known results in the literature.
Property 1 [32]:Let Σ=(P,T,F) be a PN and {p}⊆Psuch that•p=∅.Then,{p} is a minimal siphon.
Property 1 indicates that every source place constitutes a set that is a minimal siphon.
Property 2 [32]:Let Σ=(P,T,F) be a PN.The setPis a siphon if•t≠ ∅,∀t∈T.
By Property 2,the set of all places in a PN is a siphon if the net contains no source transition.
IV.COMPUTATION OF MINIMAL SIPHONS IN PN
In this section,we propose a method of minimal-siphon computation in a PN based on problem decomposition,namely,improved GPMSE (IGPMSE).To this end,we first formally define aproblemthat is discussed throughout the paper.
Definition 1:Let Σ=(P,T,F) be a PN andPΩ⊆P.We define Δ=(Σ,PΩ) aproblemthat finds the set of all minimal siphons containingPΩin the net Σ.We use ΠΔto denote the set of all solutions to the problem Δ=(Σ,PΩ),i.e.,ΠΔdenotes the set of all minimal siphons containingPΩin the net Σ.
We notice that,in the case thatPΩ=∅,Δ=(Σ,PΩ) is a problem that finds the set of all minimal siphons in the net Σ,which is exactly what we aim to solve in this paper.We will see later how this problem is solved by decomposing itself into several sub-problems whose solutions together constitute the solution space of the original problem.
In the remainder of this section,we first provide several functions that will be called in our proposed method,i.e.,IGPMSE,and prove some results related to these functions,and then we introduce IGPMSE in detail.
A.Preliminary Functions and Results
We first introduce a function namedHandleSourcePlace.We can see that this function returns a set that stores every set consisting of a single source place in the given net and it obtains a reduced net by eliminating all source places from the net.We have the following result regarding the function.It indicates that the set of minimal siphons in the original net consists of minimal siphons in the reduced net and all sets consisting of a source place.


Result 1:Given a PN Σ=(P,T,F) and (Σ',Θ)=HandleSourcePlace(Σ),it holds that ΠΔ1=ΠΔ2∪Θ,where Δ1=(Σ,∅) and Δ2=(Σ′,∅).
Proof:It is clear that Θ={{p}|•p=∅}.By Property 1,ΠΔ1⊇Θ holds.We can see that FunctionHandleSourcePlacesremoves all the source places from Σ but preserves all the transitions connected to places.Thus,any minimal siphonS'in Σ' is a minimal siphon in Σ and any minimal siphonSin Σ is either a set consisting of a single source place,i.e.,S∈ Θ or a minimal siphon in Σ'.Thus,the result follows.
The following function namedReduceNetSizecan be used to simplify the net that we consider.In simple words,it first repeatedly deletes source transitions and their output places in the considered net and then repeatedly deletes sink places/transitions.Result 2 indicates that such a simplification procedure performed byReduceNetSizehas no impact on the minimal-siphon enumeration result.

Result 2:Given two PNs Σ and Σ',a set of placesPΩ,and two problems Δ1=(Σ,PΩ) and Δ2=(Σ′,PΩ),it holds that ΠΔ1=ΠΔ2if Σ'=ReduceNetSize(Σ).
Proof:Places connected to source transitions cannot belong to any siphon because no other places can have these transitions in their postset.Thus,we may repeatedly delete source transitions and their output places and the minimalsiphon enumeration results are the same in the original net and the reduced net.Now,we consider sink transitions.It is trivial to see that whether sink transitions exist will not change the siphon enumeration result.Thus,they can be removed.Finally,we consider sink places.Letpbe a sink place.Sincep•=∅ and•p≠ ∅,{p} cannot be a siphon.Moreover,letSbe a siphon including the sink placep.It holds that•(S{p}) ⊆•Sand (S{p})•=S•.SinceSis a siphon,it is•S⊆S•.It thus follows that•(S{p}) ⊆ (S{p})•.It means thatSis not a minimal siphon.In other words,any siphon including a sink place cannot be minimal.Thus,we may delete sink places whose removal will not change the minimal-siphon enumeration result.Consequently,the result follows.
We infer that functionsHandleSourcePlaceandReduceNetSizecan reduce significantly the size of a net and therefore facilitate the enumeration process of minimal siphons.
The next function,namedExpand,is used to expand the setPΩof places that must be included in a minimal siphon.In other words,due to some properties of minimal siphons,we may know that,in the case that some places are required to be included in a minimal siphon,some other places are definitely included.Specifically,as performed inExpand,when the setPΩis given,there are two cases to expandPΩ:1) If there exists an input but not output transition of the setPΩsuch that it has only one input placep',the placep'can be included to expandPΩ;and 2) If there exists a placepinPΩand another placep' out ofPΩsuch thatp' is the unique output place ofp,the placep'can be included to expandPΩ.Result 3 indicates that such an expanding procedure onPΩdoes not change the minimal-siphon enumeration result.It is worth noting that,typically,the bigger the setPΩis,the faster a solution to the corresponding problem may be derived.Thus,the functionExpandmay be used later to fasten the process of searching minimal siphons.

Result 3:Given a PN Σ without source places,two sets of placesPΩandPΩ',and two problems Δ1=(Σ,PΩ) and Δ2=(Σ,PΩ′),it holds that ΠΔ1=ΠΔ2ifPΩ'=Expand(PΩ,Σ).
Proof:SincePΩ' ⊇PΩ,a minimal siphon containingPΩ' is definitely a minimal siphon containingPΩ,i.e.,ΠΔ1⊇ΠΔ2holds.Next,we prove a minimal siphon containingPΩis also a minimal siphon containingPΩ',i.e.,ΠΔ1⊆ΠΔ2.Consider thatt∈•PΩPΩ•such that•t={p'}.LetSbe a minimal siphon containingPΩ.We can see thatp' ∈Ssince otherwiset∈•Sbutt∉S•,which contradicts the fact thatSis a siphon.Thus,the setPΩcan be iteratively expanded by including the placep'.Now,consider thatp∈PΩ,andp' ∈PPΩsuch thatp••={p'}.LetSbe a minimal siphon containingPΩ.We prove thatp' ∈S.By contradiction,suppose thatp' ∉S.LetT'=•p'∧p•.It holds thatT'⊄•SandT'⊂S•.LetPX=•T'∩S.We have(SPX)•=S•T'.Moreover,it is clear that•(SPX) ⊆•S.SinceT'⊄•S,it follows that•(SPX) ⊆•ST'.Consequently,we have•(SPX) ⊆ (SPX)•.It means thatSPXis a siphon,which contradicts the fact thatSis a minimal siphon.Therefore,it holds thatp' ∈S.Thus,the setPΩcan be iteratively expanded by including the placep'.By the above analysis,ΠΔ1⊆ΠΔ2holds.Consequently,the result follows.
In what follows,we present functionPomegaMiniSiphonthat was exhibited in the work of Cordoneet al.[32].Given a PN without source transitions and a setPΩof places,PomegaMiniSiphonreturns aPΩ-minimal siphon in the net.We notice that the notion of aPΩ-minimal siphon is not the same as the notion of a minimal siphon containingPΩ.The formal definition of aPΩ-minimal siphon is as follows:
Given a siphonSand a set of placesPΩ⊆P,Sis calledPΩminimal ifScontains all the places inPΩandSdoes not contain any other siphon that contains all the places inPΩ.
We can see that aPΩ-minimal siphon is not necessarily a minimal siphon except the case thatPΩ=∅.

The computation ofPomegaMiniSiphonis detailed as follows.If the givenPΩis the whole set of places of the considered net,PΩitself is aPΩ-minimal siphon;and otherwise,we find aPΩ-minimal siphon by the following operations:
We delete each placep∈PPΩfrom the considered net and then repeatedly delete resultant source transitions and their output places.If any place inPΩis deleted due to the above operations,we restore the net to its original structure before deletingp,expandPΩby includingp,and then go to the next iteration to delete the next place inPPΩ;and otherwise,we directly go to the next iteration to delete the next place inPPΩ.We repeat the above operations untilPΩis the whole set of places of the resultant net andPΩnow is a solution.
Result 4:Given a PN Σ=(P,T,F) without source transitions and a set of placesPΩ⊆P,S=PomegaMiniSiphon(Σ,PΩ) is aPΩ-minimal siphon.
Proof:By FunctionPomegaMiniSiphon,we can see that the subnet of Σ generated bySand•S∪S•contains no source transition.Thus,Sis a siphon due to Property 2.
By contradiction,suppose thatSis not aPΩ-minimal siphon.LetS'⊂Sbe a siphon containingPΩandp∈SS'.Sincep∈S,according to FunctionPomegaMiniSiphon,there is a path frompto a placep'∈PΩsuch that every transition in the path has only one input place.Sincep'∈PΩ,it is clear thatp'∈S'.It thus follows thatp∈S'since otherwiseS'cannot be a siphon.This,however,contradicts the fact thatp∉S'.Consequently,we may conclude thatSis aPΩ-minimal siphon.
We finally present a functionSiphonIsMini,which checks if a given siphon containing two or more places is minimal.Specifically,we first obtain the subnet Σsgenerated bySand•S∩S•and then for each place inS,the following procedure is performed:we delete the place and its related arcs from the considered net and thenReduceNetSizeis called to handle the resultant net.In the case thatReduceNetSizereturns a nonempty net,we may conclude that the siphonSis not minimal.i.e.,ans=Flase;otherwise,after checking all the places inS,we may conclude that the siphonSis minimal.i.e.,ans=True.

Result 5:Given a siphonSwith |S| ≥ 2,Sis minimaliff SiphonIsMini(S)=True.
Proof:(=>) By contradiction,suppose thatSis not minimal.In other words,there is a siphonS'⊂S.Letp∈SS'.Let Σ'=DeletePlace(Σs,p) and Σ''=ReduceNetSize(Σ').We can see thatS'is a siphon in Σ'.SinceSiphonIsMini(S)=True,it is Σ''=∅.By Result 2,there is no minimal siphon in Σ' since there is no minimal siphon in Σ''.Thus,there is no siphon in Σ',which,however,contradicts thatS'is a siphon in Σ'.As a result,Sis minimal.
(<=) By contradiction,suppose thatSiphonIsMini(S)=False.It indicates that ∃p∈Ssuch thatReduceNetSize(Σ') ≠∅,where Σ'=DeletePlace(Σs,p).Let Σ''=(P'',T'',F'')=ReduceNetSize(Σ').We can see that there is no source transition in Σ''.By Property 2,P''is a siphon.SinceP''⊆S,the siphonSis not minimal,which contradicts the fact thatSis minimal.As a result,it isSiphonIsMini(S)=True.
B.Minimal Siphon Computation Using IGPMSE


In this section,we propose an improved algorithm of GPMSE,named IGPMSE.The improvements mainly lie in:1) We expand the set of places required to be included in a minimal siphon to be found;2) We add a condition that terminates the further decomposition on a problem,i.e.,PΩis a siphon;and 3) The depth-first search is adopted in IGPMSE whereas GPMSE uses the width-first search.The first two improvements may result in a significant decrease in the number of sub-problems to be solved and the third improvement may save the memory consumption.
We explain Algorithm 1 (IGPMSE) as follows.The set Θ is used to save all the found minimal siphons.
First,functionsHandleSourcePlaceandReduceNetSizeare called to find all minimal siphons that consist of a single source place and remove places and transitions that are not needed for the further search of minimal siphons.Next,we create the root node (Σ,∅) of a tree and use functionPomegaMiniSiphonto find a minimal siphon.Note that,we establish a linked list Γ to store minimal siphons that are used for decomposing problems.By callingCreateNewNode(Σ,∅,index,Θ),we decompose the problem (Σ,∅) using the minimal siphon stored in Γ[index].In the following,we explain the functionCreateNewNode(Σ,PΩ,index,Θ) in detail.
CreateNewNode(Σ,PΩ,index,Θ) is a recursive function.It iteratively decomposes problems using the depth-first search.The variableindexindicates that we use the minimal siphon in Γ[index] to decompose the problem (Σ,PΩ).Note that,as shown in Steps 1–7,if Γ[index] is empty,we need to compute a minimal siphon and store it in Γ[index].Now,we start the decomposition of the problem (Σ,PΩ) using the minimal siphonSin Γ[index].We delete places inSPΩone after another to generate sub-problems.In order to get a subproblem easy to be solved,after deleting a placepfrom the net Σ,we further reduce its net size and expand the setPΩto a new setPΩ'',by calling functionsReduceNetSizeandExpand,respectively.In the case that the resultant net Σ' is not empty,we create a new node (Σ',PΩ'') in the tree.Regarding the new node,there are two cases to terminate the further decomposition on it:1)PΩ''⊄P';and 2)PΩ'' is a siphon.In any other cases,we continue the decomposition of the problem (Σ',PΩ'') by callingCreateNewNode(Σ',PΩ'',index+1,Θ).Note that,in the case that we terminate the decomposition on (Σ',PΩ''),ifPΩ'' is a siphon,we determine if it is minimal.If so,we should includePΩ'' in the set Θ.Besides,when we consider generating the next sub-problem of (Σ,PΩ) by deleting another place inSPΩ,the currently deleted placepshould be included in the setPΩconsidered in that sub-problem (see Step 26).By repeating the above procedure,we finish the construction of the tree when no node needs to be further decomposed and the final set Θ is the set of all minimal siphons in the handled PN.
We finally notice that problems in the same level of the tree are decomposed using the same minimal siphon.In particular,we use the minimal siphon in Γ[i] to decompose all the problems in leveli.
In what follows,we prove Algorithm 1 (IGPMSE)computes the set of all minimal siphons in a PN.To this end,we need the following two lemmas.
Lemma 1:Let Σ=(P,T,F) be a PN,PΩ⊆Pbe a set of places,Δ=(Σ,PΩ) be the problem of finding the set ΠΔof all minimal siphons containingPΩof Σ andS={p1,p2,…,pn}be a set of places.We have

Proof:The problem of finding the set ΠΔof all minimal siphons containingPΩof Σ can be decomposed inton+1 subproblems,that is
1) Finding the set of all minimal siphons of Σ excludingp1but containingPΩ;
2) Finding the set of all minimal siphons of Σ excludingp2but containingPΩ∪{p1};
…
n) Finding the set of all minimal siphons of Σ excludingpnbut containingPΩ∪{p1,p2,…,pn–1};and
n+1) Finding the set of all minimal siphons of Σ containingPΩ∪{p1,p2,…,pn}=PΩ∪S.
The solutions to the aboven+1 sub-problems constitute the solution to the original problem.Consequently,the lemma holds.
Lemma 2:Let Σ=(P,T,F) be a PN,PΩbe a set of places,and Δ=(Σ,PΩ) be the problem of finding the set ΠΔof all minimal siphons containingPΩof Σ.It holds that
1) Σ=∅ ∨PΩ⊄P∨PΩis a siphon of Σ but not minimal=>ΠΔ=∅;
2) Σ ≠ ∅ ∧PΩ⊆P∧PΩis a minimal siphon of Σ=>ΠΔ={PΩ}.
Proof:Straightforward from the definition of minimal siphons.
Now,we are ready to prove the following result.
Theorem 1:Given a PN Σ as the input,Algorithm 1(IGPMSE) outputs the set of all minimal siphons in Σ.
Proof:We prove that the set Θ output by Algorithm 1 is the solution ΠΔto the problem Δ=(Σ,∅),i.e.,the set of all minimal siphons in Σ.
First,we compute (Σ,Θ)=HandleSourcePlace(Σ) and Σ=ReduceNetSize(Σ).Let Σ' be the updated net.By Results 1 and 2,it is


In the case thatm=0,i.e.,none of sub-problems are in Case 3,Θ is the final output set and it obviously holds ΠΔ=Θ.Otherwise,problems,,…,are further decomposed by repeating the above similar procedure.Note that during the procedure of iterative problem decomposition,the size of the considered net is gradually reduced.It implies that there cannot be infinite sub-problems that need to be further decomposed.Consequently,after the iterative problem decomposition and the update of Θ,the final set Θ=ΠΔ.
Finally,we note that the computational complexity of the proposed IGPMSE (Algorithm 1) is actually the same as that of GPMSE.This is because the tree generated by IGPMSE can be the same as the one generated by GPMSE in the worst case.Since GPMSE is of exponential complexity with respect to the net size [32],the computational complexity of IGPMSE is also exponential with respect to the net size.Nevertheless,although they have the same complexity,IGPMSE performs much better than GPMSE in computational time and memory consumption in most cases,which will be seen in Section V.
C.Illustrative Example
In this subsection,we illustrate the proposed IGPMSE by considering the computation of all minimal siphons in the PN Σ shown in Fig.1.
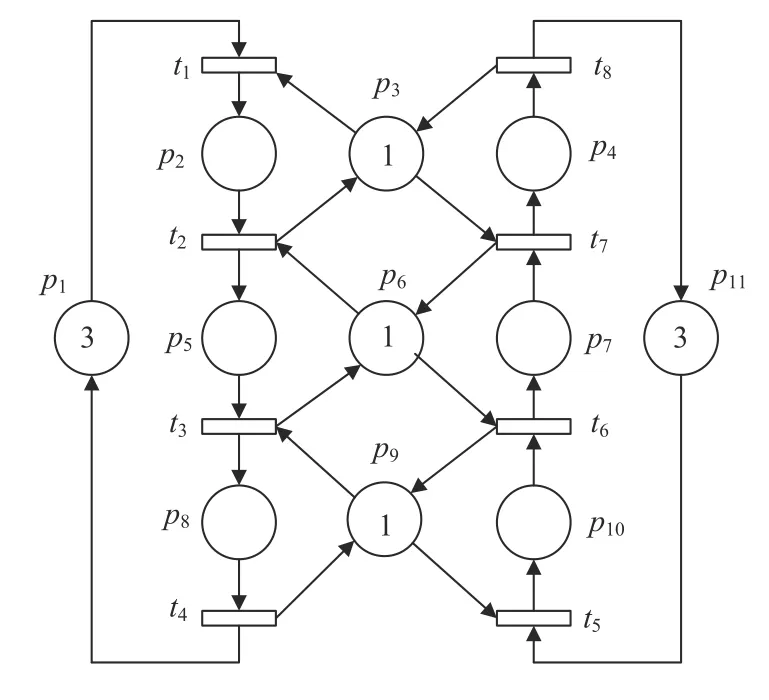
Fig.1.PN Σ.
First,functionsHandleSourcePlaceandReduceNetSizeare called to handle the PN Σ.We can see that it contains neither source nor sink nodes.Thus,we have Θ=∅ and Σ1=Σ after calling these two functions.(Here we use Σ1to denote the resultant net after calling these two functions.) Now,we create the root node Δ1=(Σ1,∅) of a tree,as shown in Fig.2.For the sake of simplicity,we use the setPiof places in a net Σito denote the net.For instance,the set of placesP1={p1−p11}denotes the net Σ1.Next,we get a minimal siphonS1={p8,p9,p10} by callingPomegaMiniSiphon(Σ1,∅) and we have Θ={S1},Γ[1]=S1and Γ[2]=∅.
Now,we start the decomposition of the problem Δ1=(Σ1,∅),which is performed by callingCreateNewNode(Σ1,∅,1,{S1}).Sinceindex=1,it means that we useS1=Γ[1]={p8,p9,p10} to decompose the problem.The details are as follows.Note that the depth-first search is adopted to iteratively decompose problems.
First,we consider the case that placep8is deleted from the net Σ1.FunctionReduceNetSizeis then performed to simplify the net.The obtained net is denoted as Σ2withP2={p2−p7,p10,p11} .Accordingly,a new node Δ2=(Σ2,∅)is added to the tree with an arc labeled by “p8” from node Δ1=(Σ1,∅).
Now,we decompose the problem Δ2=(Σ2,∅) by callingCreateNewNode(Σ2,∅,2,{S1}).Since Γ[2] is empty,we compute a minimal siphonS2={p5,p6,p7} by callingPomegaMiniSiphon(Σ2,∅) and use it to decompose the problem Δ2=(Σ2,∅).Note that it is now updated that Γ[2]=S2,Γ[3]=∅ and Θ={S1,S2}.
Similarly,we first consider the case that placep5is deleted from the net Σ2,resulting in a new node Δ3=(Σ3,∅) in the tree with an arc labeled by “p5” from node Δ2=(Σ2,∅),where Σ3is a net with the set of placesP3={p2−p4,p7,p10,p11}.
Again,we decompose the problem Δ3=(Σ3,∅) by callingCreateNewNode(Σ3,∅,3,{S1,S2}).By a similar procedure,we compute a minimal siphonS3={p4,p7,p10,p11} to decompose the problem Δ3=(Σ3,∅) and it is updated that Γ[3]=S3,Γ[4]=∅ and Θ={S1,S2,S3}.
When we consider the first case that placep4is deleted from the net Σ3,we obtain an empty net.Hence,we consider the second case that placep7is deleted from the net Σ3and it is required thatp4is included in minimal siphons to be found.In this case,we derive a new node Δ4=(Σ4,PΩ) in the tree with an arc labeled by “p7” from node Δ3=(Σ3,∅),where Σ4is a net with the set of placesP4={p2–p4} andPΩ={p2–p4}derived by expanding the set {p4}.It is verified thatPΩ={p2–p4} is a siphon and thus Δ4=(Σ4,PΩ) does not need to be further decomposed.It is verified thatPΩ={p2–p4} is not a minimal siphon and thus we do not update the set Θ.Then,we consider the third case that placep10is deleted from the net Σ3and it is required thatp4andp7are included in minimal siphons to be found.Similarly,a new node Δ5=(Σ5,PΩ) is generated in the tree with an arc labeled by “p10” from node Δ3=(Σ3,∅),where Σ5is a net with the set of placesP5={p2–p4} andPΩ={p4,p7}.Δ5=(Σ5,PΩ) does not need to be further decomposed becausePΩ⊄P5.Finally,we consider the fourth case thatp11is deleted from the net Σ3but it is required thatp4,p7,p11are included in minimal siphons to be found.Similarly,a new node Δ6=(Σ6,PΩ) is generated in the tree with an arc labeled by “p11” from node Δ3=(Σ3,∅),where Σ6is a net with the set of placesP6={p2–p4} andPΩ={p4,p7,p10}.Δ6=(Σ6,PΩ) does not need to be further decomposed as well becausePΩ⊄P6.
Now,the decomposition of the problem Δ3=(Σ3,∅) is finished.It is Θ=CreateNewNode(Σ3,∅,3,{S1,S2})={S1,S2,S3}.We then go back to consider the second case of decomposing the problem Δ2=(Σ2,∅),i.e.,placep6is deleted from the net Σ2and it is required thatp5is included in minimal siphons to be found.In this case,a new node Δ7is generated in the tree.
By repeating the above similar procedure,we may obtain nodes Δ8,Δ9,…,Δ17one by one,resulting in the tree shown in Fig.2.The final set Θ computed by IGPMSE is Θ={S1–S7},which means that the set of all minimal siphons of the net in Fig.1 is {S1–S7}.The details ofS1–S7can be found in Fig.2.
We notice that we use colored nodes to indicate those problems that do not need to be further decomposed.In particular,red nodes imply thatPΩis a siphon but not minimal;yellow nodes imply thatPΩis a minimal siphon;black nodes imply thatPΩ⊄P.
V.COMPARISON
In this section,we compare the performance of the proposed IGPMSE and the original GPMSE in [32].Note that,although many new methods are proposed after GPMSE for computing minimal siphons in PN,most of them are applicable to a specific class of PN only.Thus,although they might have higher computational efficiency than our proposed method,ours has the advantage of having no restriction on the class of PN.On the other hand,concerning methods in the literature applicable to any class of PN,to our best knowledge,the methods proposed by Cordoneet al.[32] are still the most efficient methods among them.As a result,we compare the proposed method (IGPMSE) with the GPMSE [32] only in the paper.
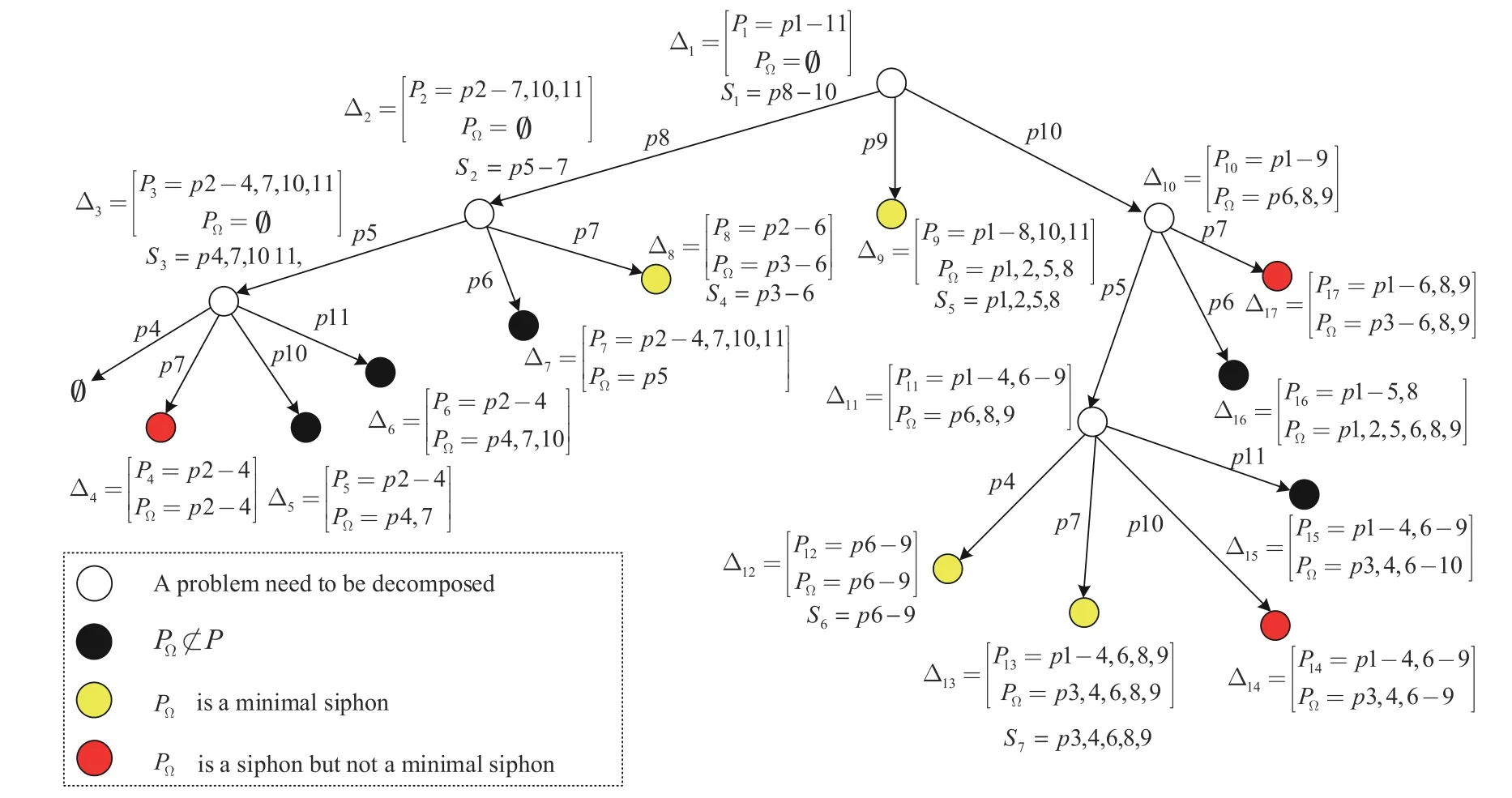
Fig.2.Tree generated by IGPMSE.
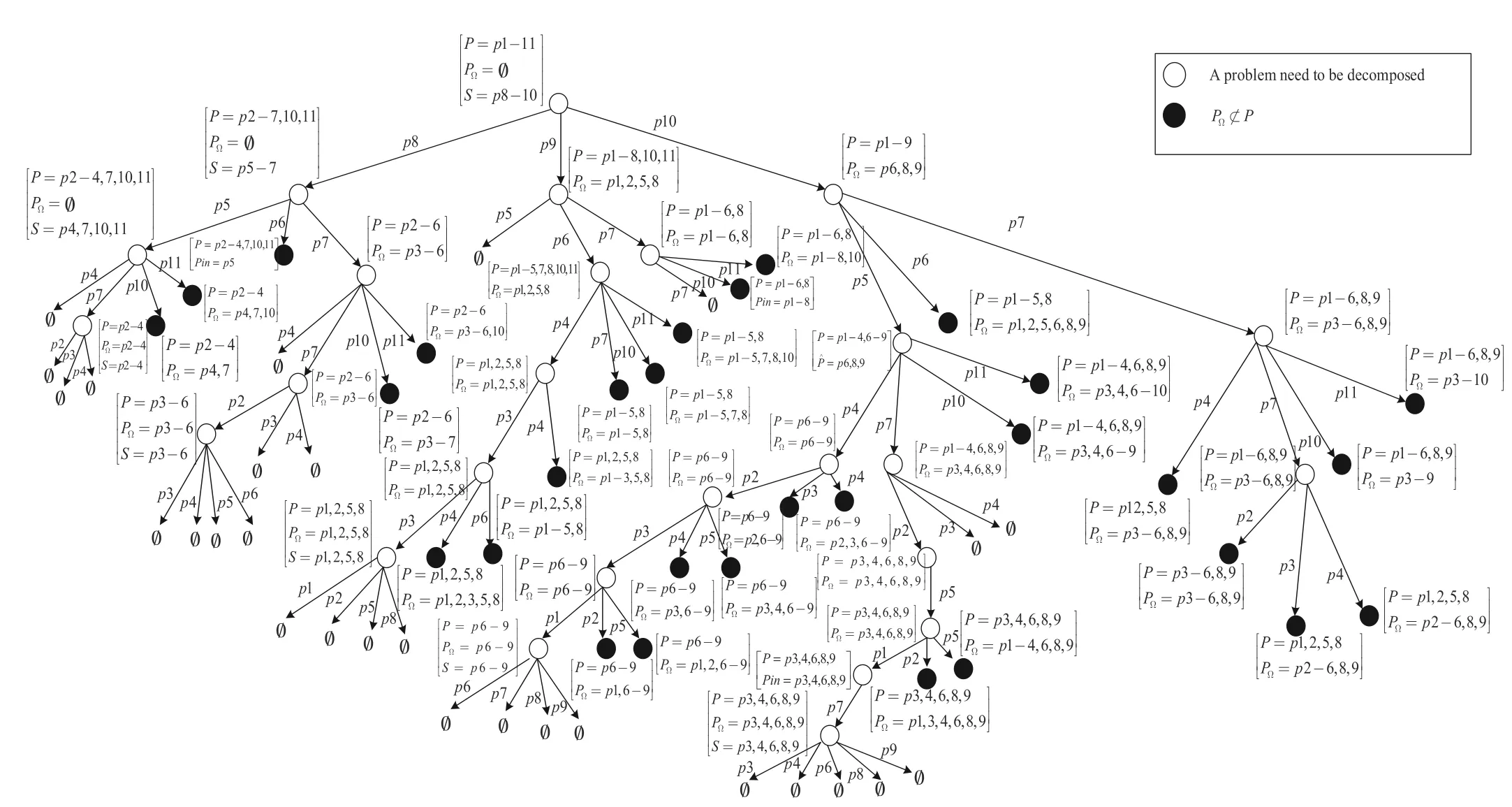
Fig.3.Tree generated by GPMSE in [32].
First,we make the comparison by applying them both to the PN in Fig.1.We have already obtained the tree generated by using IGPMSE,as shown in Fig.2.Now,we construct the tree by using GPMSE,which is presented in Fig.3.It is clear that the tree generated by IGPMSE is much simpler than that generated by GPMSE.In Table I,we provide more details to compare them.In particular,the number of nodes of the tree is listed in the 2nd column;the number of nodes where a problem needs to be decomposed is listed in the 3rd column;and the last column shows the maximum number of nodes that need to be saved in memory during the construction of the tree(considering the depth-first search).We note that the computational time is closely related to the number of nodes of the tree and the number of nodes that need to be decomposed,whereas the memory consumption depends on the maximum number of nodes that need to be saved during computation.Thus,according to Table I,we may see that IGPMSE performs better than GPMSE when applied to the PN in Fig.1,both in terms of computational time and memory consumption.
Next,in order to further validate the advantage of IGPMSE over GPMSE,we developed a tool,written in C++,to implement three methods,namely,GPMSE,GPMSE using the depth-first search,and IGPMSE.The readers can download this tool from [34].Using this tool,we carry out an experiment where we enumerate the minimal siphons in a series of PNs with the net sizen(i.e.,the number of places and transitions) ranging from 31 to 42.For every net size,we consider 100 nets that are randomly generated withdi=do=0.05,wherediis the probability of having an arc going fromany place to any transition anddois the probability of having an arc going from any transition to any place.The experiment was performed in the environment with Intel Processor at 2.53 GHz and 3 GB memory under Windows 7 operating system.

TABLE ICOMPARISON RESULTS OF GPMSE AND IGPMSE APPLIED FOR THE ENUMERATION OF MINIMAL SIPHONS IN THE PN IN FIG.1
We found that GPMSE fails to get a result for any of such net sizes (i.e.,n=31,32,…,42) due to running out of memory.In contrast,both GPMSE using the depth-first search and IGPMSE can get results.We thus provide the experimental results from these two approaches in Fig.4,where we show the average CPU time (over the 100 simulations) versus the net size and we use a blue line to denote GPMSE with the depth-first search and a red line to denote IGPMSE.Fig.4(a) provides the results for all the considered net sizes.We may see that the computational time of GPMSE with the depth-first search grows exponentially and reaches more than 100 seconds whenn=42,whereas our method (IGPMSE) costs less than 10 seconds in all cases.Also,we provide a closer zoom in Fig.4(b) of those results fornfrom 34 to 37,which again shows the superiority of IGPMSE over GPMSE with the depth-first search.
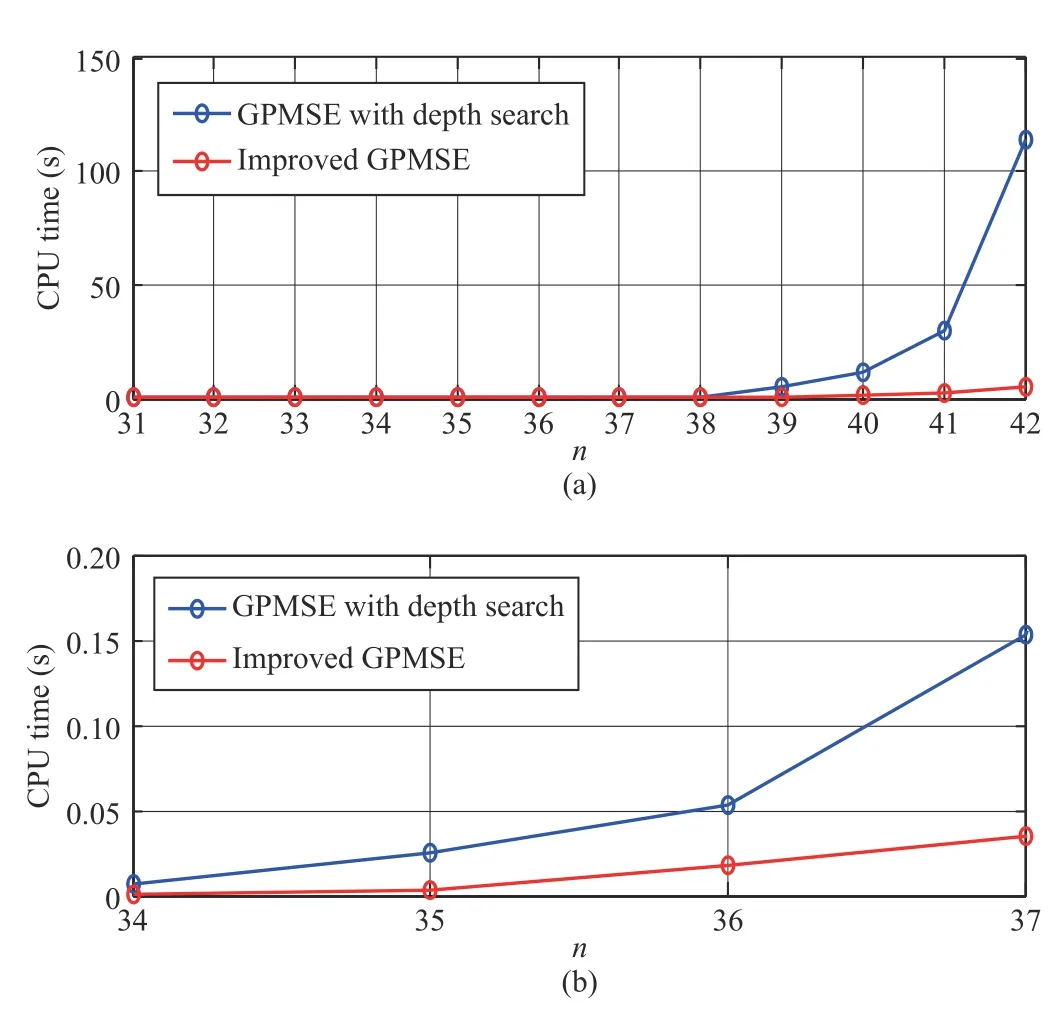
Fig.4.Experimental results of the application of GPMSE with the depthfirst search and IGPMSE.(a) The average CPU time versus the net size n from 31 to 42;(b) A closer zoom of the results in Fig.4(a) for the net size n from 34 to 37.
From this experiment,we conclude that IGPMSE consumes less memory than GPMSE.Also,we argue that IGPMSE behaves better than GPMSE in computational time,which becomes more evident when the size of the handled net grows.
We conclude this section by mentioning another approach in[35] that computes minimal siphons based on the problem decomposition as well.We note that the approach [35] applies to S3PR only,whereas the proposed IGPMSE applies to arbitrary PNs.
VI.CONCLUSIONS AND FUTURE WORK
This paper improves an algorithm for the minimal-siphon computation developed in [32],i.e.,the algorithm of global partitioning minimal-siphon enumeration (GPMSE).It should be evident from the above discussions that the improved algorithm,namely IGPMSE,provides a tractable decomposition of such a problem.Through the application of several PNs,it is shown that IGPMSE has lower computational complexity and,more importantly,the memory consumption has been reduced significantly by employing the depth-first search.Thus,the proposed IGPMSE constitutes an important step to tackle with minimal-siphon computation in large nets.
Similar improvements can also be made on local partitioning minimal-siphon enumeration (LPMSE) developed in [32],which is left as our future work.In addition,other directions for further research include:1) Finding more constraints that could further reduce the number of problems in the problem list;and 2) Establishing complete algorithms for supervisory control problems.Furthermore,we may consider the use of parallel computing so that the subproblems can be solved concurrently.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Sampling Methods for Efficient Training of Graph Convolutional Networks:A Survey
- Fault Accommodation for a Class of Nonlinear Uncertain Systems With Event-Triggered Input
- Precise Agriculture:Effective Deep Learning Strategies to Detect Pest Insects
- Maximizing Convergence Speed for Second Order Consensus in Leaderless Multi-Agent Systems
- Exponential Set-Point Stabilization of Underactuated Vehicles Moving in Three-Dimensional Space
- An Adaptive Rapidly-Exploring Random Tree
