Aerodynamic Effects Compensation on Multi-Rotor UAVs Based on a Neural Network Control Allocation Approach
2022-01-25SarahMadrugaAugustoTavaresSauloLuizTiagodoNascimentoandAntonioMarcusLimaSenior
Sarah P.Madruga,Augusto H.B.M.Tavares,Saulo O.D.Luiz,Tiago P.do Nascimento,,and Antonio Marcus N.Lima, Senior
Abstract—This paper shows that the aerodynamic effects can be compensated in a quadrotor system by means of a control allocation approach using neural networks.Thus,the system performance can be improved by replacing the classic allocation matrix,without using the aerodynamic inflow equations directly.The network training is performed offline,which requires low computational power.The target system is a Parrot MAMBO drone whose flight control is composed of PD-PID controllers followed by the proposed neural network control allocation algorithm.Such a quadrotor is particularly susceptible to the aerodynamics effects of interest to this work,because of its small size.We compared the mechanical torques commanded by the flight controller,i.e.,the control input,to those actually generated by the actuators and established at the aircraft.It was observed that the proposed neural network was able to closely match them,while the classic allocation matrix could not achieve that.The allocation error was also determined in both cases.Furthermore,the closed-loop performance also improved with the use of the proposed neural network control allocation,as well as the quality of the thrust and torque signals,in which we perceived a much less noisy behavior.
I.INTRODUCTION
IN the last decade,there has been a substantial growth in the usage of unmanned aerial vehicles (UAV) in a series of applications [1].They are widely used to perform difficult or dangerous missions,military ones [2],or to make civilian tasks more efficient,like package delivery.The research of modeling and control techniques for this type of vehicles,especially the quadrotors,has also grown considerably [1].A quadrotor dynamic model is usually an under-actuated nonlinear system [3].Quadrotor UAVs are considered classic unstable dynamical systems [4],hence,the study of suitable algorithms to improve stability and reduce the influence of disturbances is indispensable.
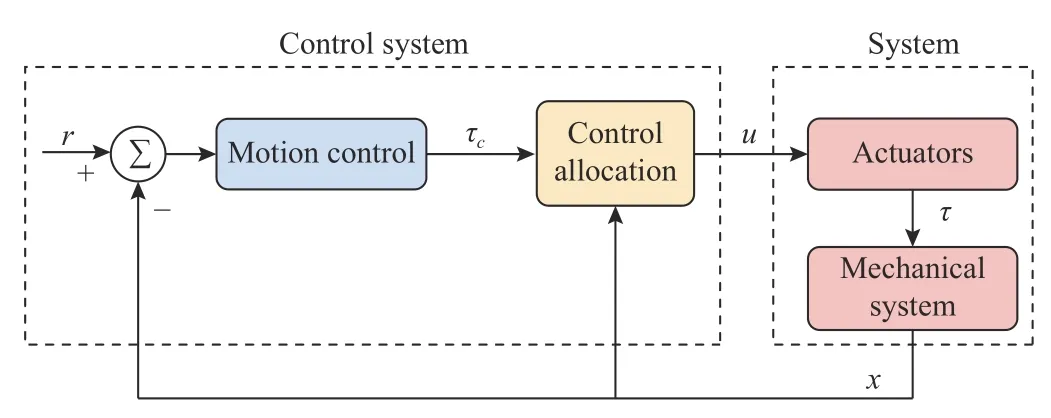
A control allocation algorithm aims at computing a control input that ensures that the commanded virtual control is produced by the set of effectors and actuators at all times.This objective would fail to be met if the commands require forces beyond the capabilities of the actuators due to saturation or other physical limitations such as aerodynamic effects [5].
The use of control allocation offers the advantage of a modular design where the motion control algorithm can be designed without detailed knowledge about the actuators.Issues such as input saturation,rate constraints,actuator fault tolerance,power efficiency,etc.,could be managed within the control allocation algorithm [5].The resulting control laws specify which total control effect to produce but not how to produce it,and hence the need for control allocation arises [6].
Conventional multirotor UAVs have the rotors in parallel directions to collectively counteract gravity and optimize flight time.Consequently,these aircrafts have under-actuated dynamics due to the coupling between the horizontal translational and rotational dynamics [7].As a result,the control of a quadrotor tends to present a high sensibility when subjected to an input constraint [8].Therefore,control allocation is necessary for setting suitable commands for each rotor,so that it generates the desired control effect,that is,the forces and torques,while presenting an acceptable performance and respecting the constraints imposed by the minimal and maximal angular velocities and hence the maximum and minimum forces and torques [8].
In the classic quadcopter modeling used for most control techniques,the control allocation is often performed through the control effectiveness matrix,usually named mixing matrix or allocation matrix.It provides an invertible relation between mechanical conjugates and motor rotation speeds.This matrix results from a model simplification that neglects important aerodynamic effects that influence thrust forces and torque behavior,especially regarding small aircraft or aggressive maneuvering [9].As a matter of fact,this negligence leaves the quadcopter subject to saturation,and the torque and thrust commands sent by the controller are not properly generated by the actuators,because the motors cannot achieve the necessary rotation speed.
In this sense,a new control allocation method was proposed to consider aerodynamic effects,most notably those regarding blade flapping and inflow effects as described in [10],based on a function fitting neural network to replace the classic mixing matrix.This method allows us to improve the controller performance without the need for directly using aerodynamic effects equations in the control algorithm or the allocation problem.Furthermore,network training is performed offline,and the in-flight control allocation depends only on the virtual control inputs and some state-space variables,which will be detailed further in this paper.
While it is true that there are several results regarding UAV control in the literature,we did not find works approaching the problem of the error inserted by the disregard of aerodynamic effects in the control allocation,which is the target of this paper.Even the robust controllers available in the literature and mentioned in the next section,still use the classic mixing matrix,forcibly inserting an error in the rotation speeds established at the motors and hence in the control performance.
Thus,themain contributionsof this paper are:
1) We propose the use of a classic neural network as anovel control allocation approachthat takes into account the aerodynamic effects.
2) The proposed method can be used toimprove the performance of quadrotor controllers in general,since it removes the error introduced by the classic allocation matrix.
3) Our experimental results verified thatneglecting aerodynamic effects in the control allocation has a direct negative impactin the flight performance;
4)Several aspects of the system were improvedwith the new control allocation,including the decrease in the allocation error,the increase in the controller performance,and a better overall signal quality.
II.RELATED WORK
Dynamic models with minimum complexity for quadrotors are well documented in the literature [11].These models generally use six-degree-of-freedom (6-DOF) rigid-body equations and a highly simplified rotor dynamics as a function of the square of motor speed.The treatment of quadcopter dynamics around steady-state conditions has often ignored rotorcraft aerodynamic effects due to its complex physical modeling [12].In certain circumstances similar to hover flight,these effects could be neglected.Nevertheless,they can prove to be very relevant during agile maneuvers [9] or in the case of small aircrafts [13],[14].Davis and Pounds [13]sought to understand and exploit the aerodynamic effects acting on a small-scale quadrotor to regulate relative position,attitude,and velocity without extrinsic sensors.Ninget al.[14] investigated the aerodynamics and aeroacoustics of propellers for small unmanned aerial vehicles.Powerset al.[15] demonstrated that the dynamic response and performance of a micro UAV are greatly influenced by its aerodynamics,and the introduction of these effects into controllers is also discussed.They show that the controller performance can be improved when considering aerodynamic effects into the model.
Poundset al.[16],[17] have included some aerodynamic effects modeling in the rotor dynamics equations to enhance model accuracy.The authors adopted a generalized flapping dynamics structure,based on helicopter theories,to model the rotor flapping phenomenon.Bristeauet al.[18] studied the aerodynamic role of the propellers.Hoffmanet al.[19] and Huanget al.[9] modeled aerodynamic effects associated with blade flapping,airflow distribution,and thrust generation,to derive a model that can cover extreme maneuvers.
Caiet al.[11] introduced a frequency-domain modeling methodology that can be applied to various multi-rotor aerial vehicles.Niemiec and Gandhi [20] created a dynamic simulation for a 2 kg quadcopter,where several inflow models were used to analyze the behavior of the aircraft in trim,in hover,and forward flight.Kantue and Pedro [12],[21] used a radial basis functions neural network (RBF-NN) for model identification of an unmanned quadcopter in accelerated flight to estimate rotor dynamics parameters from an unknown flapping dynamics model.
The works presented above are mainly about modeling the aerodynamic effects that impact multirotor aircraft systems.However,the literature is still lacking in regard to techniques to actually take these effects into account in the quadrotor system,especially when it comes to the control allocation,which none of the previous works mention.
Omariet al.[22] present the design and evaluation of a nonlinear control scheme for a six-rotor helicopter that takes the first-order drag effects into account explicitly,and a hierarchical nonlinear controller is designed to actively compensate for the nonlinear effects caused by these drag forces.Note that,even though a dynamic model including the blade flapping and induced drag forces is presented in this paper,the corresponding traditional mixing matrix for a sixrotor helicopter is still employed by the authors.Even if the controller takes into account the drag forces,the control allocation completely neglects their existence,jeopardizing some of the controller’s performance when converting its commands to the actuators’ rotation speeds.
Chebbiet al.[23] use a polynomial regression to obtain the control allocation of a coaxial multirotor.However,the problem the authors are trying to solve in this work differs from the one we attack in our paper.They try to estimate a model that will solve the interference between the propellers in a pair of coaxial motors.Again,even though they estimate a thorough model of the actuators’ nonlinear effects,they neglect them in the control allocation.
Johansen and Fossen [5] and Alves [8] present the fundamentals of control allocation theory.A survey regarding different control allocation algorithms and applications to aerospace,maritime,automotive,and other application areas is presented in [5],while the applications of several methods of control allocation to an experiment with a differential-drive mobile robot and simulations of a quadrotor UAV and a Remotely Operated Underwater Vehicle are presented in [8].
Most recently,the interest in control allocation applied to multirotor vehicles has increased,given the rise in the usage of this type of aircraft.Kirchengastet al.[24] showed the comparison of different control allocation techniques,as well as Alves [8],but this time they are applied to a laboratory setup which emulates the rotational dynamics of a quadrotor,though not to a real quadcopter.Monteiroet al.[25] also analyzed control allocation algorithms to countermeasure saturation in the actuators,however,they generalized the classic direct control allocation (DCA) to suggest new methods,called partial control allocation (PCA) [25].
Doman and Oppenheimer [26] stated that forces and moments produced by the vehicle’s aerodynamic control surface are often nonlinear functions and that this limits most control allocation algorithms applications,since they are based on the assumption that the control variable rates are linear functions.The authors then presented a mixed optimization control allocation scheme that minimizes the norm of the error and the deviation of the control input from a preferred value,to attack the inaccuracies introduced by these linear assumptions.
In addition,Smeuret al.[27] dealt with the problem of actuator saturation for Incremental nonlinear dynamic inversion (INDI) controlled flying vehicles.The authors integrated the Weighted Least Squares optimization-based control allocation algorithm into INDI,which allows for prioritization among roll,pitch,yaw,and thrust.The conventional application area for control allocation algorithms is over-actuated mechanical systems,however,the principles of control allocation are general and can be applied to underactuated systems subject to saturation and nonlinear effects.
The main technique most control allocation algorithms have in common is solving a constrained optimization problem[28],and this process is usually performed on-line [29],requiring computational resources from embedded systems[5].Even though their computational complexity is mostly within the capabilities of today’s computer technology,some works highlight the advantages of requiring a low computational power on-line [30] such as the method we propose in this paper.
The control allocation theory establishes that it can be used to treat actuator saturation problems or other disturbances which may affect their optimal functioning [5].However,at the moment of this research,there are no works proposing to specifically compensate aerodynamic effects inside the control allocation,replacing the traditional control effectiveness matrix and thus mitigating the allocation error.
Neural networks have been receiving wide attention in the control field,being proposed especially for identification and control of nonlinear dynamic plants [31].A common application of neural networks to controllers is as an adaptive element to dynamic inversion plants,as stated by Caoet al.[32],Jianget al.[33],and Wanget al.[31].Likewise,Ansariet al.[34],[35] employed a baseline controller with a dynamic inversion in the inner loop for attitude tracking and body rates stabilization,with the addition of a Radial Basis Function Neural Network to estimate the unknown attitude dynamics of the quadrotor.
According to Achermannet al.[36],small UAVs are particularly susceptible to wind drag because of their relatively low mass and their operation at low altitudes where the wind environment can be more complex.The authors proposed an approach for predicting high-resolution wind fields using a deep convolutional neural network to generate 3D wind estimates.In a similar topic,Shiet al.[37] presented a deep-learning-based robust nonlinear controller called Neural-Lander that improves control performance of a quadcopter during landing,since near-ground trajectory control is difficult for multi-rotor drones,due to the aerodynamic effects caused by interactions between multirotor airflow and the environment.Verberne and Moncayo[38] described the design of an extension of the Nonlinear Dynamic Inversion control architecture for wind disturbance rejection in quadrotor UAVs,followed by the application of adaptive artificial neural networks to correct inversion errors caused by wind disturbance.
Neural networks have also been used for fault-tolerant control design in quadcopters,as in the works of Abbaspouret al.[39] and Songet al.[40].The former used a neural network adaptive structure for fault detection and isolation combined with a nonlinear dynamic inversion technique to compensate for faults in the actuators,while the latter combined the radial basis function neural networks with virtual parameter estimating algorithms to develop an indirect neural network-based adaptive fault-tolerant control scheme.Finally,Reddinger and Gandhi [41] trained a predictive neural network to estimate power as a function of the redundant control settings for a range of flight speeds for a compound helicopter.This neural network is used as a surrogate model for a gradient-based optimization to allocate the redundant control settings with a minimized power requirement.
Note that even though neural networks are used to identify aerodynamic models,the application of a neural network to perform the control allocation of a quadrotor control system is still uncommon in the literature,specially considering aerodynamic effects,which is an application our research did not find in the most relevant works in this area of study.
III.MODELING AND CONTROL OF A QUADCOPTER
The traditional quadrotor model assumes that the aircraft is built as a rigid structure,usually in form ofX,with four arms,as shown in Fig.1,where the axis convention used in this paper is presented.The angles use the Tait-Bryan convention,where the movement of rotation around thex-axis is calledrolland is represented in this paper by the angle φ.Therollmotion induces a linear displacement of the aircraft to the sides.The rotation around they-axis is calledpitch,represented by the angle θ,and causes a linear displacement in the forward or backward direction.The rotation around thezaxis is calledyaw,represented by the angle ψ.The torques that induce each one of these motions are here called τφ,τθ,τψ,respectively.The force that enables the drone to move upwards is thethrustT.Ideally,it would only have one vertical component in thez-axis.
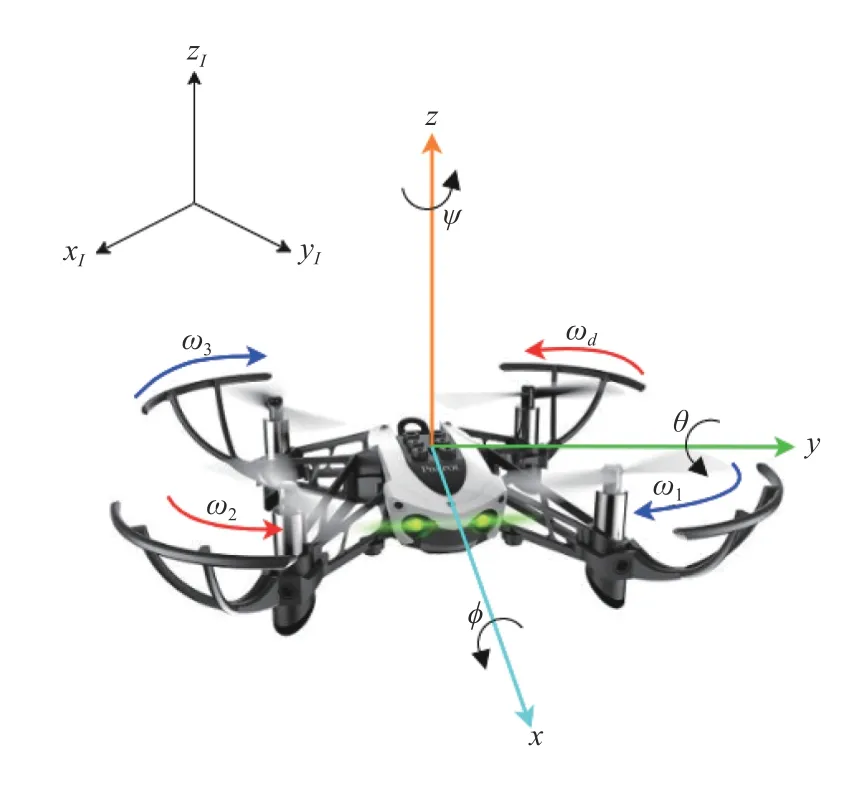
Fig.1.In the front,we show the axis configuration in the local frame,as well as the rotation sense for each rotor and the roll (φ),pitch (θ),yaw (ψ)notations used in the quadcopter model.In the back,there is the axis configuration in the inertial frame.
Since our system is under-actuated,a control allocation algorithm is needed to send the appropriate commands to the actuators.The controller commands virtual control inputs [5]for theroll,pitch,andyawtorques,as well as thethrustforce.The control allocation then transforms these mechanical conjugates into angular velocities commands for the four motors.
Table I shows the influence of the angular velocities of the motors in the resulting motion of the aircraft.Here,ωi,i=1,2,3,4,is the angular velocity of each rotor.An upward arrow means an increase in the velocity of a specific motor,while a downward arrow corresponds to a decrease in velocity.Note that the arrows can be inverted for a change of direction of motion.
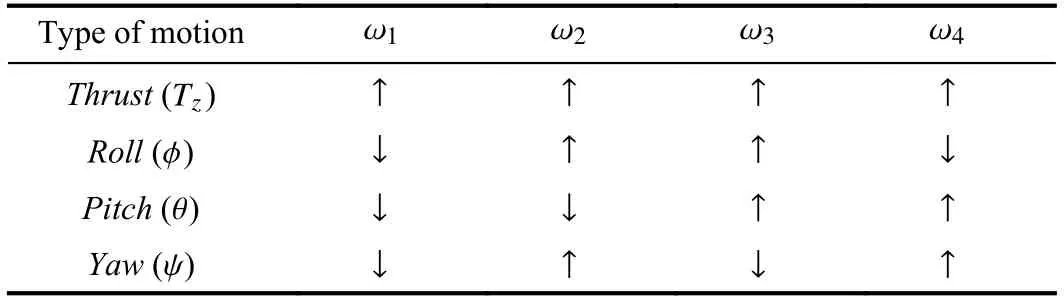
TABLE IROTOR SPEED INFLUENCE ON QUADCOPTER MOTION
A.Method Overview and Notation
In our control allocation,the objective is to produce actuator commands that will generate resultant torques and thrusts on the UAV body as close as possible to the requested control signals,also called virtual control inputs.In this sense,we provide here an overview of the notations used throughout this paper,for better understanding of the upcoming sections.
Definition 1:The virtual control inputsare the commanded signals at the output of the controller,where T represents the thrust force,and τ,the torques.
Remark 1:In each of the four actuatorsi,i=1,2,3,4,there are the body-frame thrusts,and torques,τi∈R3,as well as their componentsrespectively.
Definition 2:u=[ω1ω2ω3ω4]T∈R4is the vector of angular velocities sent as actuator commands by the control allocator.These velocities should produce the desired res ultant thrustandtorques.
Definition 3:The vector[T,τ]=[Tτφτθτψ]T∈R4represents the real resultant mechanical conjugates established at the UAV body.In this paper,they were calculated by means of experimental data and dynamic model equations.Again,T represents the thrust force,and τ,the torques.
Assumption 1:IfFis a virtual function that describes the transformation of the actuator commands ωito real thrust and torques,andF~is its model,we have

Hence,the desired control allocation must perform the inverse operation,using the virtual control inputs

Using this notation,the control allocation algorithm goal is to achieve T=Tcand τ=τc.Havingthe composition of the inverse mappings with the real system behaviour functions must be equal to identity [23].See Fig.2.
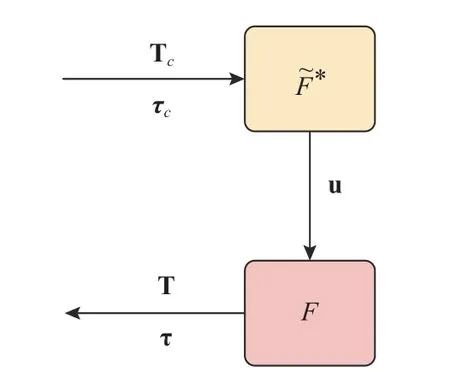
Fig.2.Data flow from the virtual control inputs T c,τc to the real mechanical conjugates applied on the UAV body T,τ .can represent the control allocation block.
Remark 2:can be interpreted as the control allocator.In this paper,it can refer to the classic mixing matrix or the proposed neural network,and we will compare the performance of both methods.
Remark 3:represents the quadcopter dynamic model considering aerodynamic effects such as blade flapping and will be further detailed in Sections III-B and III-C of this paper.
B.Quadcopter Model
The dynamic and kinematic behaviors of the UAV can be described by the following equations [42]:
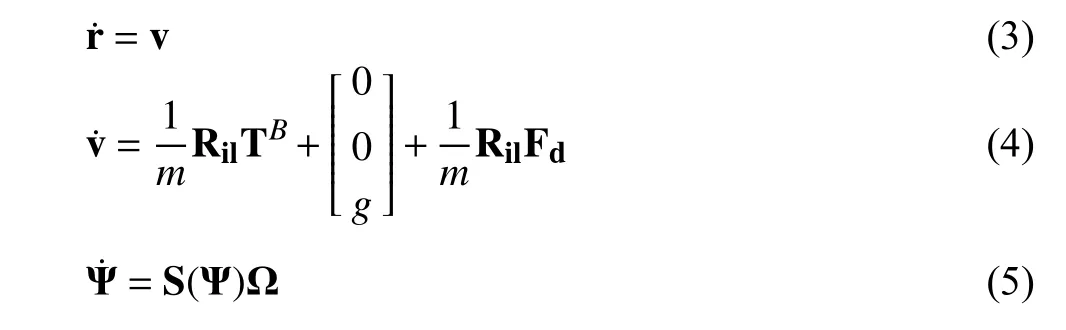

wherec(·) is the cosine ands(·) is the sine of the angle.
S(Ψ) is the coupling matrix,expressing an interconnection in the system’s angle change,and it is given by
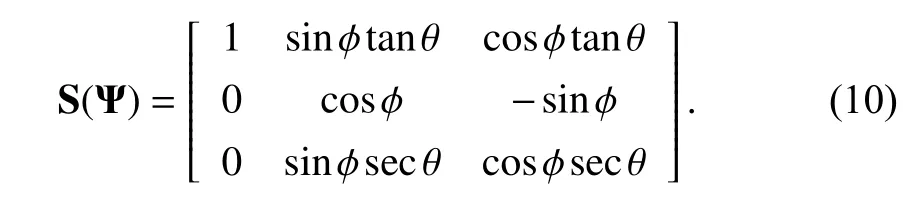
C.Aerodynamic Effects
There are several aerodynamic and gyroscopic effects that can modify the force model introduced in (3)–(6),the most important of them being the ones calledblade flappingandinduced drag,which are of significant importance in understanding the natural stability of quadrotors.These effects are particularly relevant because they induce forces in thex-yrotor plane of the quadrotor,precisely the under-actuated directions in the dynamics that cannot be easily dominated by high gain control [43].
While disturbances caused by drag forces are already included in the basic model in (4) as an additive term,the inclusion of blade flapping equations is not so straightforward.This phenomenon is caused by the flapping effect generated in the blades of the propellers by horizontal translation of the rotor in the air.During the translation of the rotor,one blade (called theadvancing blade) will move in the direction of translation,while the other (theretreating blade)will move opposite to the direction of motion.The net velocity of the advancing blade will increase,and that of the retreating blade will decrease with respect to the air.This creates a disparity of lift between the advancing side of the rotor and the retreating side of the rotor (see Fig.3) [17].
According to Poundset al.[17],a rotor blade balances the lift imbalance (aerodynamic force),centripetal force,and blade weight force by allowing free rotation around a hinge or flexure,and this is known as rotor or blade flapping.The advancing blade will rise,the retreating blade will fall,as in Fig.3,and therefore the rotor plane will tilt in an effort to meet a new equilibrium.Increasing translational velocity leads to increasing rotor tilt.When the rotor plane tilts,the thrust force generated by the blades is correspondingly tilted,resulting in a horizontal component that opposes the direction of translation.
Allowing the rotor blade to bend is very important in the mechanical design of the quadcopter.A rotor that is too rigid can cause transmission of these aerodynamic forces directly through to the rotor hub and may result in a mechanical failure of the motor mounting or the airframe itself [43].Leishman[44] also states that if the rotor disc is perfectly rigid,the helicopter will flip,as was the case in early experiments.
As aforementioned,rotor flapping causes the rotor plane to tilt and hence the thrust force will also be tilted and will have a horizontal component.The total thrust TBthat appears in (4)results from the sum of the thrustsproduced by each of the four propellersi=1,2,3,4 [10]

The constant γaero=ρa0cR/Ibis the non-dimensional Lock Number [19],[44],which can be viewed as a measure of the ratio of aerodynamic forces to inertial forces.Here,Ibis the moment of inertia of the blade about the hinge,cis the chord of the blade,R=d/2 is the rotor radius,ρ is the density of air,anda0represents the slope of the lift curve per radian[19],[17].For a typical helicopter rotor,the value of the Lock Number varies from 5 to 10 [44].In the case of our minidrone,it is 0 .6051,as detailed in Table III.
Finally,the vector of torques τ=[τφτθτψ]Tacting on the body-frame of the drone can be calculated as
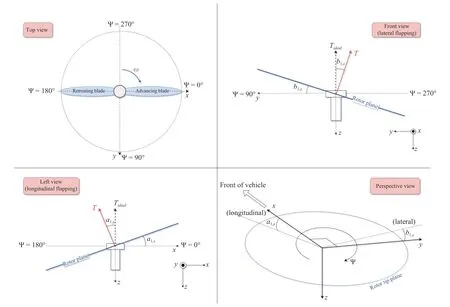
Fig.3.Perspective views of a rotor during flight.Longitudinal and lateral blade flapping angles are a1,s and b1,s,respectively,and Ψ here is the blade rotation azimuth angle.
AERODYNAMIC EFFECTS ON TOTAL THRUSTTABLE II

AERODYNAMIC EFFECTS ON TOTAL THRUSTTABLE II
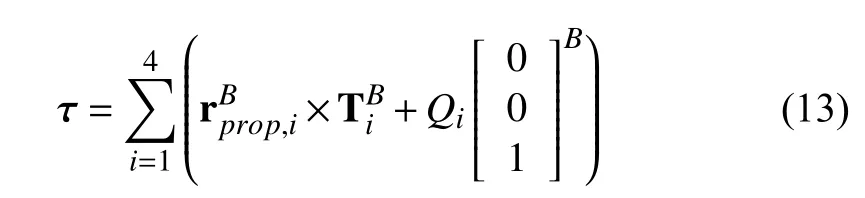
whereQi=αQωi|ωi| is the propeller-drag-induced torque [10].Note that,in (13),is as in (12) and is dependent on aerodynamic effects,since all the terms multiplied by the Lock Number γaerocome from aerodynamics [44],as is the case withb1,s,ianda1,s,i.Hence,the vector of torques τ will likewise be influenced by the aerodynamic effects.Appendix presents a more thorough calculation of the thrust rotation caused by aerodynamic effects,which also provides an alternative manner to visualize the thrust equation.

TABLE IIICONSTANTS SHOWN IN TABLE II
These aerodynamic effects are neglected in most models,assuminga1,s,i=b1,s,i=0 and ignoring the ratio of aerodynamic forces to inertial forces.Therefore,in those cases,the thrust vectors are supposed to be fully aligned with the body-framez-axis and do not have horizontal components caused by blade flapping.The anglesa1,s,iandb1,s,icannot be zero,as explained above,after all the rotor bend is essential to the quadrotor design.Since increasing translational velocities increases rotor tilt,aggressive maneuvering is specifically subject to the consequences of ignoring rotor flapping,as well as small aircrafts,as referenced in Section I.In this paper,we aim to compensate for the described aerodynamic effects using control allocation,without the need to include them in the control algorithm itself.
Overlooking these effects results in≈[0 0Ti]Tand

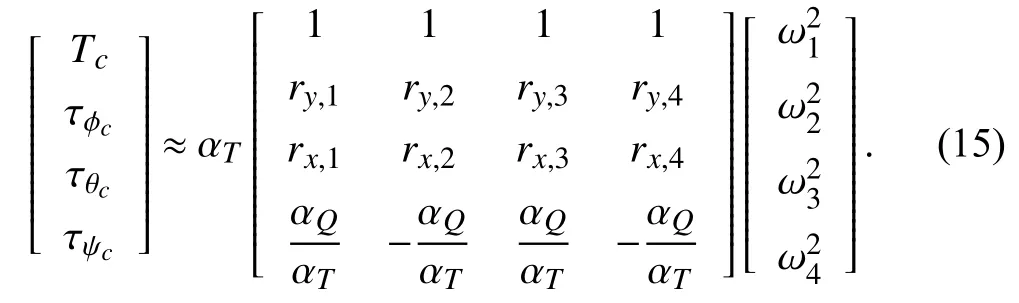
Definition 4 (Mixing Matrix Control Allocation (MMCA)):The control allocation performed by means of a matrix that provides an invertible relation between squared motor speeds and the plant input,as in (15),provided that the matrix is non-singular and the angular velocities ωiare not saturated.
If we write (15) as
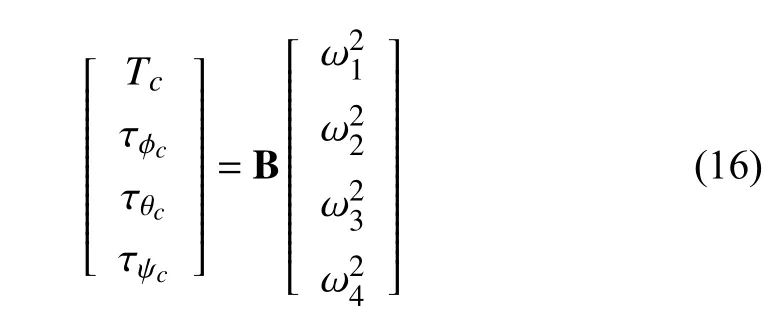
the angular velocities would then be determined as
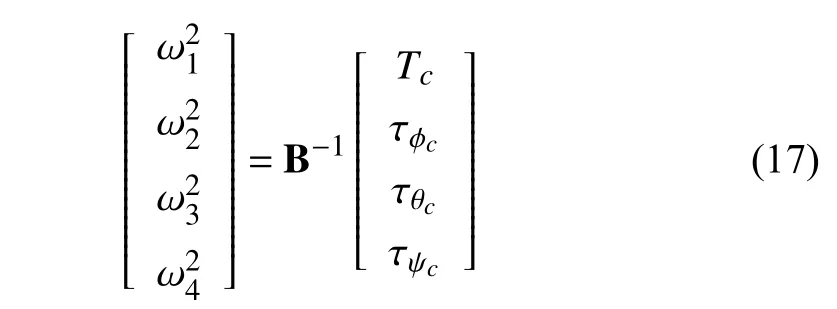
where B is the aforementioned control effectiveness matrix,mixing matrix,or allocation matrix.
Remark 4:Assuming the angular velocities ωiare not saturated is actually a very bold assumption when dealing with quadrotor systems [8].Also,with (11) and (13),obtaining the analytical inversionthat transforms the virtual thrust and torques [ Tc,τc] into the angular velocitiesωiwould be much more complex than in (17).That is the reason why this simplification disregarding aerodynamic effects is prevailing in control models found in the state-of-the-art literature.
The new control allocation technique explained further along in this paper proposes precisely to perform the inversion of (11) and (13),by means of a function fitting neural network that models,to take into consideration the aerodynamic forces that influence the quadcopter behavior and therefore command the correct angular velocities to the actuators.
Additionally,expanding (13),we obtain the following:
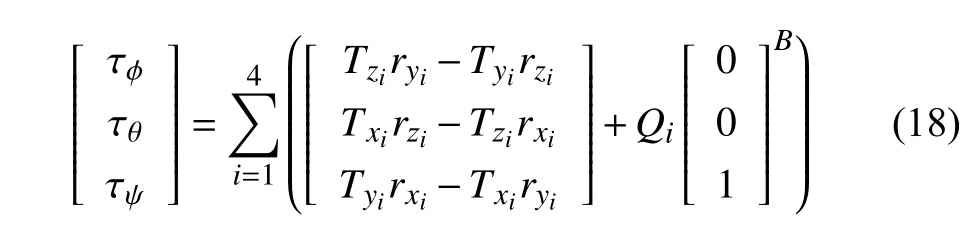
which gives us,for each actuatori,

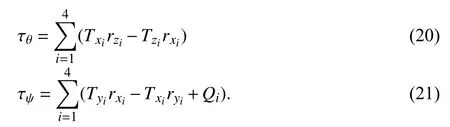
In (19)–(21),we make explicit the influence of the thrust components onxandy-axes on the torques that perform the roll,pitch,and yaw movements,τφ,τθ,and τψ,respectively.These components are neglected when using the traditional MMCA,which considers that the thrust only has thez-axis component.We state once more that,due to aerodynamic effects such as blade flapping,however,thrust and moments are not necessarily orthogonal to the body axis [19],so thesex-axis andy-axis components do exist.In Section V,we show that these componentsTxandTyare not of negligible order when compared to the order of the system torques they have an influence on.
D.Quadrotor Control Strategy
The block diagram for the position and attitude control system is shown in Fig.4.It is composed of an external PD trajectory control loop and an internal PID loop that controls the attitude which must be achieved so that the desired path is followed.Altitude or height control is also made through a PID controller.
TheTrajectory Generatorblock sends the path commands(x,y)to thePosition Controller.This controller outputs theroll(φ) andpitch(θ) commands to theAttitude Controller.The altitude (z) command comes directly from theTrajectory Generator,and theyaw(ψ) controller is independent.The respective adjustments in the angular velocities of the motors to achieve the desired behavior in φ,θ,ψ andzwill then be sent to the quadcopter through theControl Allocation.The sensing system must be adequate for good state feedback and,thereafter,an accurate calculation of the error.
We have the following expressions for the attitude PID controller,whereeφandeθrepresent the roll and pitch errors,respectively;Pis the angular velocity around thex-axis in the body-frame,andQis the angular velocity around they-axis in the body-frame:
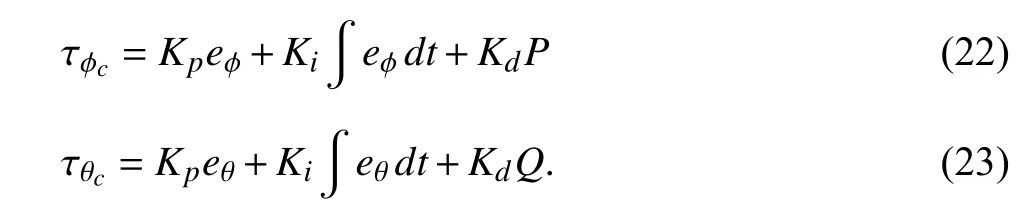
As aforementioned,the attitude controller commands are generated by the PD trajectory controller,shown in (24) and(25).Note that we need to perform a rotation around thez-axis(ψ) during the error calculation,because the body and inertial frames are not necessarily aligned in the same direction.
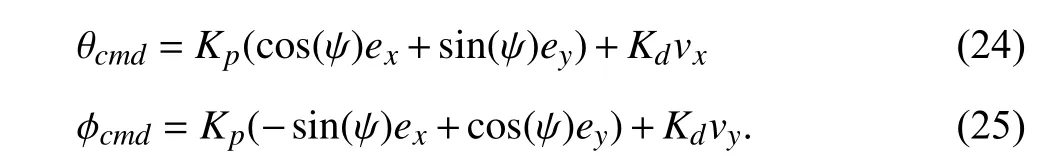
The yaw control is made separately,as in (26),whereeψrepresents the yaw error andRis the angular velocity around thez-axis in the body-frame
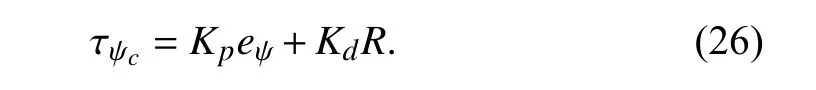

Fig.4.Block diagram for the quadrotor control strategy.
Finally,the height control is performed through a PID,as shown below:
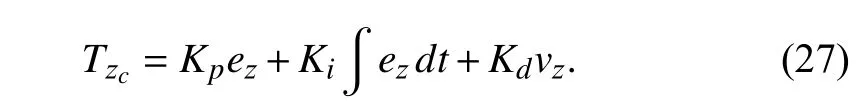
Since we aim to compare two different control allocation methods in this paper,the following assumption is naturally required.
Assumption 2:For the same controller design,simply replacing the traditional mixing matrix control allocation with the neural network control allocation here proposed does not harm the control project.
In order to verify this assumption,we designed a simple controller for the quadrotor system with the mixing matrix and tested to see if the project criteria were maintained when replacing it with the novel neural network control allocation we propose further ahead in this paper.
We set the project criteria of 1 s rising time (tr),which is the time when the output first reaches the reference,and 3 s settling time (ts),defined as the time when the output is within a 1% error when compared to the steady state.With this,we specified the corresponding proportional (Kp),integral (Ki) and derivative (Kd) attitude controller gains,shown in Table IV.
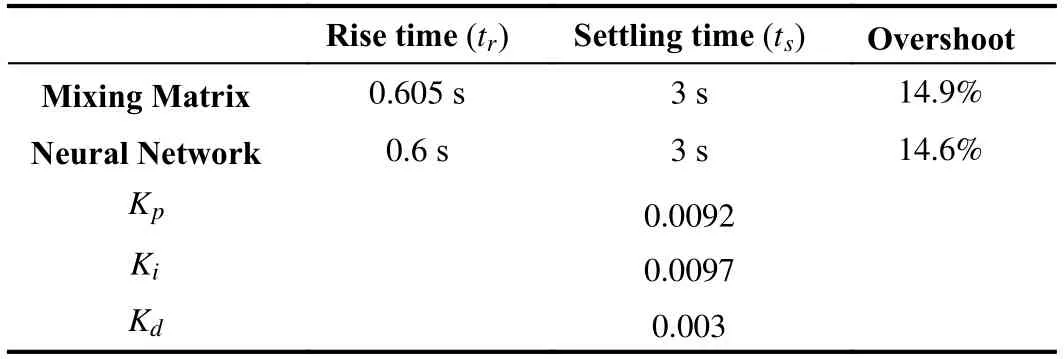
TABLE IVSTEP RESPONSE CHARACTERISTICS
The controllers were implemented in discrete-time,with the Bogacki-Shampine method,which is a requirement for it to be deployed to the hardware for real robot experiments afterwards.The step size was of 5 ms,which was chosen to match the sampling time of the quadrotor during flight experiments.Other parameters necessary for the simulation,such as constants that model the aircraft,were obtained from the documentation provided by the manufacturer.
The obtained step response behaviors are presented in Fig.5 and detailed in Table IV,for the traditional mixing matrix control allocation and the novel neural network control allocation.We can infer,comparing both step responses,that Assumption 2 is in fact true,as the difference between them is negligible.Therefore,it is possible to use the new control allocation approach and apply it to more elaborate maneuvers to observe the results.The PD-PID controllers were used here merely as a tool to perform the experiments and simulations,and are not the focus of the contributions of this paper.
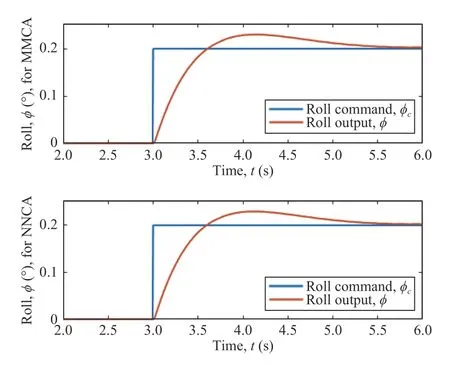
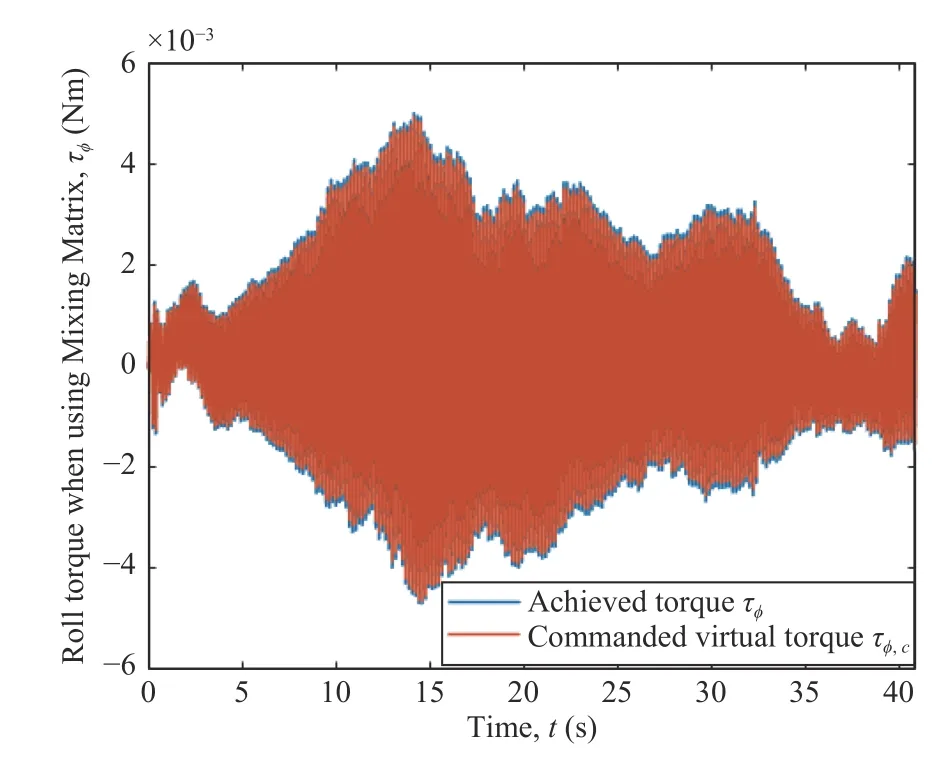
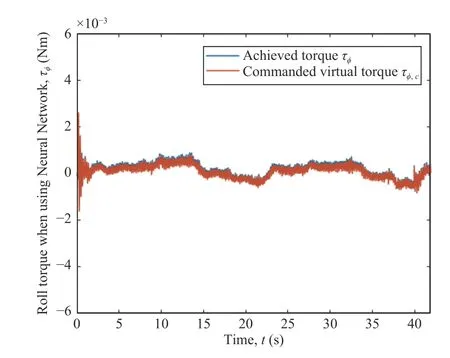
Fig.5.Roll step responses for the control system using the traditional mixing matrix (MMCA),on the top,and the proposed network control allocation (NNCA),on the bottom.
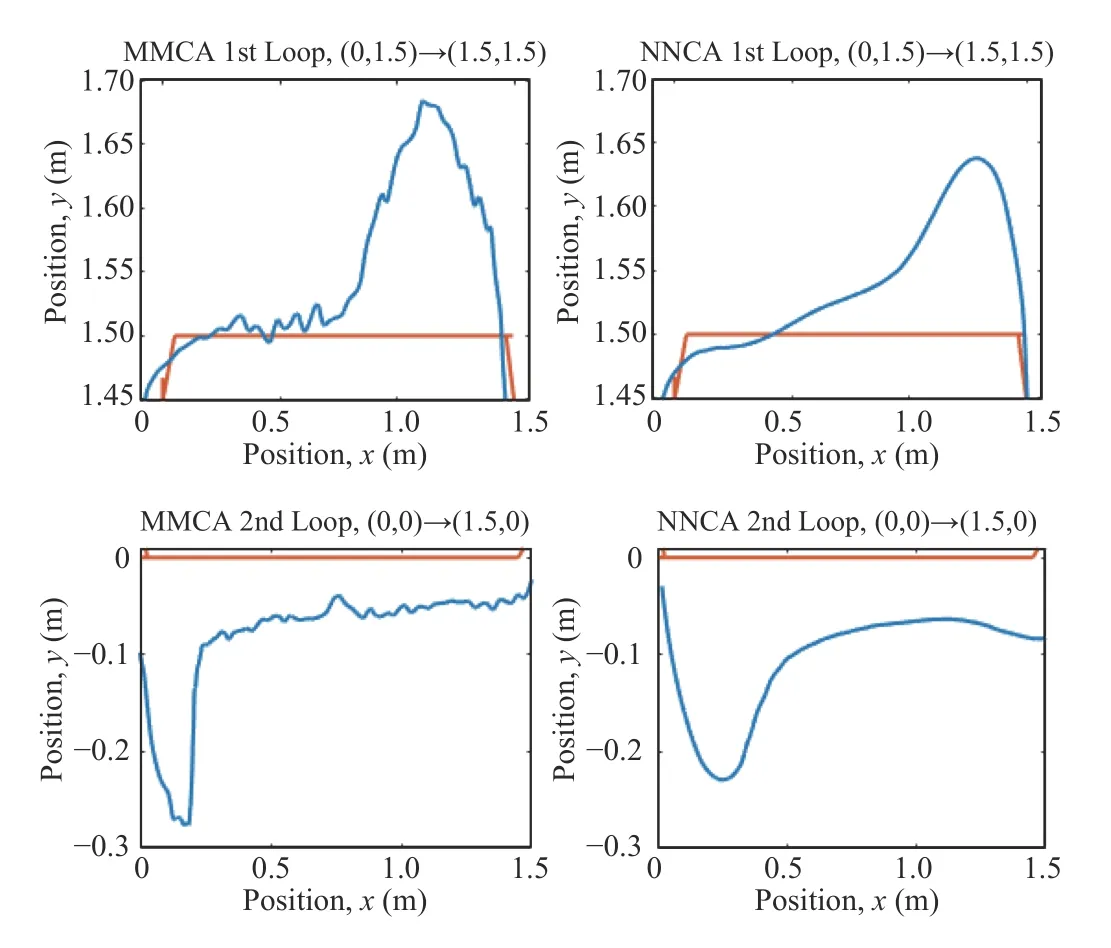
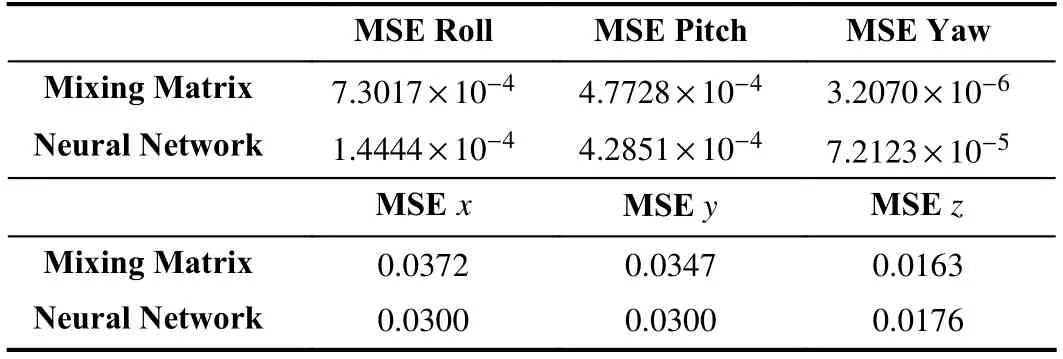
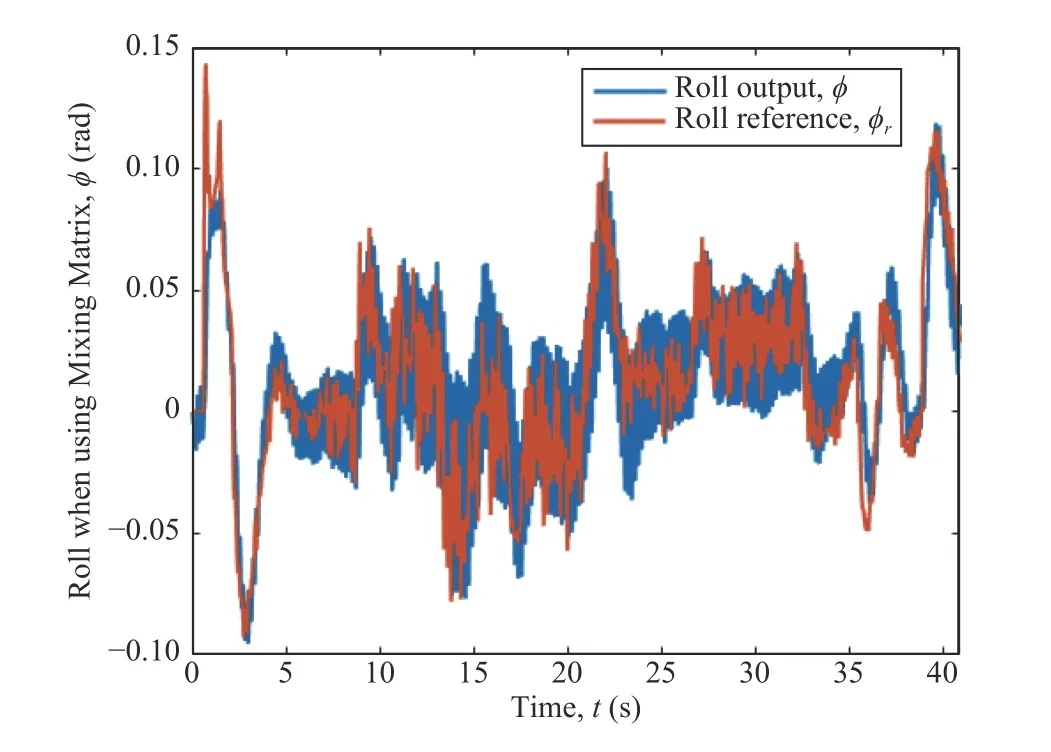
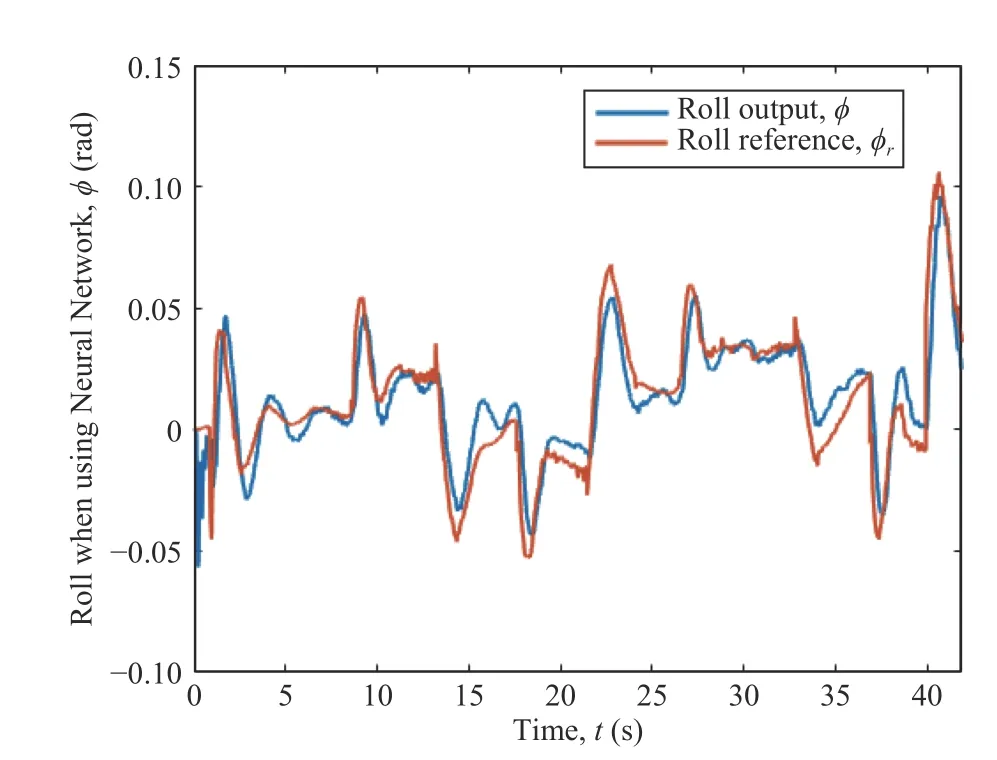
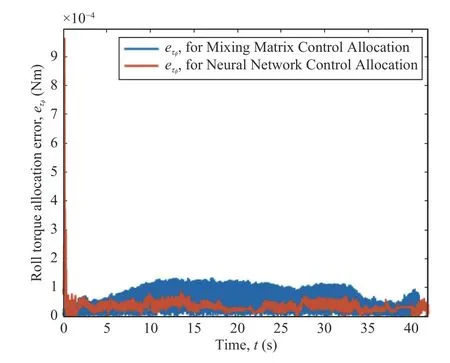
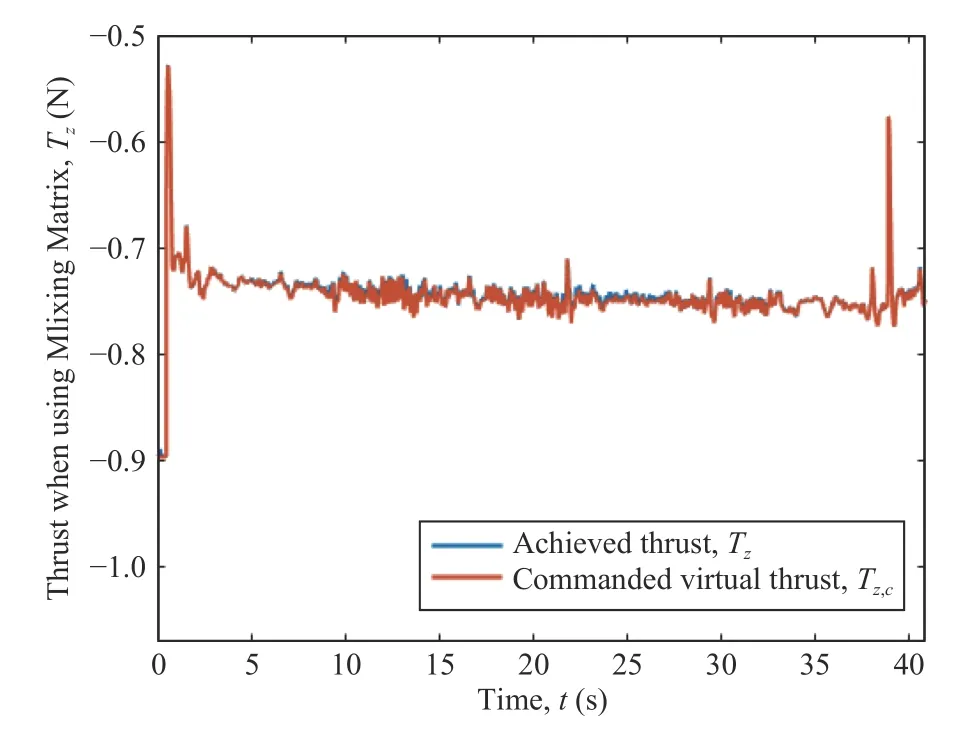
IV.NEURAL NETWORK CONTROL ALLOCATION
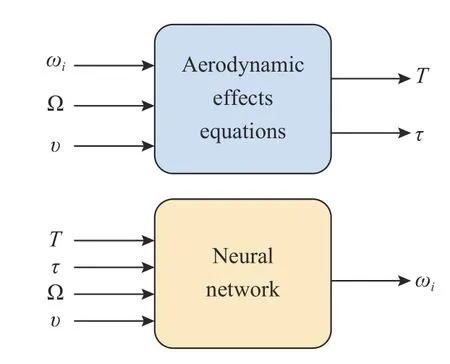
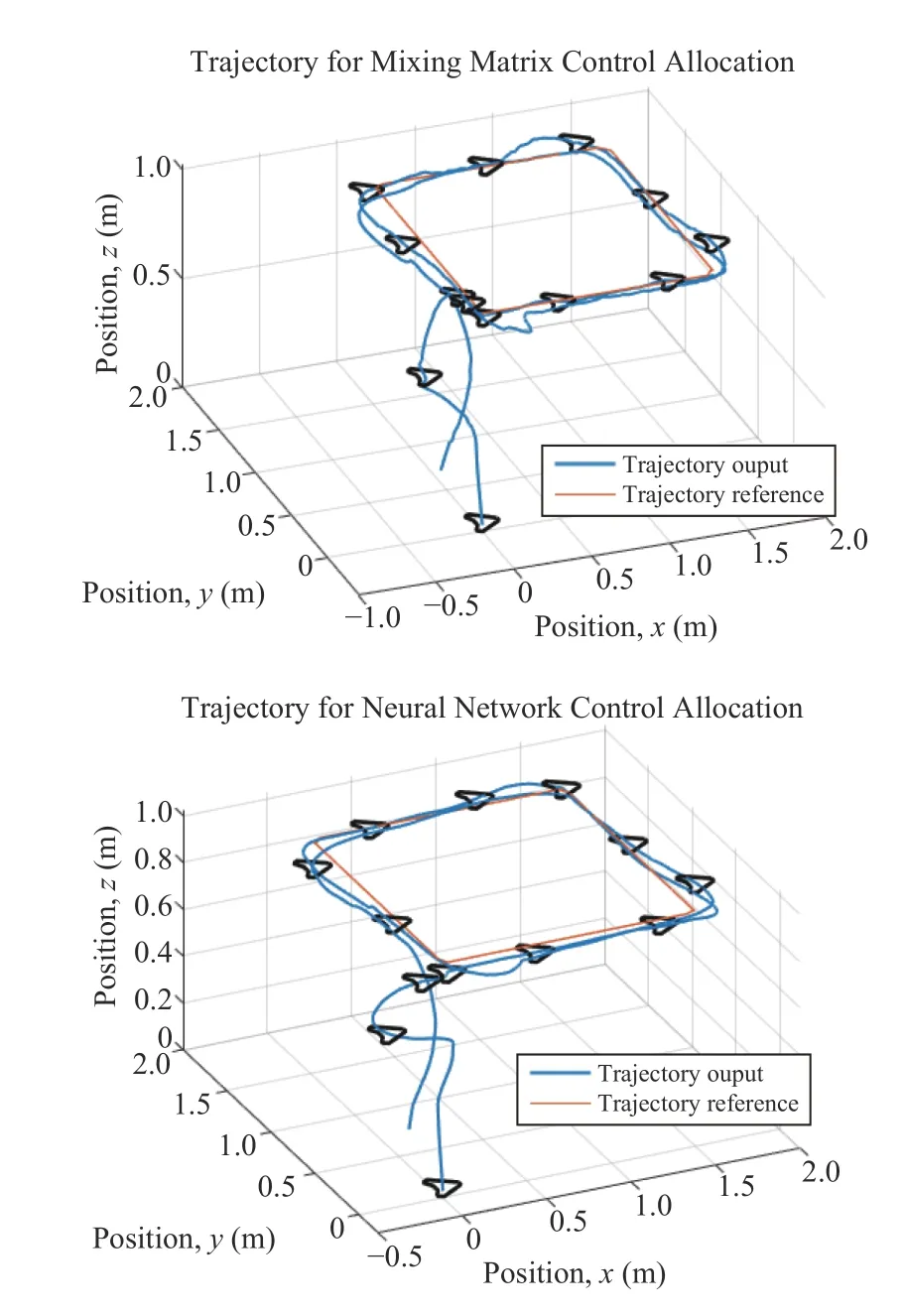
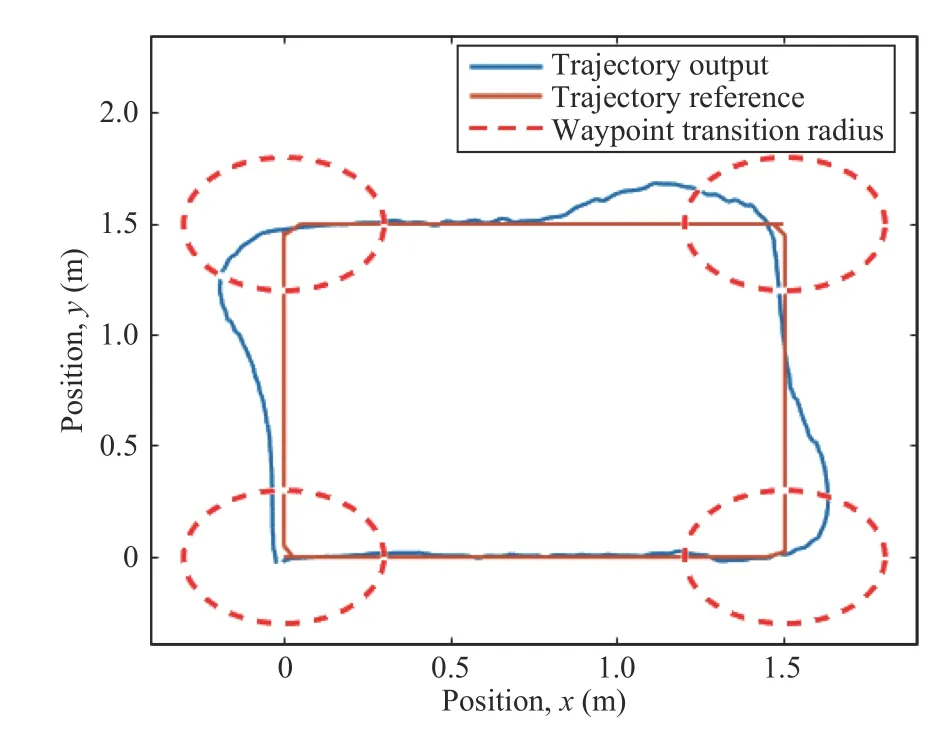
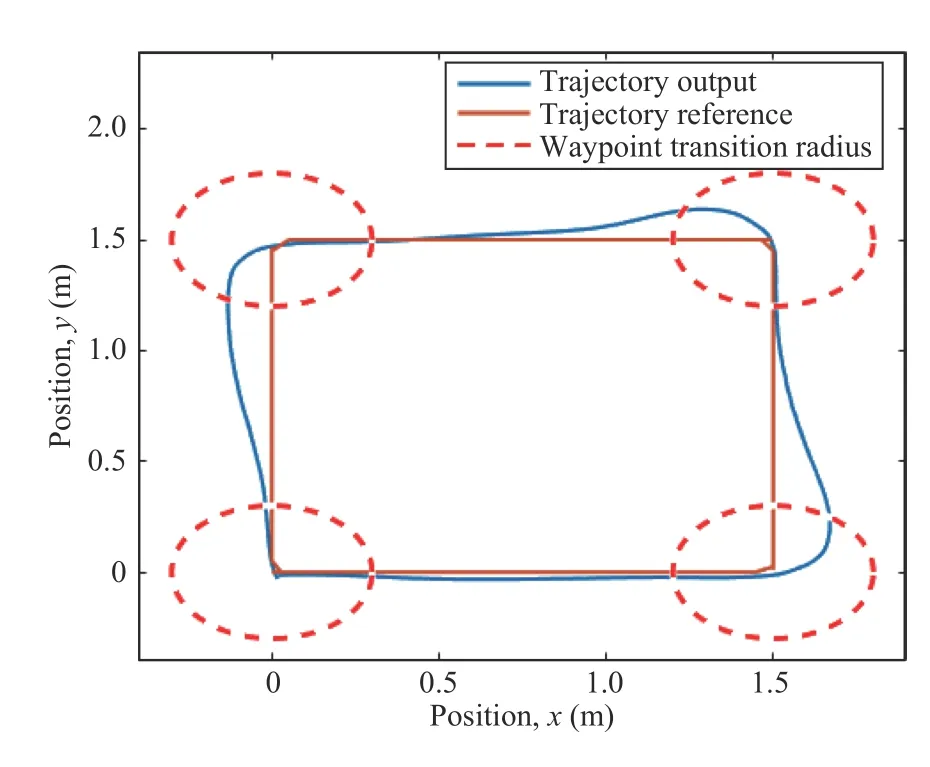
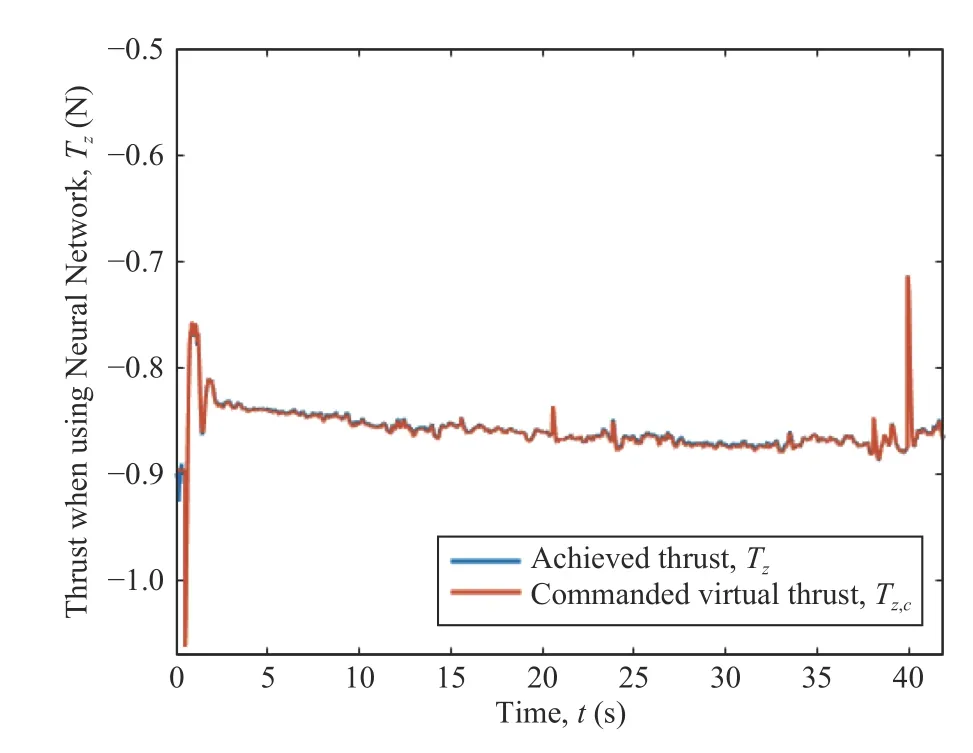
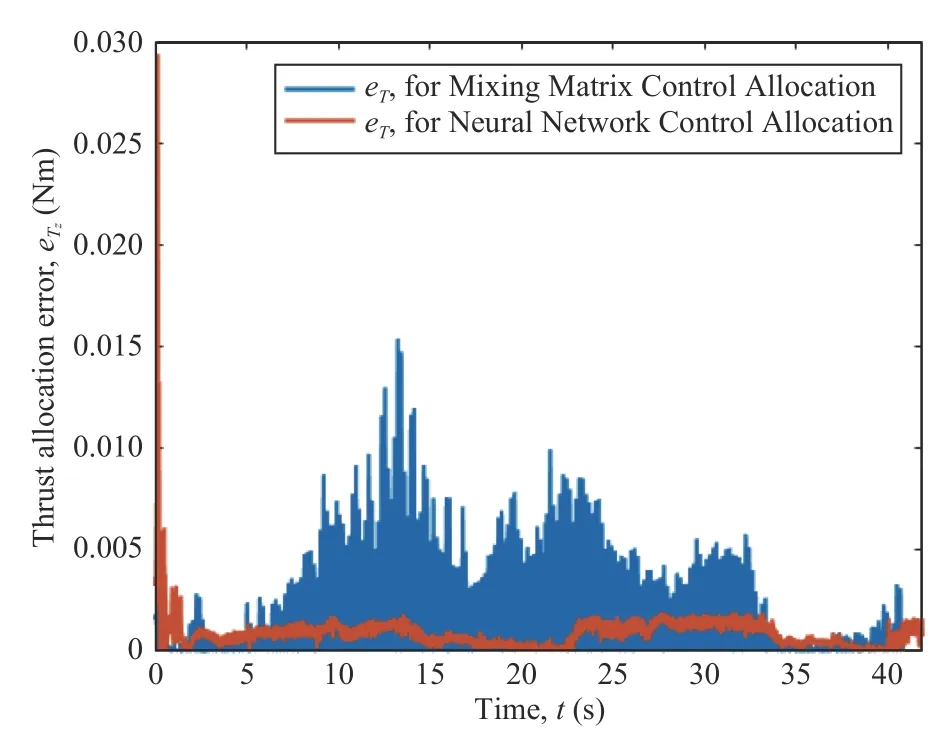
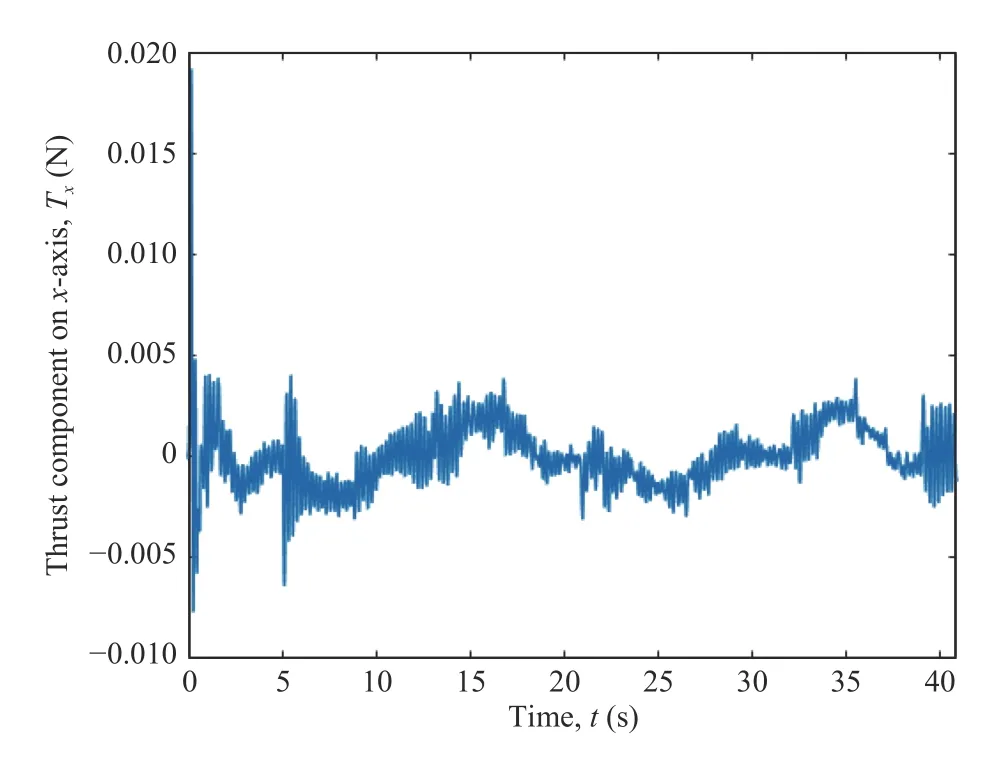
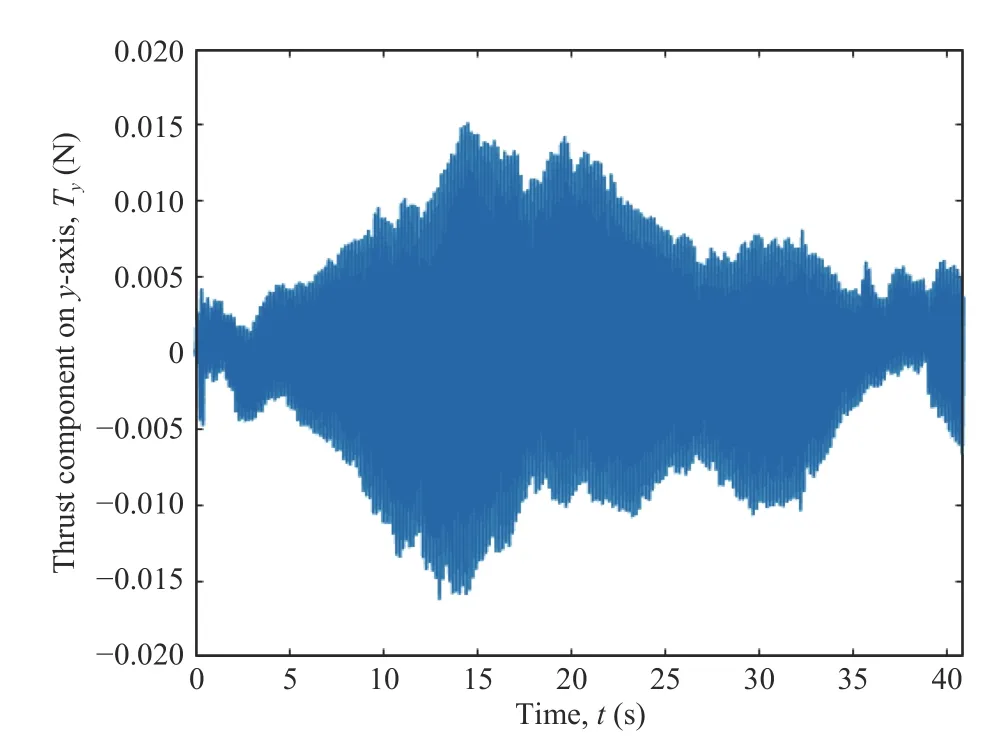
Generally speaking,a control allocation solves an undetermined,typically constrained,system of equations [29].The input to the control allocation block is the total control effect to be produced,or the virtual control input τc(t)∈Rk.Its output,on the other hand,is the achieved actuator commandu(t)∈Rm,wherem>kif the system is over-actuated,orm whereg:Rm→Rkis the mapping from the achieved actuator commands to the virtual control inputs in the system to be controlled [6].In the control allocation literature,(28) usually becomes withBbeing called the control effectiveness matrix of dimensionsk×mand rankk.Fig.6 illustrates the control allocation process.It must transform the virtual inputs τcinto commandsusent to the actuators such that they generate the allocated inputs τ=τc. Fig.6.Control system structure including control allocation.The motion control specifies a virtual control effort τc that must be produced,based on the reference signal r and the state feedback x.The control allocation distributes this control demand among the actuators,which generate the actual allocated control effort τ.If the allocation is successful,then τ c=τ. It is important to stress that,when it comes to the process of control allocation,the terminology used depends on the application in mind,so the control allocator can also be known as control mixer,control blender,control selector,or control distributor [6].Therefore,the control effectiveness matrix can be referenced by several notations.In quadcopter applications,it is usually called mixing matrix,referencing the control mixer;the control inputs are the thrusts and torques,and the actuator commands are the angular velocities ωifor each rotor. The traditional formulation of the linear control allocation problem is the system (30),which consists of (28) with the application of the actuator constraints [5],[6]. There are three possible outcomes when solving (30): 1) There is an infinite number of solutions; 2) There is one unique solution; 3) No solution exists. Many proposed control allocation methods correspond to different ways of computing the solution for a certain allocation objective,which most of the times is to avoid actuator saturation,rather than different objectives.The majority of well-established control allocation algorithms depend on numerical optimization to solve the control allocation problem.In this work,we briefly mention and describe the principal allocation methods according to Härkegård [6]. Optimization-based control allocation methods rely on a pragmatic interpretation of the control allocation problem,which states:for the system (30),determine a feasible control input so that this system is satisfied.If there are several solutions,pick the optimal one.In direct control allocation,the choice of control input is made unique by geometric reasoning.In daisy chain control allocation,the allocation suite is divided into groups,which are successively employed to generate the total control effort.All of these alternatives can be solved using numerical algorithms. The main problem approached when using control allocation in the literature is the saturation of actuators in over-actuated systems.The principles of control allocation are however general and can be used to optimize other disturbances in the systems,from power or fuel consumption to aerodynamic effects [5],which is the case of this paper. The problem of allocating the proper angular velocities to the rotors,which will generate the commanded virtual thrust and torques,is solved with an analytical inversion of (11) and(13),which transforms the angular velocities into thrust and torques,ωi→[T,τ]. We need therefore a solution to perform the opposite operation,(as described in Section III-A),from the virtual control inputs to the rotor velocities,[Tc,τc]→ωi,considering the aerodynamic effects introduced in Section III.This inverse transformation would derail the invertible relation of the classic mixing matrix and hinder its usage.In this work,we propose the use of a neural network to perform the function fitting for finding,and use it as the control allocation. Definition 5 (Neural Network Control Allocation (NNCA)):The control allocation performed by means of a function fitting neural network that provides a transformationof the plant inputto the actuator commandstaking into account aerodynamic effects as described in (11) and (13). That is,as in Section III-A, Function fitting is the process of training a neural network on a set of inputs with the aim of producing an associated set of target outputs.After the network has been created with the desired hidden layers and the training algorithm,the neural network must be trained using a set of training data.Once the neural network has fitted the data,it forms a generalization of the input-output relationship.The trained network can therefore be used to generate outputs for a new set of inputs that was not used in training.Neural networks are good at fitting functions.There is proof that a fairly simple neural network can fit any practical function [45],[46]. The proposed function fitting neural network is composed of a two-layer feed-forward network with sigmoid hidden neurons and linear output neurons.This structure was chosen since it can fit multi-dimensional mapping problems arbitrarily well,provided consistent data and enough neurons in its hidden layer are given.In this case,20 neurons were used for the first step of the training,and 10 neurons for the second one,as described below. The neural network control allocation approach has a twostep training process in order to take into account the aerodynamic effects,as well as achieving desirable training performance and mean squared error (MSE) order.The second step of the training process is independent from the mixing matrix. In the mathematical model presented in Section III-C,we do not represent uncertainties caused by nonlinear terms.Nonetheless,the curve fitting provided by the neural network imposes an approximation error influenced by uncertain nonlinear terms. With the purpose of minimizing the effect of these uncertainties,we aimed for a certain MSE order based on recent works in the literature regarding curve-fitting using neural networks [47]–[49].To achieve this goal,we used our two-step training process,as will be described next.Thereferences found in literature used radial basis function (RBF)networks for the curve-fitting.Considering that,we first trained RBF neural networks using the same mentioned twostep training method.Our objective was to compare the MSE of these RBF results to the MSE of the network structure we are using and see if they agree with the results found in the literature [47]–[49].The complete neural network training is described next and summarized in Table V. TABLE VMSE FOR THE NEURAL NETWORK TRAINING PROCESS For the RBF networks,the training process was the same as below,with the exception of the training algorithm,which was performed using the MATLAB functionnewrbe().In the first training,the RBF network obtained an MSE of 4.2×10−2.In the second training,the RBF network achieved an MSE of 6.0297×10−4.These error orders are expected,according to the literature [47]–[49].If we compare these results with the ones of our proposed network,detailed in Table V,it is possible to conclude that not only are they within the expected MSE order of previous works,but our results are slightly better than the MSE obtained with the RBF networks and the same training data. ● First Training 1) An open-loop simulation of the quadrotor system without any controller was performed,using pseudo-random binary sequence (PRBS) pulses with amplitude 0.2 as mechanical conjugates (Tc,τc) to collect the corresponding angular velocities outputs (ωi) .Other variables (v and Ω) were also collected for training,as detailed in Fig.7. Fig.7.Block diagrams representing the variables used for neural network training and therefore for neural network control allocation. 2) The collected angular velocities data were applied to the aerodynamic effects equations (11) and (13) aiming to collect the real mechanical conjugates (T,τ) established at the aircraft. 3) The input-output data (T,τ,Ω,v →ω1,ω2,ω3,ω4) were then used for the first training step,using the Bayesianregularization algorithm. With the first training,we obtained a mean squared error of the order 1 0−2,as detailed in Table V.To refine the network and obtain an MSE order of at least 1 0−3as in the mentioned recent works found in the literature [47]–[49],the second training was performed,using the results of the first one. ● Second Training 1) A new set of input-output data were collected from a closed-loop simulation with the first trained network as the control allocation method and a PD-PID error controller. 2) 3-2-1-1 maneuvers were used as attitude commands,and the network obtained in the first step converted the virtual control commands (Tc,τc) into angular velocities (ωi). 3) Once more,the collected angular velocities data were applied to the aerodynamic effects equations (11) and (13)aiming to collect the real mechanical conjugates (T,τ)established at the aircraft. 4) The input-output data (T,τ,Ω,v →ω1,ω2,ω3,ω4) were then used for the second neural network training,performed using the Levenberg-Marquadt algorithm.This time,we obtained the MSE of the order 1 0−4. Both training steps were carried out for a maximum of 1 000 epochs or until the validation error failed to decrease for 6 iterations,and we obtained Regression values ofR=0.99999 for the two steps.Regression values measure the correlation between outputs and targets.AnRvalue near 1 means that the variables are strongly related,while anRvalue near 0 means that they have little to no impact on each other. The whole training process was performed offline,meaning that during the flight this allocation method requires low computational power,because the network is already trained and no update is made on-line.The classic mixing matrix was only used in the first step of the training to collect data. While the mixing matrix control allocation uses only the thrust and torques to perform the matrix inversion and obtain the squared angular velocities,more variables were added to the neural network training process for the purpose of obtaining a better fit,according to the aerodynamic effects modeled in Section III-C.See Fig.7,which details the input and output variables used in training.Therefore we used 10 input elements (Tz,τφ,τθ,τψ,Ωφ,Ωθ,Ωψ,vx,vy,vz),withTzas thez-axis component of the trustT,which comes from the height controller,to obtain 4 output elements (ω1,ω2,ω3,ω4).During the UAV flight,these additional state variables (v and Ω) are obtained from sensing. The platform used in the flight experiments was a PARROT Mambo minidrone,illustrated in Fig.1,which contains a downward-facing camera for positioning using optical-flow odometry,an ultrasonic sensor,a barometric sensor,and an inertial measurement unit (IMU).All these sensors are used for stabilization purposes.The minidrone dimensions are 180 mm × 1 80 mm × 4 0 mm,with a weight of 7 0 g.Power is provided by a 3 .7 V,5 50 mAh,2 Wh Li-Po battery,enabling a flight time of 7–10 minutes,depending on the nature of the task to be performed and the accessories implemented.The applied control strategy for the quadcopter operation consisted of the PD-PID controller mentioned in Section III-D,again implemented in discrete-time,with the Bogacki-Shampine method and a step size of 5 ms.In Fig.4,theactuators(rotors)andquadrotor dynamicsblocks represent the minidrone,while the other blocks correspond to the algorithm embedded in the aircraft. We evaluated the proposed method by comparing the mechanical conjugates at the output of the controller (the virtual control commandsTc,τc) to those established at the aircraft (T,τ),which were calculated using the inflow and blade flapping equations.We also analyzed changes in the controller performance.The neural network was able to closely matchT,τ andTc,τc,while the classic control allocation with the mixing matrix could not achieve the same performance.The error between the two mechanical conjugates (τ −τcandT−Tc),called allocation error,was also determined in both cases.We were able to enhance the performance of the PD-PID controller with the new control allocation,without altering the controller gains,that is,the tuning was the same for both the traditional mixing matrix and our proposed neural network control allocations. Our position reference consisted of a set of waypoints for the quadrotor to follow.They formed a square with a 1 .5 m side and a transition radius of 0.3 m to maneuver through the corners,as well as take-off and landing commands.The experiment consisted of the minidrone taking-off in the bottom-left corner of the square.Then the UAV performs a pitch forward movement until it reaches the next corner,then a roll lateral movement,a pitch backward movement,and then again a roll lateral movement.This path is repeated once more,and then the minidrone lands,resulting in a total of 9 waypoints [0 0 1;1.5 0 1;1.5 1.5 1;0 1.5 1;0 0 1;1.5 0 1;1.5 1.5 1;0 1.5 1;0 0–1].Here thez-axis value 1 represents the height (1 m) at which the drone navigates along the square path.Fig.8 shows the trajectory reference and output for the complete path of the waypoint following,with take-off and landing,highlighting the aircraft positioning in black,for clarity’s sake.The yaw orientation reference of the quadrotor was fixed throughout the experiment. Fig.8.Trajectory reference and output for both loops of the waypoint following,with take-off and landing,highlighting the aircraft positioning,for the sake of clarity. The test scenario was planned for a minidrone,which is a type of aircraft especially susceptible to aerodynamic effects influence,as aforementioned.The path was designed to induce mildly abrupt roll and pitch maneuvers (the corners of the square,that is,the waypoints) that would also allow an adequate observation of said effects.The behavior of the quadrotor throughout the trajectory however was not intended to be aggressive as mentioned in previous works in the literature,because we wanted to highlight the importance of the consideration of aerodynamic effects in the control allocation even without aggressive maneuvers.Note the trajectory used in this experiment differs from the maneuvers used for the neural network training explained in Section IV-A,hence the training does not need to be repeated for each specific maneuver.Furthermore,Table III shows some constants relative to the quadcopter in use,which were obtained from the documentation made available by the manufacturer.These constants are used in the aerodynamic effects modeling in Table II. Fig.8 shows the three-dimensional representation of the commanded and followed trajectory,with take-off and landing,for the mixing matrix and neural network control allocations.Figs.9 and 10 show the trajectory projection in thexy-plane of the first loop for the same respective cases.We omit the aircraft’s second loop through the square in Figs.9 and 10 to facilitate visualization.We set atransition radiusas 0.3 m,shown as the red circle in the figures.It means that when the drone is approaching a waypoint,this value is used as the radius around the waypoint where the drone starts moving towards the next point.If the transition radius is set as 0.3 m,and the drone is 0.3 m away from the waypoint,the drone starts moving towards the next waypoint.The accuracy of reaching a specified waypoint increases with a decrease in the value of transition radius.Notice that the path following is more smoothly achieved with the neural network control allocation approach,while with the mixing matrix some stuttering is present when pursuing the commanded trajectory.This is emphasized in Fig.11,where some parts of the trajectory are highlighted to show the difference in path following for the mixing matrix and neural network control allocations. Fig.9.Projection (x,y) of trajectory reference and output when using the mixing matrix control allocation. Fig.10.Projection (x,y) of trajectory reference and output when using the neural network control allocation. The respective mean squared error (MSE) calculations for each axis are shown in Table VI,for angular and linear positions.For every case except the yaw angle and positionz,the MSE is smaller when using the neural network,especially in the case of the roll angle,where we had the most improvement when using the new control allocation. The performance of the UAV during the roll angle maneuver can be seen in Fig.12,for the mixing matrix,and in Fig.13,for the neural network control allocation.The mixing matrix approach shows a much noisier behavior and a higher amplitude variation when compared to the neural network control allocation approach,where the adherence of the output to the commands is much more reliable,stable,and therefore preferable for the quadcopter flight.The difference between the reference signals in both cases is due to the consideration of the aerodynamic effects in the control allocation algorithm. Fig.11.Augmented parts of the trajectory to show the difference in path following behavior for the mixing matrix (MMCA) and neural network(NNCA) control allocations. TABLE VIMEAN SQUARED ERRORS FOR THE ANGULAR AND LINEAR POSITIONS FOR BOTH MIxING MATRIx AND NEURAL NETWORK CONTROL ALLOCATIONS Fig.12.Roll commands and output when using the mixing matrix control allocation. Figs.14 and 15 show the comparison between the commanded virtual roll torques,which are commanded at the output of the controller.These figures also show the achieved roll torques at the aircraft,which were calculated using (13)with experimental flight data.Fig.14 refers to the experiment with the mixing matrix,while Fig.15 uses the neural network control allocation.The amplitude of the roll torques when using the neural network is smaller,requiring less effort from the quadrotor.Also,a comparison between the allocation errors for both cases is shown in Fig.16,proving that the neural network allocation considering aerodynamic effects significantly reduces the allocation error. Fig.13.Roll commands and output when using the neural network control allocation. Fig.14.Comparison between commanded roll torques at the control output and those achieved at the plant for the mixing matrix control allocation. Likewise,Figs.17 and 18 present the corresponding comparison for commanded virtual thrusts and achieved thrusts,for mixing matrix and neural network control allocations,respectively.We note a similar behavior as the roll torque case mentioned above.There are less noisy oscillations when using the neural network,as well as smaller amplitudes.Fig.19 shows the allocation errors for the two methods,where the error when applying the neural network control allocation is several times smaller (in the order of 10−1) than the traditional alternative with the mixing matrix. Finally,Figs.20 and 21 show the thrust TBcomponents on thexandyaxes,TxandTy,during the quadrotor flight when using the mixing matrix,which considers these components to be zero or negligible.Not only these components do exist,but they are not of negligible order when compared to the order of the system torques they have an influence on.For instance,Fig.21 showsTywhich has influence on the roll torque,as in(19).Note that the behavior of the roll torques seen in Fig.14 greatly resembles that ofTyin Fig.21. Fig.15.Comparison between commanded roll torques at the control output and those achieved at the plant for the neural network control allocation. Fig.16.Comparison between the allocation errors for the achieved roll torques (τφ) at the plant for both the mixing matrix (in blue) and neural network (in red) control allocations. Fig.17.Comparison between the commanded thrust at the control output and that achieved at the plant for the mixing matrix control allocation. Fig.18.Comparison between the commanded thrust at the control output and that achieved at the plant for the neural network control allocation. Fig.19.Comparison between the allocation errors for thrusts,in the z-axis(Tz),achieved at the plant for both the mixing matrix (in blue) and neural network (in red) control allocations. Measures were also taken during the flight experiments to minimize the error due to nonlinear uncertainties,since they were performed in a controlled indoors environment.The uncertain nonlinear terms were not directly treated in the modeling presented in this paper,as it was not the focus of this work.However,the practical results discussed here already show the advantages of the proposed method.In a future work,an approach considering these uncertainties could be included. In this paper,we demonstrated that the disregard of aerodynamic effects in the quadrotor control intending to simplify the process of converting the conjugates at the controller output to angular velocities to be commanded to the rotors greatly affected the flight performance,most specifically thrust and torque behaviors.We proposed that the aerodynamic effects could be taken into account by applying a more refined control allocation process that used a function fitting neural network to transform virtual control inputs into actuator commands.The control algorithm,which was a PDPID controller,did not need to acknowledge the aerodynamic equations directly. Fig.20.Thrust component in the x-axis,Tx,when using the mixing matrix control allocation. Fig.21.Thrust component in the y-axis,Ty,when using the mixing matrix control allocation. The network training was performed offline,requiring very low computational power when compared to other optimization-based control allocation algorithms.The neural network required a two-step training process that was independent of the classic simplified allocation method on its second step.The first training was performed in an open-loop system,via PRBS pulses.A second training was executed with the purpose of refining the network in an equivalent closed-loop system,and in this case,the allocation was implemented using the open-loop trained neural network alongside the PD-PID error controller. The experimental flight results showed that the aircraft behavior was smoother when using the neural network control allocation approach,the allocation error was smaller and the signals were less noisy,that is,the consideration of aerodynamic effects into the system interfered directly and positively with the quadrotor performance.Finally,the performance of the controller also improved with the use of the neural network control allocation,as well as the quality of the thrust and torque signals. The focus of this paper was the control allocation technique,not the controller project itself,which will be the focus of future works that will consider the aerodynamic effects in a nonlinear dynamic inversion controller using neural networks. APPENDIx THRUST ROTATION Note that,with this development,we can actually rewrite(12),shown in [10],using (35),as a function of the rotation of the flapping angles,as in (32) shown in Proposition 3. Lemma 1:The longitudinal and lateral flapping anglesa1,s,iandb1,s,iare Proof:Now,analyzing the other terms on Table II,let us start with the sideslip rotation matrix Jss,i.It can be interpreted as the rotation ofji,defined in Table II and in Fig.22,along thezaxis,as in (38) below: Fig.22.v ra,i projection on the x y-plane. It is important to remember that (39) and (40) are equivalent because the inverse of a rotation matrix is equal to its transpose.Therefore,we can rewrite the longitudinal flapping βl f,i,also on Table II,as ACKNOWLEDGMENT The authors thank PPgEE,DEE-UFCG,CAPES and CNPq for the award of research grants and study fellowship during these investigations

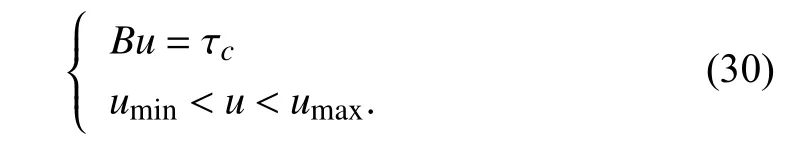
A.Neural Network Design


V.RESULTS
VI.CONCLUSIONS

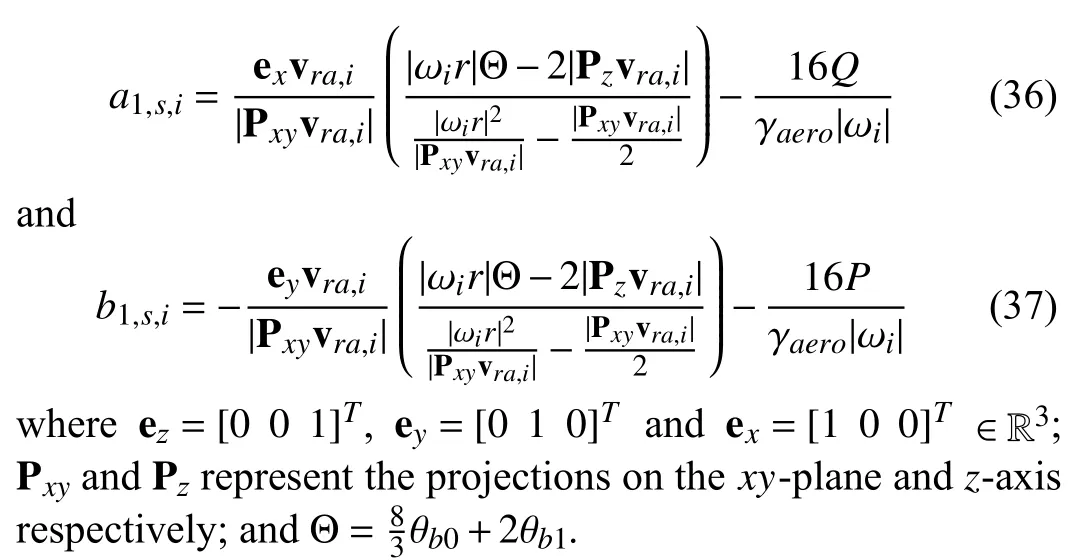

杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Sampling Methods for Efficient Training of Graph Convolutional Networks:A Survey
- Fault Accommodation for a Class of Nonlinear Uncertain Systems With Event-Triggered Input
- Precise Agriculture:Effective Deep Learning Strategies to Detect Pest Insects
- Maximizing Convergence Speed for Second Order Consensus in Leaderless Multi-Agent Systems
- Exponential Set-Point Stabilization of Underactuated Vehicles Moving in Three-Dimensional Space
- An Adaptive Rapidly-Exploring Random Tree
