小应变亚塑性黏土本构模型在PLAXIS中的实现及应用

司海宝，徐 辉，毕庆龙

(1.安徽工业大学建筑工程学院，安徽 马鞍山 243032；2.皖西学院建筑与土木工程学院，安徽 六安 237005)

亚塑性理论是基于连续介质力学、运用张量工具研究土体中某点应力与应变率之间的函数关系，具有严格的数学推导过程[1]。小应变亚塑性黏土本构模型将临界状态土力学、小应变理论嵌入到亚塑性土体本构方程中，是研究静载荷、动载荷作用下土体非线性特征的重要数值计算方法。该模型克服了传统弹塑性力学中人为划分土体弹性变形与塑性变形的困难，能够描述土体硬化与软化过程，目前在工程中得到广泛应用[3]。德国学者Kolymbas[4]率先采用单一非线性张量分析材料的非线性力学特征，由此亚塑性本构模型得到迅速发展；Wu等[5]针对砂土变形特性提出四参数亚塑性本构模型；VonWollffersdorff[6]在四参数亚塑性本构模型基础上，提出考虑土体孔隙率的八参数亚塑性砂土模型；岑威钧等[7]在土体线性变形项中添加体应变控制变量，编写出基于ABAQUS软件平台粗粒土材料子程序；明华军等[8]将颗粒破碎临界面方程嵌入到亚塑性模型中；刘国明等[9]和熊保林等[8]针对砂土的横观各向异性，提出改进的Wollffersdorff亚塑性本构方程。以上研究主要针对无黏性土体的应力变形分析。对于黏性土体，Mašín[11]和Fuentes等[12]将临界状态土力学理论嵌入到亚塑性本构方程中，用于分析土体在外载荷作用下的单调响应；之后Fuentes 等[13]把小应变引入到黏土亚塑性本构模型中，用于分析循环载荷作用下土体的应力应变关系。

利用现有商业软件强大的非线性计算能力和便利的前后处理能力开展二次开发是土体本构模型推广应用的有效途径。司海宝等[14-15]利用二次开发接口，编写邓肯-张、南水模型和状态相关砂土本构模型三维用户子程序；王明强等[16]利用二次开发接口，编写分级单屈服面用户子程序并验证子程序的稳定性。PLAXIS有限元软件是一套功能强大的仿真计算平台，具有较强的非线性处理能力。对于循环载荷分析，PLAXIS 有限元软件提供小应变硬化模型，但模型参数物理意义不明确，参数标定需进行非常规试验，工程应用困难[17]。鉴于此，利用用户自定义材料属性的二次开发接口，将小应变亚塑性黏土本构模型嵌入到PLAXIS有限元软件中，为分析循环载荷作用下土体的变形提供一种新的方法。

1 小应变亚塑性黏土本构模型参数

Mašín[11]将亚塑性理论引入土体本构方程之中，提出了黏性土体亚塑性本构模型，该模型保留了Von Wolffersdorff[6]对亚塑性理论的本质，其本构方程为：

式中：⊗表示张量叉积；ηδ=δ/‖δ‖；ρ= ‖δ‖/R；R为土体材料参数；I为应力单元张量；ρr为标量函数；ηδ和ρ分别为土体小应变张量的方向以及范数；mR为卸载时土体的初始剪切模量；mT为加载时土体的初始剪切模量，用模型参数mrat=mT/mR替代参数mT，张量函数L和N分别表示为：

式中：ησ和ϑ分别为应力率和罗德角；Ag和ng为材料参数。

至此小应变亚塑性黏性土体本构模型包含临界状态参数φc，N，λ*和k*；正常固结土体体积刚度与切向刚度比例系数Vpp；小应变参数R，βr，χ，mrat，Ag和ng。

2 小应变亚塑性黏土本构模型子程序

2.1 本构模型子程序的实现

小应变亚塑性黏土本构模型是针对黏性土体在外载荷作用下的应力应变响应，需确定土体的初始应力状态(两个重要的状态参数，即平均有效应力和初始孔隙比或超固结比)，采用自适应积分算法求解得到的本构模型方程为

式中：t为时间；y为本构方程中的应力(或应变)，采用龙格-库塔法求解，按傅里叶级数展开如下：

误差控制采用二阶和三阶差值，满足

式中k1，k2分别为时间段开始和时间段中点的斜率。

若在达到最小时间步长或规定的最大计算步长后仍不能满足上述误差控制，则要求拒绝当前步长、并减小全局时间步长重新迭代计算。根据上述推导，采用FORTRAN语言编写子程序，生成动态链接库DLL 文件，并置于PLAXIS 安装目录下，在PLAXIS 软件选择用户自定义模型，输入自定义的土体模型参数，实现小应变亚塑性黏土本构模型程序在PLAXIS 软件中的二次开发与调用，模型参数输入界面如图1。

图1 小应变亚塑性模型参数输入界面Fig.1 Parameter input interface of small strainhypoplastic model

2.2 本构模型子程序的验证

常规三轴试验能较好地反应土体在外载荷作用下受力变形的全过程。小应变黏土亚塑性模型参数主要分为两类：基本材料参数(φc，λ*，k*，N，Vpp)，主要通过固结试验和常规三轴试验来校准；小应变材料参数(Ag，ng，mrat，R，βr，χ)，通过循环三轴试验来标定。为验证文中二次开发的小应变亚塑性黏土本构模型子程序的合理性，采用开发的子程序分别对多特蒙德黏土常规三轴试验和高岭土循环三轴试验进行模拟分析，且与文献试验结果进行对比。

2.2.1 常规三轴试验模拟验证

多特蒙德黏土亚塑性模型计算参数见表1[18]。不同围压(190，290，390 kPa)下，多特蒙德原状黏土轴向应变及平均有效应力与偏应力关系的模拟与试验结果[18]分别如图2，3。

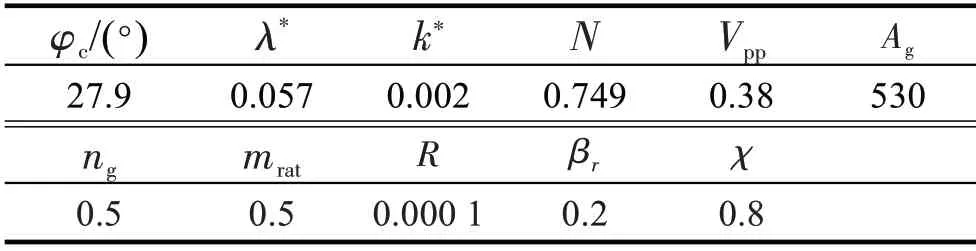
表1 多特蒙德黏土亚塑性模型材料参数Tab.1 Material parameters of Dortmund clay hypoplastic model

图2 多特蒙德原状黏土轴向应变与偏应力关系曲线Fig.2 Curves of relationship between axial strain and deviatoric stress of Dortmund clay

图2 表明：子程序模拟结果与试验结果一致性较好，随偏应力逐渐增大轴向变形逐渐增大，土体呈现硬化特征；低围压(190 kPa)时，模型过高地估计了剪切模量的退化速率，轴向应变模拟结果大于试验结果，但随偏应力继续增大，剪切模量的退化速率逐渐接近试验值；较高围压(390 kPa)时，剪切模量的退化速率与试验值一致性较高。由图3 可知：低围压(190 kPa)时，偏应力模拟结果小于试验结果，随偏应力继续增大偏应力模拟结果与试验结果基本吻合；高围压(390 kPa)时，模拟应力路径与试验基本一致。由此表明开发的亚塑性黏土本构模型子程序计算结果稳定可靠。

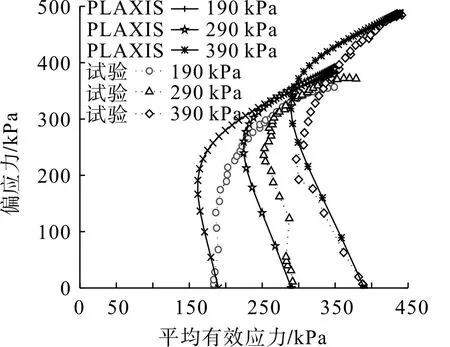
图3 多特蒙德原状黏土的平均有效应力与偏应力关系曲线Fig.3 Curves of relationship between average effective stress and deviatoric stress of Dortmund clay

2.2.2 循环三轴试验模拟验证

为进一步验证开发子程序的合理性，对高岭土循环三轴试验[12]进行模拟分析。高岭土小应变黏土亚塑性模型参数见表2[12]，初始固结压力p0=200 kPa、土样初始孔隙比e0= 1.0、动应力幅值qamp=70 kPa，模拟与试验结果见图4。

表2 高岭土亚塑性模型材料参数Tab.2 Material parameters of Gaolin clay hypoplastic model

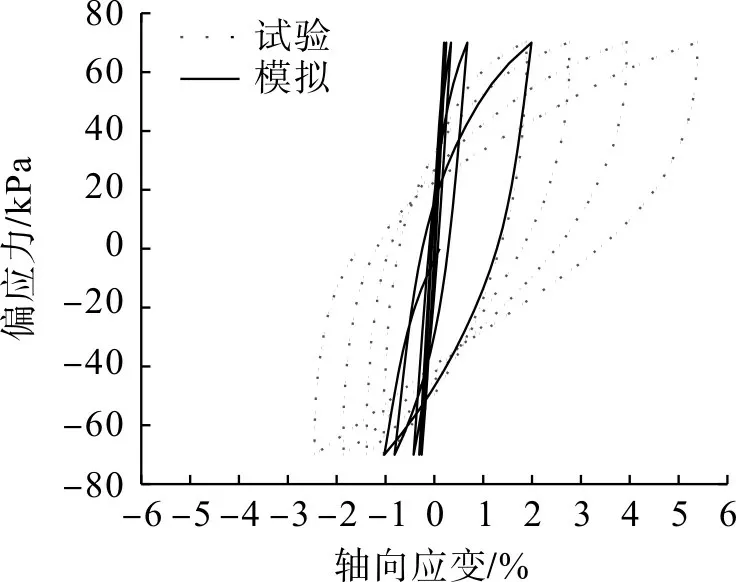
图4 高岭土轴向应变与偏应力关系曲线Fig.4 Curves of relationship between axial strain and deviatoric stress of Gaolin Clay

由图4可看出：前五循环周期，随载荷循环次数增加，高岭土土体轴向应变逐渐增大，模拟与文献试验结果基本一致；循环加载阶段轴向应变增幅逐渐加大，循环卸载阶段轴向应变增幅逐渐减小，体现土体在循环载荷作用下的应变特征。

3 小应变黏土亚塑性本构模型子程序的工程应用

京张高铁官厅段桩基础桩端为厚层灰褐色湖相沉积土，为分析其在列车动循环载荷作用下变形特征，经钻孔取芯获得原状土体。采用南京水利科学研究院多功能循环三轴试验仪GDS(global digital systems)开展长期循环荷载作用下湖相沉积黏土变形试验，同时采用PLAXIS 有限元亚塑性本构子程序对其进行模拟分析。湖相沉积黏土原状土体亚塑性模型参数见表3。

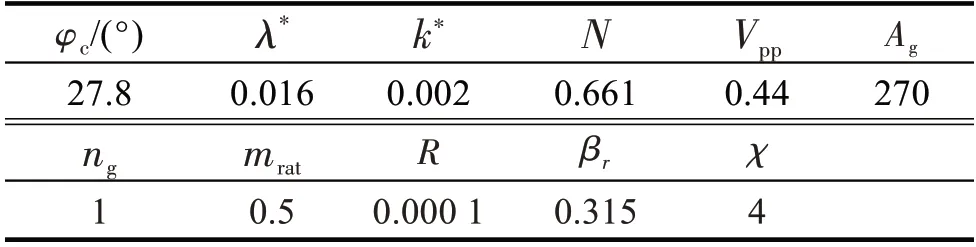
表3 湖相沉积黏土原状土体亚塑性模型材料参数Tab.3 Material parameters of subplasticity model of undisturbed lacustrine sediments

图5 为300，400，500 kPa 围压下湖相沉积原状黏土固结排水三轴试验与模拟结果。由图5 可看出：湖相沉积土体呈现硬化特征，在土体峰值强度及应力应变趋势上，模拟与试验结果一致性较好；数值模拟对原状土体前期小应变内的非线性行为预测较好，但对于偏应力峰值的预测较试验提前。

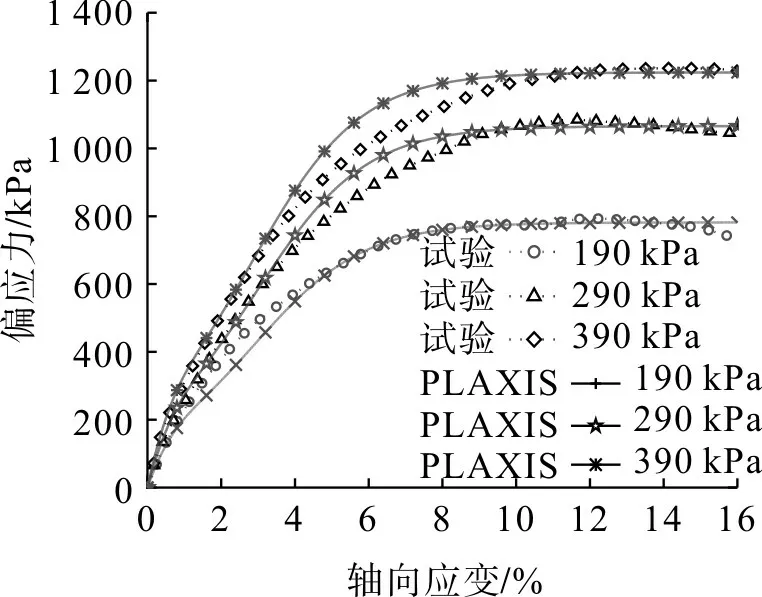
图5 湖相沉积原状黏土轴向应变与偏应力关系曲线Fig.5 Curves of relationship between axial strain and deviatoric stress of undisturbed clay in lacustrine sediments

为研究循环载荷作用下湖相沉积土体变形响应，选取试样在400 kPa 的围压下固结，经试验测定初始孔隙比e0= 0.703，然后施加半正弦波动应力qamp= 240 kPa，轴向应变随循环次数N的变化见图6。

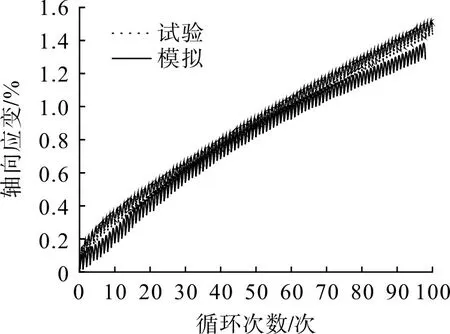
图6 循环周期与轴向应变关系曲线Fig.6 Curves of relationship between cycle period and axial strain

由图6 可知：随N的增加湖相沉积黏土变形逐渐增大；N<40 时，轴向变形模拟结果小于试验结果；N>40时，轴向应变模拟结果逐渐趋近试验结果。湖相沉积原状黏土轴向应变与偏应力关系曲线如图7。

图7 轴向应变与偏应力关系曲线Fig.7 Curves of relationship between axial strain and deviatoric stress

由图7可看出，在循环载荷作用下，模拟结果能较好体现轴向应变的变形过程，与试验结果基本一致，表明基于PLAXIS平台二次开发的小应变亚塑性黏土本构模型程序在实际工程中的适用性。

4 结论

基于PLAXIS有限元，利用二次开发接口开发小应变亚塑性黏土本构模型子程序，模拟分析常规三轴试验和循环三轴试验过程中轴向应变与偏应力关系，模拟结果与文献试验结果基本一致，证明了二次开发子程序模拟结果的合理可靠；采用子程序模拟分析官厅地区湖相沉积土三轴试验过程中的轴向应变与偏应力关系，结果显示在循环载荷作用下，模拟结果能较好体现轴向应变的变形过程，与试验结果基本一致。表明二次开发的PLAXIS子程序可使小应变亚塑性黏土本构模型方便地应用于工程计算中，扩大了PLAXIS在土木工程有限元分析中的应用范围。