改进稀疏表示与积化能量和的多聚焦图像融合*
2022-01-24张贵仓苏金凤
张贵仓,王 静,苏金凤
(西北师范大学数学与统计学院,甘肃 兰州 730070)
1 引言
图像融合的目的是将来自多个传感器的图像的冗余和互补信息集成到一幅新图像中,更适合人类或机器感知[1]。其中,多聚焦图像融合是图像融合的重要分支,近几十年来,多聚焦图像融合一直是研究的热点[2,3]。
到目前为止,根据不同的处理域可以将图像融合算法分为:基于空间域的图像融合算法和基于变换域的图像融合算法[4]。基于空间域的图像融合算法有方差、加权平均和空间频率[5]等。虽然这些算法可以部分区分聚焦区域和离焦区域,但由于分辨能力有限,导致得到的融合图像通常具有较高的空间失真和较低的信噪比[6 - 8]。基于变换域的非下采样轮廓波变换NSCT(Non-Sampled Contourlet Transform)[9]在图像融合中得到广泛的应用,但它具有很高的计算复杂度,限制了其在实际场景中的应用。因此,近年来,Easley等[10]通过非下采样金字塔滤波器NSPF(Nonsub-Sampled Pyramid Filters)和改进的剪切波滤波器组SFB(Shearlet Filte Banks),提出了非下采样剪切波变换NSST(Non-Sampled Shearlet Transform),不仅解决了传统变换的所有问题,而且具有多尺度局部性、各向异性和计算复杂度低等优点[11 - 13]。
另一方面,好的融合算法还依赖于有效的融合策略。传统的低频子带融合方法是取系数的加权平均值,这对图像融合的对比度和分辨率有较大影响[11]。Liu等[12]成功地将结构张量和NSST应用于CT和MRI图像的融合,但是他们使用简单的平均融合规则融合了低频子带系数。同样,处理高频子带系数最简单且有效的方法之一是使用最大绝对值融合规则[13]。但是,源图像之间的某些冗余信息很容易丢失,一些“伪影”被引入到融合图像中。拉普拉斯能量和[14]与修正拉普拉斯能量和[15]常用于捕获高频子带中的所有显著特征。迄今为止,研究人员提出的多种合理的融合方法中,稀疏表示SR(Sparse Representation)在图像融合领域中得到了广泛的应用[16]。Yang等[17]提出基于SR的图像融合框架,并使用最大值融合规则计算稀疏系数。Liu等[18]提出自适应的稀疏表示图像融合,并用OMP(Orthogonal Matching Pursuit)算法计算稀疏系数。Liu等[19]提出基于卷积稀疏表示的融合框架,将源图像通过卷积稀疏表示分解为基础层和细节层,再分别对基础层和细节层进行融合,得到融合图像。Liu等[20]提出基于SR和NSCT的图像融合算法,提高了融合图像的亮度,但一些细节存在缺陷。杨勇等[21]提出基于NSST和SR的图像融合算法,得到的融合图像在亮度上有所改善,但存在虚假的边缘信息。本文提出基于改进SR的融合规则,增强了图像的清晰度。同时,为了增强图像锐化的细节信息并改善图像的亮度,本文提出积化能量和算法。
本文采用NSST变换将改进SR与积化能量和相结合,提出改进SR与积化能量和的多聚焦图像融合算法。NSST用于分解多聚焦源图像,以获得低频子带系数和高频子带系数。对于低频子带系数,采用基于改进SR的融合算法获得低频融合系数;对于高频子带系数,提出积化能量和的融合算法,以获得高频融合系数。最后,使用NSST的逆变换获得多聚焦融合图像。该融合算法可以最大程度地提取重要显著特征的细节信息。
2 相关研究
2.1 非下采样剪切波变换
NSST分为2个步骤:第1步通过NSPF对多聚焦源图像进行l级分解,获得低频子带系数和高频子带系数;第2步通过SFB对图像进行多尺度和多方向的分解[14]。实际上,用NSPF可得到粗糙的多尺度分解图像,即对源图像进行l级、k方向的分解,得到与源图像大小相同的一个低频子带系数Ll和多个高频子带系数Hl,k,其中,Hl,k表示第l级、k方向的高频子带系数。图1是2级NSST分解的示意图。

Figure 1 NSST分解示意图图1 NSST decomposition
2.2 稀疏表示理论
SR模型基于以下假设:可将多个聚焦信号表示或近似为冗余字典中几个原子的线性组合。给定一个冗余字典D∈Rn×T(n (1) 在多聚焦图像融合中,场景图中相同位置的图像由于聚焦和成像机制的不同,聚焦图像存在差异,导致每幅图像包含的细节信息不同,如纹理、边缘等[17]。传统的低频子带融合方法有很多局限性,例如,绝对值解的系数取大法易丢失一些细节信息,等权值加权平均法在某些区域可能会引起融合图像亮度的显著下降,邻域能量取大法容易引入一些噪声[18]。因此,本文提出基于改进SR的低频系数融合规则。 (2) (3) (4) (5) 其中,D是局部自适应字典,ε是允许误差。 (6) (7) (8) 稀疏系数融合V-E规则如式(9)所示: (9) (10) (11) 图像通常可以被视为二维分段平滑信号,而高频分量中也包含许多能量与边缘细节信息,在多聚焦图像融合中,由于源图像的成像机制不同,聚焦程度不同,导致生成的图像不同。传统的高频融合规则基于拉普拉斯能量和,经常会带来融合图像能量损失,亮度也易急剧下降,从而导致视觉感知体验下降。为了改善融合图像亮度获得具有丰富细节信息的融合图像,本文提出了积化能量和的高频子带系数融合规则。 为提取高频子带系数的能量,本文定义了局部加权能量LWE(Local Weighted Energy),如式(12)所示: (12) (13) 为了获取更详细的细节信息,本文定义了局部加权8邻域修正拉普拉斯能量和WSML(locally Weighted eight neighborhood Modified Laplace energy Sum),如式(14)所示: (14) |2r(i,j)-r(i,j-1)-r(i,j+1)|+ (15) 高频段的最终积化能量和定义为LWE和WSML的乘积,如式(16)所示: (16) 本文使用NSST变换将改进SR与积化能量和相结合,以实现不同场景和焦距的多聚焦图像融合。假设A和B是2幅已配准且具有不同聚焦源的输入多聚焦图像,F为最终的融合图像。 具体的融合步骤可分为如下3步: 融合算法过程如图2所示。 Figure 2 Process of multi-focus image fusion 图2 多聚焦图像融合过程 为了验证本文算法的可行性,本节选取5对严格配准且大小为256×256的图像(如图3所示),利用Matlab(2016a)进行实验,并与目前流行的5种多聚焦图像融合算法进行比较,这5种算法分别是基于稀疏表示SR的图像融合算法[17]、基于自适应稀疏表示ASR (Adaptive Sparse Representation)的图像融合算法[18]、基于卷积稀疏表示CSR (Convolutional Sparse Representation)的图像融合算法[19]、基于非下采样轮廓波变换NSCT和稀疏表示SR的图像融合算法[20]、基于非下采样剪切波变换NSST和稀疏表示SR的图像融合算法[21]。其中本文实验参数设置如下:NSST分解级数l和方向数k设置为[3,3,4,4];稀疏编码中,块大小是8×8,步长s=1。 Figure 3 Multi-focus image pairs in experiment图3 实验使用的多聚焦图像对 由于在真实场景中没有参考图像,因此对融合图像的质量进行定量评估并非易事。近年来,研究人员提出了多种图像评估方案,但这些方案褒贬不一,无法确定哪一种评估方案最准确。因此,研究人员往往采用多种方案并行的方式对融合结果进行客观评估,本文采用最常用且效果较好的5个指标来验证本文算法的有效性,其分别为:互信息MI(Mutual Information)、边缘强度QAB/F(Edge Strength)、平均梯度AG(Average Gradient)、峰值信噪比PSNR(Peak Signal-to-Noise Ratio)和结构相似度SSIM(Structural Similarity Idnex)。其中,MI可计算源图像有多少信息移动到融合图像中[16];QAB/F可度量有多少边缘信息从源图像移动到图像融合中[17];AG反映了图像对细节、纹理显示的能力[18];PSNR值的大小表示融合图像的失真程度,值越大则效果越好[19];SSIM可以权衡融合图像与源图像之间的结构相似性[21]。因此,上述5个评价指标的值越大,融合图像越清晰,融合图像的效果越好。 图3是不同场景下的多聚焦图像对(5对),图像均是对部分区域进行聚焦,其他区域散焦。图4展示了采用不同算法的融合图像。其中,第1列为SR的融合结果,第2列为ASR的融合结果,第3列为CSR的融合结果,第4列为NSCT_SR的融合结果,第5列为NSST_SR的融合结果,第6列为本文算法的融合结果。6种算法都能得到最终融合的图像,并得到有效的信息,仔细观察可以发现:第1行第1~2列的2幅图像没有很好地将右聚焦源图像的信息进行融合,导致融合后的图像清晰度降低;第1行第3~5列的3幅图像丢失了部分纹理信息,对比度下降;第1行第6列的图像则很好地保留了图像的细节及纹理等信息,同时提高了图像的清晰度和对比度,融合效果较好。第2行第1~6列的6幅图像,学生的头部在场景中有轻微的运动,我们观察能看到6种算法的融合图像中学生头部都会受到不希望出现的伪影的影响,但第2行第6列的图像可以获得很好的视觉效果。第3行第1~2列的2幅图像中老虎的脚部发白,图像的清晰度下降;第3行第3~5列的3幅图像整幅图像清晰度提高,却丢失了部分纹理信息; 第3行第6列的融合图像则提高了图像的清晰度,较好地保留了纹理信息,融合效果比较理想。第4行第1~2列的2幅图像的闹钟和书桌的边缘出现了严重的虚影,融合效果较差;第4行第3~5列的3幅图像均较好地保留了源图像特征,但损失了部分细节信息;第4行第6列的融合图像聚焦区域的边缘处融合效果比较理想。第5行第1~6列的6幅图像中,气球在场景中有轻微的运动,融合图像的清晰度越来越高;第5行第6列的融合图像的清晰度最高,聚焦区域的边缘处融合效果较好。 Figure 4 Fusion results multi-focus image pairs with different algorithms图4 多聚焦图像对采用不同算法的融合结果 表1列出了5对多聚焦图像融合效果的客观评价结果。从表1中结果可以发现,SR算法的AG和MI评价指标总是最低的,相反PSNR评价指标总是比较高,这意味着它对融合图像中错误引入的噪声具有鲁棒性,但是可能会丢失一些细节信息;ASR和CSR算法的AG、QAB/F、MI和SSIM的值均优于SR算法的客观评价指标,说明融合的图像在清晰度、对比度上有较大提升,但细节和纹理等信息较模糊,图像容易失真;NSST_SR算法和NSCT_SR算法几乎可以得到较高的AG和MI,反而PSNR指标要相对低一些,这表明虽然这2种算法可以通过4级分解提取足够的细节信息,但其对误配准、误聚焦具有较强的敏感度;本文在NSST_SR算法的基础上,对高频子带系数提出了一种符合视觉效果的融合算法,对低频子带系数提出了改进的稀疏表示融合算法, 其AG、MI、PSNR、SSIM和QAB/F指标均优于其他算法的,这表明本文算法不仅拥有对比算法的优点,而且还能抑制噪声,提高清晰度和对比度,较好地保留了图像的细节及纹理信息,是针对多聚焦图像的一种有效融合算法。 Table 1 Objective evaluation experimental results of image fusion 本文提出一种将改进SR与积化能量和相结合的多聚焦图像融合算法。首先将NSST应用于已处理的源图像,得到高频子带系数和低频子带系数。对低频子带系数提出了低频融合规则,即采用滑动窗口对低频图像划分,减少字典学习所需要的数据量,再利用基于改进SR的融合规则得到稀疏系数,最终获得低频融合系数,这使得低频融合中的关键问题得以解决,即细节提取;另一方面,对于高频子带系数提出积化能量和的融合规则,以保证图像的亮度与能量的保持。实验分析表明,与经典算法相比,本文所提融合算法得到的结果可保留更多细节信息,具有更好的视觉效果,是一种有效的融合算法。

3 图像融合算法具体实现
3.1 基于改进稀疏表示的低频系数融合规则
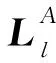
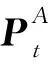
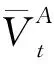
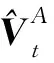
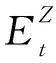
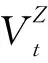
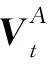

3.2 基于积化能量和的高频系数融合规则

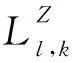

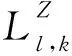

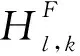
3.3 融合算法步骤
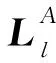

4 实验结果与分析



5 结束语
