一种精确缩略图保持的图像加密方案*

侯兴旺，赵若宇，张玉书

(南京航空航天大学计算机科学与技术学院，江苏 南京 211106)

1 引言

随着互联网的高速发展和各种电子设备的普及，人们越来越多地使用手机、相机等通过拍照来记录生活。照片逐渐增多，保存在本地会使得照片的分享和存储非常不便，为了更好地管理和存放照片，人们越来越多地将照片存储到云端，如阿里、百度和华为等提供的云存储服务平台。据估计，Facebook用户每天共享和上传的照片超过18亿张[1]。这些第三方的云服务商一方面为人们存储和管理照片提供了极大的便利，但是另一方面，人们的隐私却没有得到很好的保障。照片数据泄露的例子也层出不穷。例如，考拉征信非法提供身份证反照查询9 800多万次，非法获利3 800万元，这对人们的财产造成了极大的损失[2]，因此保护照片的隐私势在必行。

为了解决上述问题，学者们提出了一系列的图像加密方案[3 - 11]，如基于置乱的加密、基于变换域的加密和基于秘密分割的秘密共享加密等。

基于置乱的加密是将原图的像素打乱，改变原像素之间的相关性和空间关系，使图像变得肉眼无法识别、杂乱无序来达到加密的效果。目前置乱的方案有：基于Arnold置乱及其扩展、基于正交拉丁方的图像置乱变换、基于幻方的图像置乱变换和基于随机数排列的置换等。Arnold置乱主要是将原始的图像按照预先设定的规则，进行打乱次序的操作。打乱次序指的是对图像进行坐标变换，由于置乱只是改变图像像素的顺序，没有改变像素值，并且置乱具有周期性，已有大量的研究表明，置乱加密不能抵御统计攻击，因此安全性不足，

基于变换域的图像加密是改变变换域中的系数，而系数的改变可能使像素值发生改变，因此可以通过对变换域的系数进行处理来完成图像的加密。基于变换域的加密方案在加密和解密时存在精度的丢失，导致解密后的图像与原图不一致。以JPEG和JPEG2000编码为例，结合压缩的加密算法应当在变换域系数的量化之后再进行置乱、替换和扩散，即通过量化使图像的细节信息的高频信息隐藏，图像的低频信息损失得少，尽可能地保持图像的质量，并且不影响图像的加密效果。如果仅仅将系数的位置置乱，或者改变量化后系数的符号，攻击者可以通过对比明文和密文的图像的变换域系数得到置乱的规律，从而破解加密算法。如果对频域的所有量化后的系数进行全局置乱、扩散和代换，那么就会毁坏系数的分布规律，降低压缩效果。综上，在变换域系数被量化之前加密效果较差，但是在变换域系数量化后使用局部的置乱、扩散和代换，可以有效地减少加密的数据量，提高加密效率，并且降低加密对压缩的影响，提高图像质量。

基于秘密分割和秘密共享的图像加密算法可以被用来部分缓和这个问题。该加密算法是将明文图像分成若干份，每份称为一幅影子图像，这些影子图像被分给不同的保存者，只有一定数量的秘密保存者提供影子图像时，才能重构图像。秘密共享的优势在于，小于特定数量的影子图像泄露不会造成秘密的泄露，也不会泄露明文信息，并且不需要全部的共享者提供信息就可重构明文。文献[9]提出了一种基于秘密分割和秘密共享的图像加密算法，它将变换域量化后的系数进行分割，生成若干幅影子图像。虽然该加密算法经过仔细辨认可以分辨部分图像，能够部分缓和上述方案中的问题，但是该方案将加密图像分为若干不同的部分，增加了图像的存储量。

这些加密方案能够很好地保护照片的隐私，安全性也得到一定的保障。然而，这些方案却没有关注图像的可用性。例如，人们把加密的照片传到云端，由于无法识别照片的内容，当人们进行浏览时，不能直接在云平台上进行删改等操作，需下载到本地解密后才能进行，这给人们带来了不必要的麻烦，同时也增加了云服务商的负担。最近，研究人员提出了一种新的图像加密方案——缩略图保持加密方案，该方案通过保持像素块的和不变来达到密文缩略图与明文缩略图一致的加密效果，从而能够比较好地平衡隐私与可用性。Marohn等[12]提出一种基于置换操作的格式保持加密方案，该方案能够达到缩略图保持的效果，但是由于没有改变像素值，明文图像的像素值没有经过加密就暴露，使得图像安全性降低，并且这种置换使得图像压缩变得困难。Charles等[13]提出了一种近似的缩略图保持加密方案，该方案利用了人们对图像的识别能力，即人们见过一张照片后，当这张照片被扭曲或者模糊后依然能够区分它[14]。若这张照片是人们自己制作或者拍摄的，则这个能力将会增强[15 - 18]。该方案中提出了2种加密方法DRPE(Dynamic Range Preserving)和LSB(Least Significant Bit)。这2种加密方法都是近似的保持缩略图，同时暴露像素块的平均值或者最大值，并且当加密和解密的动态空间选取不一致时，会使得解密失败。Tajik等[19]提出了一种精确的缩略图保持加密方案，如图1中的TPE(Thumbnail-Preserving Encryption)加密所示。

Figure 1 Ciphertext image and its thumbnail with different encryption schemes图1 不同加密方案下的密文图像及其缩略图

为此，本文提出一种新的精确缩略图保持加密方案，该方案是以3个像素为一组，适用于各种各样的照片云存储平台。该方案以块为单位，先分块；然后提取切割特征，加密切割特征；最后将切割特征转换成像素组。整个过程保持像素值的和不变，并且加密过程都是可逆的，因此密文图像的缩略图和明文缩略图完全一致，并且图像通过解密可以无损恢复。本文的主要贡献如下所示：

(1)提出了一种新的缩略图保持加密方案，相比Tajik等人提出的方案，本文方案能够以3个像素为一组进行加密操作，提高了效率和安全性。

(2)对本文提出的切割特征方法进行了形象化的解释。

(3)基于本文提出的方案对不同大小的图像进行了实验，以获得加密效果与块大小的最佳组合，为以后类似的加密方案提供参考。

2 预备知识

本节主要介绍一些基础的定义，这些定义将会从根本上解释本文提出的方案。

2.1 基础定义

定义1一个加密方案被称作是格式保留加密FPE(Format Preserving Encryption)[20]，如果对于一个加密算法有式(1)成立：

E:K×N×T×→∪{∅}

(1)

其中,集合K,N,T和为相应的密钥空间、格式空间、调整空间和值域。对任意的X∈，K∈K,N∈N,T∈T, 记当且仅当N∉N,X∉。

定义2X是具有某种格式的一个切片[20]，如果对于任意的(X,T)∈×T, 有式(2)成立：

(2)

定义3一个图像加密方案被称作是缩略图保持加密方案[19]，如果对于任意的K,T,M，式(3)成立：

DecK(EncK(T,M))=M,

Φ(EncK(T,M))=Φ(M)

(3)

定义4函数y=f(x)被称为单向函数。当已知x，很容易计算出y，但是在已知y的情况下，计算出x=f-1(y)是极其困难的。

(4)

的绝对值小于λ。

定义8一个加密方案具有NR-安全性[19]，如果关于任何NR区分者都满足定义7。

2.2 分割法

分割法是3个像素为一组，利用他们之间的相互关系进行变换。假设现有像素组(x,y,z)，对其进行和保持变换。

首先，利用式(5)计算像素组的分割位并记录为(p1,p2)。

(5)

然后，将(p1,p2)加密为(p′1,p′2)，最后由(p′1,p′2)计算出(x′,y′,z′)。计算(x′,y′,z′)就是式(5)的逆过程，如式(6)所示：

(6)

因为整个过程是和保持的，所以sum=x+y+z作为一个已知量。

下面用一个简单的例子来说明加密过程,以像素组(4,3,1)为例：

(1)首先由(4,3,1)计算出相应的位置信息如式(7)所示：

(7)

所以,(p1,p2)为(4,7)。

(2)接着将(p1,p2)加密，这个加密算法可以采取任意的加密算法，只要加密解密域合理即可。假设将(4,7)加密为(2,6)，也就是(p′1,p′2)为(2,6)。

(3)最后(p′1,p′2)由式(8)得到加密后的像素组：

(8)

最终将(4,3,1)加密为(2,4,2)。图2可以更加清晰地说明这个过程，图中黑色圆的个数表示像素组中像素值的和，竖线表示分隔符，2个分割符之间黑色圆的个数表示像素值。

Figure 2 Flowchart of pixel group encryption 图2 像素组加密流程图

3 基于分割法的图像加密方案

本文方案利用分割法以3个像素为一个基本单位进行加密，根据不同的需求可以将明文图像加密成具有不同视觉效果的密文图像。对于任意图像加密，首先将图像分成(B×B)的块，然后把每一个大块划分为大小为(b×b)的小块。这样每一个大块都会被划分成((B/b)×(B/b))个像素块网格，加密方案就在像素块网格上进行操作。下面详细介绍方案的步骤。

3.1 图像分块

将明文图像分成(B×B)的大块，用户可以根据自己的需要选择不同的块大小。块大小的选择直接会影响密文图像的效果，如果选择的块过大，图像缩略图的效果就不是很好，会导致密文被明显地分为几个大块的雪花状，从而无法正确猜测明文图像的内容，那么缩略图发挥的作用就不是很大，但是保密效果却得到了良好的体现；如果选择的块太小，会导致密文图像暴露过多的细节信息，缩略图发挥很好的作用，但是隐私却没有得到保障。显然，选择块的大小是非常重要的，如何选择块的大小将在后面的实验中展示。

3.2 利用分割法进行加密

当确定好块大小之后，就可以分块对图像进行加密，这个过程可以多线程进行，以提高加密效率。对于任意的(x,y,z)，其中x,y,z表示像素组中的像素值，密钥为key，具体加密步骤如下所示：

(1)首先由式(5)计算(p1,p2)，计算像素组和sum=x+y+z。

(2)通过加密算法把第(1)步得到的(p1,p2)经过加密得到(p′1,p′2)。

(3)利用(p′1,p′2)通过式(6)计算出(x′,y′,z′)。

(4)如果(x′,y′,z′)在密文域内则加密完成，(x′,y′,z′)就是密文的最终结果；否则key=key+1，返回第(2)步。

(5)重复上面的过程，直到所有的块都被加密完成。

(6)最后根据密钥key利用Fisher-Yate洗牌算法将大块内的像素打乱，完成一轮加密。

(7)根据需要可以进行轮加密。

接下来对上面步骤给出进一步的说明。第(2)步可以使用任意的加密算法进行加密，这一步将直接决定加密算法的安全性。这里明文域是0～sum，密文域同样是0～sum，这是格式保留的关键步骤。下面举一个最简单的映射作为加密函数来说明加密算法。通过随机数生成算法利用key生成一个0～sum的置换P,其中P表示一个置换矩阵。

把第(1)步得到的分割特征(p1,p2)经过置换得到(p′1,p′2)=(ap1,ap2)。首先来说明分割法是可以遍历像素和为sum的组合。对于任意的(x,y,z)，都有(p1,p2)与之对应；对于任意的和为sum的(p1,p2)，都可以根据式(6)得出(x,y,z)。接下来考虑一些特殊的情况，当(x,y,z)=(0,0,sum)时，表示成示意图如图3所示。

Figure 3 Special case of split method图3 分割法特殊情况

这时p1=p2=sum，那么分割标记就会重合到一起，也就是图3中最后的2条黑线的位置，分别表示p1和p2的大小，这样任意的像素组数目都会有与之对应的(p1,p2)，反之亦然。所以，分割法会遍历所有的密文域。

最后使用Fisher-Yate洗牌算法进行置乱，由于加密方案要保持缩略图，所以只能在块内打乱，才能保证整个块内的和在加密前后是不变的。

3.3 解密

因为加密过程是完全可逆的，所以解密就是加密的逆过程，下面简要说明解密步骤：

(1)根据密钥key利用Fisher- Yate生成逆置换，将打乱后的图像进行初次恢复。

(2)对于任意的(x′,y′,z′)获得其(p′1,p′2)。

(3)通过解密算法把第(2)步得到的(p′1,p′2)经过解密得到(p1,p2)。

(4)由(p1,p2)得出(x,y,z)并判断是否在加密域内，若在，则第(1)轮解密完成；否则key=key+1，返回第(3)步。

(5)重复上面的过程直到所有的块都被解密完成。

3.4 安全性分析

为了更好地分析算法的安全性，根据文献[19]将加密方案建模为马尔可夫链模型，它的安全性与马尔可夫链的混合时间相关。

加密方案可以看作是一个马尔可夫链。对于任意像素组和为sum，A表示和为sum的所有像素组的集合。这些像素组构成马尔可夫链的一个状态，马尔可夫链的转移矩阵代表从一个状态转移到另一个状态的概率，也就是由一个像素组加密为另一个像素组的概率。这个概率由加密算法和Fisher-Yate洗牌算法的概率确定，由于每个加密算法和洗牌算法对最后的结果是“公平的”， 因此各个状态之间的转移概率是相同的。

马尔可夫链的混合时间是当马尔可夫链达到稳态所需要的时间，在本文加密方案中就是加密达到一定安全要求所需要的轮数，由文献[19]可得：

(9)

4 实验结果分析

本节从2方面进行实验分析，一方面通过实验得出块大小与加密时间的关系，另一方面对不同大小的图像，分别以不同的块大小进行加密，观察密文图像的结果，得出合适的加密块大小。

4.1 块大小与加解密时间的关系

本节实验分别对512×512和1024×1024的图像分不同的块大小进行加密和解密，记录时间，结果如图4和图5所示。

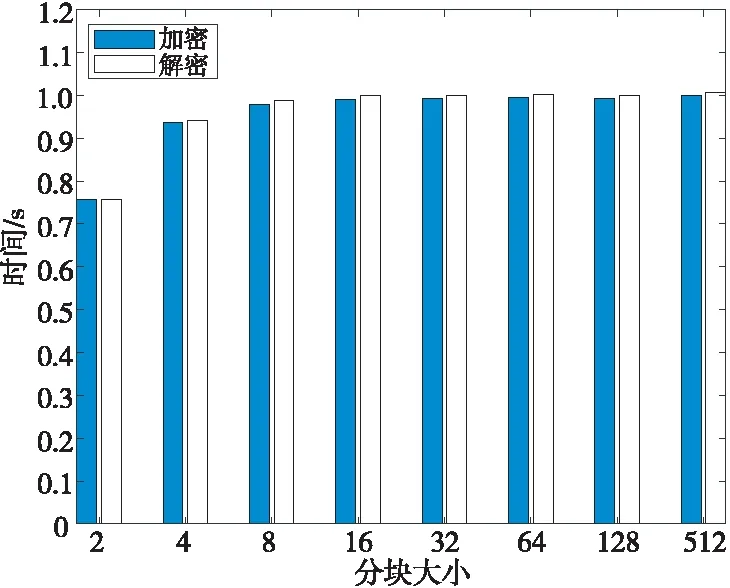
Figure 4 Encryption and decryption time of 512×512 image图4 512×512 图像加解密时间

Figure 5 Encryption and decryption time of 1024×1024 image图5 1024×1024 图像加解密时间

实验对512×512和1024×1024的图像进行加密和解密操作，对512×512大小的图像，实验将图像分为块边长为2,4,8,16,32,64和512的图像块；对1024×1024大小的图像，实验将图像分为块边长为2,4,8,16,32,64,512和1 024的图像块。通过图4和图5，可以看出，加密和解密的时间基本相同，解密时间略比加密时间长；当块大小边长小于8时，加密和解密时间增加明显，当块边长大于8时，加密和解密时间基本保持稳定。从整体上看，1024×1024大小的图像加解密时间明显大于512×512的，但是并没有超过4倍，可见加解密时间与像素数量并不是简单的线性关系。

4.2 加密块大小对密文图像的影响

本节实验分别对512×512和1024×1024的图像分不同的块大小进行加密，对密文图像进行视觉上的观察，如图6所示。

Figure 6 Effect of different block sizes on ciphertext图6 不同块大小对密文图像的影响

图6中块边长大小依次为8,16,32,64,128和512。通过观察可以看出，当块边长为8和16时，图像细节展现得非常多，很明显地可以估计出图中人物，所以隐私泄露得较多；当块边长为32时，通过密文图像内容，可以推测到原始图像的大致内容，并且也没有透露过多其他的隐私，很好地平衡了图像的隐私和可用性；当块边长为64时，512×512大小的图像已经无法辨认，1024×1024大小的图像依稀可以辨别图中内容；当块边长大于64时，512×512和1024×1024的图像均无法辨认。甚至当块大小为图像大小时，加密图像就呈现雪花状，完全无法辨认。通过这个实验可以得出，当图像较小时，选择块边长为32，当图像较大时，可以选择32或64作为加密块的边长，都可以很好地平衡图像隐私和可用性。并且实验还得出，如果想要实现类似于传统加密方案的效果，可以将块大小选择为图像大小，以达到完全加密的效果。

4.3 不同块大小缩略图的PSNR值

本节分别对256×256，512×512，768×768和1024×1024大小的图像进行实验，并将得到的加密缩略图分别与明文缩略图进行比较得出各自的PSNR，如表1～表4所示，其中“m-n”表示图像大小为m×m,加密块大小为n，例如“256-4”表示图像大小为256×256，加密块的大小为4。

Table 1 PSNR of the 256×256 encrypted images’ thumbnail

Table 2 PSNR of the 512×512 encrypted images’ thumbnail

Table 3 PSNR of the 768×768 encrypted images’ thumbnail

Table 4 PSNR of the 1024×1024 encrypted images’ thumbnail

通过表1～表4可以看出，当分块较小时，PSNR具有较高的值，都超过30 db，甚至有的超过40 db，并且随着图像尺寸的增大，PSNR在逐渐增大；而当分块增大时，PSNR值逐渐降低，当将整幅图像作为一个加密块时，PSNR都低于20 db。实验表明，当块边长小于32时，加密图像缩略图能够保持与明文图像一致；而随着加密块的增大，加密图像缩略图和明文图像的缩略图相差较大，逐渐达到类似全部加密的效果。

5 结束语

本文针对如何平衡图像在云存储上的隐私与可用性问题进行研究，提出了一种精确的缩略图保持加密方案，该方案能够很好地平衡图像的隐私与可用性，一方面对图像进行了加密，使得图像中的具体细节不可识别，另一方面密文图像保持了与明文图像一致的缩略图，方便用户在云存储平台进行管理。并且，该方案可以灵活地选择加密块大小，满足用户对加密后图像的各种需求。最后，通过实验表明，本文提出的方案具有很好的效率和可用性。