改进小波软阈值函数在图像去噪中的研究应用*

徐景秀,张 青

(黄冈师范学院计算机学院，湖北 黄冈 438000)

1 引言

数字图像作为人类活动中常用的信息载体，在日常生活中扮演着重要的角色，数字图像处理是医疗及科研教学中必不可少的技术手段。然而受相关条件影响，数字图像在生成、传输以及压缩过程中容易受到外来噪声干扰，使图像边缘和纹理细节变得模糊，不利于图像信息的识别和读取[1]。因此，为进一步提升图像视觉效果和图像质量，挖掘和利用图像内部信息，必须尽量降低图像噪声的影响。

目前常用的图像去噪算法可以分为空间域去噪算法和变换域去噪算法。常见的空间域去噪算法主要有均值滤波、中值滤波、双边滤波、非局部均值滤波以及它们的改进算法等[2]。由于算法原理的限制，空间域去噪算法容易模糊图像的边缘和纹理等细节，且对于不同种类的噪声去除效果不同[3]。变换域去噪算法主要有傅里叶变换算法、小波变换去噪算法、曲波变换去噪算法和块匹配三维滤波BM3D(Block-Matching and 3D filtering)算法等[4]。变换域去噪算法由于参数多且很难选取合适的数值，导致去噪结果不理想，或者由于算法的复杂性导致算法效率低。还有目前较为流行的基于字典学习的去噪算法和基于深度学习的去噪算法等，然而深度学习和字典学习算法对噪声较为敏感，在强噪声情况下容易引入外来噪声，不利于细节信息的保护。

小波变换以傅里叶分析为基础，采用固定基对图像信号进行分解，具有较好的去噪效果和细节保持能力。然而合适的阈值和阈值函数的选取较为困难，从而限制了该方法在图像处理与信号分析等领域中的应用[5]。针对上述情况，国内外学者先后提出硬阈值函数HTF(Hard Threshold Function)小波变换、软阈值函STF(Soft Threshold Function)数小波变换以及半软阈值函数S-STF(Semi-Soft Threshold Function)小波变换方法，以及针对不同使用条件的阈值[6]。然而，由于既有阈值函数(硬阈值函数、软阈值函数等)自身原因，在阈值位置附近的重构信号和原始信号差异较大，导致重构图像失真，不利于图像质量的提升[7]。而常规的改进算法都是改进阈值函数的连续性，没有考虑阈值的适应性，且对阈值范围内的小波系数变化也未深入研究。

本文对小波变换的阈值及阈值函数进行改进，改进后的阈值自适应性更强，能够适应不同层中噪声对应小波系数分布情况，且改进后的阈值函数连续性更好，在阈值位置处更为平滑，计算过程更为稳定。实验结果表明，改进后方法的去噪结果峰值性噪比和结构相似度更好，图像细节纹理更清晰。

2 小波变换及图像去噪

2.1 基本理论

小波变换属于空间-频率的一种变换，通过缩放以及平移等方式实现图像的多尺度分解[8]，从而分离有效信号和噪声，其计算如式(1)所示：

(1)

则小波逆变换公式如式(2)所示：

(2)

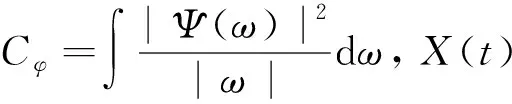
含噪图像经过小波变换后，对小波系数进行分解，可以得到不同频率范围的小波系数。图像有效信号通常分布于低频小波系数中，而噪声信号通常分布于高频小波系数中[9]。为实现有效信号和噪声信号的分离，小波阈值法采用合适的阈值识别噪声信号对应的小波系数并将其置零，最后应用阈值量化后的小波系数重构图像信号，从而实现图像噪声的去除[10]，其原理如图1所示。

Figure 1 Flow chart of wavelet threshold denoising图1 小波阈值法去噪示意图

2.2 常规阈值函数

在小波变换去噪过程中，阈值的选取尤为重要，合适的阈值将会使小波变换具有较好的去噪效果和纹理细节保持能力[11,12]。现有的阈值可以分为全局阈值和局部阈值，全局阈值为固定的阈值并应用于所有层的小波系数，局部阈值是根据某一层小波系数特征，有针对性地设定的当前层阈值[13]。相对而言，全局阈值计算效率高，但是去噪效果较差；局部阈值去噪效果好，但是计算效率低[14]。常用的阈值法主要包括通用阈值VSTS(VisuShrink ThreShold)、无偏似然估计阈值SSTS(SureShrink ThreShold)、HeurSure阈值HSTS(HeurSure ThreShold)和平移不变小波阈值等。目前较为常用的是Donoho等人[15]提出的通用阈值，如式(3)所示：

(3)

其中，(M*N)表示图像尺寸大小，σ表示估计的噪声标准差，其计算公式如式(4)所示：

(4)

其中，X表示小波变换的高频小波系数，Median表示中值函数。

阈值确定后，下一步对超过阈值范围的小波系数进行变换，常用方法主要包括硬阈值方法、软阈值方法以及半软阈值方法[16]。硬阈值函数HTF、软阈值函数STF和半软阈值函数S-STF分别如式(5)～式(7)所示：

(5)

(6)

(7)

其中，W表示式(1)中小波变换后的信号，δ表示通用阈值。

由上述公式和图2可知，硬阈值函数阈值范围外的小波系数保持不变；而软阈值函数将大于阈值绝对值的小波系数进行缩放；半软阈值函数中则存在2个阈值，分别为δ1和δ2。当2个阈值相等时，半软阈值函数转换为硬阈值函数，当δ2为无穷大时，半软阈值函数转化为软阈值函数[17]。相对于硬阈值和软阈值方法，半软阈值方法具有更好的适应性，能够取得更好的去噪效果。

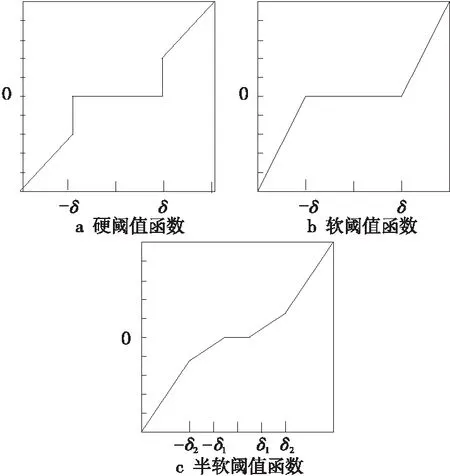
Figure 2 Schematic diagram of different threshold functions图2 不同的阈值函数示意图

半软阈值方法虽然能够改善硬阈值方法和软阈值方法的不足，但是具体应用中很难确定合适的双阈值，且计算时间相对较长，降低了效率，不利于方法的推广。

2.3 改进小波阈值函数

针对常规阈值函数的缺陷，王凤等人[18]在2019年提出了改进的小波阈值函数，其表达式如式(8)所示：

(8)

其中，k表示调节因子，用于调节阈值函数值。改进后的阈值函数在阈值位置处更连续，能够较好地解决原始小波系数和经过阈值约束的小波系数之间的偏差，具有较好的去噪效果。

2.4 新改进的小波软阈值函数

现有的阈值函数都是采用sign函数对小波系数进行变换，然而sign函数在间断点位置处易出现震荡，从而影响图像的去噪效果。因此，针对上述情况，本文采用和sign函数具有相似性质的tanh函数，该函数相对于sign函数而言，具有更好的连续性，在间断点位置处更为平滑，2个函数的形态变化如图3所示。

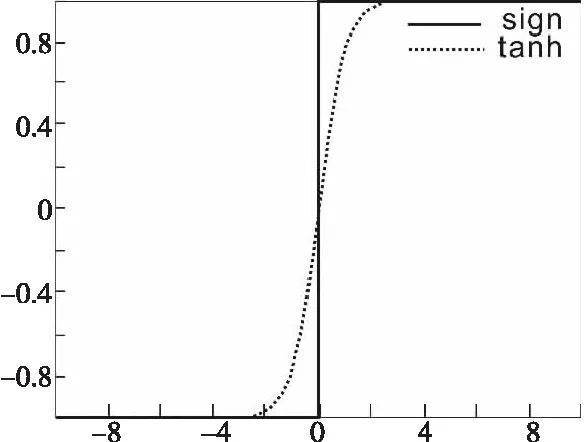
Figure 3 Schematic diagram of the change of sign function and tanh function图3 sign函数和tanh函数的变化示意图

由图3可知，tanh函数和sign函数整体保持一致，在间断点位置处，tanh函数的导数值也远远小于sign函数的导数值，因此能够更加准确细致地分辨信号和噪声所代表的小波系数。则新改进的阈值函数如式(9)所示：

(9)

其中，Wδ表示小波估计系数，W表示小波变换系数，δ表示小波阈值，k表示调节因子。其中调节参数用于维持阈值函数的稳定性及连续性，需要反复测试选取最优值。

常规的小波阈值函数以及文献[18]的改进小波软阈值函数都使用全局阈值，在所有层的小波变换中都采用相同的阈值[19]。然而实际变换中，随着小波分解层数的增加，图像噪声对应的小波变换模值逐渐变小，因而全局阈值容易误判噪声信号，从而降低去噪效果[20]。因此，本文采用一种随层变化的自适应小波阈值，该阈值随着小波变换层数的增加而逐渐减小，本文的自适应阈值如式(10)所示：

(10)

其中，i表示小波变换的当前层数，σ表示噪声标准差，M*N表示当前层的高频小波系数尺寸。式(10)中ln(e+2(1-i)-1)为衰减因子，随着小波变换层的增加而逐渐缩小，能够自适应调节阈值δi的大小，从而解决全局阈值在多层小波变换中对噪声信号误判的局限性，有效提升噪声小波系数的判断精度。

为进一步提升阈值函数在阈值位置的连续性和稳定性，避免阈值函数截断产生的吉布斯现象，本文在阈值绝对值范围内应用一个非线性函数对阈值函数进行逐步压缩，可以较好地解决原始小波系数和估计小波系数之间的偏差，将上述非线性函数和式(10)代入式(9)，则最终新改进的阈值函数表达式如式(11)所示：

(11)

其中，Wi表示小波变换的第i层系数，δi表示小波变换的第i层阈值，Wδi表示小波变换第i层的估计系数，T为压缩系数，取 [1，3]的整数，默认值为1。

将上述阈值函数与硬阈值函数、软阈值函数、半软阈值函数和文献[18]的改进软阈值函数的函数图像绘制在一个坐标系中，具体如图4所示。

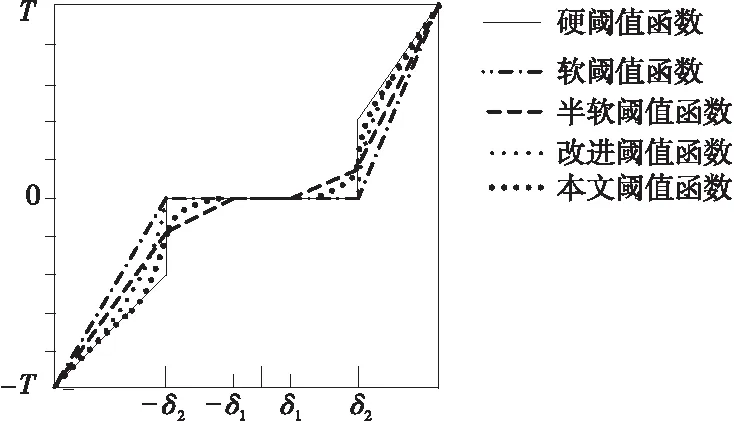
Figure 4 Schematic diagram of different threshold functions图4 不同阈值函数示意图

由图4可知，硬阈值函数在阈值位置处是间断点，左右不连续。软阈值函数由于缩放，与原始小波系数存在差异[21]。半软阈值函数虽然与原始小波系数偏差较小，但是在左右阈值位置处依旧不够连续。文献[18]的改进阈值函数在阈值范围以外，以硬阈值函数为趋势线，相对于硬、软阈值函数而言，具有较好的稳定性和连续性。本文提出的改进阈值函数，能够改善硬、软阈值函数在阈值位置处不连续的缺陷，相比半软阈值函数而言，参数更少，且比文献[18]的改进阈值函数连续性更好，进一步缩小了重构小波系数与原始小波系数之间的差异性。

从数学角度分析式(11)所示的新改进阈值函数连续性及偏差性，其公式推导如下所示：

推导连续性：

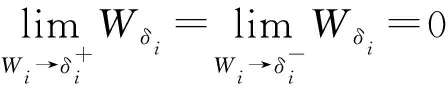
同理可知：

说明该阈值函数在δi处是连续的。

推导偏差性:

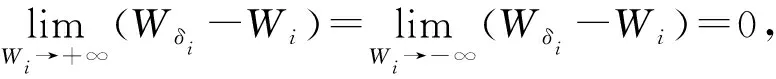
2.5 新改进的小波软阈值函数方法的去噪流程及步骤

算法1改进小波软阈值函数方法

输入：原始图像。

输出：去噪后图像。

步骤1对含噪图像进行小波多尺度变换；

步骤2采用式(4)估计噪声标准差；

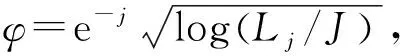
步骤4计算小波变换后每一层级的高频系数对应的标准差，然后采用式(10)计算自适应阈值；

步骤5采用式(11)对小波变换系数进行阈值处理，然后进行小波逆变换得到去噪后的图像。

其去噪流程如图5所示。

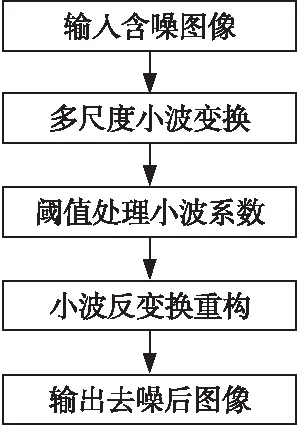
Figure 5 Flow chart of new improved wavelet soft threshold denoising 图5 新改进的小波软阈值去噪流程图

3 仿真实验及结果分析

本次实验根据本文方法开发相关程序模块,然后采用图6所示的8幅标准灰度图作为测试对象。在原始无噪图像上分别添加不同方差的高斯白噪进行仿真测试，应用峰值信噪比PSRN(Peak Signal-to-Noise Ratio)和结构相似度SSIM(Structural SIMilarity)来评价不同去噪方法的去噪能力和效果。

Figure 6 Standard test gray images图6 标准测试灰度图

3.1 调节参数的确定

由式(11)可知，调节参数k影响阈值函数的稳定性与连续性，合理有效地调节参数有利于提升去噪效果，因此，必须选定合适的调节参数。为验证和分析不同调节参数对去噪效果的影响，在Boat图像上添加标准差为10，20，30的高斯白噪进行测试，然后统计不同测试结果的PSNR值和SSIM值。不同测试结果的PSNR和SSIM数值随调节参数k变化的曲线如图7所示。由图7可知，不同噪声强度下，其PSNR和SSIM曲线变化不同，但是在调节参数k=60时，PSNR值和SSIM值最大，因此该最大值对应的调节参数就是本次实验的最优参数，因此在后续实验中可选择本次最优参数作为调节参数。

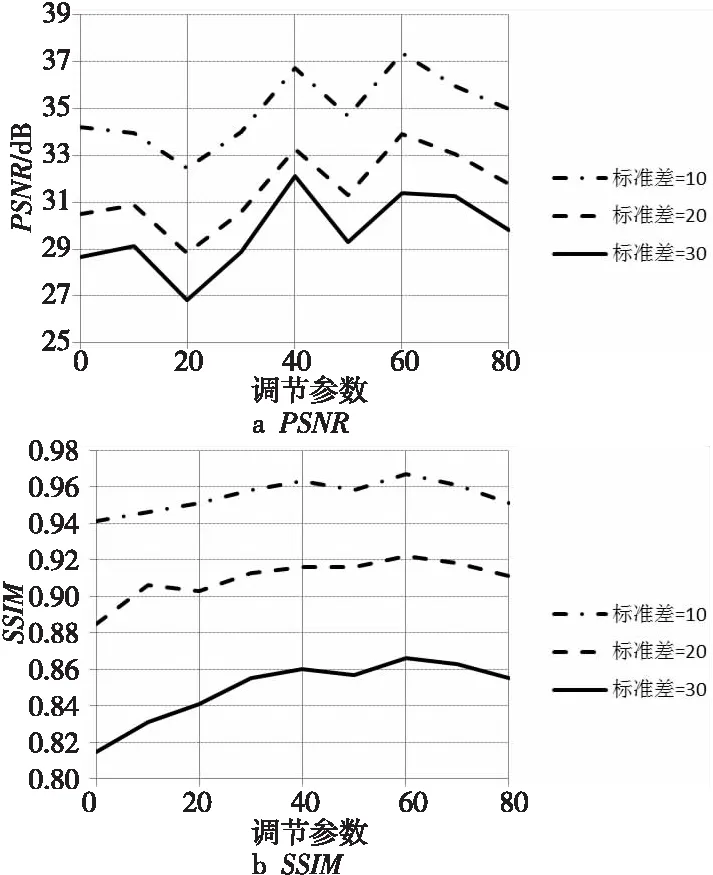
Figure 7 Schematic diagram of PSNR and SSIM changed with adjustment parameters图7 PSNR值和SSIM值随调节参数变化曲线示意图

3.2 小波阈值的对比分析与选取

为进一步分析本文的自适应阈值去噪方法去噪效果，在本文新的改进阈值函数中分别使用通用阈值VSTS、无偏似然估计阈值SSTS、HeurSure阈值HSTS和本文自适应阈值VATS(VAriable ThreShold)对Starfish和Butterfly 2幅图像进行测试，用PSNR值和SSIM值衡量不同阈值的去噪结果，则不同仿真结果的数据如表1所示。

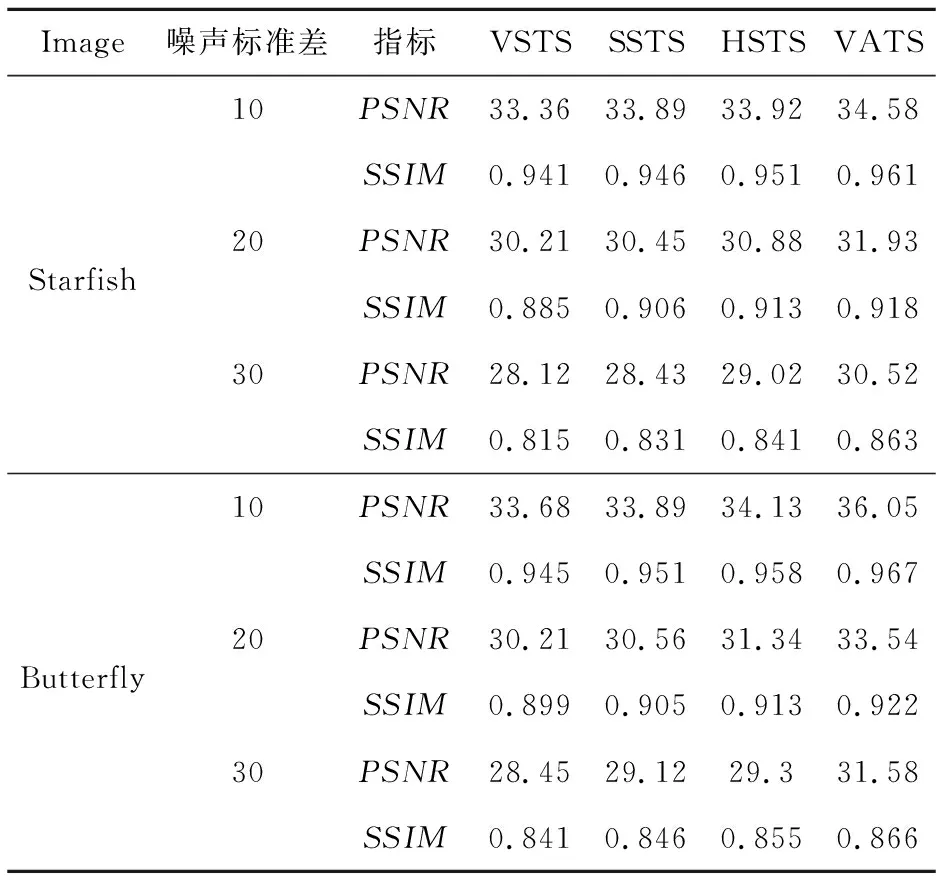
Table 1 PSNR and SSIM of denoising methods with different thresholds

由表1可知，不同的阈值的去噪方法的PSNR值和SSIM值不同，相对而言，本文的自适应阈值去噪方法优势最为明显，其去噪结果的PSNR值和SSIM值明显高于另外几种阈值去噪方法的，经过去噪之后，自适应阈值去噪方法的PSNR值平均提升至33.03，SSIM值平均提升至0.916。评价指标PSNR值和SSIM值的提升幅度方面，VSTS去噪方法的评价指标分别提升了35.5%和73.4%，SSTS去噪方法的评价指标分别提升了37.1%和76.4%，HSTS去噪方法的评价指标分别提升了38.8%和77.9%，本文阈值去噪方法的评价指标平均提升幅度达到48%和80.6%，表明本文VATS阈值去噪方法去噪效果最好。

3.3 不同去噪方法结果分析

为进一步分析本文去噪方法的效果，在Baboon、Bridge、C.man 3幅图像上添加不同噪声强度的高斯噪声，分别采用基于自适应阈值的硬阈值函数HTF、软阈值函数STF、半软阈值函数S-STF、文献[18]的改进阈值函数ITF(Improved Threshold Function)和本文新改进的软阈值函数进行测试，统计所有实验的PSNR值和SSIM值，结果如表2所示。

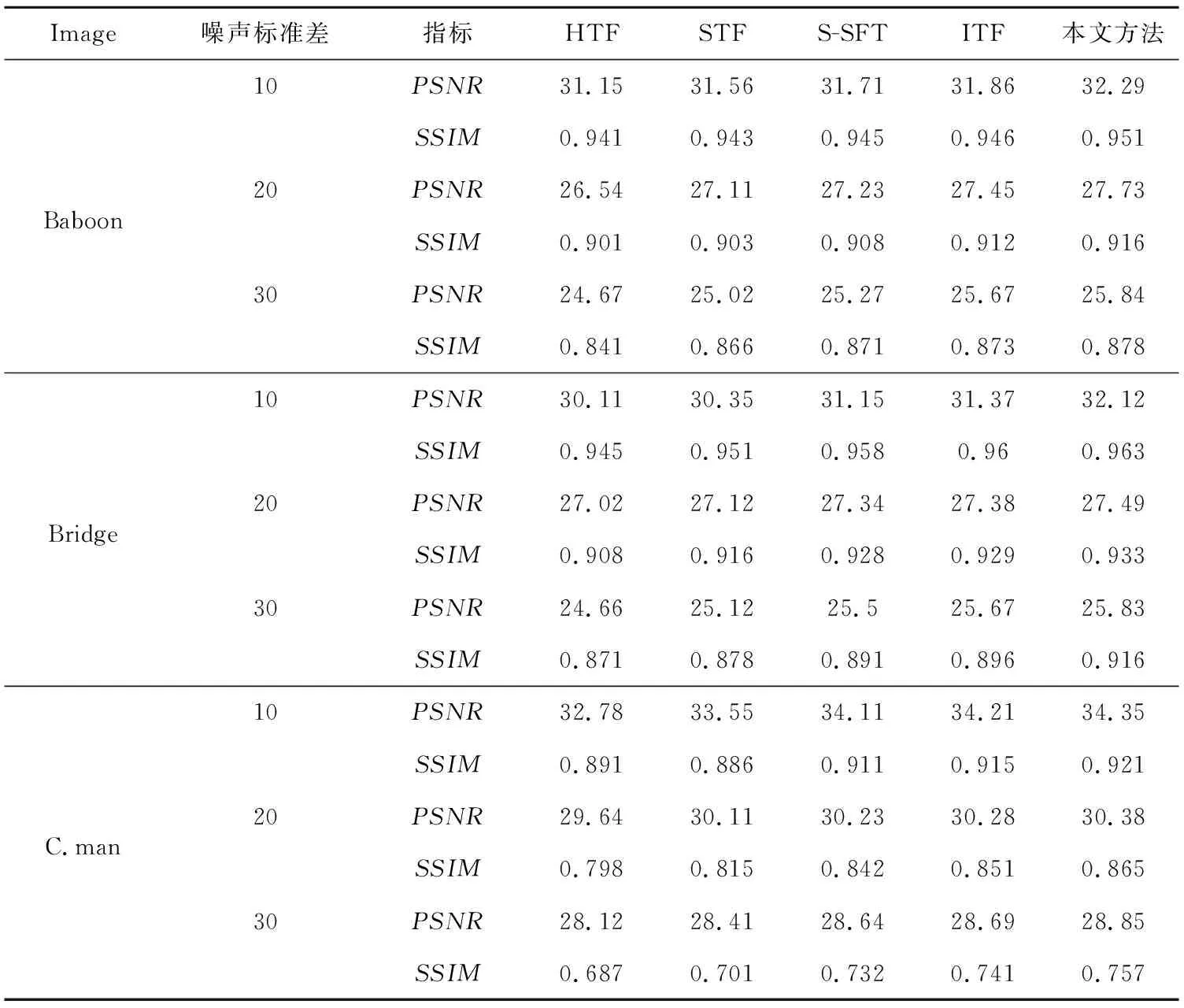
Table 2 PSNR and SSIM of denoising methods with different threshold functions

由表2可知，在不同噪声强度下，不同的阈值函数均能取得一定的去噪效果，相比较其他几种方法，本文方法的阈值函数取得了最高的PSNR值和SSIM值，且随着噪声强度的加大，所有方法的PSNR值和SSIM值均有不同程度的下降，不同方法的下降幅度不同，本文方法一直保持在一个相对较高的水平，本文方法的PSNR指标高出HTF，STF，S-STF，ITF的PSNR值分别为1.32，0.72，0.41，0.26；SSIM评价指标高出值分别为0.035，0.026，0.012，0.009，上述数值说明本文方法相比较其他方法具有更好的去噪效果。

为直观展示不同去噪方法的效果，在Jetplane图像的基础上添加噪声标准差为20的高斯白噪进行分析，然后采用上述5种阈值函数的小波变换方法进行去噪，结果如图8所示。

Figure 8 Test results of different denoising methods on Jetplane 图8 不同去噪方法对Jetplane测试结果

图8所示为原始无噪图像、含噪图像，以及不同去噪方法的结果图像，为进一步直观分析去噪效果，所有结果图像选择“机尾翼”部分进行放大显示，放大图像置于各图像的右上角。由图8可知，硬阈值函数去噪方法去噪之后，结果中依然存在部分噪声，局部放大图中出现“振铃”现象。软阈值函数去噪方法去噪之后，图像的边缘细节较模糊，“尾翼”中的数据编号“01568”已经很难识别判断。半软阈值函数去噪方法去噪结果相对硬阈值、软阈值方法更好，但是局部放大图中，数据编号边缘及轮廓相对模糊。文献[18]的改进阈值函数去噪方法结果相对较好，但是相对本文方法而言，其结果依然不够理想。本文方法结果最好，局部放大图中，细节纹理清晰，边缘轮廓容易识别判断。

为进一步对比分析不同去噪方法的差异性，在原始标准Parrot图像上添加噪声强度为40的高斯白噪声，采用5种去噪方法进行测试，然后将不同去噪方法的去噪残差进行对比。为直观展示残差结果，将原始图像、噪声图像以及残差图像转换为二值图像，在残差结果的二值图像中，白色像素表示去噪彻底，黑色像素表示去噪较差。不同方法处理前后的二值图像如图9所示。

Figure 9 Binary image of test results on Parrot 图9 Parrot测试结果的二值图像

由图9可知，对于图像的去噪结果，边缘/纹理等细节区域普遍存在较多的黑色区域，但是不同方法的黑色区域分布范围不同。在图9c和图9d中存在较多的黑色像素，表明硬阈值函数去噪方法和软阈值函数去噪方法去噪能力不足，或容易引入外来噪声使结果图像中出现“振铃”现象。相对硬阈值函数去噪方法和软阈值函数去噪方法处理结果，半软阈值函数去噪方法和文献[18]的改进阈值去噪方法结果的黑色像素相对较少，说明去噪结果较好，具体如图9e和图9f所示。本节方法的噪声残差图像中，黑色区域最少，说明本文方法的去噪效果最好。

3.4 新改进的小波软阈值函数方法在其他噪声类型下的应用

数字图像在实际的传输和压缩过程中，受环境条件的影响，容易在图像中添加不同类型的噪声，甚至一幅图像中存在多种类型的噪声，目前最为常见的噪声是脉冲噪声和高斯噪声。实际医学B超图像由于超声脉冲的干涉，图像含有较多的散斑脉冲噪声，该噪声的存在，使得图像中的人体结构及组织细节信息难以识别，边缘模糊，降低了图像质量，不利于后续医学治疗手段的开展。为进一步分析本文方法对于脉冲噪声的去除效果，本节继续采用3.3节所述5种方法对含有脉冲噪声的原始B超图像进行处理，去噪结果和去噪残差分别如图10和图11所示。

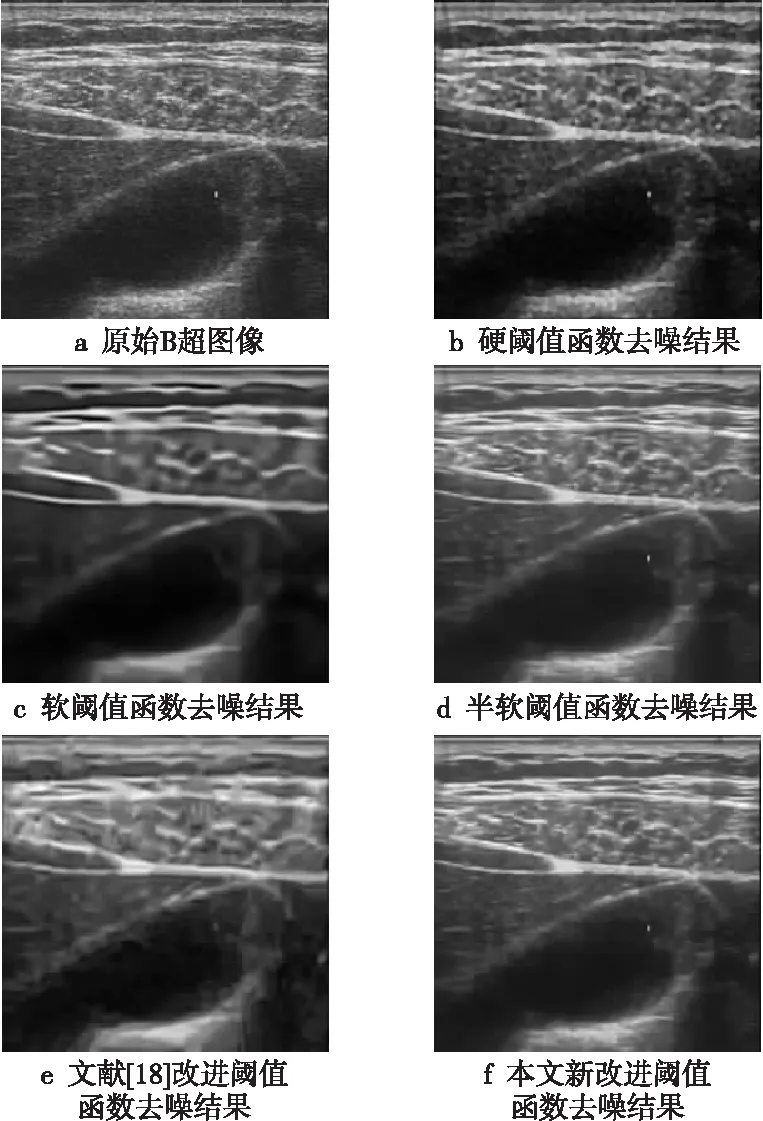
Figure 10 Test results of different denoising methods on B-ultrasound image图10 不同去噪方法的B超图像测试结果

Figure 11 Denoising residuals with different denoising methods on B-ultrasound image 图11 不同去噪方法的B超图像去噪残差

由图10和图11可知，5种方法均能提升B超图像质量，但是不同的去噪方法其结果有所差异。硬阈值函数去噪方法结果纹理细节较为模糊，其去噪残差中存在较多的连续结构信息，表明对图像的细节损伤较为严重；软阈值函数去噪方法结果相对较好，但是残差中依然存在一定的连续结构信息；半软阈值函数去噪方法的结果图像质量较好，但是残差中存有少量的连续纹理；文献[18]的改进阈值函数去噪方法去噪残差中存在大量的“大颗粒”斑状噪声，说明去噪过度；本文方法去噪结果中，几乎不含连续的纹理结构，去噪残差中的噪声颗粒分布均匀大小适中，表明去噪结果好，对纹理细节保护好。

常规的图像质量评价指标，例如前文采用的PSNR和SSIM，需参考原始无噪图像，然而实际B超图像几乎没有不含噪声的图像，因此常规方法很难评价实际B超图像的去噪效果。针对上述情况，本文采用图像均方根误差MSE(Mean Squared Error)和边缘保护指数EPI(Edge Preservation Index)对去噪结果进行评价，同时统计不同结果的专家评估值，其中MSE值越大，可以认为去噪能力越强；EPI值越大，表明边缘保护效果越好；专家评估值越大，说明图像质量越高，B超图像处理前后的评价值如表3所示。

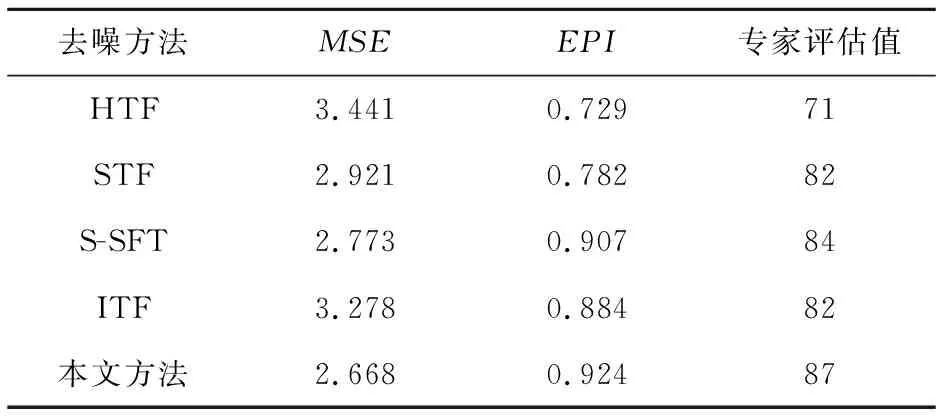
Table 3 Evaluation of denoising results on B-ultrasound image

由图10、图11和表3可知，小波硬阈值方法直接削减噪声小波系数，在去除噪声的同时容易损伤边缘信息；而软阈值对其他小波系数进行修正后对图像影响较大，因此MSE值高，但是也模糊了边缘，因此EPI值较低；半软阈值函数相对较好，但是边缘保持能力依然有待提升；文献[18]改进的阈值函数方法边缘保持较好，但是和原始图像差异性较大；本文方法在有效去噪的同时可以保护边缘信息，提升视觉效果，表明本文方法也具有较高的去噪能力。

4 结束语

在分析小波阈值去噪原理的基础上，对比分析不同阈值以及阈值函数的特征，提出一种改进软阈值函数方法，该方法在阈值公式中引入一个随小波分解层数变化的缩放参数，使得阈值能够随噪声模值变化，同时改进的阈值函数在阈值位置处更加连续更加稳定，改善了常规阈值函数在阈值位置处存在震荡现象的缺陷，使得去噪后的图像保真性更好。一系列实验结果表明，在调节参数最优时，本文方法的去噪效果明显好于常规阈值函数方法，图像边缘/纹理等细节清晰完整，表明本文方法在图像处理中具有较好的可推广性。