基于GPS-IR的归一化植被指数反演

肖星星，吕伟才，仲臣，曹进进，李延杰，张灿

（ 1. 安徽理工大学 空间信息与测绘工程学院, 安徽 淮南 232001；2. 安徽理工大学 矿区环境与灾害协同监测煤炭行业工程研究中心, 安徽 淮南 232001；3. 安徽理工大学 矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室, 安徽 淮南 232001；4. 安徽广航建设工程有限公司, 安徽 芜湖 241002 ）

0 引 言

归一化植被指数(NDVI)被用作对植物覆盖面积生长状况的长期监测，是衡量植被覆盖的标准化方法，对因植被覆盖变化导致的区域气候变化，农作物种植面积等研究提供定量的判断依据[1-2]. NDVI作为分析人员在遥感中最常用的指标，形成了改进型甚高分辨率辐射计(AVHRR)、中分辨率成像光谱仪(MODIS)、可见光红外成像辐射仪(VIIRS)等数据采集形式，但此类方法对观测条件要求较高，且背景噪声消除复杂，难以完成连续观测[3-4].

相较于上述方法， GPS对地观测不仅能克服NDVI数据采集的缺陷，而且具有大范围、全天时全天候、连续运行等先天优势. GPS是通过地面接收设备接收来自空间卫星发射的无线电信号，进行空间定位的空间导航系统，其中L波段微波信号有良好的大气穿透性，会被植被含水量的细微变化产生干涉，导致载波信号振幅的改变. 这一特性为使用GPS干涉反射测量(GPS-IR)进行NDVI反演提供了条件.LARSON等[5]利用GPS反射信号特点，对地表积雪厚度进行了测量，证明了GPS进行地表覆盖形态观测的可行性；CHEW等[6]同时对土壤湿度进行了反演，进一步说明了利用GPS反演土壤理化性质具有较高精度；SMALL等[7]也通过计算GPS伪距多路径均方根误差(RMSE)进行植被含水量的反演，证实了其与植被各阶段生长状况不同含水量存在较好的相关性；随后LARSON[8]等提出了一种归一化微波反射指数(NMRI)，发现在植被指数的反演过程中具有较好的实用性. WAN等[9]建立了GPS反射信号振幅与植被含水量之间的回归模型，发现反演出的植物含水量模型具有较高精度；郑南山等[4]将BP神经网络应用于NDVI模型反演中进一步提升模型精度. 上述研究成果为利用GPS反射信号来进行NDVI反演提供了理论依据.

综上，GPS-IR反演NDVI具有观测成本低廉、实时连续、不受传感器和大气环境限制等优点. 本文基于上述特点对两个不同区域GPS参考站数据进行实验研究，进行了NMRI与NDVI之间的相关性分析，实现了NDVI植被指数的反演.

1 原理与方法

1.1 GPS-IR进行NDVI反演原理

图1为GPS接收机在对地观测中记录的信号强度变化. 其中L波段有较好地大气穿透性并且对于植被水分含量变化比较敏感，因此GPS接收机接收到L波段的直射信号，与地面植被反射信号产生干涉.

图1 GPS-IR进行NDVI反演几何模型

由于多路径效应导致接收到的反射信号振幅发生变化，对振幅进行处理计算归一化微波指数. 其中GPS-IR可以采用常规单天线测量型接收机进行地基观测. 地面上有效观测反射区是指接收机能够接受到反射信号区域，在测区较为平坦的条件下，此区域可以用第一菲涅耳反射区进行较为全面的描述.

如图2所示，Q点为空间卫星在地面的镜像点，由惠更斯-菲涅尔原理[10]可知，以Q点和接收机为焦点的旋转椭球面中空间区域为菲涅尔反射区，此椭圆与地面相交区域(图2中黄色区域)即地面反射的有效区域为第一菲涅耳反射区，由长半轴a、短半轴b决定的椭圆，其长、短半轴可根据下式计算：

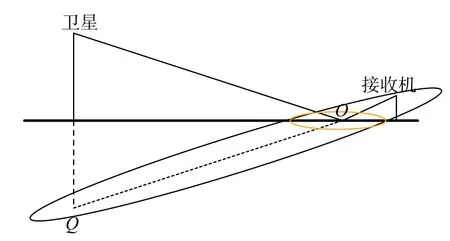
图2 菲涅尔区示意图

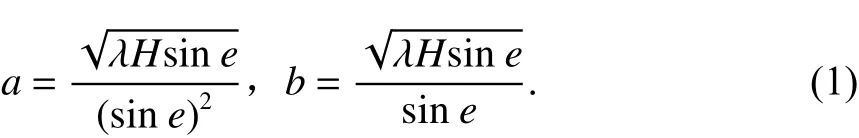
式中： λ 为GPS卫星载波波长，单位为m；H为接收机天线高，单位为m；e为卫星高度角.

由式(1)可知，当GPS观测条件作为固有变量保持不变时，第一菲涅尔反射区形状影响参数仅为卫星高度角，当使用载波波长为0.19 m的L1载波信号作为计算参数时，接收机天线架设保持1.8 m高度不变时，以自变量高度角5°，有效反射区域为141.443 8 m2；当高度角选择7°时，有效观测面积缩小至72.341 4 m2；卫星高度角为10°，有效观测面积为35.631 6 m2.为了方便观察上述性质，选用卫星方位角为0°进行绘图，图2中接收机位置为(0，0)点天线高为1.8 m.

由图3可知，接收机天线架设稳定后卫星高度角越大，反射信号覆盖区越小，且逐渐向接收机方向缩小[11-13].

图3 不同高度角下的有效散射区大小

反射点位置是在接收反射信号的过程中，其反射信号与接收信号的最短路径与反射面的交点，其中该最短路径称为径向距离. 如图1所示，反射信号在地面的反射点O为反射点位置，由接收机天线高和卫星高度角定义

式中：r为径向距离，单位为m；H为接收机天线高；e为卫星高度角. 随着GPS卫星与接收机相对位置的变化，反射点轨迹也随之变化，在不同的弧度表现出不同的走向和分布情况. 图4给出了径向距离与卫星高度角、接收机天线高度的关系图.

图4 径向距离与卫星高度角、天线高度的关系图

由图4可知，随着GPS卫星与接收机相对位置的变化，反射点轨迹也随之变化，在不同的弧度表现出不同的走向和分布情况. 径向距离与卫星高度角的变化成正相关，与天线高度成负相关. 综合多颗卫星反射点轨迹和菲涅尔反射区计算，可判定反射信号充分携带参考站周围的植被信息，所以准确确定菲涅尔反射区，直接关系到NDVI遥感的准确性和精度.

1.2 NMRI

NMRI是衡量GPS反射信号振幅变化的一项重要指标，其中对于L1载波上伪距多路径RMSE用MP1的计算可表示为[14]

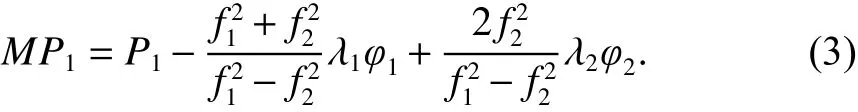
式中：P1是以m为单位在L1载波上伪距观测值；f1=1 575.42 MHz，f2=1 227.60 MHz；λ1=0.19 m，λ2=0.24 m；

φ1和φ2是以周为单位的L1、L2载波相位观测值. 首先对接收机观测数据进行去均值化处理并整合，获得全部MP1的 RMSE 数值；然后基于卫星寻优进行分类加权平均处理，以此得到更为准确的MP1的 RMSE数值. NMRI的计算方法为

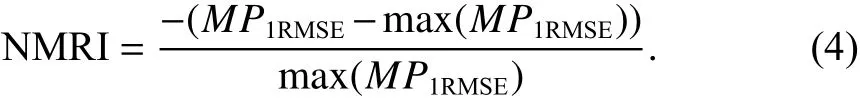
式中：MP1RMSE是单日MP1的RMSE值；max(MP1RMSE)是将MP1RMSE序列数值进行由大到小排列后前5%的MP1RMSE的平均值，其结果均在0～1，不排除少数负值出现的可能. 与NDV1保持一致.

1.3 NDVI

NDVI是通过近红外波段和红光波段二者反射率的差值与和值进行作比产生的用于反映地面绿色植被量的测度. 其计算公式为

式中， ρch2和 ρch1分别表示近红外波段和红光波段经过误差校正后的地面反射率. 红光波段是植物将入射辐射吸收的波段，近红外波段是植物将入射辐射强烈反射波段. NDVI的取值范围是[-1，1]，负值部分表示观测区域内存在对可见光高反射性地物，如湖泊、冰雪层等，0的出现表示土地岩石直接裸露，正值部分数值越大表示地面绿色植被覆盖率越高.

2 实验与分析

2.1 数据来源

本次用于实验的数据来自美国大陆板块观测网(PBO)中P041站点2012—2016 年和P049站点2008—2012 年的GPS观测数据，站点位于美国中西部草原地区，站点周围地势平坦，无大型障碍物遮挡和人为活动因素干扰，利于GPS数据信息采集. 且站点周围的植被有明显的年际变化和物候特征，参考站的观测环境如图5所示.

图5 GNSS 参考站

为保证实验条件的一致性，选择使用相同接收机和天线的参考站进行数据采集，其中P041和P049使用接收机和天线型号分别为TRIMBLE NETRS和TRM29659.00，观测姿态为天线指向天顶(U)方向，采样间隔设置为15 s. 参考站概略信息如表1 所示.

表1 GPS 参考站概况 (°)

本文NDVI数据来源于美国地质调查局陆地过程分布式数据档案中心，由于MODIS 产品数据MOD13Q1准确度较高作为对比数据使用，此数据空间分辨率为250 m，时间分辨率为16 天.

2.2 数据处理

首先对测站GPS数据进行处理，经式(4)计算得出反射信号的归一化微波指数NMRI，得出的2个参考站的NMRI时间序列绘制成图，如图6所示.

由图6可知，2个站点的NMRI呈现明显的周期性且数据波峰和波谷出现时间相似，这与植被生长随季节性变化表现出相同的特性. 同时2个站点均存在明显的粗差点，这是由于GPS参考站在观测过程中易受到降雨、降雪等天气影响，导致观测值与实际值产生偏差. 为削弱这种偏差，通过参照GPS气象文件进行手动剔除降雨时间段观测数据；为减少离群噪声点影响，将观测值与平均值之差的数据中大于2倍中误差的观测数据剔除，其结果如图7所示.

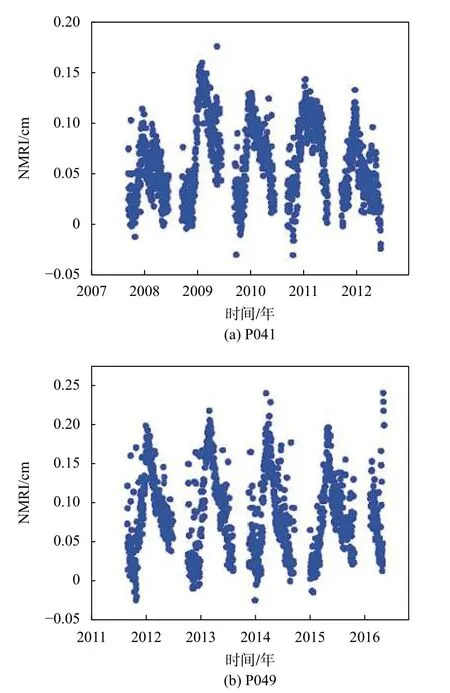
图6 参考站 NMRI

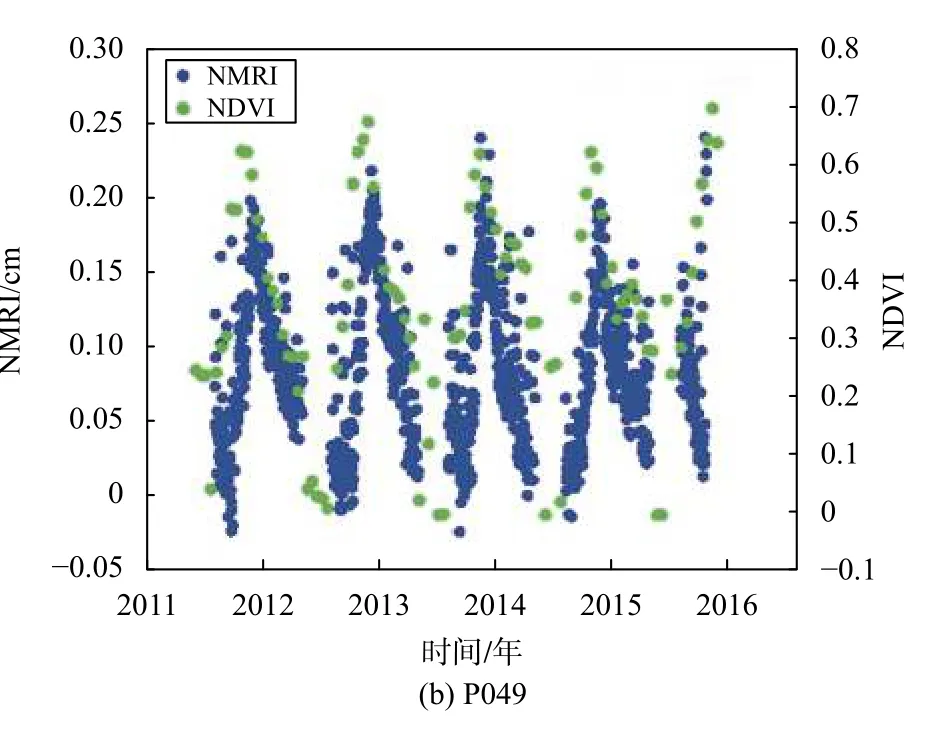
图7 剔除粗差后的NMRI（蓝色）与NDVI（绿色）

与图4对比可知，NMRI由于环境因素引起的误差离群点明显减少，NDVI散点图均出现在NMRI数据周围且波峰和波谷出现时间吻合度较高，因此两变量在时间上具有相似的周期规律. 由上述结果可初步判断NMRI与NDVI间存在相关性，为实现NMRI反演NDVI增加了可能性，进而进行模型验证实验.

2.3 模型验证

为验证该理论，选取80%的实验数据在 NMRI与 NDVI间分别建立一元线性回归模型和BP神经网络反演模型，并使用剩余数据进行模型验证. 回归分析结果如表2所示，建模结果如图8所示.

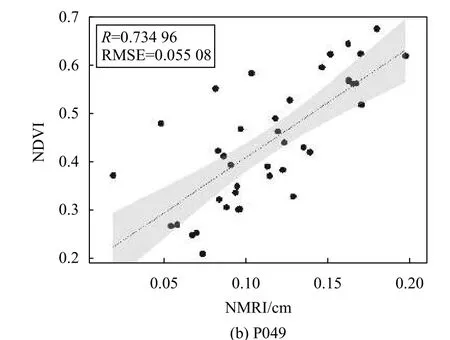
图8 建模结果

表2 回归分析结果

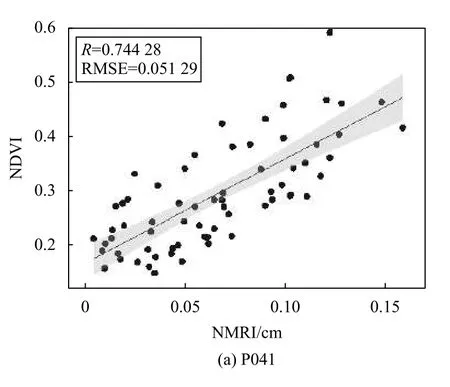
相关研究表明，来自数据量和参考站观测系统处理反射信号的方式不同，因此P041和P049两测站回归系数不同，且接收机类型甚至固件的版本都会引起MP1RMSE数值的发生尺度变化[15-16]. 两站点数据通过建立一元线性回归模型得到的相关系数分别是0.744 28和0.734 96. 在显著性检验中，显著性水平选择0.05时，T检验全部满足精度要求. 在模型验证中，通过表2所示线性回归模型将实验预留剩余NMRI时序数据进行拟合得出相应的NDVI值，再将遥感卫星计算获取的NDVI值作为地面验证的真实值使用，最终获得每站NDVI的反演结果的RMSE分别为0.051 29、0.055 08.

为进一步提高反演效果，引入3-8-1(三个输入层八个隐藏层一个输出层)的拓扑结构BP神经网络模型. 如图9所示，增加植被背景湿度信息作为一个输入项与NDVI、NMRI共同组成三个输入层. 采用八个隐藏层，主要负责通过激活函数进行信息处理与变换，后传向输出层各神经元；最后将NDVI数值作为输出层.

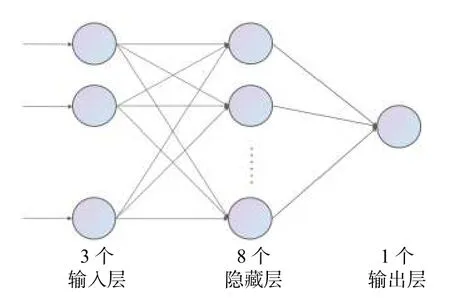
图9 三层 BP神经网络结构图

其中实验数据与上述数据分配一致，将该实验结果与一元线性回归模型对比得到P041和P049站点的相关系数分别提升2%和6%，RMSE分别为0.049 2和0.054 01，提升了反演的准确性.

最后将NDVI 反演结果的相对误差区间分布规律进行统计分析，图10为绘制的反演NDVI模型检验的相对误差概率统计图.

由图10可知，经过模型预测的NDVI相对误差值峰值部分均落在-0.1～0.1，精度较高；统计得出测站的反演相对误差落在±0.2区间内的数据量占比均达到70%以上，相对误差集中于0附近，伴随着相对误差增大后，其所占比例越来越小，图中显示误差分布总体上接近于正态分布，证明建立的NMRI反演归一化植被指数模型是有实际意义的.

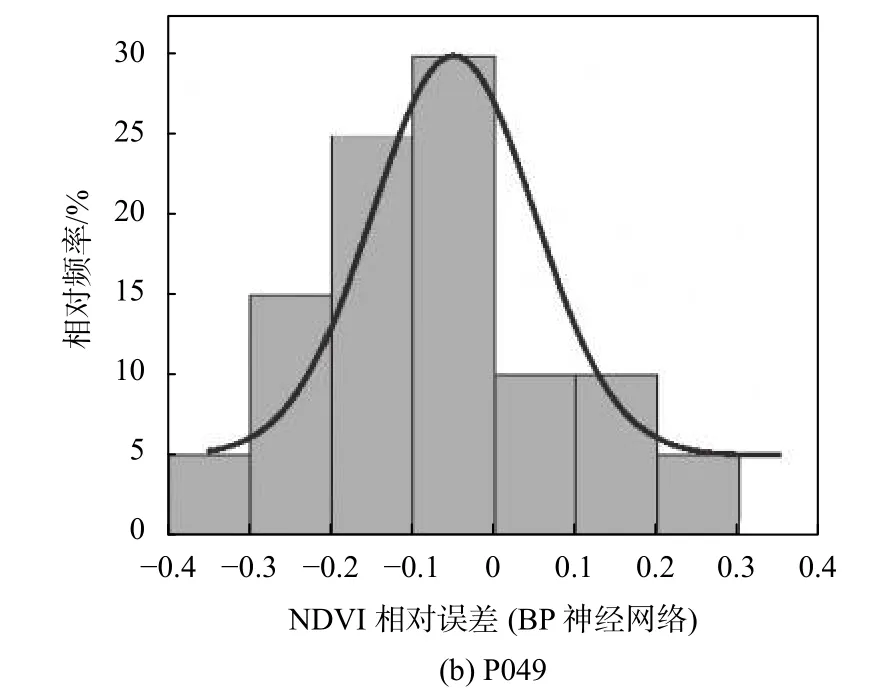
图10 模型检验的误差统计

3 总 结

为克服AVHRR、MODIS等遥感数据产品存在的土壤湿度噪声、观测成本高及不易获取高时间分辨率归一化植被指数等缺陷，本文利用GPS-IR作为遥感信息源进行NDVI反演，通过对大量连续时序实测数据进行分析，结果表明：

1) GPS多路径数据产生的NMRI与NDVI时序数据具有相同的起伏形态且与实际气候周期相关联.

2) 测区及周围进入雨水充足的季节时，植被量和水分含量增长，反射信号振幅减小，NMRI增大. 同时雨雪天气易产生的噪声点容易分辨剔除.

3) NMRI 与 NDVI 在统计数据内具有一定的相关性，在此基础上建立反演NDVI的一元性回归模型，相关系数分别是0.744 28、0.734 96，经过模型验证反演出NDVI 相对误差的RMSE为0.051 29、0.055 08；同时引入BP神经网络模型，进一步提高反演相关性. 因此通过GPS-IR技术进行NDVI反演结果具有可靠性和准确性.

文中为减少复杂高矮植被、湖泊等外部环境因素影响，选择开阔草地的测站点数据采集并进行NDVI反演. 对于复杂环境反演效果及有效散射区进行计算等问题还需在后续进一步深入研究. 此研究结果为区域性NDVI数据采集提供了新的方式和思路.