基于微分对策的鲁棒导弹自动驾驶仪设计

陈必露， 刘春生， 袁斐然

(南京航空航天大学，南京 211000)

0 引言

导弹作为一种精确制导武器，在现代化战争中意义重大，其制导控制系统由制导和控制两部分组成，其中，控制部分主要体现在自动驾驶仪的设计。随着现代战场呈现出的高度信息化、复杂化特征，导弹控制系统的稳定性和鲁棒性亟待提高。因此，相应的现代控制理论和先进控制方法也被应用于导弹自动驾驶仪的设计。文献[1]针对导弹自动驾驶仪的纵向动力学问题，在设计非线性干扰观测器(NDO)观测部分未知干扰的基础上，结合滑模控制(SMC)理论提出了不依赖于干扰上界的自适应反馈控制方法并进行自动驾驶仪设计，从而提高了系统的鲁棒性；文献[2]针对BTT导弹的抗干扰自动驾驶仪问题，设计了一种抗尖峰滑模控制器，有效抑制了高观测增益造成的系统性能下降现象。

此外，随着导弹的智能化发展需求，其控制过程中的一些最优特性(如最小耗能等)也值得考虑。但是，导弹等非线性系统的控制问题需要求解复杂的非线性偏微分方程，一般的解析方法在进行求解时会陷入“维数灾难”现象。为解决该问题，自适应动态规划(ADP)算法被提出,并成为非线性最优控制领域的研究热点[3-4]。文献[5]针对导弹自动驾驶仪的纵向动力学控制问题，通过结合NDO,SMC和最优控制方法，基于ADP算法实现了系统状态受限下的鲁棒最优控制，有效抑制了非匹配干扰带来的不利影响。

微分对策作为控制论的重要分支，是处理双方最优控制的理论。本文受文献[6-7]启发，设计了一种复合控制方案。首先利用超螺旋干扰观测器(STDO)观测匹配输入干扰,并结合积分滑模控制器(ISMC)方法设计滑模控制器补偿匹配输入干扰；其次，将自动驾驶仪的控制输入和外界非匹配干扰看作是博弈双方，基于ADP算法求解出微分对策控制器；最后，仿真表明，所设计的复合控制方案有效提高了导弹纵向动力学系统的鲁棒性。

1 问题描述

考虑一类受时变干扰影响的连续时间仿射非线性系统

(1)

式中：x∈Rn，为系统状态;u∈Rm,为控制输入;ud∈Rm,d∈Rk，分别表示匹配干扰和非匹配干扰;f(x),g(x)和k(x)为连续可微的系统矩阵，假定f(x)+g(x)u是Lipchitz连续,且f(0)=0。

为了便于下文观测器和控制器设计，做如下假设[8]。

假设1f(·),g(·)和k(·)为已知连续有界函数。

针对式(1)系统，目标为设计一种复合鲁棒控制方案来补偿干扰对系统的不利影响，同时保证系统状态最终一致有界(UUB)稳定。其中，复合控制器由两部分组成，即

u=us+ua

(2)

式中:滑模控制器us通过选取STDO获得对输入干扰的估计，并结合积分滑模控制方法进行设计以补偿干扰ud；自适应控制器ua针对干扰补偿后的标称系统，利用微分对策理论和ADP算法设计来补偿非匹配干扰d。

2 复合控制器设计

2.1 基于STDO的滑模控制器设计

首先，设计STDO为

(3)

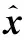
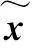
根据设计的观测器式(3),为消除输入干扰对系统的影响，结合滑模控制方法，设计滑模面

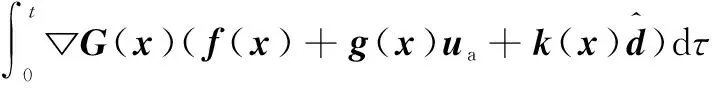
(4)

式中:G(x)∈Rm,为积分滑模控制中设计的矩阵向量；▽G(x)=∂G(x)/∂x，为其关于状态x的偏导数。

针对滑模面式(4),设计自适应滑模控制律为

(5)

式中，c为可调增益。

定理1针对系统式(1),设计STDO式(3)观测输入干扰ud，分别设计滑模面式(4)和滑模控制器式(5),则系统的状态量将收敛并维持在滑模面上。

证明 取Lyapunov函数Ls(t)=0.5STS，求导

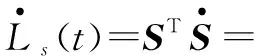
(6)

因此，根据Lyapunov稳定性理论，系统状态将收敛并维持在S=0，即滑模面上。

本节结合滑模控制理论，设计自适应滑模控制器对匹配干扰进行了补偿，将对原式(1)系统的控制问题转化为标称系统的最优控制问题。

2.2 基于ADP算法的微分对策最优控制器设计

考虑标称系统

(7)

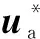
对于系统式(7),定义性能指标函数为

(8)

式中:Q1为半正定矩阵;R1和R2均为正定矩阵。

定义系统式(7)的哈密顿(Hamilton)函数为

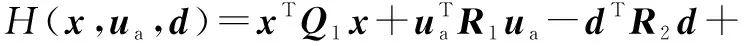
(9)

式中，▽J(x)=∂J(x)/∂x。

根据Hamilton-Jacobi-Isaacs(HJI)理论，最优性能指标函数▽J*(x)满足

(10)

假设式(10)的解存在且唯一，则系统式(7)的最优策略满足∂H(·)/∂u=0,∂H(·)/∂d=0，解得

(11)

由式(10)和式(11)发现，获得最优控制策略需要求解HJI方程，而此非线性偏微分方程很难用解析方法求解。因此，将结合ADP算法求解该HJI方程并设计最优控制器。

在设计控制器之前，基于文献[10]做如下假设。

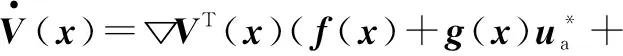
(12)

成立。采用单评价神经网络结构逼近最优性能指标函数及其梯度分别为

(13)

式中:WJ∈Rl，为理想权值向量；φJ(x)∈Rl，为激励函数；l表示评价网络中的神经元个数;εJ(x)表示神经网络的逼近误差。

将式(11)和式(13)代入式(10)得到

(14)

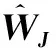
(15)

通过式(11)和式(15)，近似最优控制策略为

(16)

将式(16)代入式(10)，得近似Hamilton函数为

(17)

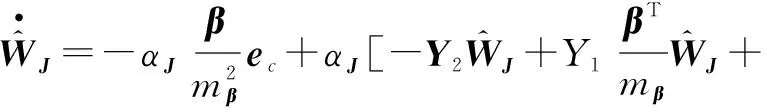
(18)

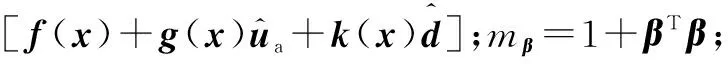
(19)

根据设计的最优控制策略式(16)和权值更新律式(18),在稳定性分析之前，给出如下假设与定理。

假设4 评价网络的理想权值与逼近误差εJ(x)的偏导数▽εJ(x)均有界，界值分别满足‖WJ‖≤bW，‖▽εJ(x)‖≤bε，bW和bε为大于零的常数。

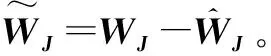
证明 结合Lyapunov稳定性理论，选取Lyapunov函数

(20)

对式(20)求导，可得

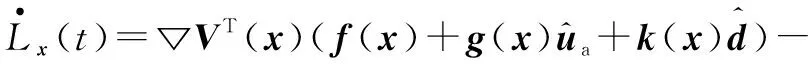
(21)

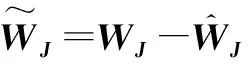
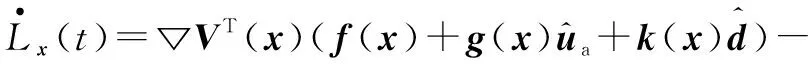
(22)

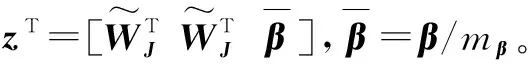
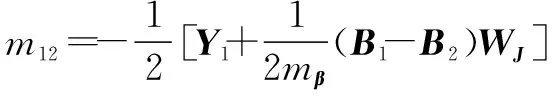
泡沫混凝土应符合《泡沫混凝土》［4］的标准要求，28 d抗压强度不小于2.0 MPa；所使用的外加剂（水泥强度激发剂、减水剂和发泡剂等）亦应满足规范要求。

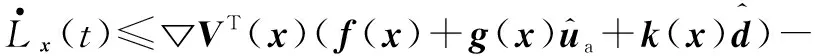
(23)

式中，λ表示M矩阵的最小特征值。

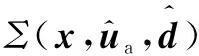
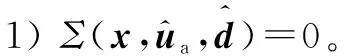
(24)

此时，只要不等式

(25)

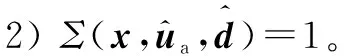
(26)

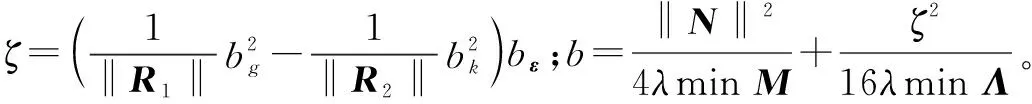
(27)

或者

(28)

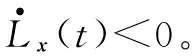
考虑以上两种情况，结合Lyapunov稳定性理论可知定理2成立。

3 导弹自动驾驶仪设计

基于上述复合控制方案，选取导弹自动驾驶仪的纵向动力学方程

(29)

式中:xT=[αqδ]，α，q和δ分别表示导弹的攻角、俯仰角和尾翼偏转角;d表示由建模误差或外部风力等因素产生的扰动项；f1(α)，f2(α)，b1和b2是由气动系数决定的非线性函数；t1表示尾翼执行器的时间常数。不失一般性，上述函数满足[5]

(30)

式中:η1=180gQs/πmv，η2=1.03×10-4，η3=9.45×10-3;η4=180QDs/πIyy,η5=2.15×10-4，η6=1.95×10-2。假设输入干扰ud为

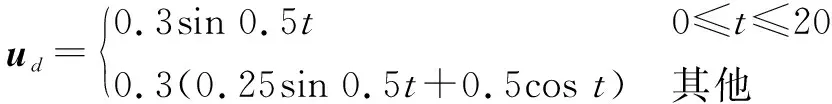
(31)

此外，各项参数为:导弹的质量m=4410 kg，速度v=947.6 m/s,俯仰惯性矩Iyy=247.44 kg·m2,导弹所受动压Q=293.638 N/m2，其参考面积为s=0.040 87 m2，参考直径D=0.229 m，尾翼执行器的时间常数t1=0.1 s，重力加速度g=9.8 m/s2。

根据自动驾驶仪模型式(30),选取各项参数如下。

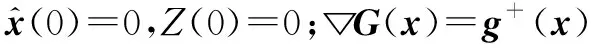
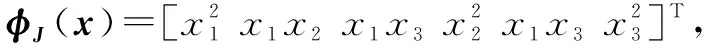
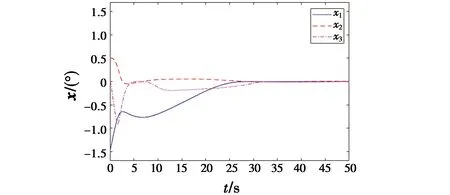
图1 系统状态x的轨迹Fig.1 The trajectories of system state x

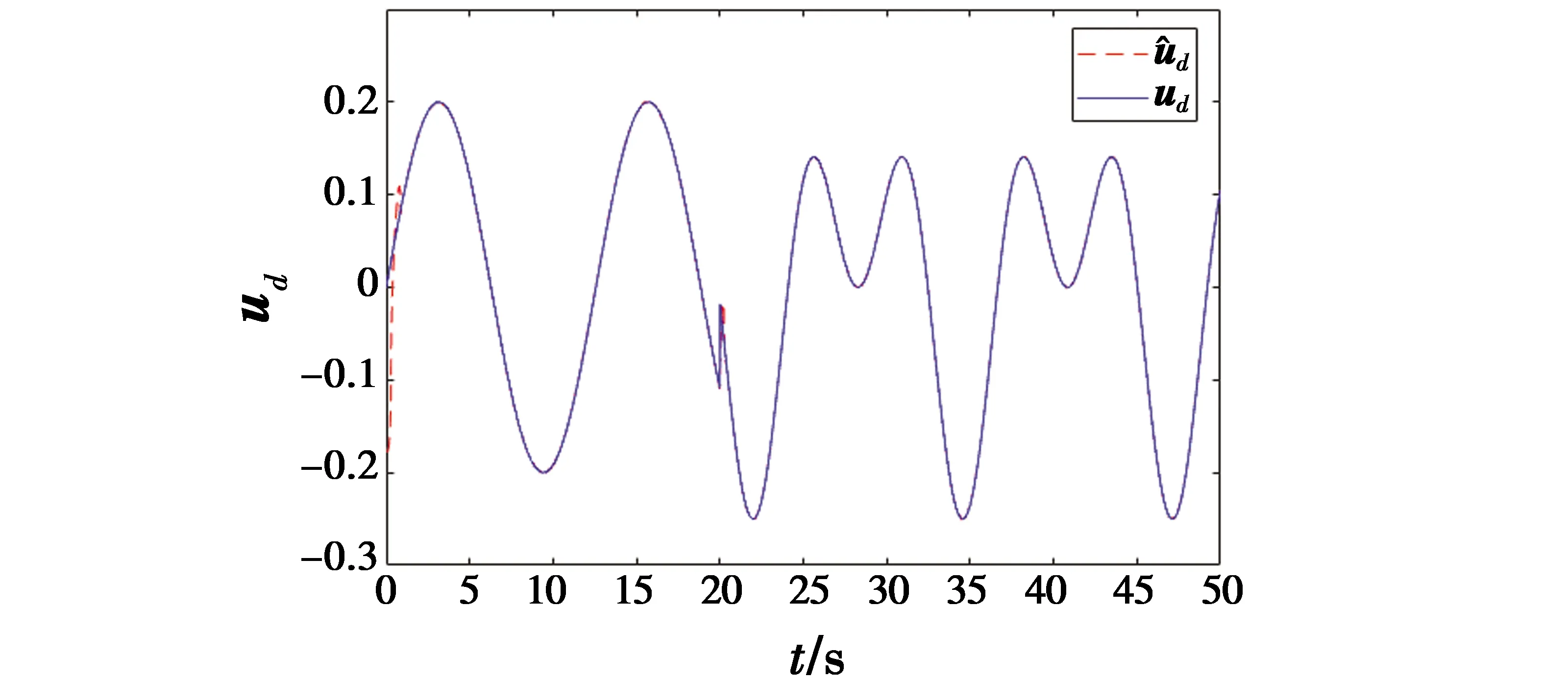
图2 STDO实现干扰ud估计Fig.2 Estimation of udby STDO

图3 评价神经网络的权值Fig.3 Weights of critic NN

从图2可以看出，设计的STDO在经过一段时间后实现了对输入干扰的可靠估计；图3反映了评价网络的输出最终收敛至理想权值；图4为基于上述有效信息得到的复合控制输入;结合该复合控制，系统状态逐渐收敛并稳定，如图1所示。

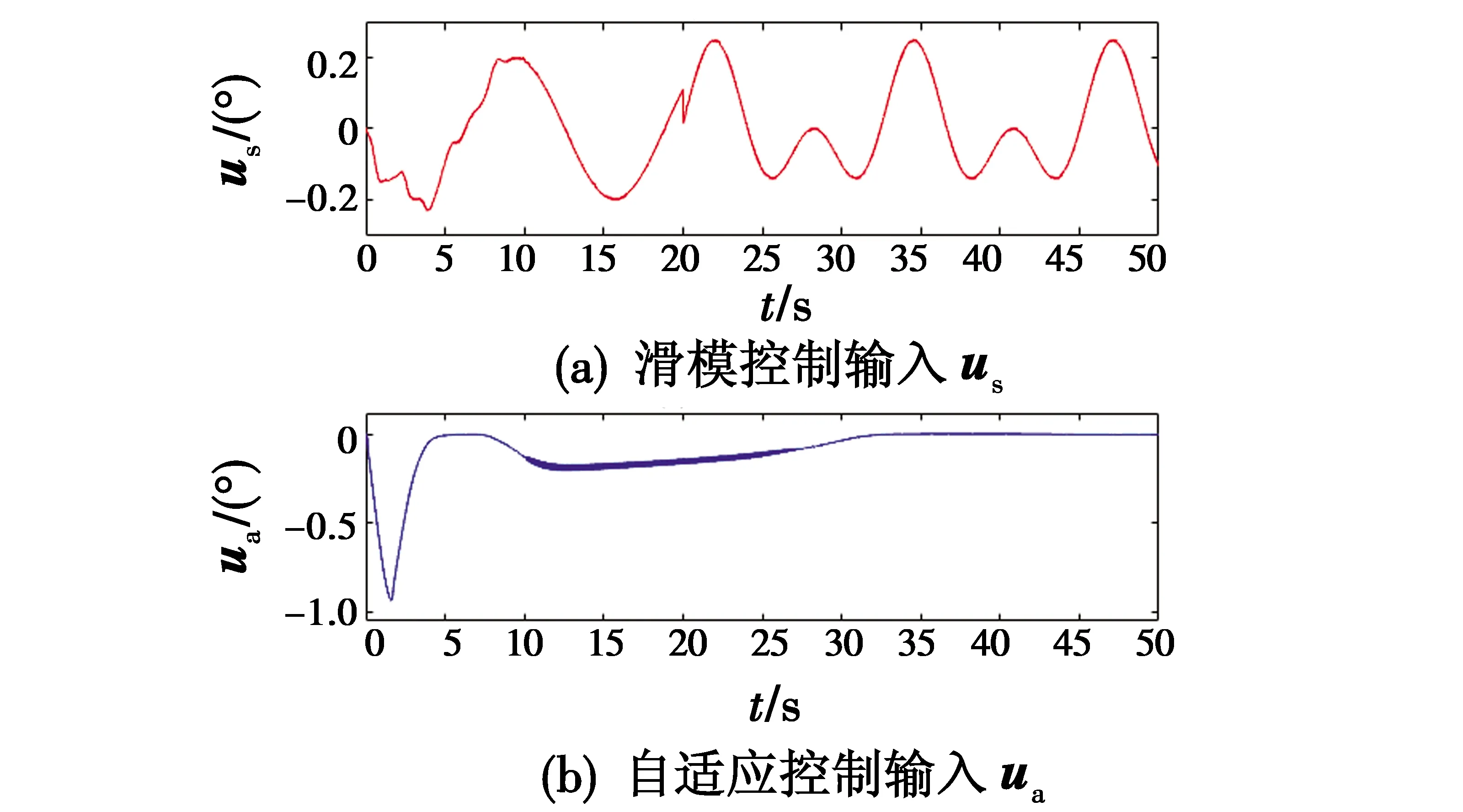
图4 复合控制策略Fig.4 Composite control strategies

其次，为验证提出的微分对策控制律对一般干扰的鲁棒性，选取非匹配干扰为d1，即

(32)

调整参数Y2=10.5I6，Y1=200·[111111]T，系统式(30)的初始状态满足x0=[-1-1.6-0.5]T，其他参数不变，得到图5和图6所示系统的动态响应和权值变化曲线。

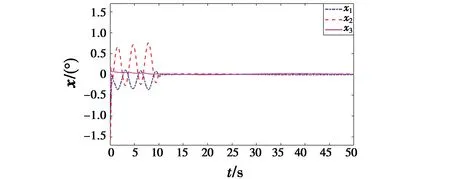
图5 d=d1时系统状态x的轨迹Fig.5 Trajectories of system state x when d=d1

图6 d=d1时评价神经网络的权值Fig.6 Weights of critic NN when d=d1

由图6可知，评价网络输出由于非匹配干扰的改变，在前期的学习过程中波动较大，但是当t=10 s后迅速收敛至理想权值；图5表明自动驾驶仪系统状态最终收敛至稳定状态。因此，仿真结果表明，上述提出的复合控制策略是有效的。

4 结束语

本文针对导弹自动驾驶仪的抗干扰问题，提出了一种滑模微分对策控制策略，构造了超螺旋干扰观测器(STDO)，并将其用于滑模控制律(SMC)的设计来抑制输入干扰带来的不利影响；同时，为了处理非匹配干扰，结合微分对策理论和ADP算法在线求解并获得了近似最优控制器以实现对该干扰的补偿，进一步增强了系统的鲁棒性。通过Lyapunov稳定性理论证明了闭环系统的稳定性。最后，仿真验证了本文所提算法的有效性，对处理一类非线性系统的抗干扰最优控制器设计有良好的参考价值。