基于图优化的INS/GNSS深组合导航系统研究

刘 娣， 刘 坤， 毕云蕊， 许有熊， 朱松青

(南京工程学院，南京 211000)

0 引言

从20世纪90年代以来，全球卫星导航系统(GNSS)得到了迅猛的发展，智能手机、无人驾驶汽车等都离不开卫星导航提供高精度的定位信息。通过接收卫星发出的信号，接收机可以实时计算自身的位置、速度和时间信息[1-3]。然而，由于周围环境的遮挡或者干扰，卫星导航信号十分脆弱，导致卫星导航接收机在信号较差的环境下定位精度很差，甚至无法提供导航信息。惯性导航系统(INS)依靠敏感的加速度和角速率信息来计算自身的位置、速度和姿态信息，不需要接收外界信息，具有很强的抗干扰能力[4]。但是，由于惯性器件的误差，惯性导航系统的定位误差随着时间发散[5]。卫星导航系统和惯性导航系统具有很好的互补性，通常通过卡尔曼滤波融合两者，输出高精度导航和定位信息。当卫星导航信号良好时，可以通过卫星导航的高精度定位信息对惯性导航系统误差进行估计和补偿；当卫星导航信号较差时，可以依靠惯性导航系统提供高精度导航和定位信息。根据信息融合层次，通常将INS/GNSS组合导航系统分为松组合、紧组合和深组合导航系统，其中，深组合导航利用惯性信息辅助卫星信号跟踪，可以提高组合导航系统抗干扰能力和复杂环境下的定位性能[6-7]。

INS/GNSS深组合导航系统是研究的热点，基于矢量跟踪技术的深组合导航系统得到了广泛的关注。矢量跟踪技术将导航信号反馈回信号跟踪环路，能有效提高信号跟踪能力。基于矢量跟踪的深组合导航系统采用组合导航系统信息反馈回跟踪环路计算信号跟踪参数，同时，跟踪环路产生的信号跟踪结果作为组合导航滤波器的量测信息，从而构成了INS/GNSS深度融合导航。ZHAO等[7]基于Matlab搭建了深组合导航系统并进行了代码开源，同时对深组合导航系统的实现细节和参数设置进行了描述； JIANG等[8]提出一种分布式深组合导航方法，减少了系统的计算量； NIU等[9]分析了IMU的不同误差项对深组合性能的影响，建立了相关的模型；KIESEL等[10]对深组合导航系统在高动态下性能进行了分析。目前深组合导航系统得到了广泛的研究，但是组合滤波器几乎都采用卡尔曼滤波。实际上卡尔曼滤波忽略了历史信息，在深组合导航系统中，状态之间是相互联系的，具体来讲，当前的导航估计结果会对下一时刻的导航结果产生影响。为考虑历史信息对当前定位精度的影响，基于图优化的分析方法得到了研究和关注，文献[11]研究了一种基于因子图的组合导航方法，并对其可行性进行了分析；文献[12]在利用EKF算法实现融合定位的基础上，提出了一种将EKF与图优化结合的融合定位方法；相关研究表明，基于图优化的算法能保证导航系统正常工作且满足定位精度要求，但现有研究均是基于惯性/卫星松组合导航系统进行的，未能对深组合系统进行分析，松组合导航系统仅单独使用卫星导航和惯性导航系统输出的位置和速度信息，没有充分挖掘两个系统的信息融合，因此有必要对深组合导航系统的图优化算法进行分析。

鉴于此，本文在充分考虑历史信息和导航系统深层次信息融合对定位精度影响的基础上，研究了一种基于图优化的INS/GNSS深组合导航方法，采用图优化算法取代卡尔曼滤波来完成信息融合，将INS/GNSS深组合导航滤波器的状态转移模型和量测信息作为约束，构建考虑历史信息的代价函数；在时间尺度上对状态进行优化估计，通过列文伯格-马夸尔特(Levenberg-Marquardt,LM)法求解状态的最优估计；最后，选择GPS卫星导航系统，通过仿真实验对本文提出的方法进行了评估和分析。

1 INS/GNSS深组合导航模型

本文构建的INS/GNSS深组合导航系统原理如图1所示。

图1 深组合导航系统原理图Fig.1 Schematic diagram of deep integrated navigation system

矢量跟踪环路的载波鉴别器/码鉴别器输出对应伪距率和伪距误差，作为组合导航滤波器的量测信息。通过组合导航滤波器估计惯性导航系统误差和本地时钟误差，将补偿后的高精度定位信息和时钟误差反馈回跟踪环路，计算信号跟踪参数，完成信号跟踪，同时产生新的量测信息进行下一次循环。通过这样闭环设计，本质上将惯性器件误差和卫星导航信号跟踪结果联系起来，构建起映射关系，通过载波/码跟踪结果来观测惯性器件误差，并通过组合导航滤波器估计惯性器件误差。

1.1 状态方程

深组合导航系统中组合导航滤波器状态向量包括惯性导航系统误差量和卫星导航时钟误差，具体为

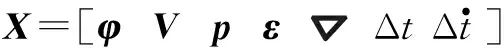
(1)

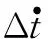
状态转移方程为

Xk+1=F·Xk+G·W

(2)

式中：F为17×17阶的系统状态转移矩阵；G为17×10阶的系统噪声驱动阵；W为噪声构成的10维向量。

1.2 量测方程

采用载波鉴别器输出和码鉴别器输出构建深组合导航系统量测方程，载波鉴别器输出和码鉴别器输出经过单位转换后对应于伪距率和伪距误差。假设有N颗卫星(即N个通道)参与定位，系统伪距观测方程为

Zρ=HρX+Vρ=[0N×6Hρ10N×6Hρ2]·X+Vρ

(3)

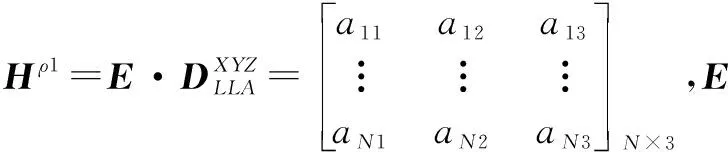
系统伪距率观测方程为

(4)

(5)

1.3 卡尔曼滤波

一般情况下，卡尔曼滤波包含状态预测和更新两个步骤，具体为

(6)

在量测更新步骤中，通过量测的更新来校正预测的状态向量和参数，更新状态向量，方程式为

(7)

时间更新和量测更新过程如图2所示。

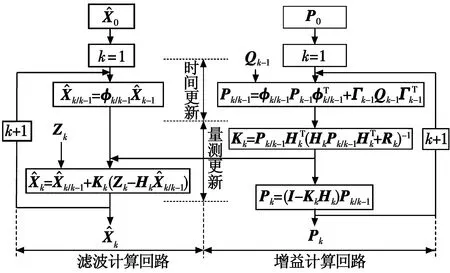
图2 卡尔曼滤波的时间更新和量测更新过程Fig.2 Time updating and measurement updating process of Kalman filter

2 图优化模型

卡尔曼滤波基于状态和量测模型以递推的方式估计和更新状态，默认当前状态只与前一时刻状态有关。实际上，历史状态会对后面的状态估计产生影响，而卡尔曼滤波忽略了这一点，充分利用过去历史信息可以提高当前状态估计的精度。本文采用图优化算法代替卡尔曼滤波器，构建基于图优化的组合导航方法。首先构建图优化算法的代价函数；然后给出一种基于列文伯格-马夸尔特法的最优状态求取方法；最后给出图优化算法在深组合导航系统中的实现过程。

2.1 图优化模型代价函数构建

根据深组合导航系统状态方程和量测方程，分别将状态方程和量测方程误差表示为

Estate，k=Xk-Φk,k-1·Xk-1

(8)

Emea，k=Zk-Hk·Xk

(9)

式中，Estate，k和Emea，k分别表示状态误差和量测误差，最优状态的估计可以归结为求这两个误差的最小值。基于误差式(8)、式(9)构建优化代价函数为

(10)

式中：Q表示系统噪声协方差矩阵；R表示量测噪声协方差矩阵。

将历史误差和当前误差叠加在一起，构建如下代价函数

(11)

式中，K表示参与估计的状态向量数，将在时间维度上连续的K个状态向量一起优化估计，可以充分利用历史信息和相连状态之间的联系，获得更加平滑和鲁棒的结果。过去k时刻的状态向量都作为变量，理论上，所有状态的最优估计满足式(11)的值最小，而卡尔曼滤波满足式(10)的值最小。

2.2 列文伯格-马夸尔特法

式(11)给出了图优化的代价函数，状态的估计可以归结为求取该公式的最小值，本文采用列文伯格-马夸尔特法。假设代价函数为[13]

(12)

式中:Ek为误差；Ω为方差矩阵的逆矩阵。

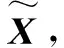
(13)

式中，Jk表示误差函数在初始值附近的雅可比矩阵。

误差函数可以进一步写成

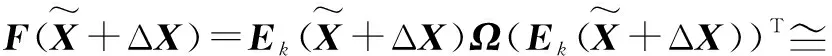
(14)

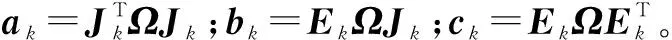
式(14)简化成

∑ΔXTakΔX=c+2bΔX+ΔXTaΔX

(15)

式中：a=∑ak；b=∑bk；c=∑ck。

对式(15)进行求导，并令其等于零，可得

aΔX=-b

(16)

状态最优结果可以简化求解式(16)，为了获得更加鲁棒的解，通常引入参数λ进行求解，即

(a+λI)ΔX=-b

(17)

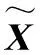
(18)

在设定的循环次数范围内通过不断地循环计算，获得最优的状态估计，基于图优化的深组合导航系统最优状态估计结构如图3所示，其中，Φk-1,k表示状态转移矩阵。

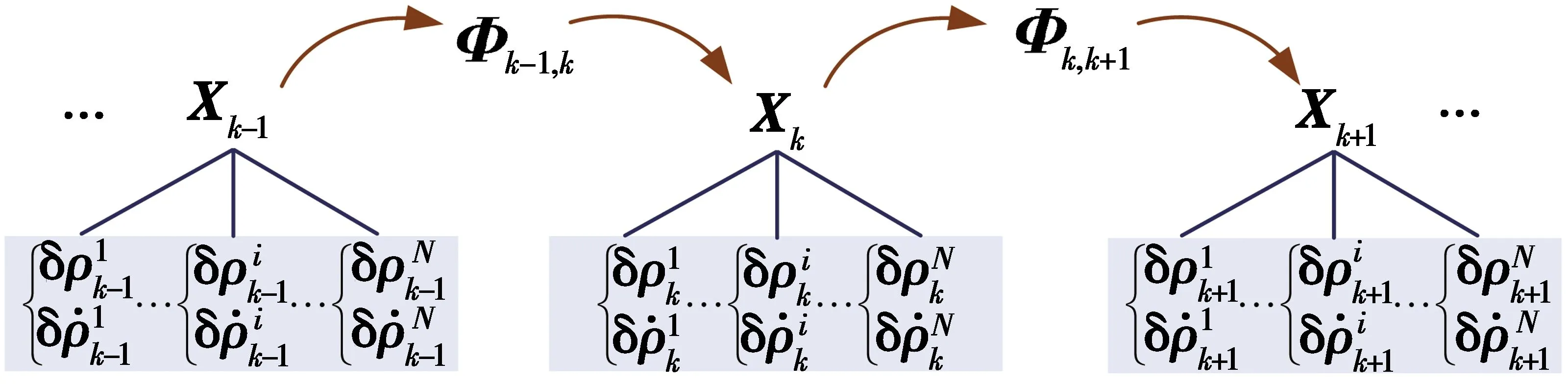
图3 基于图优化的深组合导航系统最优状态估计结构图Fig.3 Structure diagram of optimal state estimation of deep integrated navigation system based on graph optimization

3 仿真实验和分析

为了验证本文设计方法的有效性，利用仿真实验对算法性能进行分析和评估。首先通过轨迹发生器产生轨迹信息，然后导入卫星导航模拟器产生GPS卫星导航信号，通过中频信号采集器采集卫星导航系统模拟器产生的信号。采集的中频数据中频值为4.02 MHz，采样率为10 MHz。在Matlab环境下，基于GPS软件接收机搭建了深组合仿真系统，GPS软件接收机处理中频数据并与仿真的惯性导航数据进行深组合融合。惯性导航数据采样率为1000 Hz，与GPS卫星导航软件接收机更新频率保持一致，软件接收机基带信号处理更新时间为1 ms。惯性测量单元仿真参数如表1所示。

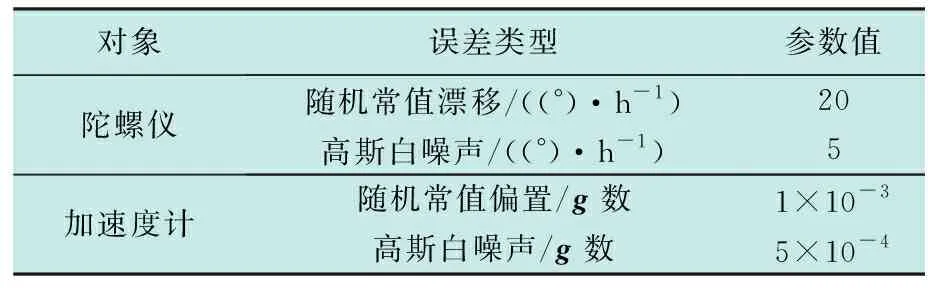
表1 惯性测量单元仿真参数Table 1 Simulation parameters of inertial measurement unit

仿真结果如图4、图5所示，数据分析结果如表2、表3所示。图4为本文研究的基于图优化的深组合导航方法三维位置误差曲线，以及传统卡尔曼滤波方法三维位置误差曲线。

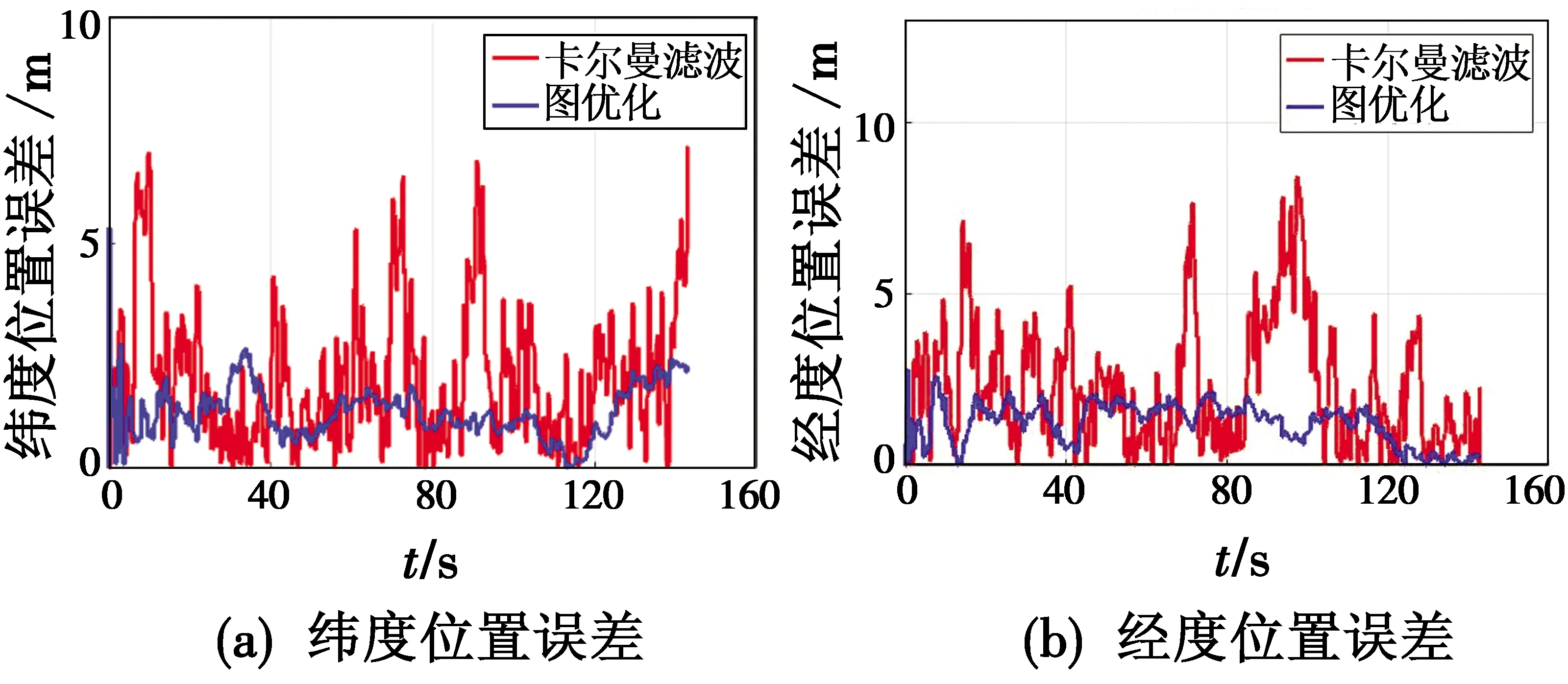
图4 三维位置误差曲线Fig.4 Three dimensional position error curves

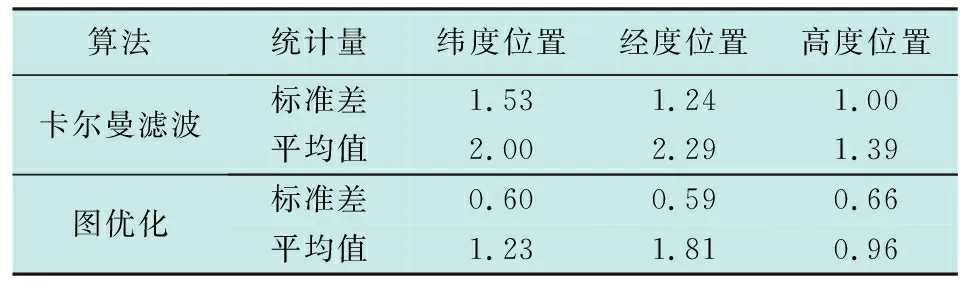
表2 三维位置误差Table 2 Three dimensional position error m

由图4可看出，相比于卡尔曼滤波方法，图优化算法在纬度、经度、高度方向的位置误差均有明显减小。表2给出了两种方法在三维方向误差的标准差和平均值，可以看出，与卡尔曼滤波方法相比，本文研究的图优化算法三维各向位置误差的标准差分别减少了60.8%，46.6%和31.3%，三维各向位置误差的平均值分别降低了38.5%，21.0%和30.9%，仿真曲线和数据分析结果表明，本文研究的算法能有效减小三维位置的定位误差。

图5所示为基于图优化的深组合导航算法以及传统卡尔曼滤波方法分别在东向、北向、天向的速度误差曲线。表3为两种方法在三维方向速度误差的标准差和平均值。

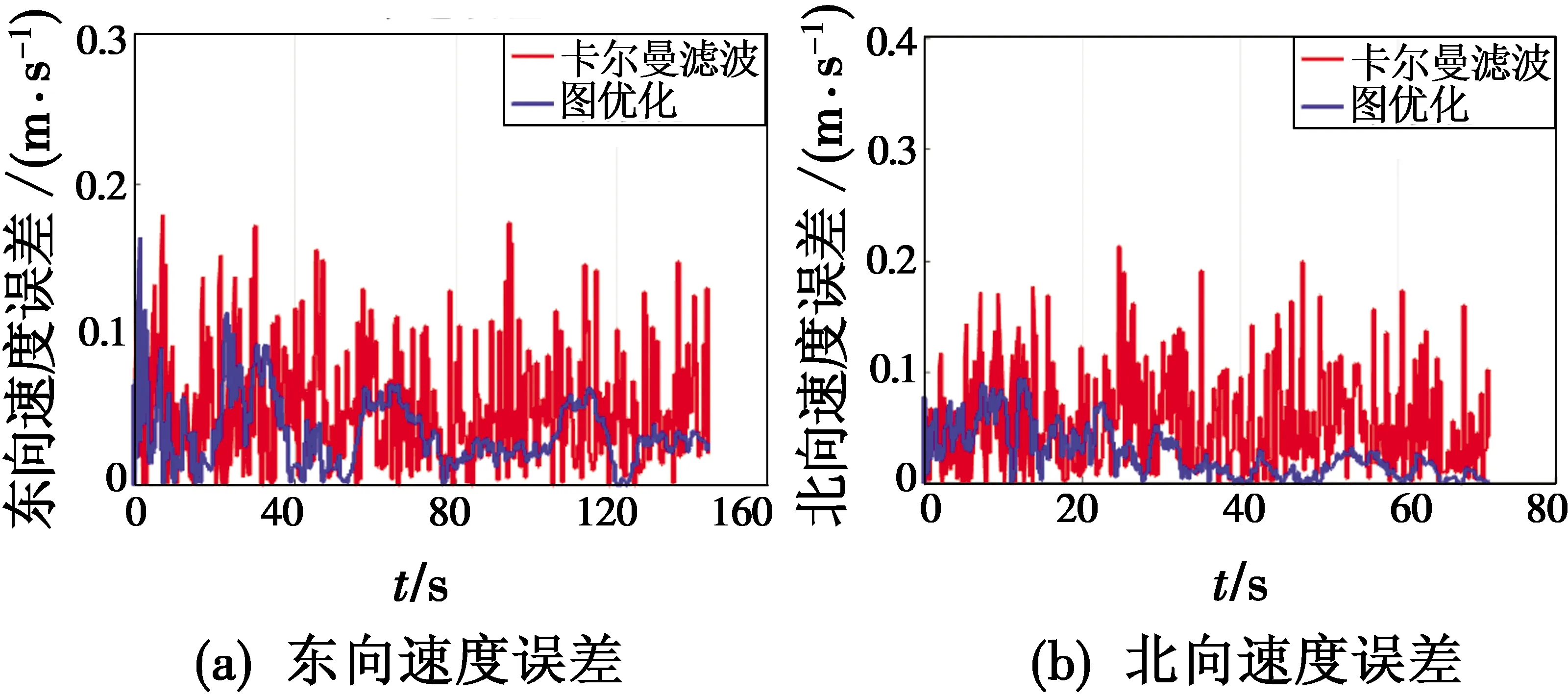
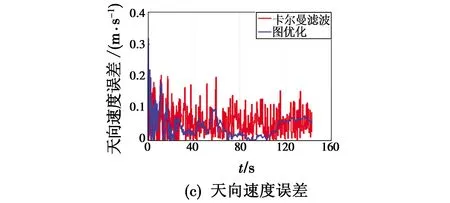
图5 三维速度误差曲线Fig.5 Three dimensional velocity error curves

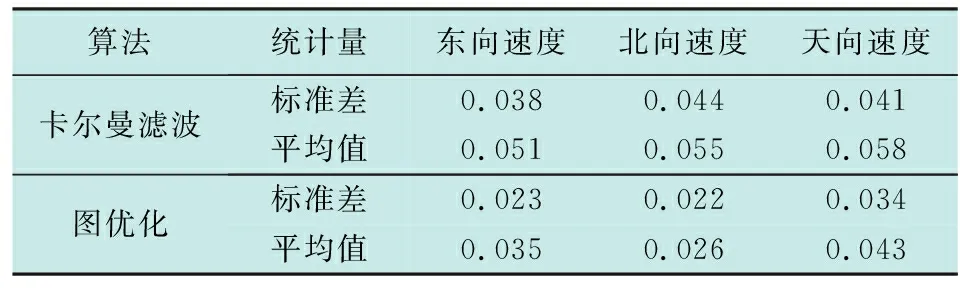
表3 三维速度误差Table 3 Three dimensional velocity error (m·s-1)

对图5和表3进行分析可以看出，与卡尔曼滤波方法相比，图优化算法在东向、北向、天向的速度误差均有明显减小，其中，图5(a)所示的东向速度误差的平均值和标准差分别减少了31.4%,39.5%，图5(b)所示的北向速度误差的平均值和标准差分别减少了52.8%,50.0%，图5(c)所示的天向速度误差的平均值和标准差分别减少了57.3%,17.1%。

由此可见，本文研究的基于图优化的深组合导航方法能有效减小东向、北向、天向的速度误差，这主要是因为图优化算法将更多的历史信息与当前信息同时用于优化求解，充分利用了状态之间的联系，有效减少了前一时刻误差对当前时刻估计的影响；同时，图优化算法在求解最优估计时采用了多次迭代，有效避免了模型的非线性对估计结果的影响。

4 结束语

针对将传统卡尔曼滤波方法用于INS/GNSS深组合导航系统定位时忽略历史信息的问题，本文研究了一种基于图优化的深组合导航滤波数据融合算法，通过将误差状态转移和量测信息作为约束条件构建优化的代价函数，并通过列文伯格-马夸尔特法求取状态的最优估计，充分考虑了历史信息对当前定位精度的影响。通过仿真实验对本文提出的算法进行了验证和评估，结果表明，图优化算法能有效提高INS/GNSS深组合导航系统的定位精度。