基于改进协同量子粒子群的小波去噪分析研究

周建新， 周凤祺,b

(华北理工大学，a.研究生学院; b.电气工程学院，河北 唐山 063000)

0 引言

信号消噪过程中，由于小波技术可以把信号的非平稳特性清晰地表现出来，所以小波变换的应用十分广泛。

小波去噪的重点包括阈值的估计值和阈值函数处理小波系数。小波阈值降噪中，阈值函数的选择至关重要。然而，传统的软硬阈值函数存在缺陷，无法完美还原信号，因此很多方法对阈值函数进行了改进。

为了求取阈值，袁开明等[1]将模拟退火算法引入阈值选取，并用一种新型的带参数阈值函数求解阈值，获得了极好的效果;唐鹏等[2]为了降低有用信号的畸变失真，提出一种新型的阈值函数，并将贝叶斯阈值引入小波变换;卢广森等[3]提出了一种新算法来确定分解层数和小波基函数，同时引入粒子群优化算法进行参数优化;对于受到污染的高频信号，吴雅静等[4]提出了将小波变换和粒子群互相结合的方法;相荣荣[5]对协同量子粒子群算法进行优化改进，并将其成功应用于医学图像分割方面。

本文提出一种基于改进的协同量子粒子群优化(CQPSO)小波阈值算法。为了避免粒子陷入局部最优，提高全局寻优能力，改进自适应收缩扩张因子。用改进的协同量子粒子群算法优化小波阈值函数中的调节因子和阈值，使它们的数值取值最优，通过数据结果与仿真图像表明，该算法能较大限度地使阈值函数参数取值最优，去噪效果佳，较好地还原信号。

1 新型协同量子粒子群算法

1.1 协同量子粒子群算法的改进

大部分的随机搜索算法都存在维数灾难问题，即随着维数的增多，搜索算法的性能会随之降低，同时，种群的多样性也会减少。种群中粒子的每一维决定相对应的适应度值。尽管部分粒子某一维的数值已经达到全局最优，但因为维数的问题，最终粒子被舍弃，即最优粒子不能被完美利用。为了避免这种情况，本文参考文献[5]的改进型协同量子粒子群算法，即考虑到粒子之间的协同作用。利用蒙特卡罗多次测量产生多个个体，再通过协同算法计算出新的个体，即经过多次测量后，选出数值最优的5个个体，再根据适应度值的大小挑选出最优的一个，设为Xl 0(x00,x10,…,xl 0)，同时将其设为背景变量，即Xc=Xl 0，令Xi=Xl 0(Xi为粒子的当前位置)，再用Xl 1(x01,x11,…,xl1),Xl 2(x02,x12,…,xl 2),Xl 3(x03,x13,…,xl 3),Xl 4(x04,x14,…,xl 4)每一维分量的数据来替代背景变量Xc中相应维度变量的数据，将其设为新的背景变量X′c，再计算X′c的适应度值，若优于Xc的适应度值，则表明该维分量的数据是更优的，那么就用这个数据替代Xi中的原数据，得到最终的Xi[6]。

由于收缩扩张因子取值过大会导致算法搜索精度低，取值过小则不能跳出局部最优解[7]，因此在文献[8]的基础上，对自适应收缩扩张因子进行改进。

定义进化速度因子f(t)为

(1)

式中,F(gbest(t+1))和F(gbest(t))分别为粒子在第t+1次和粒子在第t次全局最优位置的适应度值，gbest(t)为粒子的个体最优值。本文选取信号间的均方差评估去噪效果。

文献[8]的自适应收缩扩张因子为

α=α1-f(1)×α0

(2)

式中:α0为α初值，一般取值为1；α1为速度因子权重，一般取值为0.5。该收缩扩张因子在取值方面获得了进一步的优化，但因为收缩扩张因子需要根据f(t)的不同而取不同的值，因此，本文提出如下自适应收缩扩张因子

βt=βt-2-(f(t-2)-1)×βt-1t>3

(3)

式中：若t=3时，β3=β2-f(1)×β1，β2为初值，通常取值1，β1为速度因子权重，通常取值0.5，βt∈[0.51]，βt若大于1取1，小于0.5取0.5。

当f(t)值较小，粒子距最优位置远，全局最优适应度值变化较大，收缩扩张因子增大以便快速寻优;当f(t)值较大，粒子距最优位置近，全局最优适应度值变化小，收缩扩张因子减小以精确寻优;当f(t)值为1时，进化停止。

协同量子粒子群算法位置更新算式为

(4)

式中：βt为自适应收缩扩张因子；Xi d(t+1)为第t+1次、第i个、第d维新个体的粒子位置；pi d(t+1)为第t+1次、第i个、第d维mbest(t)和gbest(t)之间的随机位置；mbest(t)为第t次的平均最佳位置，算式为

(5)

pi d(t+1)=μ1×pbest(t)+μ2×gbest(t)

(6)

式中：M为粒子数量；pbest，i d(t)为第t次、第d维、第i个粒子的局部最优值；μ1,μ2∈rand(0,1),当适应度值取最优，Xi d(t+1)所在的粒子位置即是gbest(t+1)。

1.2 基于改进协同量子粒子群的小波变换

阈值函数在小波阈值降噪过程中十分重要。虽然软硬阈值函数有许多优点，但在实际应用中仍有很大的改进空间。因此，很多文献提出带参数的阈值函数，但鉴于阈值函数中参数无法取得最优值，去噪效果不尽如人意。

本文提出一种基于改进协同量子粒子群优化小波阈值函数的算法用于去噪领域，即用改进协同量子粒子群算法优化小波阈值函数中的调节因子和阈值，使它们取值最优，从而达到更好的优化效果。

本文采用的阈值函数为文献[9]所采用的阈值函数，即

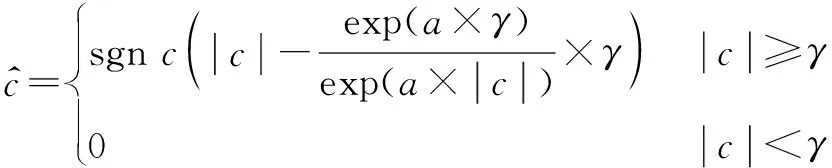
(7)

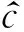
适应度值的选取。在本文中，选取信号之间的均方差作为算法的适应度函数[9]，即

(8)

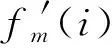
1.3 基于协同量子粒子群的小波变换去噪步骤

1) 对协同量子粒子群中的参数初始化。将所有粒子位置设为Xi(0)，个体最优值为pbest,i(t)=Xi(0)。本文设置个体维数为2。

2) 计算所有粒子的适应度值，并计算群体的pbest(t)和mbest(t)。

3) 对于每个个体最优，通过蒙特卡罗多次观测得到5个个体。根据协同量子粒子群算法的更新式[11]得到第1维数据，然后再根据协同量子粒子群的更新式得到第2维数据，若比第1维数据更优(即均方误差更小)，则将此数据作为第2维，否则，将第1维数据减0.5得到第2维数据[11]，以此类推得到每一维数据。

4) 对适应度值进行选择比较。根据适应度值越小，适配值越好的原则，选出最优个体,设为X(t+1)，并将其设为背景变量L(t+1)，同时将它与其他4个个体的每一维交换，得到X′(t+1)，评价X′(t+1)，若比X(t+1)好，则替代X(t+1)，即该维中包含的数据替换原始维数的数据，否则不变[12]。当适应度值取最优，Xi d(t+1)所在的粒子位置即是gbest(t+1)。最终得到gbest(t+1)和pbest(t+1)。

5) 判断是否到达停止条件，然后计算得到最终的gbest。否则，返回3)，并继续计算。将两次gbest第2维的数值分别作为γ与a，最终得到优化后的小波阈值函数。本文中设定的最高迭代次数为300。

6) 用式(7)对小波系数进行阈值化处理，利用阈值化后的小波系数重构得到最终结果。

2 仿真结果研究

信噪比(SNR)和均方根误差(RMSE)是评价去噪效果的标准。RMSE小，去噪效果好[13]，即

(9)

SNR数值越大，去噪效果越好[14],即

(10)

式中:f(m)为含噪信号;r(m)为去噪后的信号[15]。

本文做出以下假设，将一般的粒子群算法优化小波阈值函数中参数的算法设为算法A，量子粒子群优化小波阈值函数中参数的算法设为算法B，协同量子粒子群优化小波阈值函数中参数的算法设为算法C，将本文提出的算法设为算法D。表1为各类算法去噪效果数值的比较。

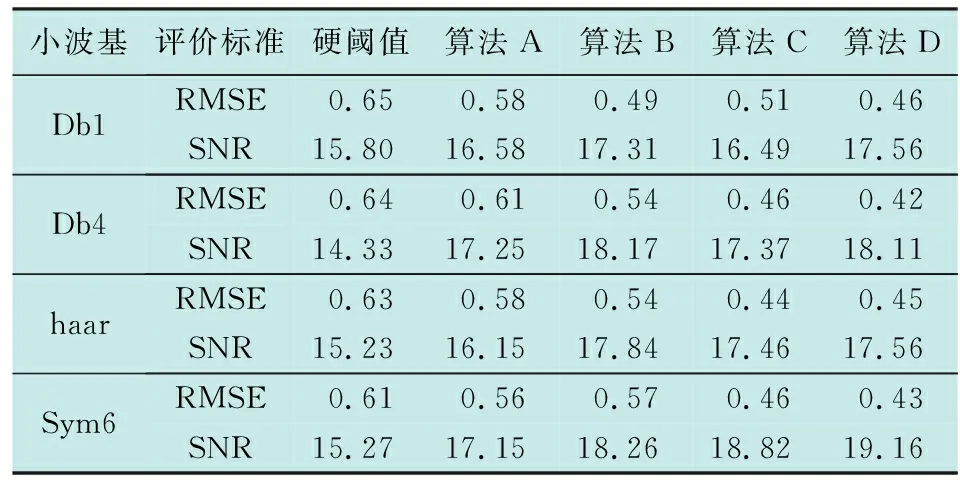
表1 不同小波基下各类算法的去噪效果数值比较Table 1 Threshold denoising effect of different algorithms under different wavelet bases

由表1可知，算法D的数值优于其他算法。表2为算法D在不同评价标准下相比其他算法的提升率，其中，负数值表示算法D相比其他算法性能有所下降。

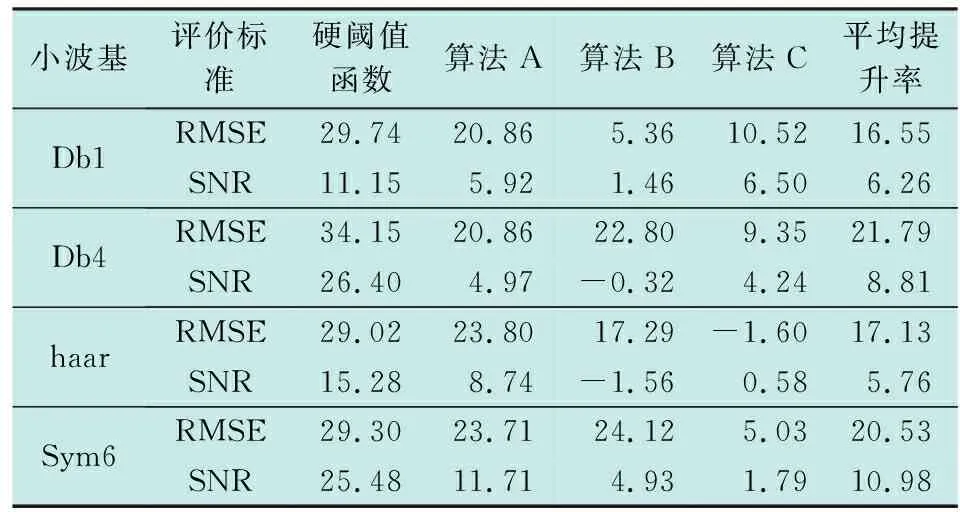
表2 不同小波基下算法D相比其他算法的去噪效果数值提升率Table 2 Numerical improvement rate of denoising effect of D Algorithm under different wavelet bases %

从表2可以看出，在协同量子粒子群中引入自适应收缩扩张因子是合理的。在SNR的评价标准下，算法D相比于其他算法的平均提升率约5%～10%。在RMSE的评价标准下，算法D相比其他算法的平均提升率约16%～20%。以上数据表明，本文算法即算法D的去噪能力略好于其他各类算法。图1所示为原信号、含噪信号及各算法的去噪图像。

由图1可知，算法A去噪效果并不理想，图像曲折不平，且凹凸处较明显。因为阈值函数中的参数并非最优，粒子群算法的粒子难以跳出局部最优。引入量子粒子群和协同量子粒子群算法后，算法B和算法C在去噪效果上都有一定增强，曲线更为平滑，而算法D虽然在波谷有些许误差，但在信号去噪效果上优于算法B和算法C。

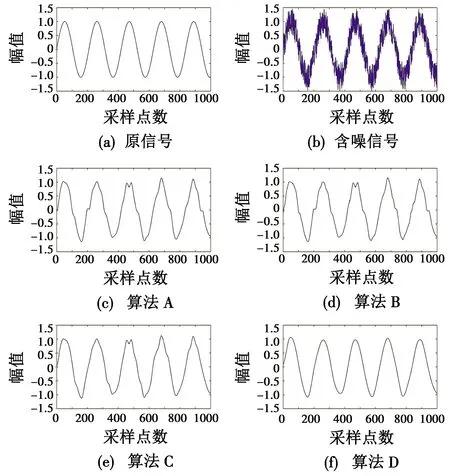
图1 原信号、含噪信号及不同算法的去噪图像Fig.1 The original, noised,and denoised images of different algorithms

3 结论

本文将自适应收缩扩张因子引入到协同量子粒子群算法，利用改进协同量子粒子群算法对小波阈值函数中的调节因子和阈值进行优化，再利用阈值函数对含噪信号进行阈值处理，重构后即可得到最优的去噪信号图。通过对比仿真实验的数据可知，本文算法在SNR的评价标准下，相比于其他算法提升5%～10%;在RMSE的评价标准下，相比其他算法提升16%～20%。通过对比其他算法可得，本文算法的去噪图像更为平滑，能更好地反映原信号的特征。因此,本文算法在去噪方面有一定优越性，各项指标及去噪效果略优于硬阈值函数、粒子群优化阈值函数和量子粒子群优化阈值函数等算法，能较好地保留原信号特征。