高阶非线性未知系统的ACPI控制方法
2022-01-22许惠清曾喆昭陈泽宇
许惠清, 曾喆昭, 陈泽宇
(长沙理工大学电气与信息工程学院,长沙 410000)
0 引言
非线性未知系统的控制问题一直是控制理论与控制工程领域的研究热点问题之一。目前,针对非线性未知系统的主要研究方法有PID控制[1]、滑模控制(SMC)[2-5]、自适应神经网络控制[6]、自适应模糊控制[7]及其各方法之间的复合控制[8-9]等。当系统内外扰动满足匹配条件时,上述方法能够较好地跟踪控制,然而,其控制器结构复杂,计算量较大,且当干扰不再满足匹配条件时,难以直接应用。针对一类含有非匹配干扰的非线性未知系统控制问题已有很多研究方果。文献[10-11]将干扰观测器与滑模控制相结合,对干扰进行估计和补偿,提高系统的跟踪控制效果。文献[12]将有限时间干扰观测器与多幂次积分型滑模控制策略相结合,并用于永磁同步电机的控制,通过积分型滑模面有效消除传统滑模控制中的“抖振”现象,实现估计误差在有限时间内收敛到零,然而控制器参数较多,计算量大。文献[13-20]将反步控制与滑模控制相结合,有效解决了高阶非匹配非线性系统控制问题。其中,文献[13]通过引入低通滤波器避免传统反步控制中存在的“微分爆炸”现象,并使用了一种积分终端滑模控制削弱控制器抖振;文献[14-17]将反演控制与滑模控制相结合,并通过干扰观测器消除非匹配干扰的影响,提高系统的收敛速度,然而,文献[14]并不能很好地解决反步控制中的“微分爆炸”问题,文献[16]需要依赖扰动观测器的高增益参数;文献[18-20]在控制的前n-1步通过反步法抑制非匹配项对系统的影响,最后一步设计滑模控制器,使系统达到快速收敛的目的。尽管这些方法针对具有非匹配干扰的非线性系统控制问题取得了一定的效果,但其控制器结构复杂,参数较多、计算量大。
为了有效解决现有控制方法存在的局限性,并进一步提高控制系统的动态品质与稳态性能,本文针对含有非匹配干扰的高阶非线性未知系统,基于自耦比例-积分(Auto-Coupling Proportional-Integral,ACPI)控制理论[21],提出一种基于虚拟递推控制的ACPI控制方法,将各虚拟指令的微分定义为未知有界扰动,从而避免了反步控制中存在“微分爆炸”的问题,并使用一种与被控对象模型无关的自适应速度因子模型。由于该方法只涉及一个速度因子需要镇定,而且该控制系统具有良好的抗扰动鲁棒性和大范围鲁棒稳定性,因而是一类控制器结构简单、便于实际应用的傻瓜型控制方法。
1 系统描述
考虑如下含有建模误差和未知扰动的n阶非匹配非线性系统
(1)
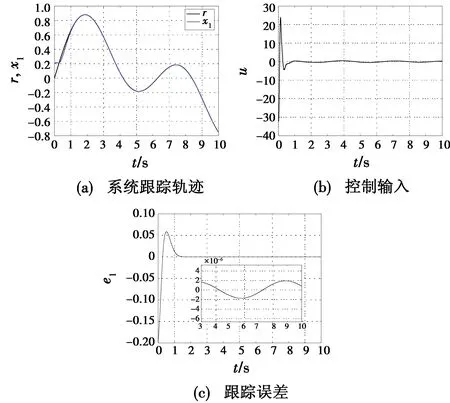
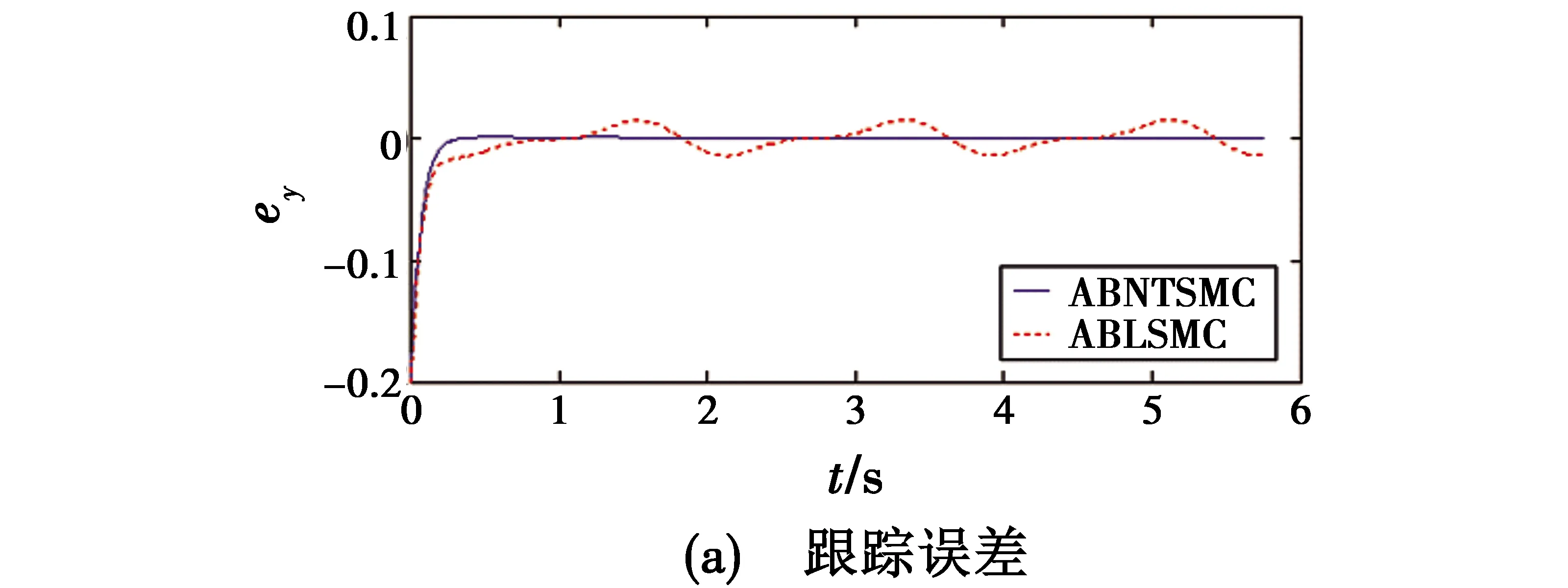
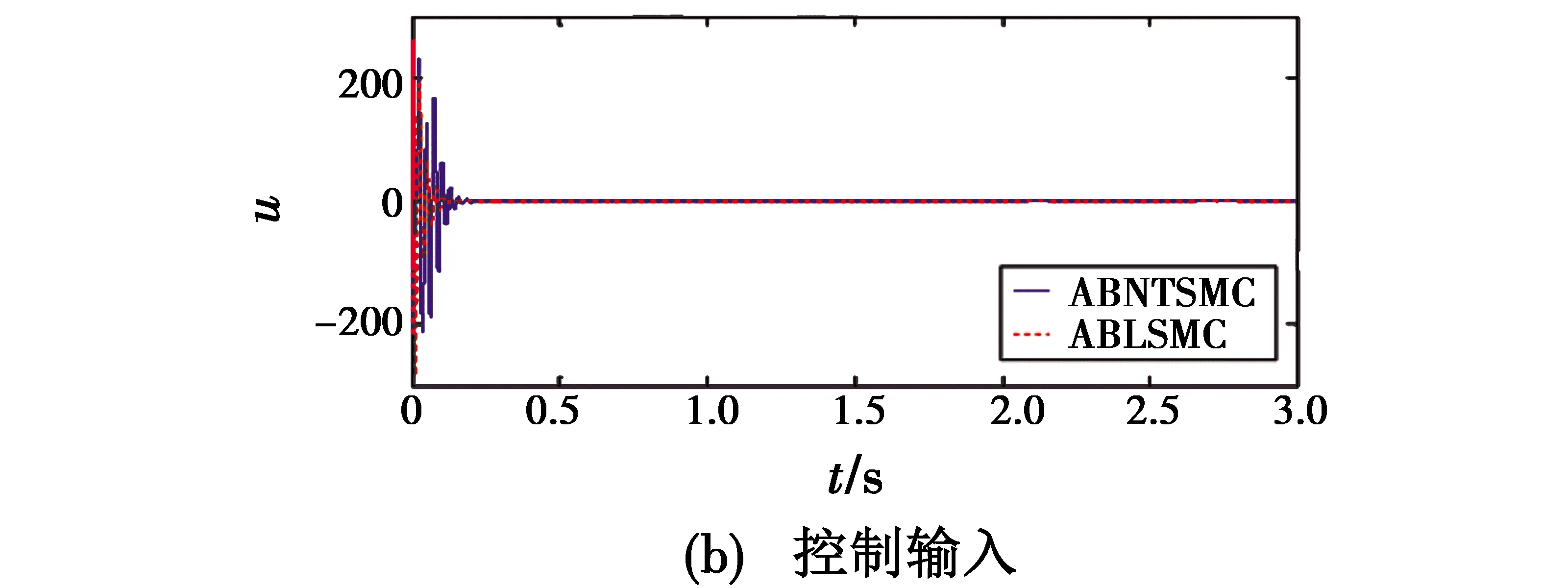
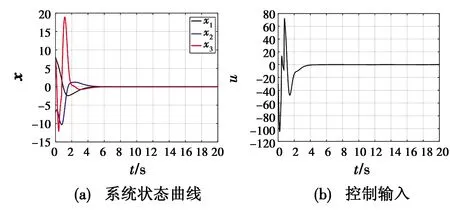
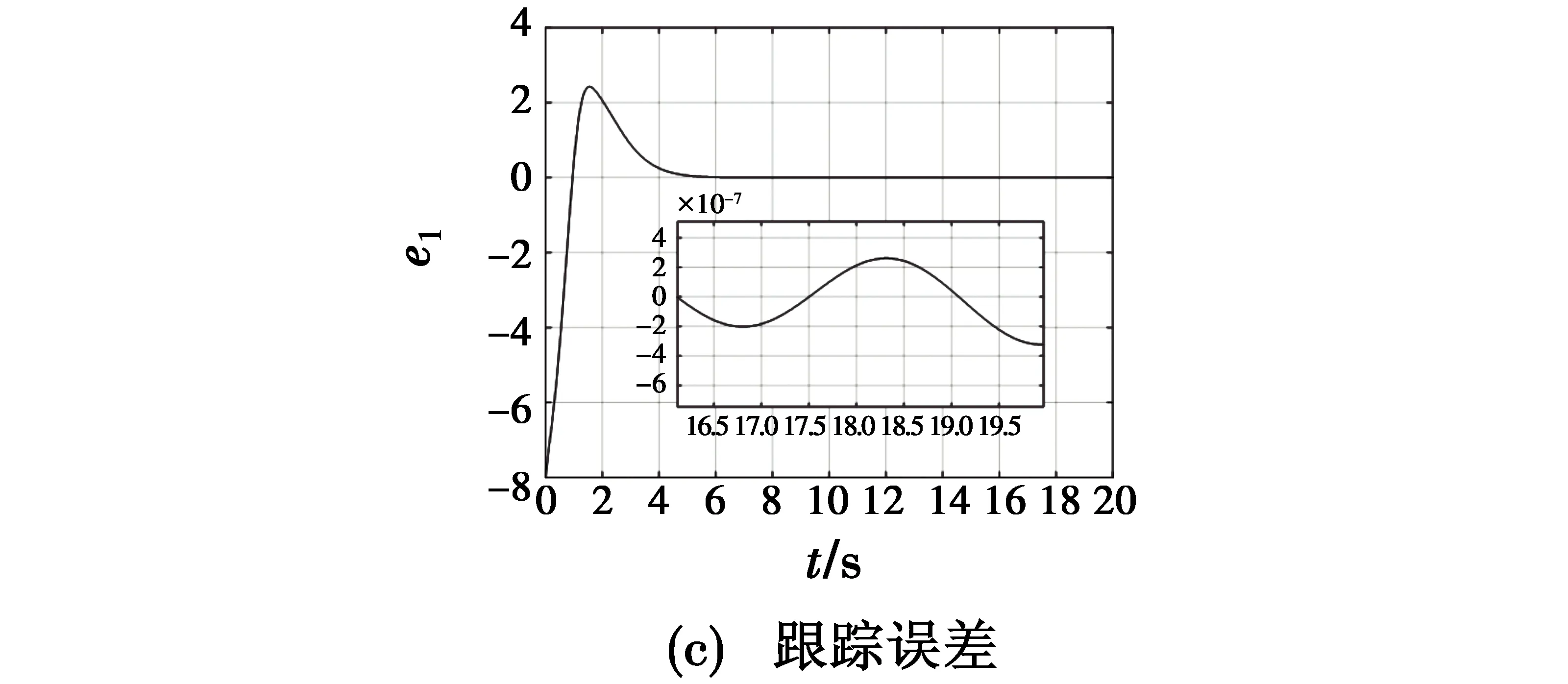
式中:x=[x1x2…xn]T∈R,为可测系统状态向量;f(x)为关于状态向量x的未知非线性函数;0 则系统式(1)可以映射为 (2) 因系统式(2)是系统式(1)的等价映射,因而由系统式(2)设计的控制器u可以实现对系统式(1)的有效控制。 (3) (4) 式中:zc1>0,为速度因子;|u1i|≤0.5y2dm;|y2d|≤y2dm。 (5) (6) 式中:zc2>0,为速度因子;|u2i|≤0.5y3dm;|y3d|≤y3dm。 (7) j=1,2,…,n 式中:zc(j-1)>0(j=1,2,…,n),为速度因子;|u(j-1)i|≤0.5yj dm;|yj d|≤yj dm。 当j=n时,由式(7)得虚拟指令为 (8) (9) (10) 式中,zc n>0,为控制器的速度因子。 设计基于虚拟递推控制器的闭环控制系统,能够有效实现系统各个状态的递推跟踪控制,即y=y1→r,y2→y2d,…,yj→yj d。 由定理1可知,当zc j>0(j=1,2,…,n)时,基于虚拟递推控制的ACPI闭环控制系统是大范围鲁棒稳定的,表明速度因子在zc j>0的范围内具有很大的镇定裕度。然而,速度因子较小会使ACPI控制力过小,降低闭环控制系统的响应速度与抗扰动能力;速度因子过大,又会因积分控制力过大而引起超调与振荡现象。因此,在满足定理1的稳定性条件下,本文使用一种自适应速度因子模型为 zc j=zcm(1-0.9e-t)j=1,2,…,n (11) 式中,0 由于0 实验1。考虑如下含有建模误差的三阶非匹配非线性系统[14,18] (12) 式中:d1=0.5sin 2t+sint;d2=te-0.5t;d3=0.8sint;建模误差F=0.01x2e-0.5x1。 设初始状态x0=[0.2,0.5,0.5]T,跟踪指令信号为xd=0.5(sint+sin 0.5t),采样步长h=0.001 s,b0=5,3个速度因子分别取值为zc1=13(1-0.9e-t),zc2=60(1-0.9e-t),zc3=200(1-0.9e-t),虚拟指令与控制器u的幅值限定分别取|y2d|≤10,|y3d|≤50,|u|≤100,仿真结果见图1,文献[14,18]控制方法的仿真结果见图2。 图1 本文控制方法仿真结果(实验1)Fig.1 Simulation results of the proposed control method(Experiment 1) 由图1可知,本文控制方法可以在1.5 s内实现对参考指令的稳定跟踪控制,控制输入光滑、无抖振,跟踪精度较高(稳态绝对误差小于2×10-6);而文献[14]采用的自适应反步线性滑模控制(ABLSMC)输出稳态误差变化量小于2.1×10-2,文献[18]采用的自适应反步非奇异终端滑模控制(ABNTSMC)稳态误差变化量小于1.6×10-2。图2(b)为文献[14,18]的控制输入,两种方法的动态响应初期控制输入幅值都比较大,容易损坏执行机构,且控制器参数较多,参数调节困难,计算量大。 由图1与图2的对比可知,本文控制方法的稳态跟踪精度更高,动态响应初期的控制输入为文献[14,18]的1/10左右,且本文控制方法只有一个与被控对象无关的速度因子需要镇定,控制方法简单,便于实际操作。 图2 文献[14,18]控制方法仿真结果Fig.2 Simulation results of Reference[14,18] 实验2。为进一步验证本文控制方法的有效性,以文献[11]给出的磁悬浮系统为例进行仿真实验,即 (13) 式中:d1=0.04sint;d2=0.03cos 2t+0.01;d3=0.02sin 2t-0.01cost。 设初始状态为x0=[8-77]T,跟踪指令信号为xd=0,采样步长h=0.001 s,b0=1,3个速度因子分别取值为zc1=2(1-0.9e-t),zc2=8(1-0.9e-t),zc3=80(1-0.9e-t),虚拟指令与控制器u的幅值限定分别取|y2d|≤10,|y3d|≤30,|u|≤120,仿真结果见图3。 图3 本文控制方法仿真结果(实验2)Fig.3 Simulation results of the proposed control method(Experiment 2) 由图3(c)可知,本文控制方法能够在6 s内获得有效控制,稳态绝对误差小于4×10-7。图4所示为文献[11]控制方法的仿真结果,可知文献[11]需要10 s左右才能实现有效控制,且控制器参数多达12个。 图4 文献[11]控制方法仿真结果Fig.4 Simulation results of Reference[11] 比较图3、图4可知,本文控制方法中不仅控制器结构简单、便于实际应用,而且系统的响应速度更快、稳态精度更高。 针对高阶非匹配非线性未知系统的控制问题,本文使用一种基于ACPI控制理论的虚拟递推控制方法,将各虚拟指令的微分定义为未知有界扰动,从而有效避免了“微分爆炸”的问题。该方法借鉴文献[21]的ACPI控制理论思想,提出基于虚拟递推控制的ACPI控制器,并使用一种自适应速度因子模型,理论分析了闭环控制系统的全局鲁棒稳定性以及抗总和扰动鲁棒性。仿真结果表明本文控制方法具有良好的动态品质与稳态性能。与文献[11,14,18]相比,本文控制方法的控制器结构简单、稳态精度高、计算量小、便于实际应用,在含有非匹配干扰的高阶复杂非线性未知系统控制领域具有重要的参考价值。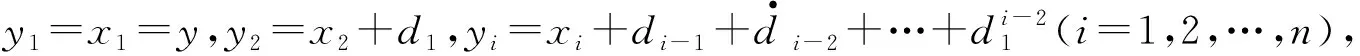
2 虚拟递推控制器设计
2.1 基于ACPI镇定规则的虚拟递推控制器
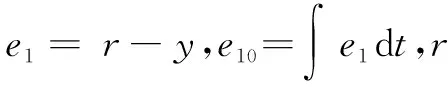

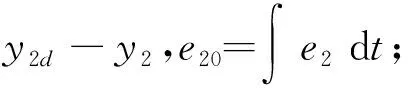
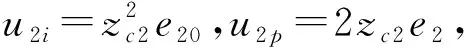
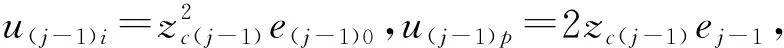
2.2 控制系统稳定性分析
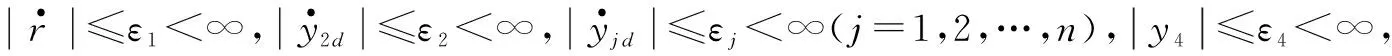
2.3 速度因子镇定方法
3 仿真分析

4 结论
