多热源冷板主散热通道的布局优化

王飞朝

（西安电子工程研究所，西安 710100）

0 引言

作为一种散热结构，冷板在电子设备结构设计中大量采用[1-6]。由于安装在冷板上的电子元器件较多，部分器件热耗较大，所以在冷板上有很多温度极大值点，而为了降低冷板上的最高温度，提高冷板的均温性，往往需要对组成冷板的金属板局部进行强化散热，例如采用有散热齿的风冷冷板、液冷冷板、预埋热管的冷板等。这些方法可以统一理解为在金属板上布置了一条或多条散热能力远远大于一般金属板的散热通道，可称之为主散热通道。对主散热通道进行合理的布局，可有效提高冷板的均温性，降低冷板。本文从工程实际出发，对于冷板主散热通道的布局优化提出了一种简单的解决办法，该方法特别适合于产品方案设计阶段。

1 分析模型

由于冷板的长度及宽度尺寸往往远远大于厚度尺寸，所以可以将冷板的导热简化为二维导热问题，不管主散热通道采用何种冷却方式，都可以理解为对金属板局部热阻的减少。例如图1为埋有热管的冷板，热管1和热管2处为低热阻，其余部分则为高热阻；图2的液冷冷板，包括液冷管路处的低热阻及普通金属板处的高热组；图3的风冷冷板，包括散热齿处的低热阻及普通金属板处的高热组。整个冷板的控制方程为二阶偏微分方程，一般很难得到其解析解[7-8]。本文采用二维耦合热阻网络建立冷板的分析模型。

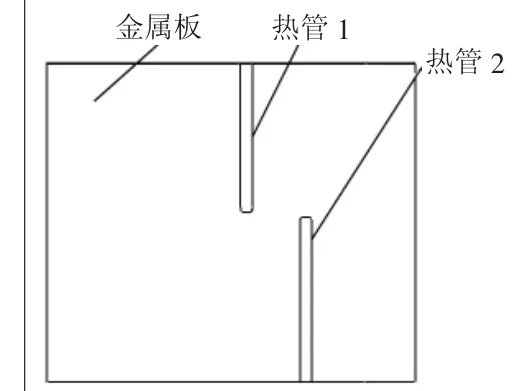
图1 埋有热管的冷板

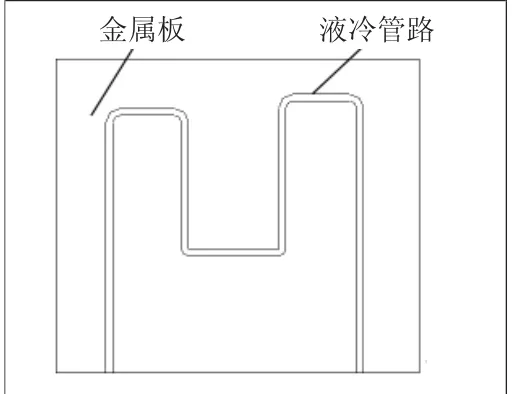
图2 液冷冷板

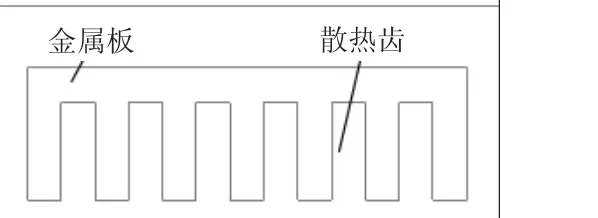
图3 风冷冷板

1.1 热源及主散热通道

为了便于分析问题，需要对冷板上的热源及主散热通道进行简化。对于热源而言,冷板上的功耗通过与冷板的接触面（一般为方形）传导到冷板上,功耗在该接触面上如何分布与热源的封装形式密切相关，考虑到热源与冷板的接触面相对于冷板的尺寸较小，温度在小平面上的变化不会太大，所以可以将热源等效为接触面上一些点热源的叠加，如何等效则取决于热源的封装形式、与冷板的接触面尺寸、热源的功率大小等,热源功率如下所示：

式中：P为热源的实际功率；Pj为等效的点热源的功率；n为点热源数。

实际等效时，应针对具体问题进行具体分析，例如可将热源等效为几何中心的点热源，或者等效为接触面4个角上的点热源等。

对于主散热通道而言，其在同一通道横截面上各处的温差很小，所以在布局优化时，可以将散热通道等效为多根相互垂直并首尾相连或不相连的直线段，这些线段的起点、终点及交点定义为特征点，显然由所有的特征点的坐标便可以确定主散热通道的布局，这也为后面的布局优化提供了一种简便的方法。

1.2 网格划分

在不刻意追求计算速度的情况下，为了编程的简便，可以以1 mm为步长，划分纵横网格线，形成多个节点。

也可采用不均匀划分的方法，将网格划分分为两步：1）通过所有的热源点用一系列与坐标轴平行的网格线划分成很多子区域，生成多个节点；2）接着对前述网格线进行不均匀划分，生成新的网格线。划分策略为：如果某一条网格线上的热源总热耗较大，则在其与前后或上下的网格线之间生成新的网格线以加密网格，如果某一条网格线上的热源总热耗较小，则无需在其周围加密网格。

1.3 建立模型

根据以上2个简化，就可以采用二维耦合热阻网络建立含有主散热通道的冷板模型。图4所示为一简单冷板，其外形尺寸为a×b，冷板内含有9个点热源，主散热通道由3条线段组成，将3个线段的4个端点可以定义为特征点，即由4个特征点就能描述3个线段上的所有点。显然图中的内部节点与周围4个节点发生关系，边界节点则与2个或3个节点发生关系。下面就可以建立通用的冷板二维热阻网络模型,建立的基础是傅里叶定律及能量守恒定律。

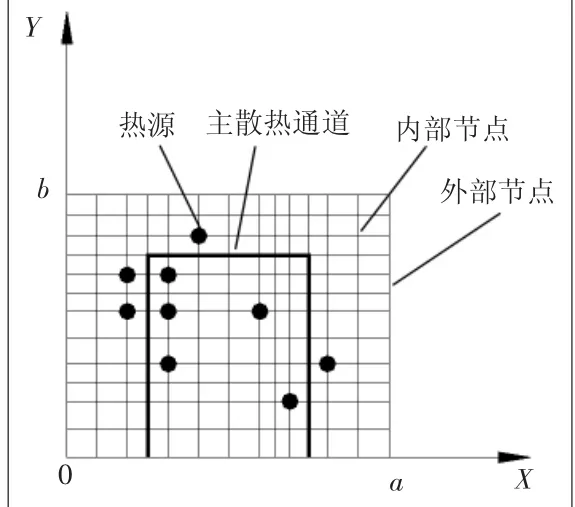
图4 冷板示意图

对于所有的内部节点Pi，j（其中1＜i＜n，且1＜j＜m）而言，如图5所示，存在方程：

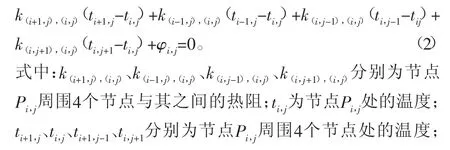
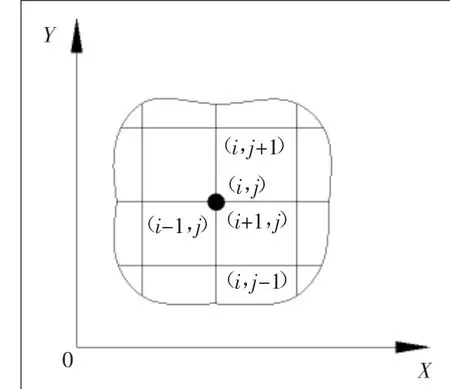
图5 内部节点示意图

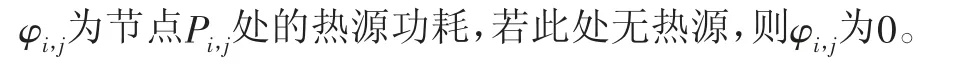
对于边界节点则可以写出8个方程, 分别针对4个角点，及冷板4个边上的节点（不包含4个角点）。

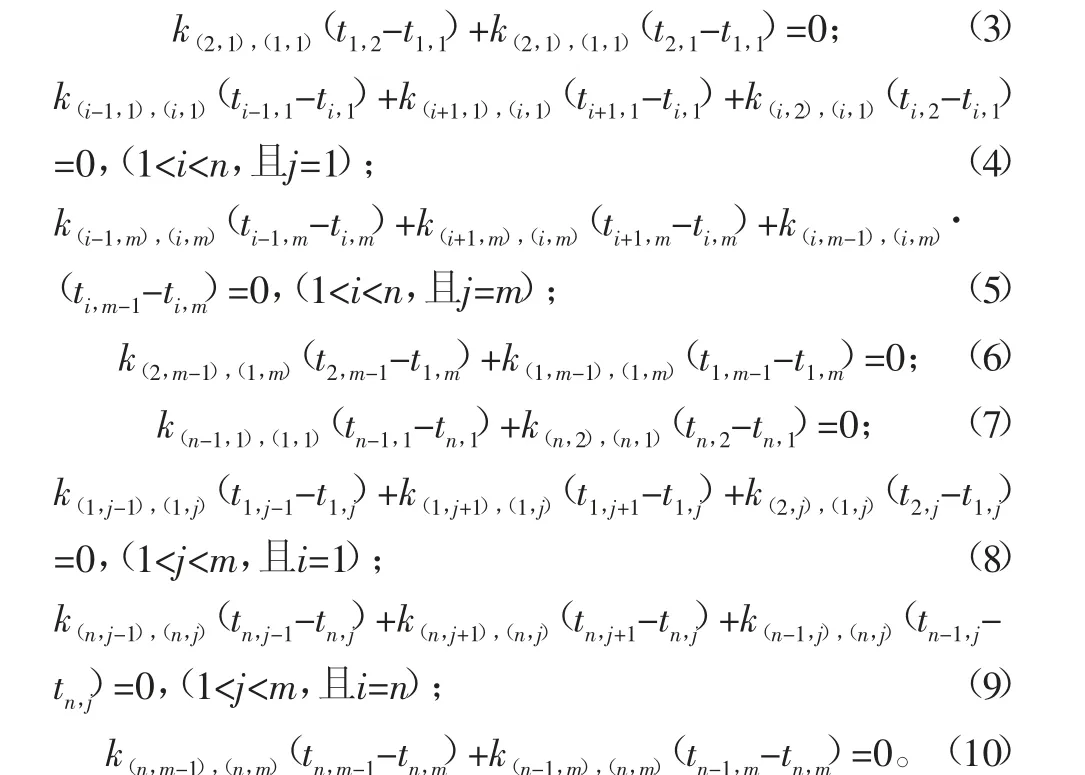
主散热通道上的节点之间的热阻值跟主散热通道的散热方式有关，当散热方式确定后，其值大小就可计算得出。本文给出一种简便的处理方法，即对于主散热通道上2个相邻点的热阻，可以认为是对应金属板热阻的a倍，a远远小于1，这样假设并不影响冷板局部温度极大值点的分布，对于各个节点具体温度值的计算，也有相当的精度。

对于非主散热通道上的节点，则可以求出，例如内部节点Pi，j的k（i+1，j），（i，j），其值为

式中：K为n×m行，n×m列；T、Φ为n×m列。

虽然有n×m个方程，但K主对角线上的所有元素均为同一行其余热阻值之和求负，所以热阻矩阵非满秩，独立的方程数为n×m-1个，而自变量数为n×m个，故只需知道某一个节点的温度，就可以求出其余所有节点的温度。

2 布局优化编程

2.1 优化模型及算法选择

在前面分析的基础上，可以建立该问题的优化模型：

优化目标为所有节点的最高温度值趋于最小，自变量则为主散热通路的特征点qxy，约束条件包括两种：1）满足线型方程组KT=-Φ，任何此类型的优化问题都必须满足该约束条件；2）约束条件是某一具体问题的已知量，例如式（13）中的主散热通道上的输入点及输出点温度已知，当然该种约束会因为不同的具体问题而会有不同的表达公式。

主散热通道的布局优化为一种组合优化问题。MATLAB软件带有遗传算法工具箱可供采用[10]，ga函数的格式如下：

2.2 编程方法

根据分析可知，采用MATLAB软件进行编程求解，流程如图6所示。由该流程可以看出，大量的计算是对由热阻矩阵组成的线性方程组的求解，同时多次调用GA函数。对于适应度函数,工具箱提供了适应度的尺度变换函数。选择操作函数包括随机均匀分布选择法、赌轮盘选择法、剩余选择法等。交叉函数包括高斯变异均匀变异等。停止条件定义了算法终止的条件，GAOT中设置的参数有最大代数、最大时间、适应度限、停滞代数等。

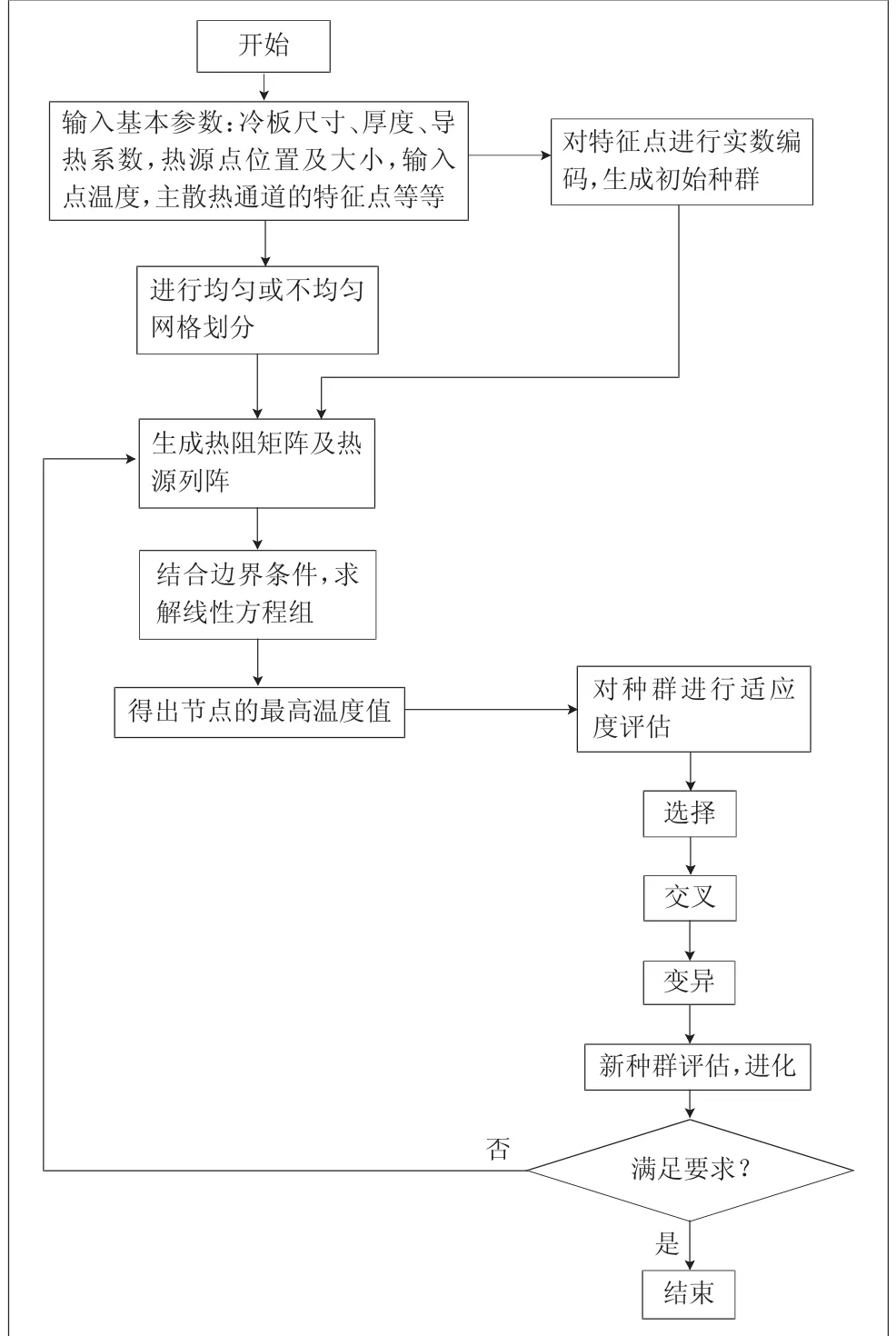
图6 求解流程

3 算例

某冷板规格为200 mm×160 mm,板厚为3 mm，其上有5个热源，其功率大小分别为20、10、5、15、8 W，采用液冷散热，液体输入温度为50 ℃，进口及出口均位于短边上，给出两种主通道的布局，主通道布局的特征点为4个，求其最优的热通道布局。

首先建立冷板的网格图，如图7所示。计算可得分别采用主散热通道1及主散热通道2时各热源点的温度值如表1所示。计算所有节点的温度网格图如图8～图9所示。

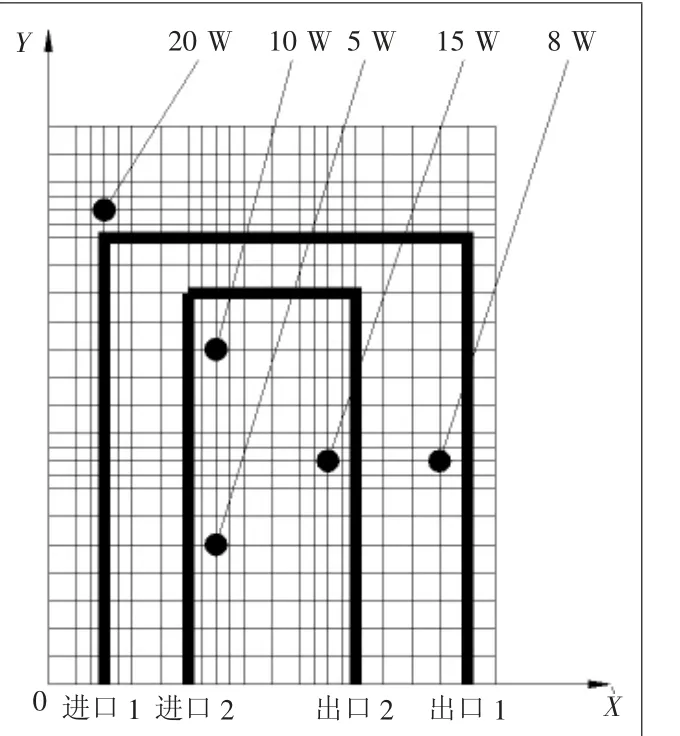
图7 冷板网格图

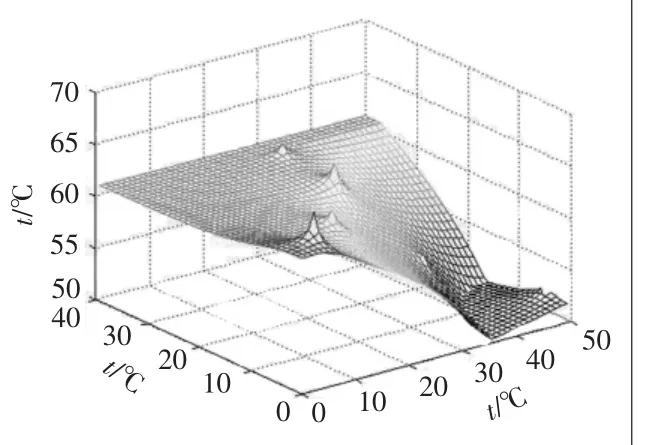
图8 通道1的冷板节点温度网格图

采用前述方法进行布局优化求解，可得优化后的冷板各节点温度网格图如图10所示。方案1、方案2及优化后的冷板各热源点的温度值如表1所示。

图10 优化冷板节点温度网格图

由表1 可以看出冷板2相对于冷板1散热效果好，最高温度低了2 ℃，而优化后，则最高温度仅有54 ℃，冷板的均温性明显提高。

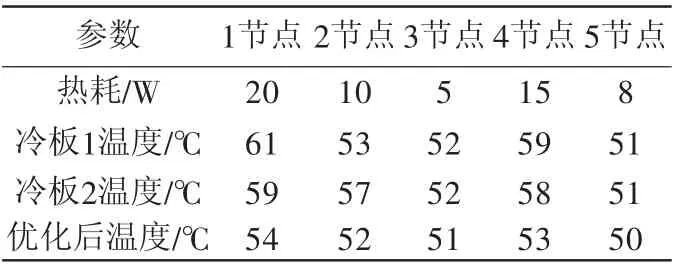
表1 各冷板热源点温度值

4 结语

针对有主散热通道的冷板，采用二维耦合热阻网络建立其热阻模型，对主散热通道上的节点之间的热阻进行了适当等效，在已知冷板边界或内部任一个或多个节点的温度，便可根据热阻网络求出其余所有节点的温度。在此基础上，建立了冷板主散热通道的布局优化模型。采用MATLAB软件编写了求解程序。在程序中调用遗传算法工具箱进行布局优化。该方法适应于对多个散热反案的选择及评估，具有一定的工程实用价值。