五轴机床各轴刚度对S试件的轮廓误差影响的建模仿真

史凤梁，陈秀梅，杨庆东

（北京信息科技大学机电工程学院，北京 100192）

0 引言

为了使机床的加工精度得到进一步提高，首先要完善机床相关性能的检测与评价标准。目前检测机床的加工精度主要通过对机床静态下的各项误差的测量及对机床所加工的标准试件的轮廓误差进行测量来间接反映机床的各项性能。因此国内外相继涌现了许多类型的标准试件，其中成都飞机工业公司立足于航空件的结构而提出的S试件对机床各项性能的反映更为出色[1]。该试件的几何特征复杂，包括不断变化的开角和闭角、连续多变的曲率特性等，这些型面特性使得机床必须要以更复杂的姿态进行加工从而能够很好地暴露出机床加工时的多轴联动性能、刚度特性、摆动轴反向间隙误差等，鉴于此大部分五轴机床在验收时，都选择S试件作为检测试件，在进行机床的精度改良之前一般也以S试件反映的机床性能作为改良基础。

由于经五轴数控机床所加工成型的试件的轮廓误差形成原因复杂，相关学者对S试件误差所反映的机床特性相关方面做了如下研究：霍彦波等[2]利用模型仿真分析了机床各轴的联动误差，尤其是加工S试件不同位置的圆弧时，试件的轮廓误差更能反映五轴机床的平动轴和转动轴的联动性能。分析了五轴加工中心在加工不同位置的圆弧过程中机床平动轴和两个转动轴相互联动时所产生的试件轮廓误差，研究了误差的分布特点并得到了机床各参数和误差间的对应关系。杜丽[3]运用了模糊理论、神经网络等相关方法提出了一种机床动态参数的辨识方法，该方法建立了S试件加工成型后的型面与机床相对应的因素之间的映射关系库，以达到S试件型面轮廓误差的溯源。丁杰雄等[4]通过五轴联动数控机床加工S试件得到了试件型面误差，并对误差进行处理和显示，从而使得误差可视化，方便了对型面误差的分析。本文针对五轴机床的三方向平动轴与两个转动轴建立了其动力学模型，从而得到S试件的轮廓误差模型，通过检测实际加工件验证了模型的正确性，并研究了各轴刚度对轮廓误差的影响。

1 五轴机床各部分动力学模型

1.1 进给系统动力学模型

机床的X、Y、Z三个方向进给系统均为旋转电动机-滚珠丝杠进给系统，为研究进给系统的受力变形，以X轴为例计算各刚度参数，求解系统轴向弹性变形。

本文所研究的五轴加工中心三个平动轴的进给系统所采用的结构均为电动机加滚珠丝杠进给系统，其主要结构如图1所示，包括电动机、联轴器、前支撑轴承、工作台、滚珠丝杠、滚珠丝杠螺母副、后支撑轴承。

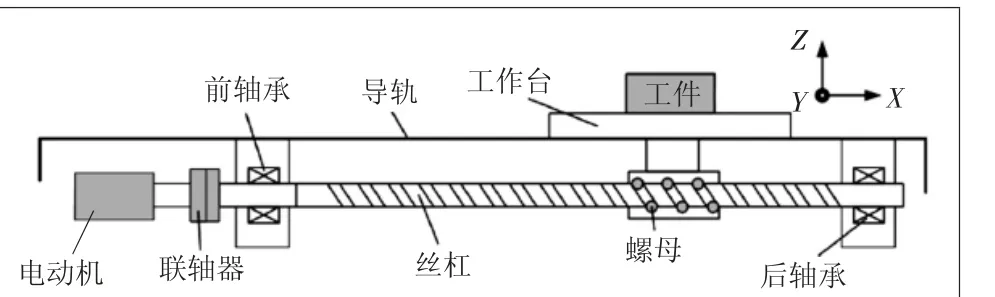
图1 滚珠丝杠进给系统结构

根据进给系统的各部分结构建立进给系统的动力学模型，如图2所示。

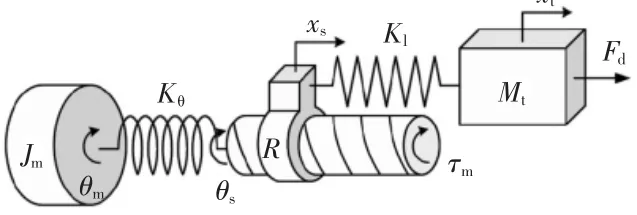
图2 滚珠丝杠动力学模型

设工作台的移动距离为xs，丝杠螺母副的位移为xt，Mt与vt分别为工作台的质量和速度，则有：

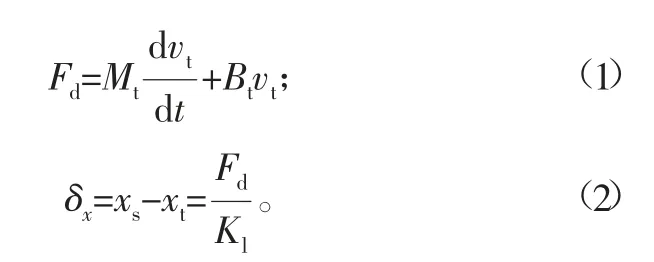
式中：Bt为等效阻尼系数；Kl为进给系统的等效轴向刚度。则有：

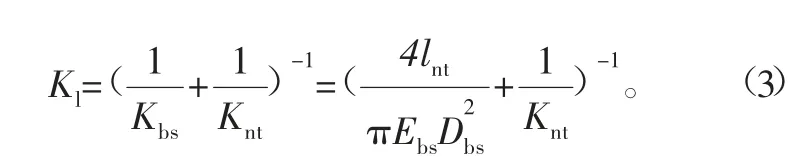
式中：Kbs为滚珠丝杠等效轴向刚度；Knt为螺母副结合面刚度；Ebs为丝杠的弹性模量。

根据式（3）考虑滚珠丝杠轴向结合面的刚度，则有轴向变形为

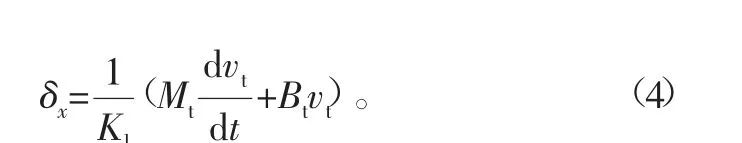
从上式中可以看到，影响滚珠丝杠轴向弹性变形的主要因素有机床的等效刚度、进给系统的速度、加速度及电动机旋转的角速度和角加速度。

由于本文的研究对象的Y、Z方向进给系统采用同样的电动机-滚珠丝杠的结构，所以Y、Z两个方向的进给系统建模与X轴类似。

2.2 BC转台动力学建模

BC轴双转台五轴数控机床的转台模型如图3所示，C轴转台随着B轴的转动而摆动，BC双转台均为力矩电动机直接驱动。以C轴为例，其转台的主要结构为力矩电动机、轴承、静压导轨、编码器及工作台组成，如图4所示。

图3 BC双转台模型

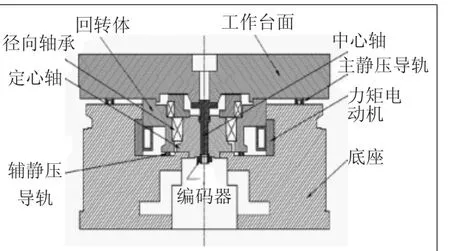
图4 C轴转台结构

以C轴转台为例建立其动力学模型如图5所示。

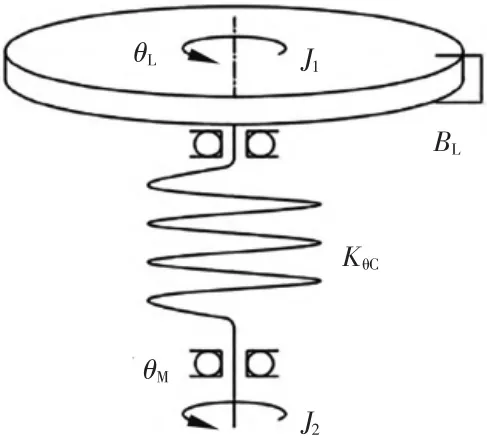
图5 C轴转台动力学模型

设电动机的转动惯量为J1，工作台的转动惯量为J2，KθC表示等效扭转刚度，θM和θL分别表示电动机转角和工作台转角，BL为等效阻尼系数，则它们之间的关系可表示为

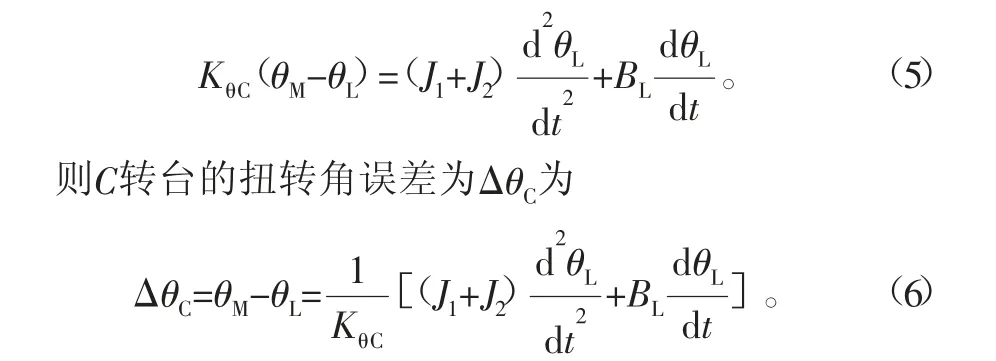
由于B转台与C转台的基本结构相同其轴线方向不同，其动力学建模与C轴类似。

2 S试件的加工仿真

2.1 S试件后置指令的获取

加工仿真S试件首先要对S试件进行粗加工和精加工的路线规划，规划完成之后生成刀位文件，由于刀位文件无法直接让五轴机床进行识别加工，此时需要后置处理生成五轴机床可以识别的NC程序，其中后置处理主要配置机床的结构、机床坐标系、进给速率、刀具等信息。

仿真加工要进行粗、精两道工序的仿真，其中粗加工的目的是铣削掉毛坯多余的部分，并预留出接下来精加工工序的加工余量[5]。精加工工序为机床加工零件的最后一道工序，其加工结果就是机床加工该零件的最后成型结果，相比于粗加工，精加工要求加工后的零件表面质量及轮廓误差都满足要求，精加工仿真所得到的刀路就是后置处理时需要的加工试件刀路，该刀路再经后置处理器处理就能生成可供数控系统识别的NC代码以用于零件加工。仿真参数见表1，得到的粗加工刀路如图6所示，最终得到精加工的刀路如图7所示。

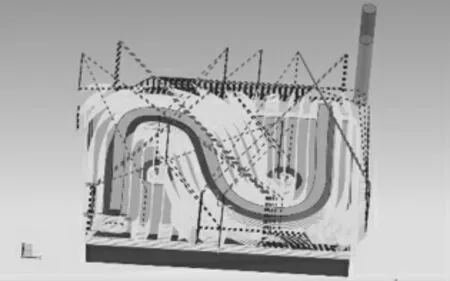
图6 粗加工刀路

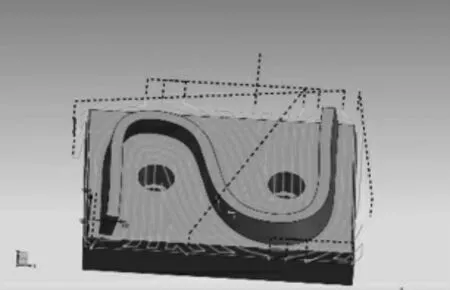
图7 精加工刀路

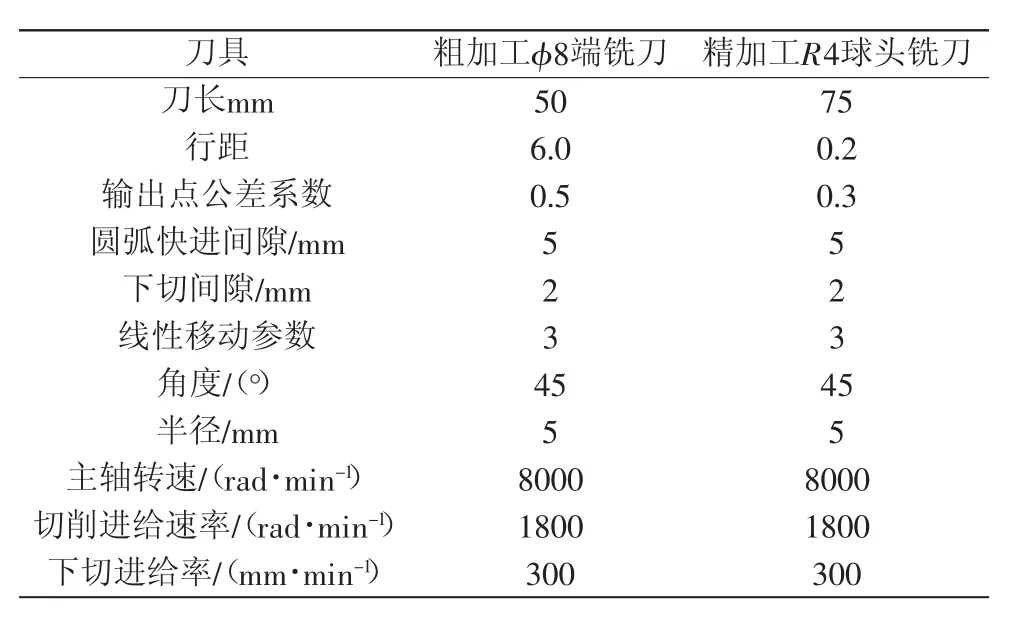
表1 仿真加工参数

上文经过粗加工和精加工的仿真加工得到了试件的刀路，经过后置处理得到可以用于加工的机床NC代码。本文加工S试件所使用的机床为BC双转台五轴机床，其数控系统为SINUMERIK 840D，经过NX的后处理，得到机床加工S试件的精加工的G代码，后置指令为纯文本格式，后置指令中包含着刀具信息、进给速度、运行时间等大量信息，如果要单纯地得到机床在加工过程的刀尖点位置坐标，需要对后置指令进行处理才能得到想要分析的数据。

2.2 数控系统速度求解

五轴联动加工过程中，五轴矢量速度控制时，每组指令点间的时间间隔T可根据编程坐标与编程速度的比值计算，如式（7）所示：

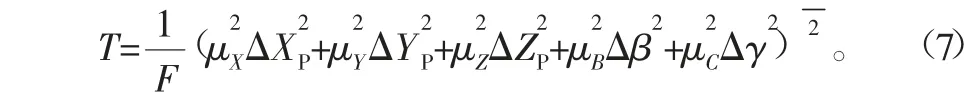
式中：F为编程速度；μX、μY、μZ、μB、μC为长度或角度的标准单位转换为脉冲值的数量值[6]。

各轴的速度可由机床各轴位置的变化量除以时间间隔得到:

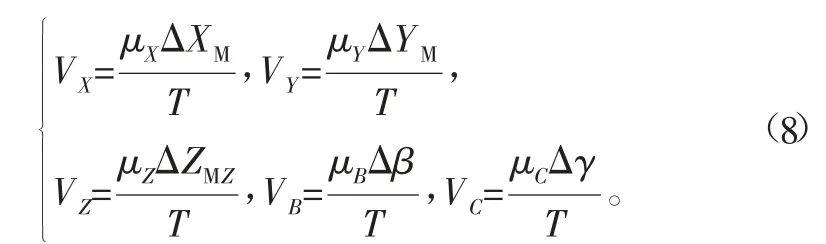
各轴的加速度也可以通过相邻两个坐标点的速度差值除以时间间隔得到。

3 S试件的轮廓误差模型

为了通过机床各轴的弹性变形求得机床刀尖点的偏移误差，必须对五轴加工中心的运动学状态进行求解。

3.1 BC轴双转台五轴机床运动学模型

在机床加工过程中，工件固定于C轴转台上，C轴随着B轴的转动而摆动，B轴在加工过程中其轴线的方向不发生变换，所以B轴为主转动轴也称为定轴，而C轴随着工件的加工，其轴线方向一直发生变换称为次转动轴也称为动轴，在加工过程中动轴的位置受定轴转动状态的影响。所以BC轴双转台五轴数控机床有两条拓扑链，即机床-刀具，机床-工件，该机床的拓扑结构如图8所示。

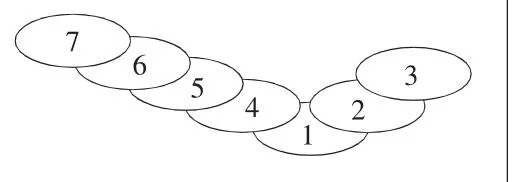
图8 机床拓扑链

由于各轴的变形及主轴弹性变形使得刀尖点的位置发生改变，要得到刀尖点的偏移量大小，首先要根据五轴机床运动学理论将各轴的位移耦合到刀尖点形成刀尖成型轨迹。建立图9所示的坐标系。

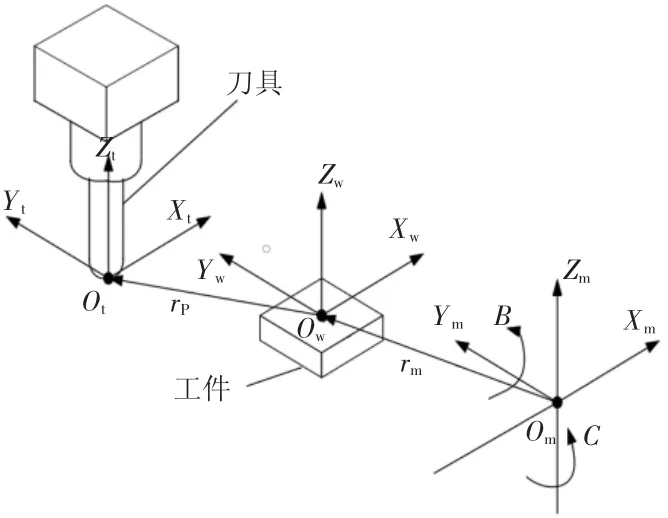
图9 建立坐标系

设参考坐标系原点Om到刀具坐标系原点Ot距离为L，在刀具坐标系中的位置矢量为PM0（XM0，YM0，ZM0）。与初始状态相比，记机床三个直线进给轴的位置坐标为PM（XM，YM，ZM），B轴和C轴转动了角度β和γ（沿X、Y轴的正方向，逆时针转动为正方向）。在工件坐标系下，刀位点的位置矢量和方向矢量分别为P（XP，YP，ZP）和u（iP，jP，kP），其中，XP，YP，ZP分别表示工件坐标系下刀尖点在X、Y、Z三个方向的坐标，iP，jP，kP分别表示在工件坐标系下刀轴姿态在X、Y、Z三个方向的矢量投影。而u（iP，jP，kP）和P（XP，YP，ZP）可由OtXtYtZt相对于OmXmYmZm的平移和OmXmYmZm相对于OwXwYwZw的旋转坐标变换而得到[7]：

3.2 基于后置指令的机床运动状态求解

使用BC轴双转台五轴加工中心仿真加工了S试件，得到了机床的后置指令，通过对加工仿真后置指令的预处理得到机床在加工S试件时，刀尖点的位移轨迹，通过刀尖点的坐标求得各轴的位移。反解式（15）得到机床各轴的位移坐标：

将上节得到的NC代码中的刀尖位置代入式（17）中，解得机床X、Y、Z 三轴加工过程中的位移，图10所示为部分刀位点与三个平动轴之间的关系图。

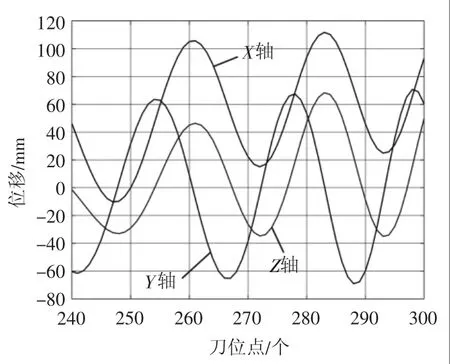
图10 各轴位移

机床的数控系统在加工过程中会按照机床在加工时设定进给速度来给各轴分配运动，当进给速度达不到设定值时，机床数控系统会降低进给速度来保证所加工零件的表面质量。进给速度随着刀路长度的变化如图11所示。

从图11中可以看到，在加工S试件的过程中，设定速度为1800 mm/min，即30 mm/s，机床在加工大部分区域时都没有能够达到设定的进给速度。在刀路长度的中心点位置，速度发生了较大的改变，相应的各轴的加速度也发生较大的改变，其原因是在此处为S试件的一处奇异点，此处机床的C转台运动过一周，相应的各轴位移在这一点附近变化较大。但是由于检测试件时忽略这一奇异点，因此本文也不对此处的影响做以研究。

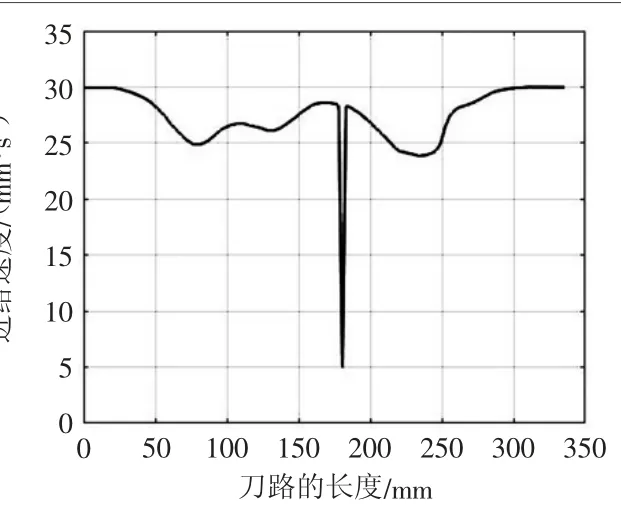
图11 机床进给速度变化

3.3 S试件的轮廓误差

由2.2节可知，刀尖点坐标与三个轴位移的关系表达式，可以得到：

-

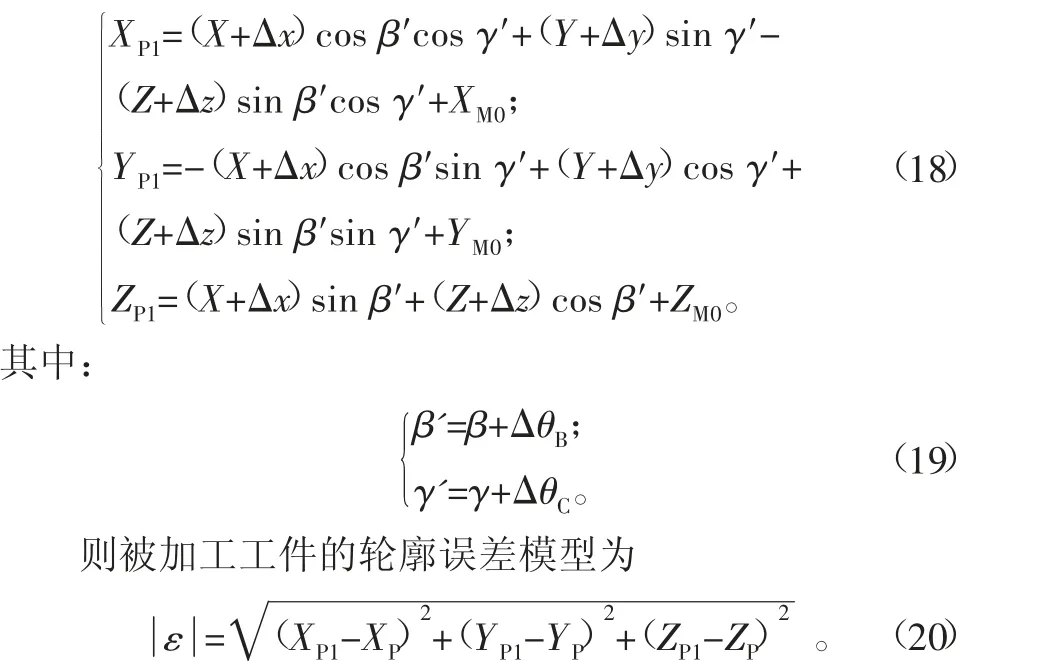
为了得到机床加工S试件时试件的轮廓误差还需要考虑到机床的各项原始几何误差，其部分参数如表2所示。

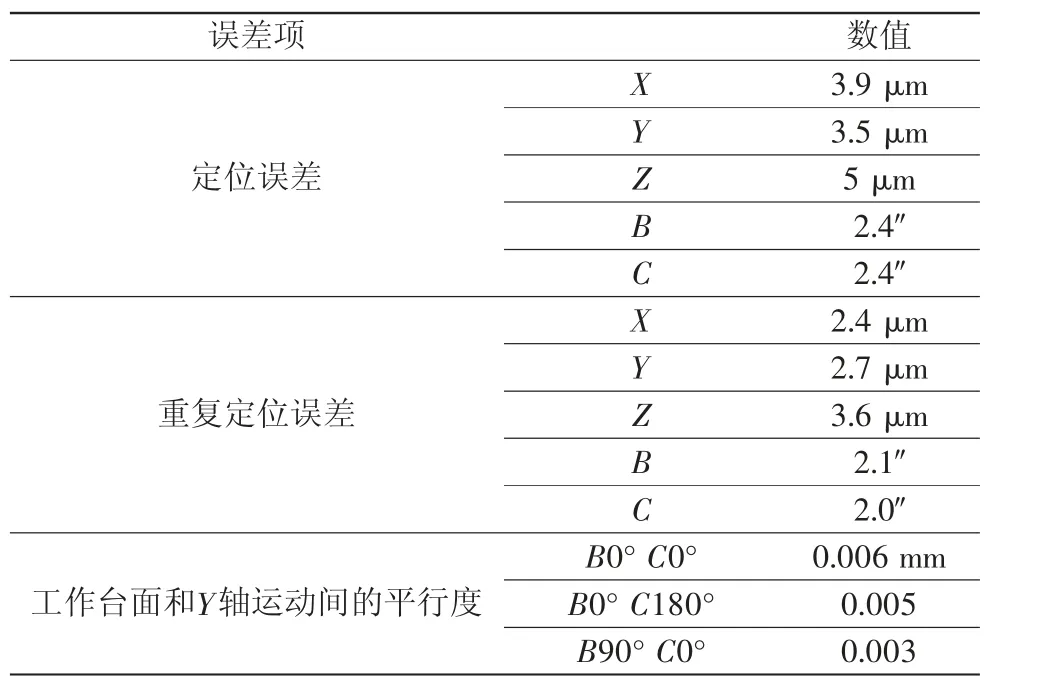
表2 机床几何误差

结合3.2节得到的五轴机床各轴的运动状态参数，一起代入式（18）～式（20）中，得到S试件的轮廓误差模型。

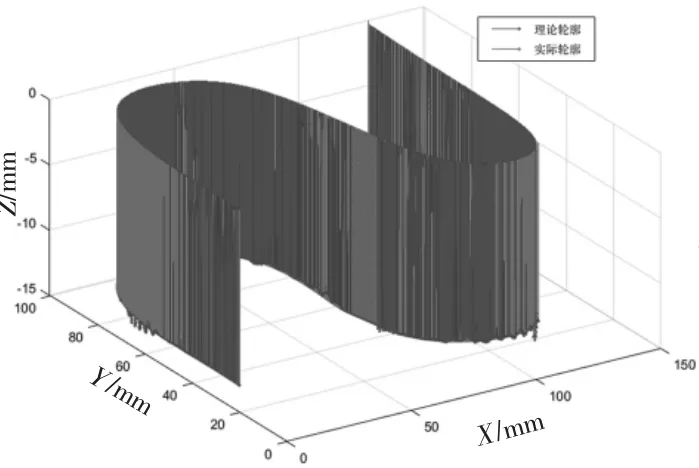
图12 S试件轮廓误差

其中机床的部分参数如表3所示。

表3 机床参数

4 实验对比与各轴刚度影响分析

以本文研究对象BC双转台五轴加工中心为例，以2.1节得到的G代码实际切削加工S试件，如图13所示。

图13 S试件实际加工

将加工后的S试件在三坐标测量仪上进行误差测量，以6 mm高度选取截面，等弧长采样24个点，其采样结果如图14所示。

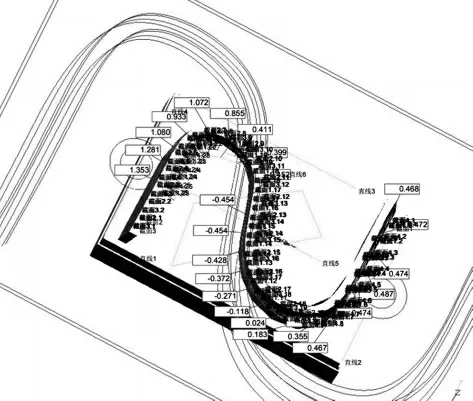
图14 S试件三坐标采样结果示意图

将实际加工测得的S试件轮廓误差与仿真得到的轮廓误差进行对比，如图15所示，可以看到，该模型很好地仿真了S试件加工时的轮廓误差，并且轮廓误差较大的地方为S试件两段曲线部分，其原因是这两个区域曲率变化明显，在加工过程中更易引起机床振动。

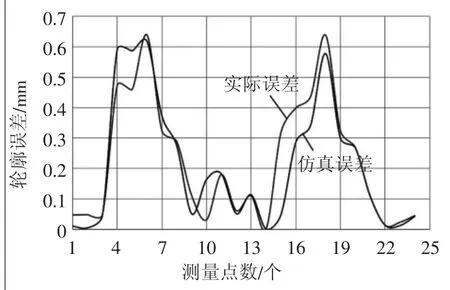
图15 仿真与实际加工误差对比

以该模型为基础，改变模型中的各轴刚度参数，分别得到各轴的刚度对S试件的轮廓误差影响（如图16）。

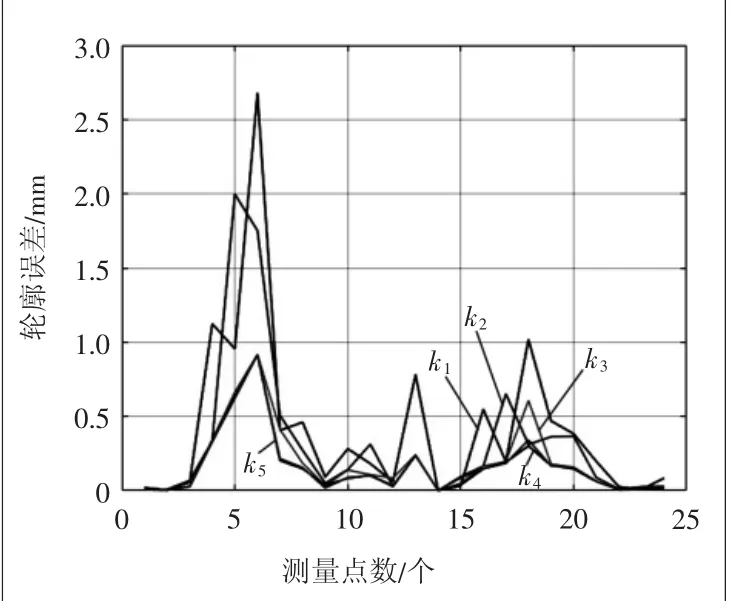
图16 各轴刚度对S 试件轮廓误差的影响

其中k1曲线表示的是X方向等效刚度为600 N/mm，其余各方向的等效刚度为2000 N/mm，以此类推，则k5曲线表示的是C轴的等效扭转刚度为600 N/mm，其余各轴为2000 N/mm。

可以看到，在其他各轴刚性较好时，X方向的进给系统等效刚度系数对S试件的轮廓误差影响较大，Y、Z轴其次，B、C转台的等效扭转刚度对S试件的轮廓误差影响较小且基本相同。

5 结语

本文针对一类BC双转台五轴数控机床建立了其加工S试件的轮廓误差模型，并验证了模型的有效性，在此基础上对各轴刚度参数导致的试件轮廓误差进行分析。

本文建立了三个平动轴与两个转动轴的动力学模型，并仿真加工了S试件，在此基础上综合机床各项原始误差及机床的后置指令得到了S试件的轮廓误差模型，通过与该机床实际加工S试件测得的轮廓误差进行对比，验证了模型的有效性。改变轮廓误差模型的刚度参数，分析了各轴刚度参数对S试件轮廓误差的影响程度，仿真结果表明：在三个平动轴中，X方向的进给系统等效刚度系数对S试件的轮廓误差影响较大，Y轴其次，Z轴影响最小。对比两个转动轴的等效扭转刚度参数，B、C转台的等效扭转刚度对S试件的轮廓误差影响较小。基于以上结论，为此后机床各轴的刚度优化提供基础。