基于指数分布和RAMS 的地铁列车车门可靠性研究

2022-01-22宗志祥

上海工程技术大学学报 2021年3期

宗志祥

（上海地铁维护保障有限公司车辆分公司，上海 200235）

在城市公共交通中，地铁具有准时、载客量大、速度快、安全舒适等优点[1]，成为民众出行的首选.车门系统是地铁列车重要的组成部分，由于地铁站间距短，乘客上下频繁、客流量大，车门系统的高工作强度导致其零部件极易发生故障[2].因此，对地铁车门故障的分析诊断逐渐成为研究热点.

近年来，国内学者对地铁车门故障进行了大量研究.詹文元[3]对深圳地铁1 号线车门控制器故障进行分析，提出相应的整改措施，有效控制了车门控制器故障.丁心凡[4]分析车门非站台侧开门故障的原因，认为开门控制电路存在设计缺陷，针对缺陷整改后彻底消除了非站台侧开门故障隐患.赵伟龙[5]对广州地铁3 号线所有地铁车门进行大修，发现车门系统整体故障率降低约20%，提高了车门系统的可靠性.陈卓群等[6]针对车门紧急解锁故障提出两种解决方案，通过对比确定车辆控制系统旁路改造更具经济性和实用性.现有研究都是针对地铁车门的子系统或者车门系统某个部件引起的故障进行分析和处理来提高地铁车门的安全可靠性，但大多研究都只是分析故障本身，缺少对车门故障统计数据深入挖掘，无法对车门故障的发展做出预判，达到预防和减少车门故障的目的.

为此，根据上海地铁13 号线路3 年车门故障统计数据，利用指数分布函数对其进行描述，结合RAMS 中的可靠性理论，分析3 年车门的可靠性，以列车车门综合可靠度为目标，提出确定车门预防性检修周期的方法.

1 车门故障部件组成

故障是产品或产品的一部分不能或将不能完成预定功能的事件或状态[7].由于地铁车门系统非常复杂，集电控和机械传动于一体[8]，其车门故障主要由客室车门机械部件、客室车门电气部件、司机室侧门、通道门和紧急逃生门等部件引起，其各部件的组成如图1 所示.

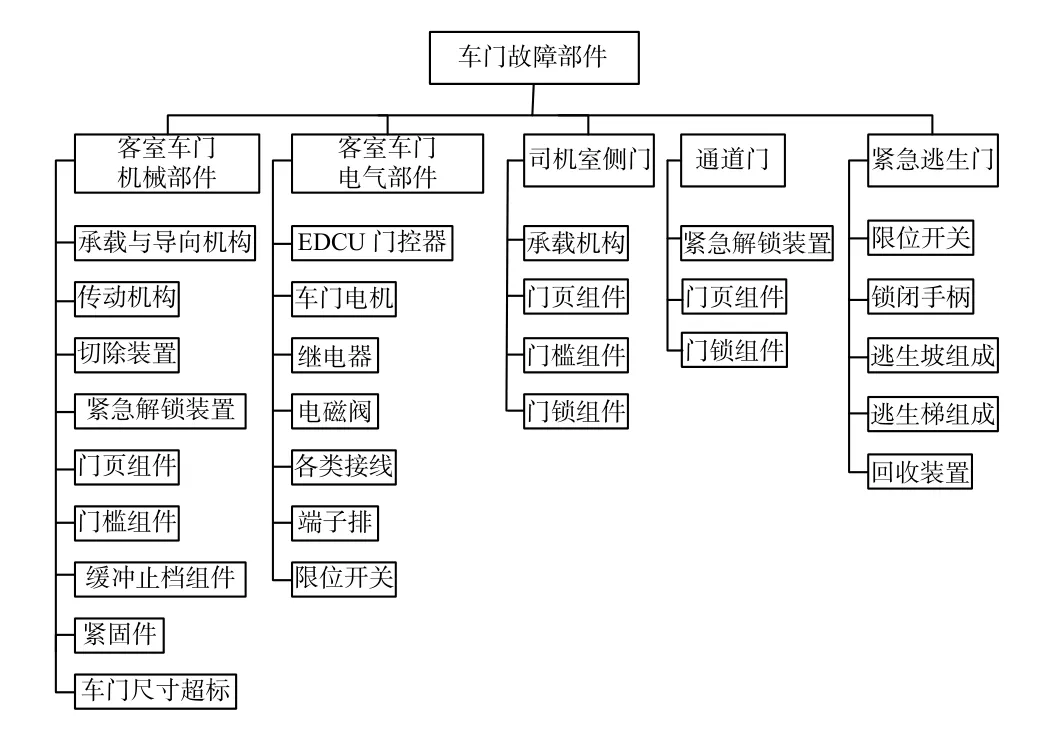
图1 车门故障部件组成图Fig.1 Composition diagram of door failure parts

2 车门故障时间间隔分布规律

2.1 指数分布

上海地铁车门系统的检修记录数据包括正线车门故障记录和班组检修记录.由于正线车门故障会对乘客的人身安全和运营稳定性造成巨大威胁[9]，因此根据上海地铁13 号线路2016—2018 年正线车门故障检修记录数据，利用概率统计方法对车门故障时间间隔进行描述.选用指数分布对车门故障时间间隔样本进行推断，令车门时间间隔为随机变量X，其概率密度函数为[10]

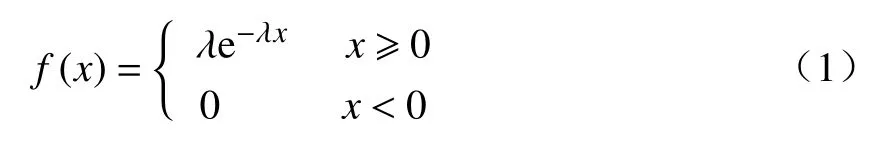
式中：λ为率参数，即每单位时间内发生某事件的次数.X服从以 λ为参数的指数分布，记为X∼E(λ).其指数分布函数可表示为

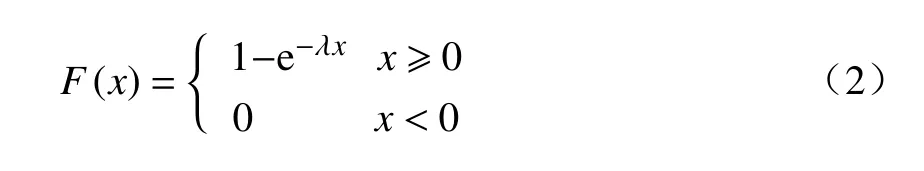
利用式(1)、式(2)获得3 年车门故障时间间隔值的分布拟合，如图2 所示.

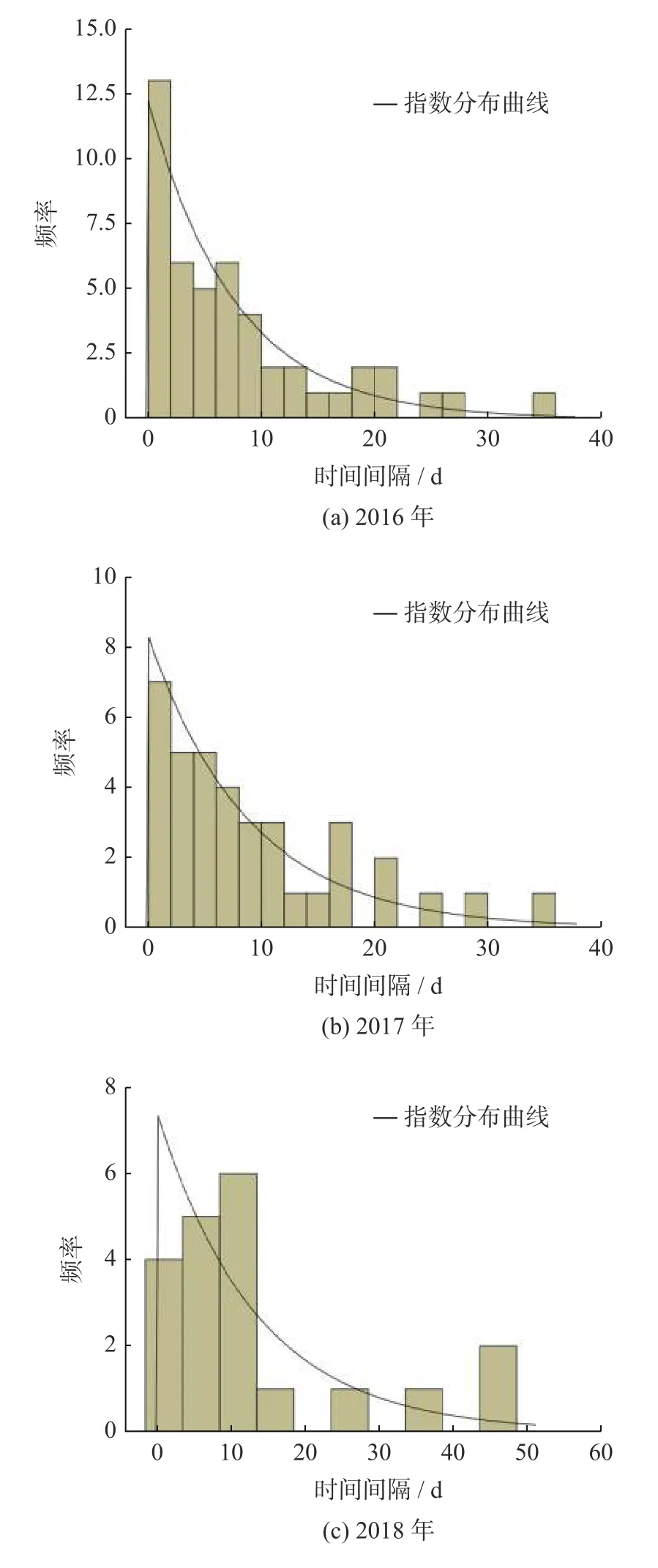
图2 车门故障时间间隔指数分布拟合曲线图Fig.2 Fitting curve diagram of door failure time interval exponential distribution

2.2 假设检验

对地铁车门故障时间间隔总体样本服从指数分布的推断进行假设性检验，验证其假设的正确性，具体步骤如下.

1）提出零假设和备择假设

零假设H0：X服从指数分布.

备择假设H1：X不服从指数分布.

2）选择指数分布检验方法

选用非参数检验K–S检验(Kolmogorov-Smirnov Test)对样本数值进行检验.

3）选择显著性水平α

显著性水平通常取值0.01、0.05、0.1，本研究中，取显著性水平 α=0.05.

4）计算检p值

检验的p值是指在零假设条件成立下，检验统计量等于现实值的概率.p值越小，说明在零假设的前提下发生小概率事件，应该拒绝零假设.

5）检验判断

比较p值和α值的大小，若p<α，则拒绝零假设；若p>α，则不能拒绝零假设，说明X服从指数分布.

根据以上步骤，获得上海地铁13 号线全部列车的车门故障时间间隔假设性检验，见表1.

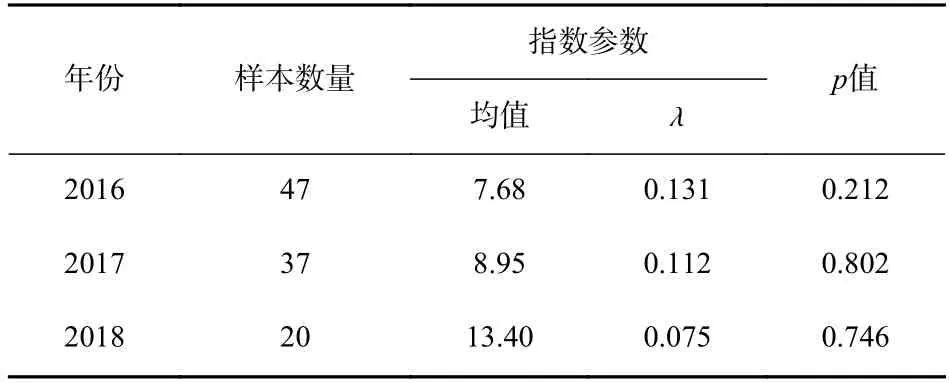
表1 车门故障时间间隔假设性检验Table 1 Hypothesis test of door failure time interval

由图2 和表1 可知，3 年车门故障时间间隔的假设性检验的p值分别为0.212、0.802、0.746，大于设定的显著性水平0.05，这意味着不能拒绝零假设，因此，3 年车门故障时间间隔都服从指数分布，分别记为：X2016∼E(7.68)、X2017∼E(8.95)、X2018∼E(13.40).

3 车门可靠性分析

RAMS是可靠性(Reliability)、可用性(Aviliailabty)、可维护性(Maintainability)和安全性(Safety) 4 个词的英文首字母缩写.其中，可靠性是指产品在规定条件下和规定时间内完成规定功能的能力，与可靠性相反，产品丧失规定的功能称为失效或故障.RAMS 中用来衡量产品可靠性的指标主要有失效率 λ、平均故障间隔时间MTBF和可靠度R.因为系统或部件的失效时间是随机的，将失效时间作为变量，可用一个恰当的函数去描述，找出系统和部件故障分布规律，进一步分析和预测故障的发生并制定维修策略，从而提高系统或部件的可靠性.

为减少和预防车门故障的发生，结合3 年车门故障时间间隔分布规律，利用RAMS 中可靠性理论对车门进行可靠性分析.

1）失效概率密度函数

车门故障间隔时间服从指数分布时，其失效概率密度函数f(t)可表示为

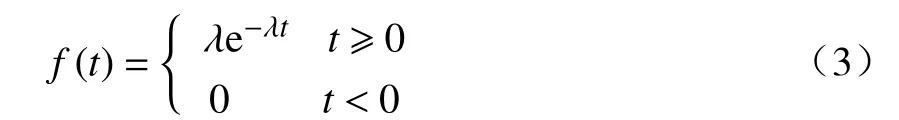
式中：λ为指数分布的失效率，为常数.

根据式(3)可获得3 年车门失效概率密度函数图像，如图3 所示.

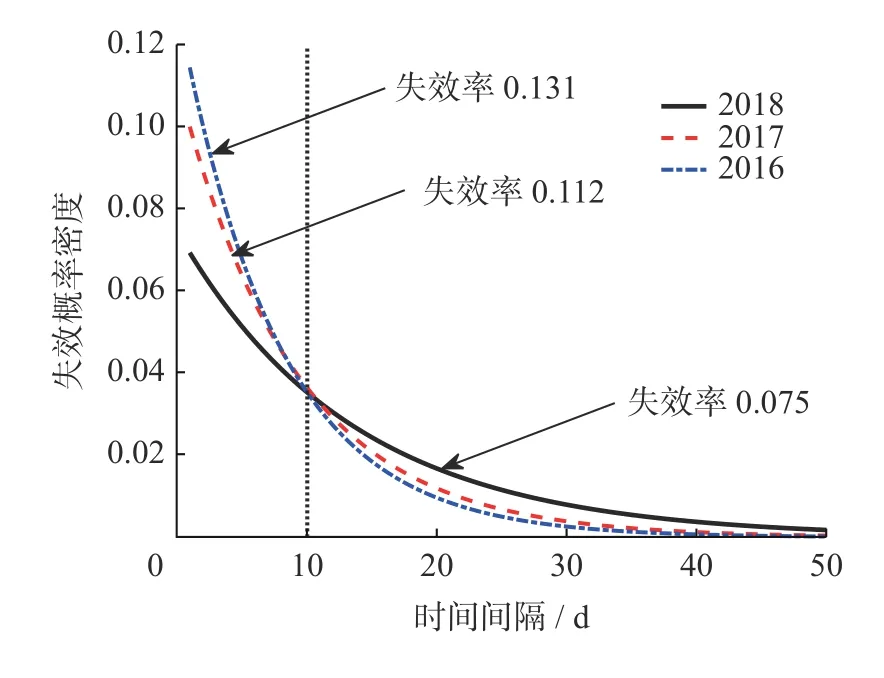
图3 车门失效概率密度函数图Fig.3 Door failure probability density function graph

由图3 可知，3 年的失效概率密度都呈下降趋势，这说明车门故障间隔时间分布在有限的时间内，且随着时间间隔的增大，其分布越来越少.此外，失效率越大，初始的概率密度越大，其失效概率密度下降速率越大.这说明失效概率越大，车门更容易发生故障，且车门故障时间间隔主要分布在较小的时间段内.

2）平均故障间隔时间

当车门故障间隔时间服从指数分布时，MTBF可以表示为

鉴于车门故障间隔时间服从指数分布时，利用式(4)可计算获得3 年的车门平均故障间隔时间，见表2.

表2 车门平均故障间隔时间Table 2 Mean time between door failures

由表2 可知，相较于2016 年和2017 年的平均故障间隔时间，2018 的平均故障间隔时间最大，这说明车门能够持续工作的时间更长，能够为列车赢得更多的日常检修时间，从而减小正线列车发生故障的概率，这也间接说明2018 年车门可靠性高于2016 年和2017 年，不易发生车门故障.

3）可靠度

当车门故障间隔时间服从指数分布时，其可靠度函数R(t)可表示为

利用式(5)获得3 年车门可靠度如图4 所示.由图4 可知，2018 年车门可靠度一直高于2016 年和2017 年，这说明失效率越小，可靠度越高.此外，对同一可靠度，2018 年的车门故障间隔时间大于2016 年和2017 年，这说明2018 年车门工作时间要长于其他两年.因此，可认为2018 年车门的可靠性更高.

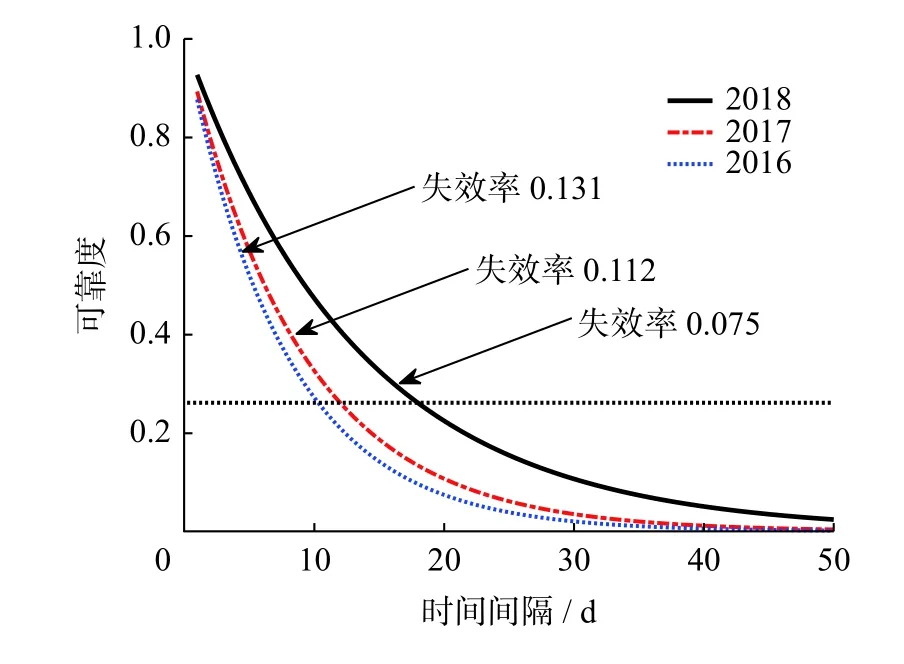
图4 车门可靠度图Fig.4 Door reliability diagram

4 检修周期研究

地铁车门在正线运营时间段内，需要保证其可靠性.在这个前提下，需要解决的问题是如何确定合理的预防性检修周期，并且在这个预防性检修周期内，部件虽不能一直保持高可靠度，但也不会失效.以车门综合可靠度为目标，结合地铁车门每年的故障检修数据，获得车门预防性检修周期.

以可靠度为目标的车门预防性检修周期T0的表达式为

式中：R0(T0)为地铁正线运行在T0时间段内不发生故障而要求车门达到的可靠度要求值；Rd(T0/T)为要求车门在T时间段内不发生失效，即不更换零部件，车门在正线工作T0时间段内不发生故障时达到的可靠度要求值，即条件可靠度，公式为

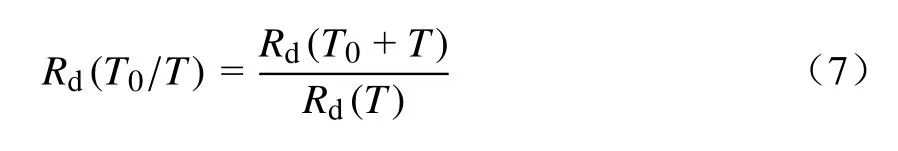
在地铁车门系统的均衡检修项目中，由于检修项目众多且每个项目的可靠度要求各不相同，取每列车的综合可靠度分别为0.90、0.95、0.99.以2018 年检修周期为例，在不同可靠度下，根据式(6)、式(7)可获得列车车门动态预防性检修周期，见表3.

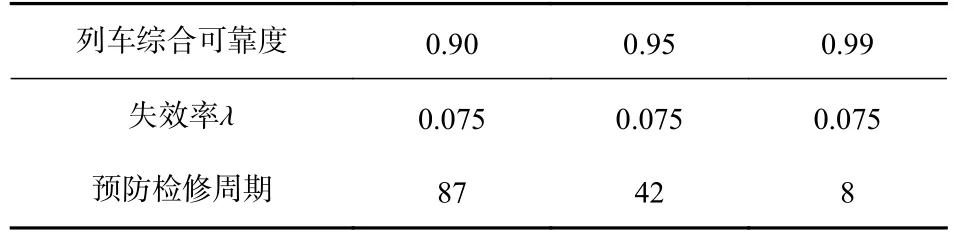
表3 不同可靠度下的车门预防性检修周期Table 3 Preventive maintenance cycle of door under different reliability

从表3 可以看出，列车综合可靠度越高，其预防检修周期也越短，这意味着维修花费越高，而且过短的维修周期会造成经济浪费和车门部件破损.因此，需要根据供应商的维护手册确定列车综合可靠度以及线路的地铁车辆，确定列车车门预防性检修周期.

综上，获得列车车门预防性检修周期的流程为：第1 步利用概率统计方法对地铁车门故障时间间隔进行描述；第2 步选用检验方法对提出的统计推断进行假设检验，服从指数分布则可进行下一步，不服从指数分布则事件结束；第3 步利用RAMS的可靠性理论，以可靠度为目标，结合地铁列车的数量和地铁列车的实际可靠度要求获得列车车辆车门预防性检修周期.流程图如图5 所示.