随机低秩逼近算法在推荐系统中的应用

陈 熙，邓杰臣，席势鸿，刘晓辰，张相君，冯月华

（上海工程技术大学 a.机械与汽车工程学院；b.航空运输学院（飞行学院）；c.数理与统计学院，上海 201620）

随着信息技术的发展，人们能获取的信息越来越多，但从这些庞大的信息中寻找出自己所感兴趣的信息比较困难，而推荐系统可以通过搜集不同用户的信息需求来自动预测出用户可能需要的信息，并将这些信息推送给用户.目前，推荐系统广泛应用于各种领域，如电影、音乐、新闻、书籍、研究文章、搜索查询、金融服务、人寿保险等[1].

推荐系统中一个典型是Netflix 推荐系统[2].Netflix 是一家提供电影租赁服务的公司，拥有超过两千万的用户群，每位用户都可依据自己的感受对观赏过的电影进行1～5 分的评价.由于影片数目众多，影评人不可能将每部影片都看完才评出分值.相对于整个数表构成的矩阵，已知分值对应的元素个数很少，而且通常仅有很少的几个因素能够影响和决定用户对某部电影的评价，从而矩阵可以看作是低秩的，矩阵填充理论为这个数表的未知元素的精确填充提供了可行途径[3].

针对矩阵填充问题，国内外众多学者提出诸多求解此问题的算法，如奇异值阈值算法(SVT)、固定点连续算法(FPC)、不精确的增广Lagrange乘子法(IALM)等[3−4].这些算法中最为复杂的部分是计算奇异值分解(Singular Value Decomposition，SVD)，并且IALM 被证明是这些算法中最精确和有效的算法.对于SVD 的计算，古典方法为LANSVD 算法[5]，但该方法在数据量很大时效率较低.Drineas 等[6]提出线性时间的SVD 方法，此方法虽然在效率上有很大提升，但其精度差[4].此外，计算SVD 的方法还有随机SVD，带有子空间迭代的随机SVD、TUXV、FFSRQR 算法等[4,7]，由于这些方法需要多次访问原始数据，因此在数据量特别大的情形下其效率有待改进.

为提高求解矩阵填充问题的效率，本研究基于随机算法策略，高效数据访问的要求并结合IALM 算法，提出一种新的高效算法求解矩阵填充问题，并用Matlab 软件实现该算法.

1 随机算法

任意给定一个矩阵A∈Rm×n，其奇异值分解(SVD)是将A分 解成3 个矩阵的乘积，即A=UΣV.其中，U=(u1,u2,···um)∈Rm×m和V=(v1,v2,···vn)∈Rn×n为正交矩阵，对角矩阵Σ ∈Rm×n的对角元满足σ1≥σ2≥···≥σm≥0.在大数据分析和机器学习中，SVD 已成为一种关键的分析工具[4].

随着大数据时代到来，SVD 和QR 等经典的高内存消耗和高计算复杂度的算法已经无法满足时代发展需求.近年来随机算法的发展为构造近似SVD 算法提供一个强大的工具.与古典确定性的数值算法比较，随机算法简单而有效，运行效率更高，更具鲁棒性，使用内存空间更少.Tropp 等[7]基于列随机采样提出了单步随机奇异值分解(SPRSVD)算法计算给定矩阵的近似SVD，具体内容见算法1.其中，符号“†”表示矩阵的广义逆.该算法只在最开始时用到原始数据集，因此具有高效的数据访问能力.

算法1 SPRSVD 算法

输入：矩阵A∈Rm×n，目标秩k，过采样参数p≥0，整数l≥(k+p).输出：

包含矩阵A的前k个近似左奇异向量的列正交矩阵U∈Rm×k；

包含矩阵A的前k个近似奇异值的对角矩阵Σ ∈Rk×k；

包含矩阵A的前k个近似右奇异向量的列正交矩阵V∈Rn×k.过程：

生成两个一致独立同分布的高斯矩阵Ω1∈

计算Y=AΩ1,W=Ω2A；

计算Y的正交矩阵Q:Q=orth(Y)；

计算B=(Ω2Q)†W；

计算B的奇异值分解:[U,Σ,V]=svd(B)；

计算U=Q∗U；

计算U=U(:,1:k),Σ=Σ(1:k,1:k),V=V(:,1:k).

2 矩阵填充问题

矩阵填充问题的基本内容是通过少量观测值来恢复整个矩阵，核心是一个在随机约束下的仿射秩最小问题:

式中：M为待恢复的原始矩阵；Ω为均匀随机采样集.由于求解此类问题是NP 难问题，目前主流思想是将该模型转化为核范数最小问题，表达式为

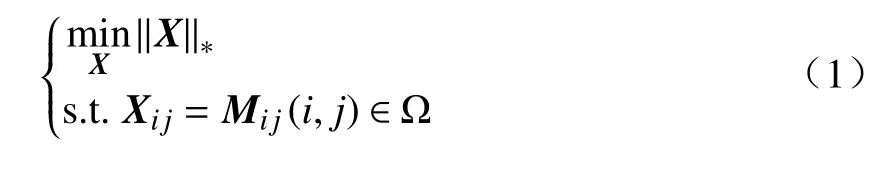
式中：∥X∥∗为核范数，表示X的奇异值之和.矩阵填充问题式(1)可以改写为

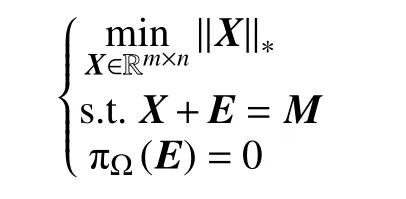
式中：πΩ:Rm×n→Rm×n为一个正交投影算子，它使在 Ω内的元素不发生改变，而在 Ω外的元素为零.在文献[8]中，作者应用IALM 算法求解上述问题，具体见算法2.在算法2 中，Sω(x)=sgn(x)·max(|x|−ω,0)是一个软收缩算子且x∈Rn,ω>0，为 Ω的补集.

算法2 IALM 算法

输入：原始矩阵M，采样数据集 Ω，采样元素πΩ(M)，正数λ,µ0,精度 tol，ρ>1.

输出：

矩阵对(Xk,Ek).

过程：

k=0,Y0=0,E0=0；

当算法不收敛时，开始循环操作：

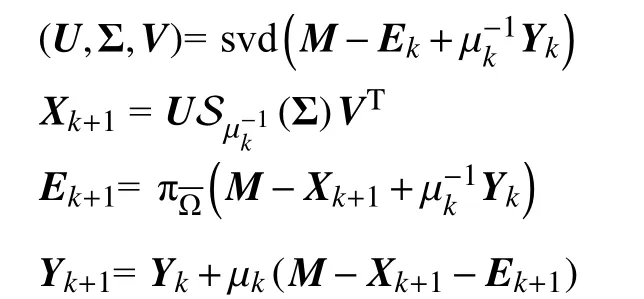
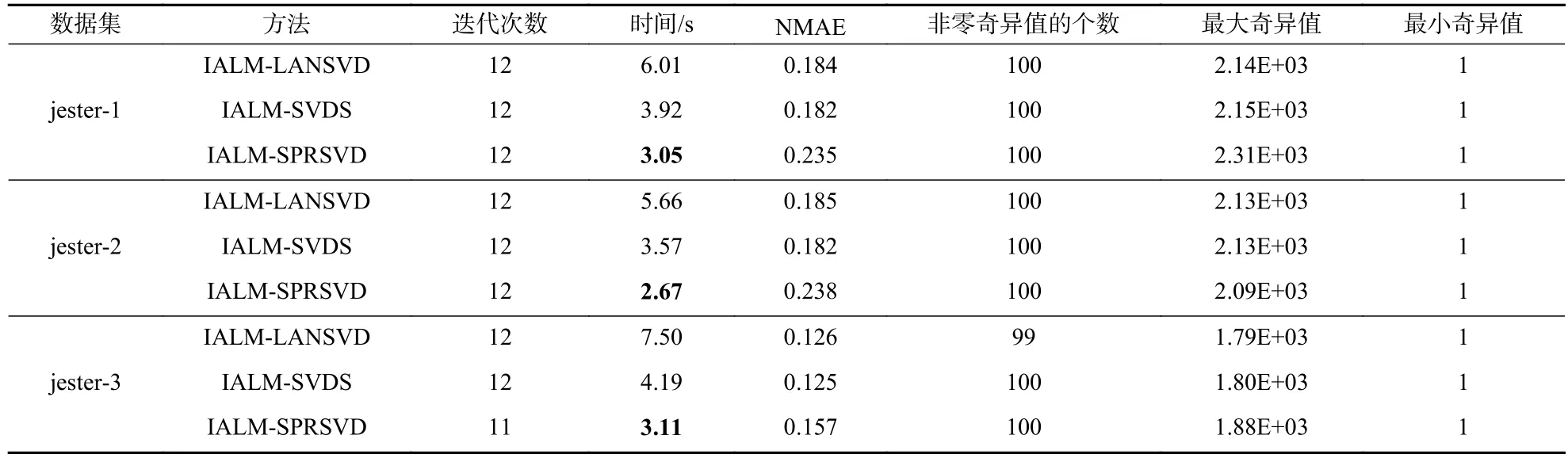
更新µk+1=，k=k+1，当∥M−Xk−Ek∥F/∥M∥F

3 新算法IALM-SPRSVD

在大数据环境中，数据集越来越大，对算法的效率要求也越高.算法2 中计算代价最大的是循环中计算SVD，因此本节将用SPRSVD 取代算法2 中的SVD，得到更高效的求解矩阵填充问题的算法，并将此算法命名为IALM-SPRSVD，具体见算法3.

算法3 IALM-SPRSVD 算法

输入：原始矩阵M，采样数据集 Ω，采样元素πΩ(M)，正数λ,µ0,，精度 tol，ρ>1.目标秩kr=5，过采样参数p=5.

输出：

矩阵对(Xk,Ek).

过程：

k=0,Y0=0,E0=0；

当算法不收敛时，开始循环操作：

更新µk+1=k=k+1，当∥M−Xk−Ek∥F/

4 数值试验

在本节中，通过几个数值试验验证新算法IALM-SPRSVD，并与LANSVD 以及Matlab 自带的svds 命令进行比较.针对IALM 算法中需要计算SVD 的步骤分别用LANSVD、SVDS 和SPRSVD方法，对应的算法分别命名为IALM-LANSVD、IALM-SVDS 和IALM-SPRSVD.所有试验都是在一台拥有2.9 GHz Intel Core i5 处理器和8Gb RAM的笔记本电脑上进行的.本研究选取Jester Joke 数据集来完成数值实验，该数据集可以在Jester 网站下载.Jester Joke 数据集由73,421 个用户针对100 个笑话产生的410 万个评分组成，具体包括以下3 个子集.

jester-1:数据来自24 983个用户，他们对36个或更多的笑话进行了评级；

jester-2:数据来自23 500个用户，他们对36个或更多的笑话评分；

jester-3:数据来自24 938个用户，他们对15～35个笑话评分.

对于每个数据集，令M为原始数据矩阵，其中Mij为用户i对第j个笑话的评分；Γ为Mij中已知元素的索引集.采用归一化平均绝对误差(NMAE)来衡量矩阵填充算法的质量，公式为

式中：Xij为用户i对笑话j的预测评分；rmax、rmin分别为评分的上界和下界.在试验过程中，令rmax=10，rmin=−10，结果见表1.

表1 矩阵填充问题的比较Table 1 Comparison of matrix completion problems

从结果观察到，对于这3 个数据集IALMSPRSVD 实现了与其他方法几乎相同的可恢复性，并且效率比IALM-LANSVD 提高了两倍左右，与IALM-SVDS 相比，提高程度也接近30%.

5 结语

本研究基于随机算法提出了IALM-SPRSVD算法，改进了原有IALM 算法在求解矩阵填充问题上的效率.由于实际的数据集通常具有稀疏性，本研究将在现有研究基础上，在后续工作中研究适应数据集稀疏性的算法.