代数恒等变形在代数求值中的应用

江西省临川二中 (344100) 黄卫民

数学解题就是一系列连续的化归、变形与转化，把未知的、陌生的转化为已知的、熟悉的，把复杂的情形变形为简单的情形．变形应当具备一定的目的性、方向性和针对性，往目标进行有目的地变形，有利于形成有效的有序逻辑推理，本文以代数条件恒等式为例，谈谈如何在代数恒等式变形里实施有序逻辑推理．

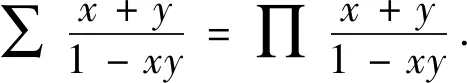
本题见文[1]的第52页，原作者是用三角换元证明的，其实可以直接给出证明．

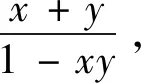
例2 已知a(y+z)=x,b(z+x)=y,c(x+y)=z，求证：∑ab+2abc=1．

本题见文[2]的第13页，可用分离变元，消元等方法来证明．

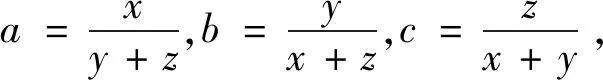
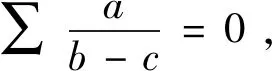
本题是文[3]中第210页的一道习题．

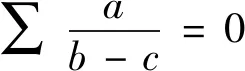
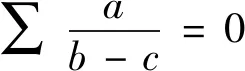
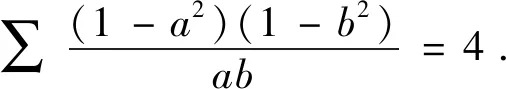
该问题常规的解题方法为三角换元法，见文，但本题还可通过代数恒等变形来处理．

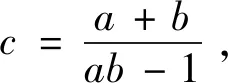
点评：本题的证明利用了题设条件和证明目标均为轮换对称式，将同种类型的代数式结合在一起，构成新的轮换对称式，通过合理的变形，达到快速解题的目的．

例5 已知a2+b2=1，c2+d2=1，ac+bd=0，求证：a2+c2=1，b2+d2=1，ab+cd=0．

本题为一道经典的代数恒等变形求值题，出自文的第175页．

证明：由于a2+b2=1，c2+d2=1，ac+bd=0，则0=(a2+b2-1)2+(c2+d2-1)2+2(ac+bd)2=(a4+b4+1+2a2b2-2a2-2b2)+(c4+d4+1+2c2d2-2c2-2d2)+2(a2c2+b2d2+2abcd)=(a4+c4+1+2a2c2-2a2-2c2)+(b4+d4+1+2b2d2-2b2-2d2)+2(a2b2+c2d2+2abcd)=(a2+c2-1)2+(b2+d2-1)2+2(ab+cd)2因此a2+c2=1，b2+d2=1，ab+cd=0．

点评：本证明是从条件出发，构造非负关系式，再通过配方的技巧，构造新的非负关系式，对问题进行例整体处理，体现了从分到合、再到分的数学思想方法．

解题的过程就是对数学关系式实施变形和转化的过程．对参变元的消元，可以起到减少变元的作用，达到“化多为少”、“化复为简”的效果．解题的目标意识，减少和消除差异，消元变更，对轮换对称式进行合理地拆分和合并都是实现代数恒等变形的有效逻辑．