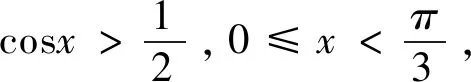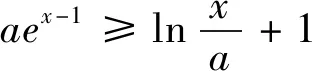例谈解题教学中数形结合思想方法的渗透
2022-01-22福建省莆田第四中学351100罗梦柱
福建省莆田第四中学 (351100) 罗梦柱
知识是载体,方法是手段,思想是灵魂,它们是知识体系的三个层次.在日常教学中,教师往往注重知识的讲解,方法的传授,却将数学思想的渗透丢弃一边.为什么很多学生数学的学习仅仅停留在最初级的模仿阶段?题目变一下,就不会了呢?究其原因,绝大多数学生是不懂得站在思想的高度来思考和引领方法,或者是由于思维混乱导致想不起来用什么方法来求解数学问题.因此,教师在讲解知识和传授方法的同时,进行数学思想方法的渗透,能够帮助学生站在更高的层次思考问题,更有利于学生能力的提升.
数形结合思想体现了数学是研究数量关系和空间形式的科学的本质,利用数形结合思想引领数学解题,有利于分析题中图形与数量之间的内在联系,启发学生思维,帮助学生快速寻得问题求解的方向.本文以多个典型例题为例,从以“数”化“形”、以“形”变“数”、“形”“数”互变三个方面阐述在教学中渗透数形结合思想对于数学解题的深刻意义.
1、以“数”化“形”,将抽象问题直观化
高中数学中数量关系占据着重要的地位,对数量关系进行分析可以锻炼学生的逻辑思维能力,而这正是教学的一大难点.为了突破这个难点,在教学过程中,教师要有意识的引导学生借助几何图形将题设条件直观化,通过图形反映出来的数量关系,找到数与式的本质.
分析:本题若从代数的角度去求解,势必异常繁琐,违背了命题者的命题意图,在教学中可尝试引导学生通过建立平面直角坐标系,将“数”化“形”,通过图形反映出的数量关系,能够将问题轻松解决.
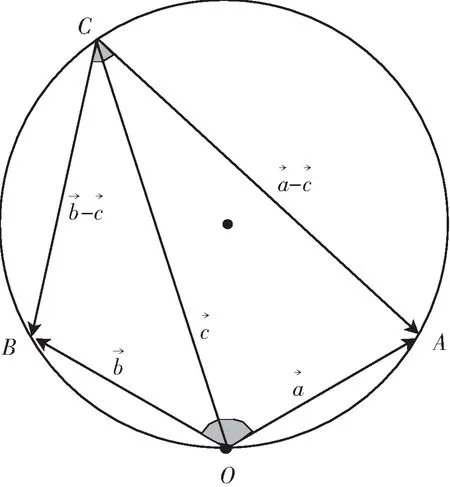
图1
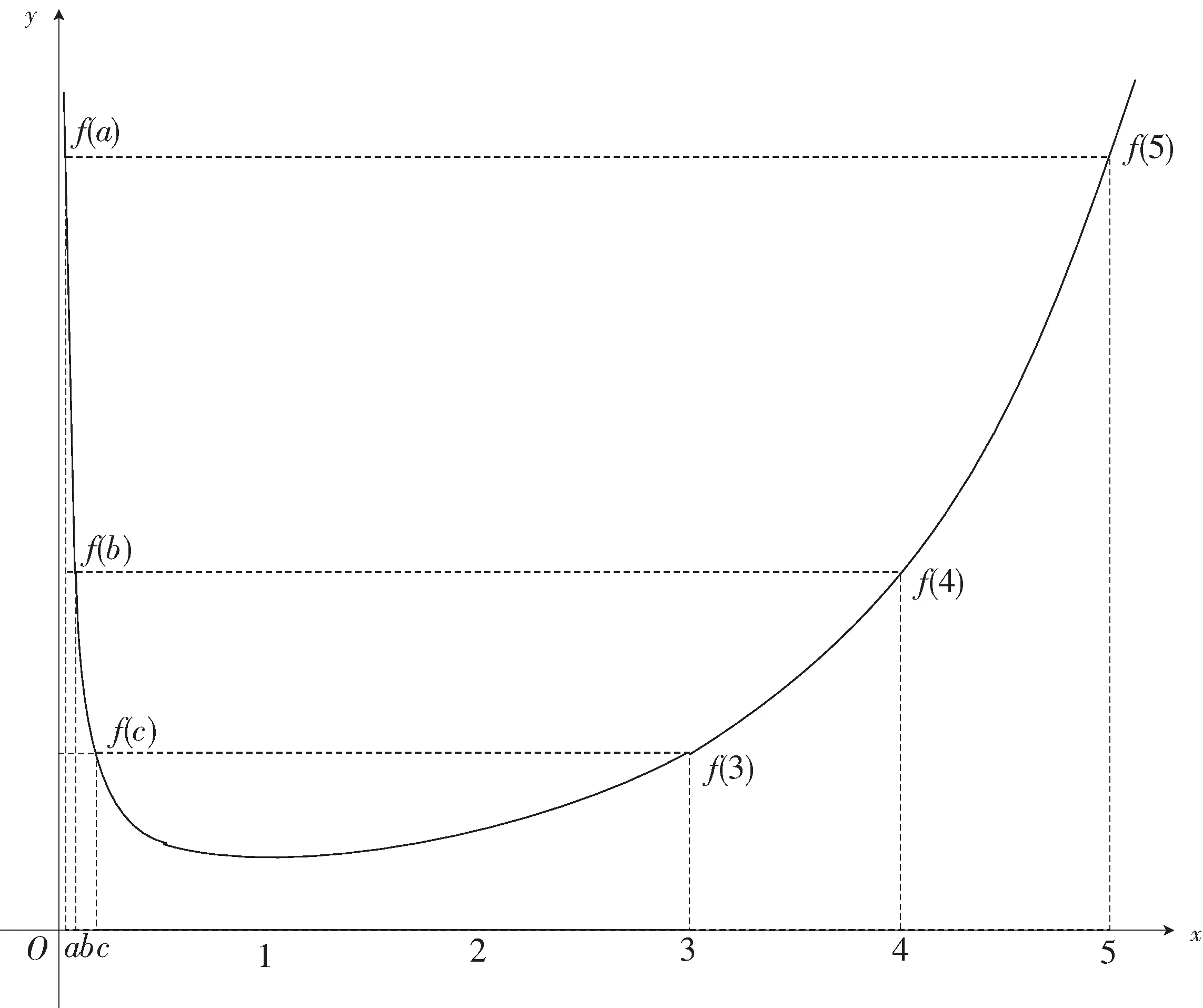
例2 (2021年八省适应性考试第8题)已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则( ).
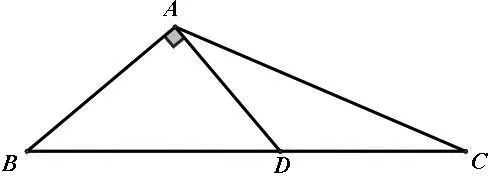
A.c C.a 结合f(x)的图像如图2,0 图2 分析:破解圆锥曲线问题往往需要根据题目所涉及图形的几何性质,从“几何角度”入手,利用图形反映出的数量关系,可以更简便地求解出问题,更彰显问题本质. “形”具有直观的特点,可以将一些抽象的思维直观地表现出来,然而在量方面,却存在一定的不足,还需要借助“数”进行计算,尤其是在一些比较复杂的图形中,由于直接观察不能得到结论,这时就需要从“形”出发,转化为对应形式的“数”,借助数量解决图形问题,这种“形”变“数”的模式,可以将不容易计算的问题变得易于计算,进而快速解决图形问题. 图4 分析:单纯依赖图形,无法准确刻画边、角之间的关联,利用AD⊥AB,建立平面直角坐标系,通过坐标运算,能够更直观、更快速地求解问题. 图5 图6 分析:从“形”的角度,本题无法直接求解,需要将“形”变为“数”,通过“数”的运算,揭示各种量的内在关联,达到问题求解的目的. 图7 数学家华罗庚曾说过:“数缺形时少直觉,形少数时难入微.”这句话深刻地揭示了数形之间的辩证关系以及数形结合的重要性[3].对于一些较复杂的数学问题,单纯地以“数”化“形”或以“形”变“数”无法实现问题的解决,需用综合两种方法,根据题目要求进行“数”与“形”互化,以找到解题的突破口,实现问题的顺利求解. 例6 (2018年全国卷理数第16题)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是________. 分析:从“数”的层面理解函数f(x),可知f(x)为R上的周期函数,最小正周期为2π,同时f(x)为R上的奇函数.从“形”的层面理解f(x),由周期性,故本题只需求f(x)在一周期内的最小值,由奇偶性,问题转化为求解f(x)在区间[-π,π]内的最小值,根据图像的对称性,问题转化为研究f(x)在区间[0,π]内的最值情况. 例7 (2020新高考全国卷 I第21题(2)小题)已知函数f(x)=aex-1-lnx+lna,若f(x)≥1,求a的取值范围. 分析:处理含参问题,若能够充分利用表达式“数”的结构特点和函数图像“形”的特征,通过“形”“数”互变、互补来进行求解,则往往能收到意想不到的效果. 个人数学学习的优劣和数学才能的大小往往不在于数学知识的多寡,而在于数学思想方法的素养[2].随着学生毕业走向社会,学校所学知识会慢慢忘记,方法会渐渐生疏,唯有哪些数学的精神、数学的思维方法能够长久植根于学生的内心,伴随他们成长,让他们受益一生.教师在日常教学中,要充分发掘教学资源中所蕴含的数学思想,有意识的在教学中进行渗透,让学生在潜移默化中去领悟、积淀、凝结并内化为他们的思维品质,达到促进学生能力与素养提升的目的.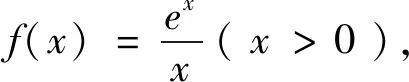
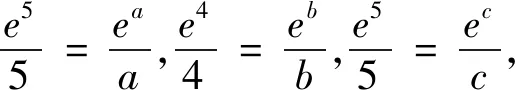
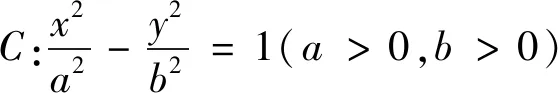
2、以“形”变“数”,将复杂问题简单化
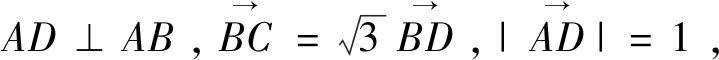

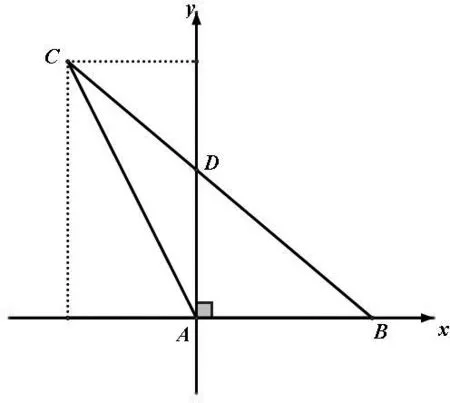
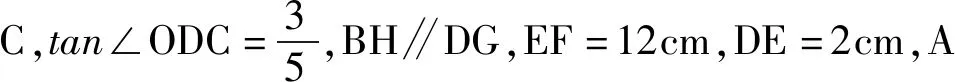
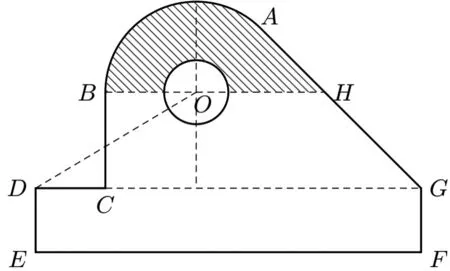

3、“形”“数”互变,强化代数与几何的联系