对线性交叉递推数列问题的探究

江苏省海安高级中学 (226600) 吉海波

一、考题呈现

(2020年4月赤峰市高三模考理18)已知数列{an}和{bn}满足：a1=2，b1=-1，an=2an-1-bn-1，bn=2bn-1-an-1,n∈N*，n≥2.

(1)求证：数列{an-bn}为等比数列；

该考题结构对称、优美，两个线性递推关系式关系紧密，其中证明数列为等比数列{an-bn}是解题的基础，求数列{an}的通项公式是解题的关键.

二、求解策略探析

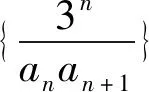
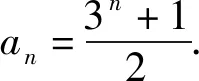
点评：由于题中给出的两个线性递推式中都没有常数项，因而这里运用的“加减运算”是最基本也是最简洁的策略.该策略依据两个线性递推式的特点，并结合(1)的目标，利用两式相加和相减运算，先从整体上证明数列是等比或等差数列，然后再求得个体数列的通项公式的.

分析2：(1)要证数列{an-bn}为等比数列，由于目标明确，可运用“待定系数”策略，只要证存在非零常数q，使得an-bn=q(an-1-bn-1)即可.

策略2 (待定系数) (1)设an-bn=q(an-1-bn-1)(q≠0)，则(2an-1-bn-1)-(2bn-1-an-1)=q(an-1-bn-1)，整理得3(an-1-bn-1)=q(an-1-bn-1).所以q=3，所以an-bn=3(an-1-bn-1).又a1-b1=3，所以数列{an-bn}是以3为首项，3为公比的等比数列.

(2)同策略1.

点评：该策略依据(1)的目标，先从整体上考虑利用待定系数列出关系式，然后求出待定系数后求解的.对于所证的目标明确的这类问题，“待定系数”是一种可行有效的策略.

分析3：从代数方程的角度两个线性递推式可看成二元一次方程组，通过消元降维分别得到单个数列的递推关系，再进行求解.

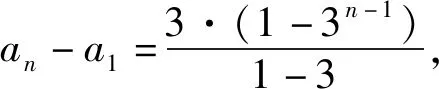
(2)同解法1.

点评：该策略以数列{an}为主,在求解的过程中还运用到了“累加法”求和，同学们需好好体会.就该题而言，应用该策略实在是有点“小题大做”，纯粹是为了说明“消元降维”是求解这类线性递推数列问题一般性的策略.

三、拓展变式

上述的模考题中，线性递推关系中的系数交替，而且没有常数项，在“线性交叉递推数列”一类问题中是最为基础、简洁的一种类型.在此基础上，下面逐步拓展、变式为更为一般的情形.

拓展1 系数交叉，常数项不为0，目标明确

变式1 (2019年高考全国Ⅱ卷理科第19题)已知数列{an}和{bn}满足a1=1，b1=0，4an+1=3an-bn+4，4bn+1=3bn-an-4.

(1)证明： {an+bn}是等比数列，{an-bn}是等差数列；

(2)求{an}和{bn}的通项公式.

分析：考题中的三种策略完全适用于这类问题，按其中一种方法求解即可.

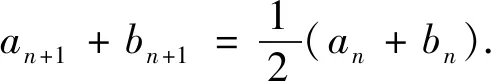
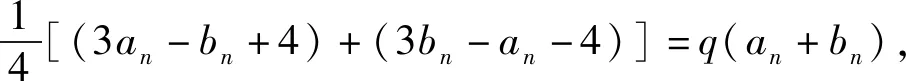
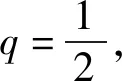
(2)同解法1.

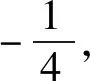
拓展2 系数交替，目标不明确

变式2 已知数列{an}和{bn}满足a1=2，b1=1，4an+1=3an+bn+4，4bn+1=3bn+an+4.求{an}和{bn}的通项公式.

拓展3 系数无关

变式3 已知数列{an}和{bn}满足a1=1，b1=5，an+1=-2an+bn+2，bn+1=3bn-4an+4，求{an}和{bn}的通项公式.

分析：由于两个递推式中的系数没有关系，可从代数方程的角度，利用消元降维的策略求解.

解：(消元降维)由an+1=-2an+bn+2，得bn=an+1+2an-2，所以bn+2+2an+1-2.代入bn+1=3bn-4an+4，得an+2+2an+1-2=3(an+1+2an-2)-4an+4，整理得an+2-an+1-2an=0，即an+2+an+1=2(an+1+an)，所以数列{an+1+an}是首项为a2+a1=6，公比为2的等比数列，故得an+1+an=6·2n-1=3·2n.所以an+1-2n+1=-(an-2n)，即数列{an-2n}是首项为-1，公比为-1的等比数列，所以an-2n=(-1)n，从而得an=2n+(-1)n.所以bn=an+1+2an-2=2n+2+(-1)n-2.可求得an=2n+(-1)n，bn=2n+2+(-1)n-2.

四、题型归纳

通过上述考题和变式题，对“线性交叉递推数列”问题的题型和求解策略归纳如下：