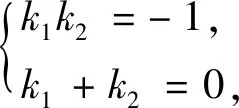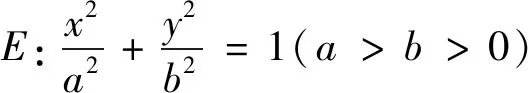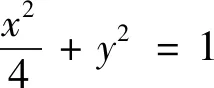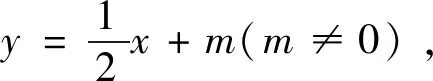赏析高考试题,感悟解几本质*
2022-01-22江苏省扬州市新华中学225009王梅蓉
江苏省扬州市新华中学 (225009) 王梅蓉
江苏省扬州中学 (225009) 戚有建
很多高考题看起来很平凡,实际上却平而不凡、丰富多彩,都是专家经过精心思考编制出来的,是专家智慧的集中体现,所以有很大的研究价值,本文从2021年新高考Ⅰ卷的一道解几题出发,首先研究问题的各种解法,然后对问题进行了推广研究、类比,最后给出结论的相关应用.
一.考题展示
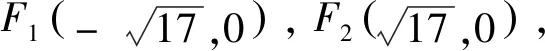
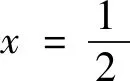

点评:本题是2021年新高考Ⅰ卷的21题,是压轴题、选拔题.第(1)问学生很容易上手,先确定曲线的类型,再确定基本量.第(2)问实际上是个定值问题,意在考查用方程来研究曲线的性质,即用代数方法(坐标法)来研究几何问题(定值问题).本题看起来很平凡,实际上却有一定难度和区分度,有很大的研究价值,我们重点研究第(2)问.
二.解法研究
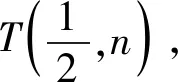
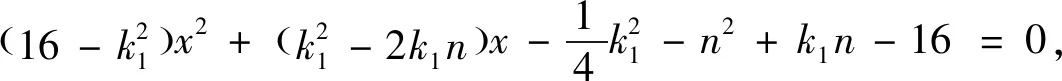
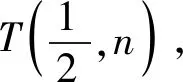
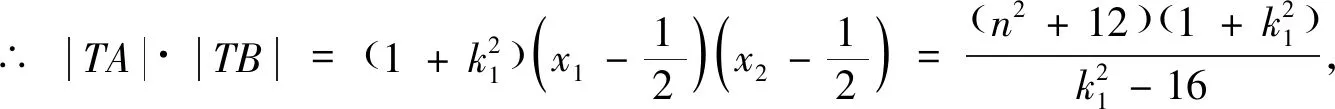
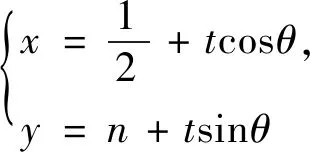
即cos2θ=cos2β,∵θ≠β,∴cosθ=-cosβ,∵k1≠k2,∴k1+k2=0.
点评:解法2是借助直线的参数方程来处理,其中参数t的几何意义是关键,但2017版新课标对直线的参数方程不做要求,所以学生不容易想到这个方法.
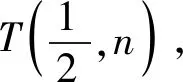
点评:解法3是构建二次曲线系来处理问题,运算量大大简化.因为该二次曲线系(即①式)表示圆,所以等式的左边应该不含xy,所以k1+k2=0.解法3是站在方程的高度来处理几何问题,充分体现了解析几何的基本思想.
三.研究推广
题目中|TA|·|TB|=|TP|·|TQ|实际上相当于A,B,P,Q四点共圆,将本题推广为一般双曲线可得如下结论:
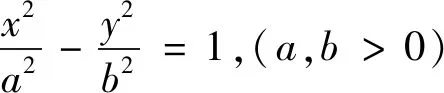
将结论1中的“双曲线”改为“椭圆、抛物线”,结论成立吗?研究后发现仍然成立,即有下面结论:
结论2 已知两条直线y=k1x+b1,y=k2x+b2与圆锥曲线ax2+by2+cx+dy+e=0(a≠b)交于四个点A,B,P,Q,则A,B,P,Q四点共圆的充要条件是k1+k2=0.
结论1、结论2的证明过程与上面类似,从略.
四.结论应用
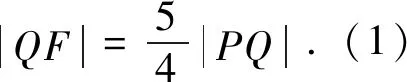
解析: (1)y2=4x(过程从略).