我国股指期货与现货市场风险溢出效应研究

淳伟德 朱航聪

【关键词】 股指期货; 风险溢出; 混频时变Copula; CoVaR

【中图分类号】 F832.5  【文献标识码】 A  【文章编号】 1004-5937（2022）03-0009-07

一、引言

国际金融危机给金融市场带来剧烈动荡和危害，而股票市场作为金融市场的核心将首当其冲。股价的暴跌和异常波动，在阻碍经济健康良好运行的同时还对其造成了一定程度的破坏。我国经济发展方式和结构在不断优化的同时不可避免地带来经济不确定因素，从而对金融市场的运行产生影响。与此同时，宏观经济运行状况会通过边际效用、资本成本和贴现率等因素对金融市场产生影响[ 1 ]，因此，在分析金融市场运行状况时应综合宏观经济运行背景加以考虑。随着金融的不断发展，金融市场间的联动性也在不断加强，这使得一个市场产生的风险极易通过金融市场间的关联结构发生溢出，从而带来风险隐患，甚至造成系统性金融风险的积累，这给“牢牢守住不发生系统性金融风险的底线”工作形成了压力。习近平总书记在2019年中共中央政治局第十三次集体学习时强调，要“坚决打好防范化解包括金融风险在内的重大风险攻坚战”。然而，风险溢出效应显著增加了金融风险的危害波及性，导致风险的防范变得困难，给监管层的风控工作带来了严峻挑战。在此背景下，应对这一挑战的有效方法是充分运用高频微观和低频宏观数据的有效信息，准确测度金融市场间的相依结构和风险溢出，从而为监控化解金融风险和推动金融改革开放有序进行提供一定的参考依据和实证支撑。

股指期货是一种以股票指数为标的物的期货，根据合约确定交割数量和日期，并以现金结算差价，具备价格发现、套期保值等作用。2010年4月16日，我国第一个金融期货——沪深300股指期货在中国金融期货交易所正式上市，标志着我国金融市场得到进一步发展和拓宽，也引起了投资者的广泛关注。部分投资者期望股指期货的推出能够逆转我国股票市场剧烈波动的常态，也有不少投资者担忧在股指期货推出后，其中的过度投机行为会给股票市场增加风险。尤其是2015年6月后，人们开始进一步担忧股指期货是否加剧了股指现货的暴跌，从而加剧了金融风险。此外，股指期货作为一种新兴金融资产，对其进行风险溢出效应的研究将为后续金融市场的进一步开放提供一定的参考价值。

学术界目前对股指期货市场和现货市场的研究主要集中于价格发现、波动溢出及跳跃风险三个方面。陶利斌等[ 2 ]研究发现股指期货的价格发现能力较现货市场更强。赵慧敏等[ 3 ]使用BVGJR-GARCH-BEEK模型分析了不同市场行情下股指期现货市场的价格发现作用、波动溢出关系和跳跃风险。宫晓莉等[ 4 ]通过构建双层跳跃扩散模型研究发现，股指期货波动性相较于股指现货强但持久性低，同时两个市场间存在双向跳跃风险溢出。陈海强和张传海[ 5 ]通过分解跳跃类型分析了股指期货交易的跳跃风险，发现股指期货交易增加了股市的大跳风险而减小了其小跳风险。通过对已有文献的梳理，笔者发现现有研究较少对两个市场间的双向极端风险溢出关系进行研究，因此，本文将致力于对股指期现货间的极端风险溢出效应进行研究。

迄今，已有大量学者对金融市场间的风险关系进行了研究，并取得了较为丰硕的研究成果。从研究方法来看，主要有Granger因果检验法[ 6 ]、GARCH族模型[ 7-8 ]、协整检验[ 9 ]等，风险测度的指标主要有VaR、CoVaR。然而，金融市场收益率不一定服从相同分布，GARCH族模型需假设服从相同分布，具有一定局限性;Granger因果检验法未能对金融市场间的风险溢出强度进行测度;协整检验对金融市场间长期均衡关系的研究，难以处理短期关系;VaR方法由于不具备次可加性，不能满足一致性风险测度要求，同时也无法反映金融市场间的风险溢出。Adrian和Brunnermeier[ 10 ]提出的CoVaR方法不仅满足了一致性风险测度要求，而且可以度量一个金融市场在另一个金融市场发生风险时的条件在险价值，得出风险溢出的强度和方向，为分析金融市场间的风险溢出效应提供了新的思路。有部分学者[ 11-13 ]基于分位数回归计算CoVaR，但此方法无法刻画金融市场普遍存在的非线性关系，具有一定局限性。而基于Copula方法计算的CoVaR能够有力捕捉金融市场间的非线性相依结构，从而更好地测度极端风险溢出。已有学者[ 14-16 ]运用此方法研究金融市场间的风险溢出效应，并取得了较好的结果。

令人遗憾的是，目前关于风险溢出效应的研究主要是基于高频日度收益率数据而展开的，没有将低频宏观经济背景纳入考量。金融市场间的波动关系和相依结構不仅会受到高频金融市场数据影响，而且会受到低频宏观经济数据影响。经济兴，金融兴，经济和金融是密不可分的关系，将宏观经济运行中的有效信息加以运用，有助于更加充分地分析金融市场的波动关系和相依结构并提高边缘分布拟合效果，从而更好地描述其间的风险溢出效应。

为了解决数据频率不匹配的问题，目前学术界采用的方法有插值法、加总替代法等，此类方法是将低频数据或高频数据进行相互转换。值得注意的是上述对数据进行变频的方法会使数据中的有效信息丢失，并产生模型设定错误和结论偏差[ 17-18 ]。Engle等[ 19 ]在Ghysels等[ 17 ]提出的混频抽样（MIDAS）的基础上建立了混频自回归条件异方差模型（GARCH-MIDAS），该模型能够纳入低频宏观经济变量，将金融市场收益率序列中的波动成分分解为长期成分和短期成分，实现混频数据视角下的分析，从而提高边缘分布拟合效果。

有鉴于此，本文构建了GARCH-MIDAS-Copula-CoVaR模型。首先，通过混频模型对比分析股指期货和现货的波动率，以期考察宏观变量对金融市场的作用，同时提高边缘分布的拟合效果;其次，将得到的残差经过概率积分转换后运用时变Copula函数分析动态相依关系;最后，通过CoVaR方法分析股指期货与现货市场间的风险溢出效应，为进一步探究两个市场在极端风险事件下的关系、保障金融平稳安全运行提供了参考依据。

二、模型设定

（一）构建边缘分布模型

本文使用的GARCH-MIDAS模型对收益率序列设定如下：

其中，将收益率序列的波动性分解为低频长期成分？子t和高频短期成分gi，t，并设定短期成分gi，t服从GJR-GARCH（1，1）过程，长期成分？子t为受已实现波动率RVt和宏观经济变量Xt影响的MIDAS滤波方程。

（二）时变Copula模型

本文使用的时变Gaussian Copula和时变t Copula的相关系数？籽基于DCC（1，1）过程进行演化，形成DCC-Gaussian-Copula和DCC-t-Copula模型。演化方程如下：

其中，Q为标准化残差序列的协方差矩阵，Q*t为对角元素是Qt平方根、非对角元素是0的方阵。

（三）CoVaR方法

CoVaR可以用来衡量风险溢出效应，在1-q的置信水平下，当某一金融市场i某时刻处于某风险价值水平时，另一金融市场j的条件在险价值：

对式（10）求解并计算反函数即可得到风险溢出值。

为了更好地说明金融市场i发生风险事件对j的风险溢出效应，定义溢出条件风险价值为？驻CoVaRj│iq，t，其表达式为：

考虑到风险溢出规模由于量纲问题存在较大差异，因此对溢出条件风险价值进行标准化处理：

另外，无条件风险价值由式（13）计算得出，t-1为边缘分布函数反函数的q分位数：

（四）Backtesting检验

为确保本文使用的模型能够准确测度出股指期货与现货的双向风险溢出效应，根据Kupiec[ 20 ]提出的Backtesting方法进行后验检验，构造“碰撞序列”：

Ht=1，if Rt≤VaRt0，if Rt>VaRt  （14）

假定显著性水平为p，T为碰撞序列总长度，N为Rt≤VaRt的数量，当E[Ht]=p成立，则式（15）应该服从自由度为1的？字2分布：

进一步根据Christoffersen[ 21 ]提出的独立性检验，在原假设成立的条件下，式（16）应服从自由度为2的？字2分布：

当Rt≤VaRt时，构建新的碰撞序列如式（17），并遵循上述碰撞序列检验方式进行Backtesting检验。

在显著性水平p上，如果计算出的统计量值大于？字分布的临界值，应当拒绝原假设，若无法拒绝原假设，则表明本文使用的模型是合适的。为了更直观地判断，使用检验统计量的P值进行判定：P值越大，表明模型越具有准确性和独立性，即使用此模型进行风险测度是合理且有效的。

三、实证分析

（一）数据选取与描述性统计

沪深300股指期货是我国最早成立的金融期货，同时，作为股指期货标的物的沪深300指数涵盖了我国A股约60%的市值，具有良好的市场代表性。本文选取沪深300股指期货作为股指期货的代表，因当月合约的成交量最大且流动性最强，选取当月连续合约为研究对象。选取沪深300指数作为股指现货的代表。宏观变量选取中国社会消费品零售总额、固定资产投资完成额和银行间同业拆借加权利率作为消费（Sale）、投资（Invest）和利率（Rate）的代理变量，其中除利率外，其他变量均采用X12方法季节调整后进行对数差分处理。

综合考虑沪深300股指期货成立时间和宏观月度变量的可得性，选取样本区间为2010年5月4日至2020年12月31日，股指期现货日度数据共计2 595组，采用收益价格的自然对数差分形式：rt=100×ln（pt/pt-1），其中pt为第t日的收盘价。宏观变量均为月度数据，对应样本区间为2010年5月至2020年12月，共计128组。

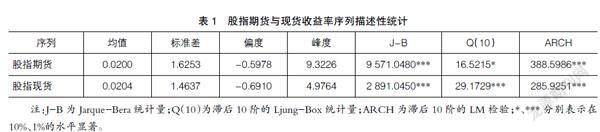
表1的描述性统计显示，股指期货的波动性大于股指现货，同时两个收益率序列都呈现出“尖峰厚尾”特征，J-B统计量均显著拒绝了两个收益率序列服从正态分布的假设。Q（10）统计量和ARCH统计量表明，两个收益率序列存在自相关和异方差性。

（二）混频时变Copula

1.边缘分布参数估计

在双因子GARCH-MIDAS模型参数估计过程中，采用准极大似然估计法（QML）。为了保证滞后变量的权重呈衰减形式，即滞后期越短对当期影响最大，权重函数中？棕1设置为1。

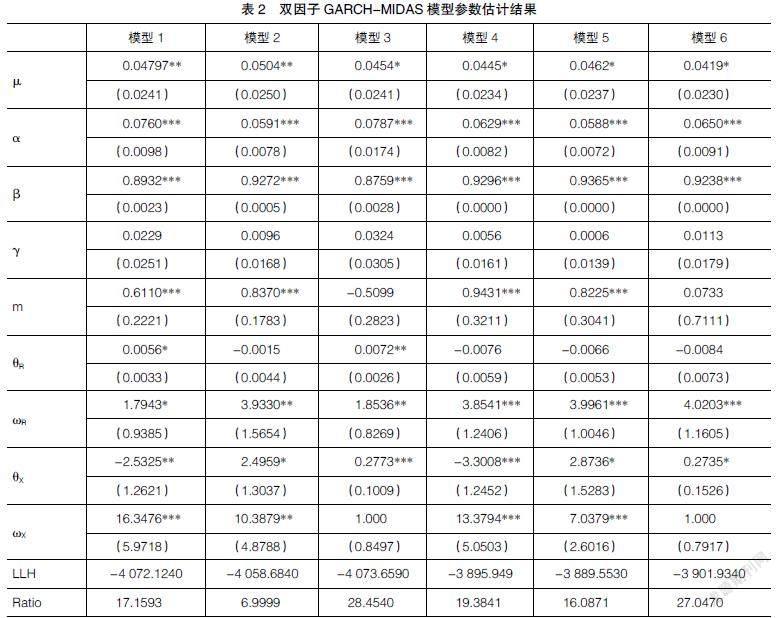
从表2可以看到，所有模型測度GARCH效应的参数？滋，？琢，？茁均在统计意义上显著，并且？琢+？茁<1且接近1，表明在纳入宏观经济变量后，股指期货与现货的短期波动仍呈现出明显的波动聚集效应;测度月度已实现波动率的参数？兹R在模型1和3中显著，表明其增加了股指期货的长期波动。

对于宏观经济变量，对比分析股指期货与现货的参数？兹X，？棕X，本文发现：

消费和投资对股指期货与现货的影响方向一致，其中消费的增长会减少两个市场的长期波动，而投资的增长会增加两个市场的长期波动。出现此种情形的原因，本文认为可能是投资者在消费上的增加会使其在金融市场投入的资金量变少，进而减少交易活动，导致市场长期波动减小，而投资的增加很大一部分来源于我国上市企业的投入再生产，通过生产流通等环节带来的收益最终会影响到股票价格，导致市场长期波动增加。

利率的增加会增加股指期货与现货的长期波动。本文认为，利率的增加会提升企业的融资成本并影响投资者的资产配置，导致金融市场出现波动，比如利率的增加会提升以债券代表的金融资产的吸引力，使股指期货和现货市场的成交量下降，从而出现波动现象。同时，本文注意到利率的调整对股市波动的影响有限，一方面由于我国一直采取稳健的货币政策对利率进行合理微调，另一方面我国的货币政策传导机制仍处于不断完善和发展进程中，存在传导不通畅的状况。

从Ratio结果来看，RV+Rate模型中的长期趋势占总波动成分比例最高，其次为RV+Sale模型，占比最低的为RV+Invest模型。但长期趋势占比最高的模型也没有超过30%，这表明短期波动仍然是股指期货与现货市场的主要风险来源，需要加以监控和防范。

2.时变Copula

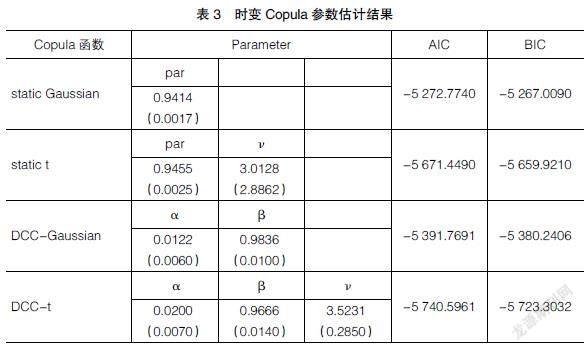
选用长期趋势占比最高的GARCH-MIDAS-RV+Rate模型，将获得的残差进行概率积分转换，并通过K-S检验验证了其满足使用Copula函数的条件。参数估计结果如表3。同时使用静态Copula函数进行计算对比，发现时变Copula函数具有更好的拟合效果，且时变DCC-t- Copula具有最好的拟合效果。

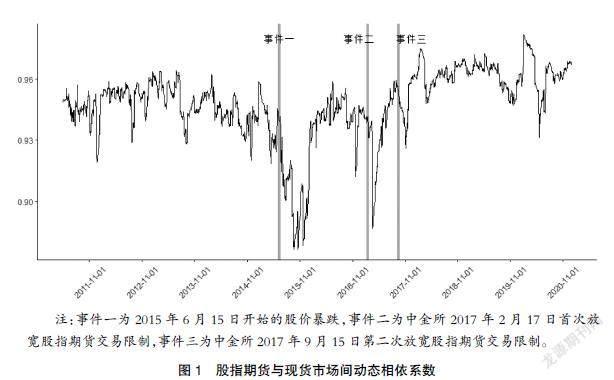
圖1展示了股指期货与现货市场的动态相依系数，可以发现在2015年6月前，两个市场的相依性在一个区间稳定变化。但在2015年6月后，两个市场的相依性呈现下降态势，表明在此期间，两个市场的关联程度在不断下降。究其原因，本文认为一方面是期货的风险对冲在初期发挥作用;另一方面是中金所在2015年9月推出了最严限令，采取提高非套期保值持仓交易保证金到40%、平仓手续费提高到万分之二十三等多重措施限制交易，遏制了股指期货的流动性，使得两个市场的相依性减弱。2015年6月后，中国金融市场交易规则和制度不断完善，投资者的投资理念也在不断提升，股指期货与现货市场的相依性缓慢上升。值得注意的是，2017年2月，两个市场的相依性在短期内出现了较为剧烈的下降，而这正是中金所在最严限令后首次对股指期货交易松绑的时间;此外，在2017年9月15日第二次对股指期货交易松绑后，两个市场的相依性在短期内又出现了较为剧烈的下降。究其原因，本文认为这是投资者对中金所调整交易规则存在不确定预期，从避险和观望的角度暂停和减少了交易行为，导致两个市场的相依性暂时下降。

3.风险溢出效应分析

从VaR的数值可以看出，股指期货的无条件风险要大于股指现货，这是因为股指期货市场本身存在更高杠杆的同时也具备了较高的波动性。通过对比CoVaR和VaR数值，可以发现，如果没有考虑条件在险价值，风险会被严重低估。此外，通过对比不同显著性水平下的风险价值，发现当显著性水平下降时，条件在险价值提高，换言之，表明其中一个市场自身风险加剧时，会加大对另一个市场的风险外溢，从而造成更强的冲击。

从%CoVaR来看，以5%的显著性水平为例，股指现货对期货市场的风险溢出效应为115.7523%，而股指期货对现货市场的风险溢出效应为94.3269%，这表明两个市场间存在非对称的风险溢出关系，且现货市场对期货市场的风险冲击更为剧烈，这与刘庆富和华仁海[ 22 ]的研究结论一致。

无条件风险价值VaR和条件风险价值CoVaR的Backtesting结果如表5所示。可以看到，所有统计量的P值都大于0.05，即在5%的显著性水平都通过了检验，这表明本文模型的计算是准确和有效的。因此，使用本文构建的模型能够对极端风险情况下的风险溢出进行准确测量。

四、结论与启示

本文扩展了已有研究视角，运用混频分析技术综合提取了高频微观数据和低频宏观数据的有效信息，提高了边缘分布拟合效果，在运用时变DCC-t-Copula模型刻画股指期货与现货市场动态相依关系的基础上，结合CoVaR模型进一步分析了股指期货与现货市场间的极端风险溢出效应，并通过Backtesting结果证明了本文模型测度风险溢出效应的准确性和有效性。研究结果表明：（1）宏观经济变量会对金融市场长期波动产生显著影响，从而进一步影响金融市场间的相依关系和风险溢出效应。这表明使用低频宏观数据中的有效信息将有助于更加准确地测度金融风险。其中，消费会减小股指期货与现货市场的波动，而投资和利率会增加股指期货与现货市场的波动。与此同时，宏观经济运行状况还可以作为参考金融市场运行状况的一个风向标。（2）股指期货与现货市场间存在比较高的动态相依性，并会受到政策规则变化的影响。（3）使用无条件风险价值对风险进行测度时会忽略金融市场间的风险溢出关系，而使用条件在险价值不仅可以测度出风险溢出的强度，还可以获取风险溢出的方向。实证结果表明，股指期货与现货市场间存在非对称的双向极端风险溢出效应，其中股指现货市场对期货市场的风险溢出强度要大于股指期货市场对现货市场的风险溢出强度。此外，鉴于股指现货风险溢出的高强度性，监管层对股指现货市场的稳定运行应给予更为密切的关注。（4）随着显著性水平的减少，风险溢出效应的强度会加大。这表明一个市场若自身风险加剧，会使另一个市场的风险溢出加剧，从而造成更加严重的后果。因此，对极端风险采取严密的监测和防范措施十分必要。

由此得到的启示有：（1）监管层进行风险管理时，要进一步立足宏观经济背景，掌握消费、投资、利率等经济变量的状况，并针对性地进行风险调控。（2）股指期货与现货市场间存在密切的相依性，监管层应该从整体的视角出发，综合考量两个市场的运行情况，若仅单独对某一市场进行监控和调控，可能会造成对风险的低估并导致调控措施的无效化。（3）股指现货市场作为我国金融市场的重要组成部分，对股指期货市场的风险溢出程度更为剧烈，但也不可忽视期货市场对现货的风险溢出。因此，监管层要尽力确保金融市场的稳定，避免其中一个市场产生的风险外溢对另一个市场造成严重的冲击，这有助于营造稳定的市场环境，从而进一步促进金融市场健康、有序、平稳地发展。

【参考文献】

[1] 刘凤根，吴军传，杨希特，等.基于混频数据模型的宏观经济对股票市场波动的长期动态影响研究[J].中国管理科学，2020，28（10）：65-76.

[2] 陶利斌，潘婉彬，黄筠哲.沪深300股指期货价格发现能力的变化及其决定因素[J].金融研究，2014（4）：128-142.

[3] 赵慧敏，陈晓倩，黄嵩.中国股指期货和现货市场信息传导关系在牛熊市中的异化现象[J].系统工程理论与实践，2018，38（4）：863-872.

[4] 宫晓莉，熊熊，庄新田.广义双指数分布的跳跃扩散模型下股指期货波动研究[J].管理科学，2018，31（3）：149-159.

[5] 陈海强，张传海.股指期货交易会降低股市跳跃风险吗？[J].经济研究，2015，50（1）：153-167.

[6] 侯县平，黄登仕，徐凯，等.金融危机对中国证券市场传染效应的影响[J].系统工程学报，2015，30（3）：331-343.

[7] 刘璐，韩浩.我国保险市场与银行市场间的风险溢出效应研究：基于上市银行和保险公司的实证分析[J].保险研究，2016（12）：3-14.

[8] 寇明婷，杨海珍，肖明.中国股票市场与货币政策的互动关系：基于股指期货推出前后的比较研究[J].管理评论，2016，28（4）：21-29.

[9] 刘堂发.我国股指期货与现货市场关系分析[J].会计之友，2016（11）：41-43.

[10] ADRIAN T，BRUNNERMEIER M K.CoVaR[J].The American Economic Review，2016，106（7）：1705-1741.

[11] 陈建青，王擎，许韶辉.金融行业间的系统性金融风险溢出效应研究[J].数量经济技术经济研究，2015，32（9）：89-100.

[12] 曾裕峰，温湖炜，陈学彬.股市互联、尾部风险传染与系统重要性市场：基于多元分位数回归模型的分析[J].国际金融研究，2017（9）：86-96.

[13] 刘超，刘彬彬.金融机构尾部风险溢出效应：基于改进非对称CoVaR模型的研究[J].统计研究，2020，37（12）：58-74.

[14] 沈悦，戴士伟，陈锟.房价过度波动的系统性风险溢出效应测度：基于GARCH-Copula-CoVaR模型[J].中央财经大学学报，2016（3）：88-95.

[15] 侯縣平，傅春燕，林子枭，等.极端风险溢出效应的定量测度及非对称性：来自中国股市与债市的经验证据[J].管理评论，2020，32（9）：55-67.

[16] 赵如波，田益祥，田伟.基于GAS t-Copula模型的金融市场非对称风险溢出效应测度研究[J].运筹与管理，2021，30（2）：176-183.

[17] GHYSELS E，SINKO A，VALKANOV R.MIDAS regressions：further results and new directions[J]. Econometric Reviews，2007，26（1）：53-90.

[18] FERRARA L，GURRIN P.What are the macroeconomic effects of high-frequency uncertainty shocks？[J].Journal of Applied Econometrics，2018，33（5）：662-679.

[19] ENGLE R F，GHYSELS E，SOHN B.Stock market volatility and macroeconomic fundamentals[J].Review of Economics and Statistics，2013，95（3）：776-797.

[20] KUPIEC P H.Techniques for verifying the accuracy of risk measurement models[J].The Journal of Derivatives，1995，3（2）：73-84.

[21] CHRISTOFFERSEN P F.Evaluating interval forecasts[J].International Economic Review，1998，39（4）：841-862.

[22] 刘庆富，华仁海.中国股指期货与股票现货市场之间的风险传递效应研究[J].统计研究，2011，28（11）：84-90.