基于快速多极子边界元法的齿轮箱声场分析
2022-01-21刘学良冯治恒吴海军
刘学良,冯治恒,吴海军,莫 蓉
(1.上海交通大学机械系统与振动国家重点实验室,上海 200240;2.广西柳工机械股份有限公司,广西柳州 545007)
0 引 言
齿轮箱在工程机械中非常重要,主要用于发动机动力输入、扭矩输出至轴系等方面。现今齿轮箱的辐射噪声越来越受到重视[1-2],其不仅会产生环境的噪声污染问题,还会影响减速器的正常工作,降低设备的疲劳寿命。因此,准确地计算齿轮箱的辐射噪声,对其进行噪声评估以及低噪声优化有着重要的意义。随着传动技术的提升,如何在高转速、大功率、大扭矩的齿轮箱中降低振动和辐射噪声,是工程设计中的严峻课题[3],同时也对噪声预测提出了更高的要求。
齿轮箱的噪声预测方法有统计能量分析(Statistical Energy Analysis,SEA)、有限元法(Finite Element Method,FEM)、边界元法(Boundary Element Method,BEM)[4]等多种方法,其中BEM是一种基于积分方程的计算方法[5]。边界元方法仅需对模型边界进行离散,并且求解精度较高,能自动满足无限远处的 Sommerfeld辐射条件,因而非常适用于分析自由空间下的声传播问题[6]。因此本文选用边界元方法对齿轮箱进行声场分析。目前国内外关于边界元法在齿轮箱声场的噪声预测有一定的研究。王胜男等[7]运用边界元法分析了二级齿轮箱的辐射噪声;焦映厚等[8]建立了大型立式齿轮箱的外声场边界元模型并分析了辐射声场;Le Moyne等[9]用边界元法分析了齿轮箱的加筋板对声辐射的影响。但以上研究所采用的均为传统边界元方法(Conventional Boundary Element Method,CBEM)。CBEM存在着求解效率低、内存占用大的固有缺陷[10],无法用于大规模声学问题的计算。而齿轮箱在不同工况下的噪声频谱一般比较宽,在宽频段内的扫频分析更加耗时,不利于产品声学设计的及时评估及优化设计。因此需要考虑加速算法。而快速多极子的方法出现,将边界元方法的计算量和存储量降低到O(N)量级,其中N为计算模型的自由度,从而使边界元方法在求解大规模声学问题上得到了迅速发展[11]。
本文发展了宽频快速多极子边界元算法,并运用了多核并行方法加速计算,克服了以往传统边界元方法求解效率低、内存占用大的缺点。通过对工程中的某齿轮箱进行建模以及有限元仿真,得到模型表面节点的振速信息。再运用所发展的快速多极子边界元方法对齿轮箱进行辐射声场分析以及扫频计算,大幅度地降低了求解时间,为后续的低噪声优化设计提供了理论依据。
1 边界元法理论
在均匀理想介质中,线性声学波动方程[12]为




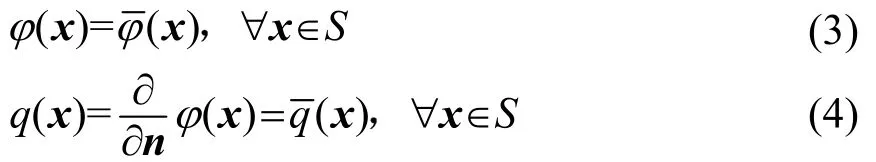

可以得到传统边界积分方程(Conventional Boundary Integral Equation,CBIE)为


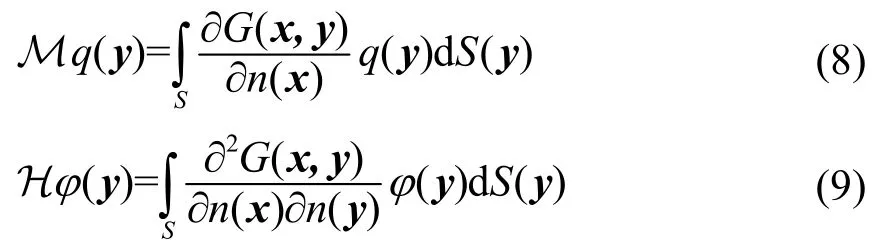
可以得到相应的超奇异边界积分方程(Hypersingular Boundary Integral Equation,HBIE)为

2 数值算法实现
2.1 边界元法数值实现
如前所述,将式(7)、(10)进行线性组合,得到的Burton-Miller方程为


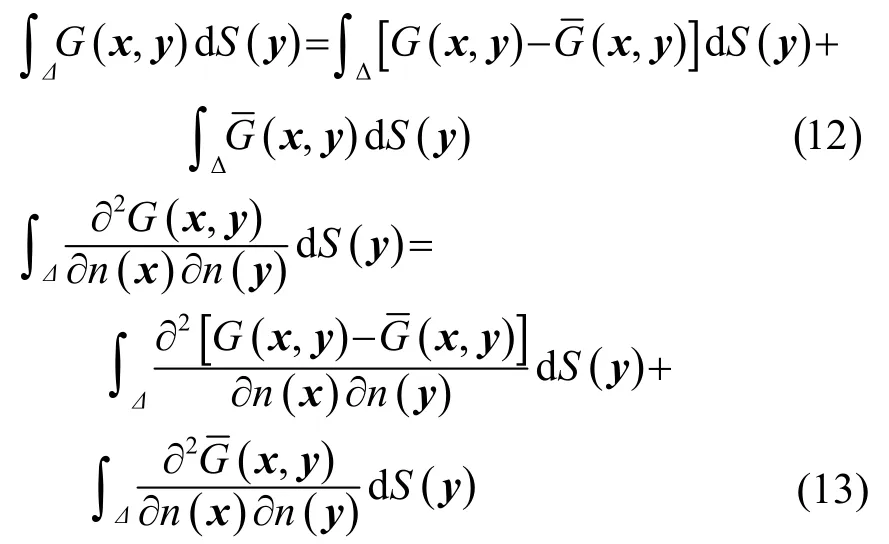
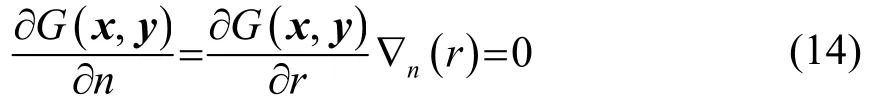
采用三角形或者四边形常数单元进行离散,并代入已知边界条件,将未知边界量及其系数重组,最终可以生成方程:


2.2 快速多极子方法
快速多极子方法[18-20]在20世纪80年代提出。该方法的引入,极大地降低了边界元法的求解时间和内存占用量,推动了边界元法的快速发展。快速多极子方法的核心思想是Green函数在高频下的平面波展开和低频下的级数展开。通过将源点对场点的贡献进行分块层级传递,达到降低计算量的目的。以高频为例,其平面波展开形式为:


其中:x为场点;y为源点;k为波数;xc是本地系数展开中心;yc是源点矩的汇聚中心;为球面上的法向量;为向量的模,快速算法的具体步骤如图1所示。
首先,通过模型离散和算法实现,生成树状结构。其次,通过上行、下行计算两个步骤计算b向量,上行计算主要为各个栅格的源点矩计算,其公式为

其中,M为源点矩,yc为树结构中栅格的中心点。下行运算主要为源点矩转移(M2M)、源点矩到本地展开系数传递(M2L)及本地展开系数转移(L2L)。通过层级传递,最终计算得到源点对场点的贡献。本文通过运用快速多极子算法,最终完成了低频、高频的快速多极子边界元方法,并将两者结合,最终发展了宽频的快速多极子边界元方法。

图1 快速多极子算法流程图Fig.1 The flowchart of fast multipole method
3 齿轮箱模型处理
3.1 齿轮箱模型
首先建立齿轮箱的几何模型,建模过程中需要对模型进行合理简化,略去较小的倒角和其他细小特征。通过建立齿轮-轴-轴承系统的耦合动力学模型,对齿轮箱进行动力学分析,得到齿轮箱的载荷,并运用有限元法计算齿轮箱的各阶模态。其次,对齿轮箱进行频段为4~2 000 Hz、步长4 Hz的谐响应分析,计算得到各频率下齿轮箱表面的节点振速信息,作为边界元法的输入边界条件。
边界元模型是结构有限元模型的外轮廓,运用商用软件对有限元模型进行网格处理,提取得到齿轮箱轮廓的网格模型如图2所示,其模型参数见表1所示。
3.2 边界条件处理
边界元方法只需要模型表面轮廓的边界条件。将有限元分析所得到的各频率下的齿轮箱表面的节点振速进行分析处理,可以得到离散面单元的声压法向导数,并将其作为边界条件。其中节点声压的法向导数与振速V的关系为
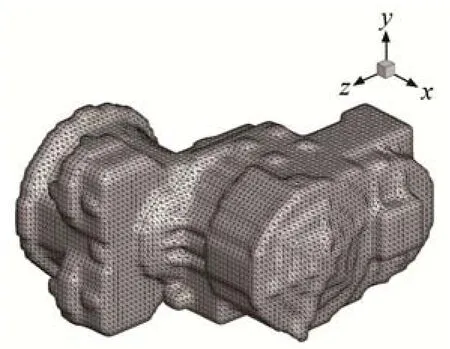
图2 三角形单元划分的模型Fig.2 The model divided with constant triangular elements

表1 齿轮箱模型参数Table 1 The parameters of gear box model

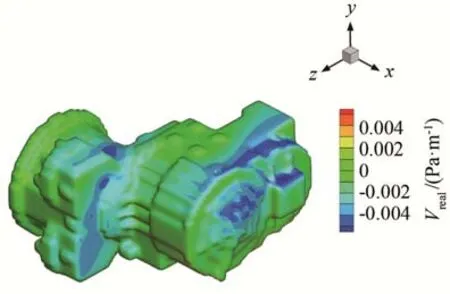
图3 边界条件实部云图Fig.3 Nephogram of the real part of boundary condition
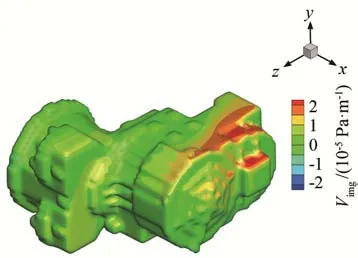
图4 边界条件虚部云图Fig.4 Nephogram of the imaginary part of boundary condition
4 齿轮箱声场分析
本节介绍齿轮箱的声场分析结果,分别计算了频率为 100 Hz时的场点声压、齿轮箱的辐射声场以及4~2 000 Hz的扫频分析。计算所用的计算机主要参数如表2所示。

表2 计算机配置参数Table 2 The configuration parameters of computer
4.1 场点计算
为了验证预测结果的正确性,如图 5所示位置布置场点,计算频率为 100 Hz时的场点声压以及齿轮箱边界声压。

图5 场点分布Fig.5 The distribution of field points
运用快速多极子边界元方法,可以计算得到全空间下齿轮箱表面的声场,其结果如图6、图7所示。
为了验证加速算法的计算精度和效率,对比了快速多极子边界元法与某商用软件的计算结果。商用软件和快速边界元方法在计算参数上的对比如表3所示。快速算法和商用软件的场点计算结果对比见图8所示。
从图8中可以看出,算法与商用软件的计算结果较为接近。
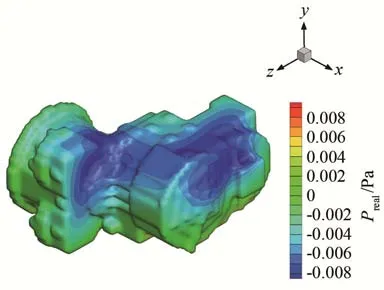
图6 声场实部计算结果Fig.6 Nephogram of the computational results of real part of the sound field
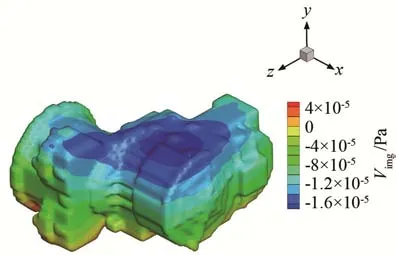
图7 声场虚部计算结果Fig.7 Nephogram of the computational results of imaginary part of the sound field

表3 快速算法和商用软件计算参数对比Table 3 The comparison of parameters between the fast algorithm and the commercial software
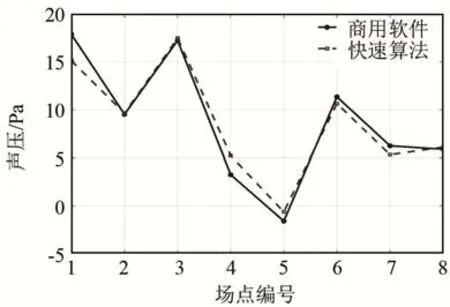
图8 快速算法和商用软件的声场计算结果对比Fig.8 Comparison of sound field computational results between the fast algorithm and the commercial software
4.2 齿轮箱辐射声场计算
该部分通过计算齿轮箱附近的场点,得到频率为 100 Hz时的齿轮箱辐射声场。其场点模型如图9所示。

图9 场点模型Fig.9 The model of field points
圆环模型的圆心坐标为(0,0,0.75)m,内径为1.2 m,外径为 4.8 m,共有 3 202个场点,6 153个单元。运用快速多极子边界元方法进行求解,得到其在100 Hz时的辐射声场如图10、11所示。

图10 齿轮箱辐射声场实部Fig.10 Nephogram of the real part of radiation sound field of the gearbox
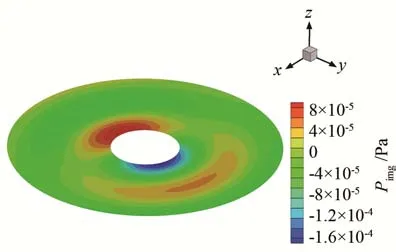
图11 齿轮箱辐射声场虚部Fig.11 Nephogram of the imaginary part of radiation sound field of the gearbox
从云图中可以清楚地看到齿轮箱周围的声场分布,进而为齿轮箱后期的降噪处理和低噪声设计提供理论依据。
4.3 齿轮箱扫频计算
该部分对齿轮箱进行扫频计算,计算频率为4~2 000 Hz,步长为4 Hz,共500步。首先对数据进行处理,得到500步中每一步的边界条件,最终得到包含500步的边界条件文件。将边界条件代入快速算法进行计算,得到扫频计算结果。最终处理数据,得到每一个场点的声压级LSP,其计算公式为

从图12中可以看到,商用软件和快速边界元方法的扫频结果趋势相近,在个别频率处的计算结果有差异。该差异由算法的方法差异所决定,快速边界元方法采用了常数三角形单元进行模型离散,而商用软件采用的是四边形线性单元进行离散。从理论上讲,相同自由度下,线性单元的计算精度略高于常数单元。而在目前齿轮箱的模型中,快速多极子边界元模型的自由度为商用软件所采用模型自由度的2倍,由此分析,理论上快速边界元的计算结果应该更为准确一些。
此外,运用多核并行计算对扫频分析进行加速,最终得到快速多极子边界元方法的计算时间如表4所示。

图12 商用软件和FM-BEM扫频计算得到的4个典型场点的声压谱比较Fig.12 Comparison of the sound pressure spectrums obtained by the frequency sweeping calculations of commercial software and FM-BEM at four typical field points

表4 快速多极子边界元方法计算时间Table 4 The computation time of FM-BEM
从表4中的数据可以看到,运用多核并行计算可以加倍提升计算效率。当采用36核进行计算时,共500步的扫频计算仅需2 h 15 min,大大提高了计算效率。采用多核并行计算的快速多极子边界元方法为齿轮箱噪声预测提供了强大的算力支撑。
5 结 论
本文运用快速多极子边界元方法,通过对齿轮箱辐射声场的系统分析,得到了齿轮箱的声场分布、单频处的场点声压以及扫频声压。通过对比商用软件,验证了该快速多极子边界元方法的准确性。此外,通过运用多核并行计算,进一步加快了计算速度,最终快速完成了齿轮箱的扫频分析,为后续的低噪声优化设计提供了充分的理论依据。
