基于调制FFT的谐振式SAW传感器快速频率估计算法

王威威

1,2，卢孜筱2,3，李红浪2,3，田亚会1,2，柯亚兵2,3

（1.中国科学院声学研究所，北京 100190；2.中国科学院大学，北京 100049；3.国家纳米科学中心，中国科学院纳米科学卓越创新中心，北京 100190）

0 引 言

随着声表面波传感器技术的发展，谐振式SAW传感器由于无线无源、高Q值、抗干扰能力强、灵敏度高等优点，在高动态复杂应用环境中得以广泛使用[1]。例如，在列车轮轴、船舶传动轴、航天发动机等高速环境中[2-4]，要求对应变、扭矩等参量实现快速检测，因此需要研究一种谐振式 SAW传感器快速频率估计算法。

谐振式SAW传感器常使用FFT谱估计的频率估计算法对回波信号进行快速频率估计，但FFT谱估计的频率估计精度受回波信号序列长度的限制[5]，无法满足谐振式SAW传感器的频率估计精度。为了提高FFT谱估计的频率估计精度，人们基于FFT谱估计提出了很多频谱修正方法，其中Rife算法是基于FFT谱估计的经典算法[6]，该算法通过最大谱线与相邻次大谱线估计频率偏移量，对频率估计进行修正，计算量小。但当实际频率在谱线最大值频率附近时，频率估计精度较差且容易受环境影响。文献[7]使用频谱细化与搬移技术对Rife算法的频谱修正方法进行了改进，提出I_Rife算法。该算法很大程度上提高了频率估计精度，但因其需要计算4个实数点的离散傅里叶变换对频谱进行细化，使得计算量增大。文献[8]提出了一种针对实信号进行快速频率估计的调制FFT算法，克服了FFT谱估计频谱有一半是冗余的缺点，在保证算法计算量增加不大的同时，将频谱分辨率提高了一倍，但频率偏移的存在影响了频率估计精度。针对调制FFT的不足，本文结合频谱修正方法，提出一种谐振式SAW 传感器快速精确的频率估计算法，对谐振式SAW传感器回波信号进行调制FFT计算获取频谱，再使用频谱最大谱线的两相邻谱线取代I_Rife算法频谱细化后的谱线，估算频率偏移因子，对频率估计进行修正。

1 SAW传感器快速频率估计算法

1.1 调制FFT算法原理

调制FFT算法是针对时间长度为T的N点实序列，首先通过时域调制实现频谱搬移，使频谱不再具有对称性，然后对时域调制后的实序列进行FFT变换，最后根据实序列频域的对称性进行倒序插值，重构出N条独立的谱线表示原始实序列的正频率成分[8]。

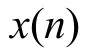
与直接FFT频谱的对应关系为[8]

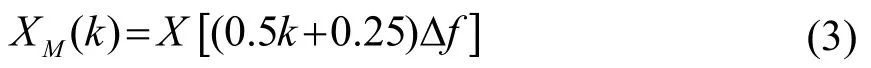
1.2 快速频率估计算法

谐振式SAW传感器的回波信号是由一段等幅值的正弦信号和一段指数衰减的正弦信号组成的混合信号，其频率特性主要受等幅振荡正弦信号持续时间的影响，衰减因子对回波信号频谱的影响可以忽略不计[9]。对等幅振荡正弦信号x（n）进行N点采样，获取离散时间信号序列：

其中：A为信号的振幅，f0为信号的频率，fs为信号的采样频率，φ为初相位。根据式（3）与N点离散傅里叶变换（Discrete Fourier Transform,DFT）公式，计算式（4）的调制FFT频谱为

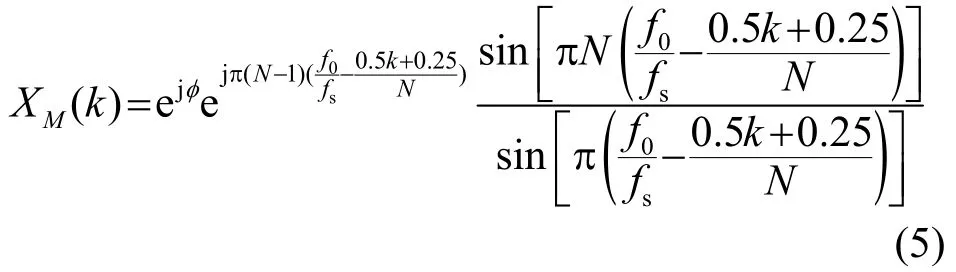
最终求得估计频率为

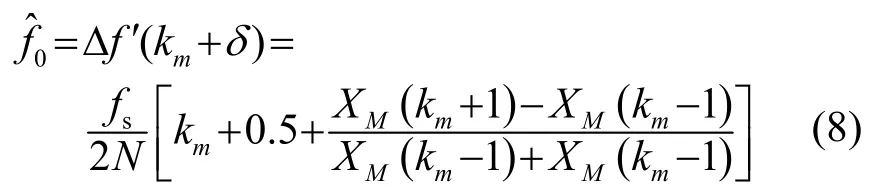
2 计算量分析

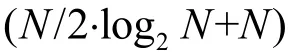
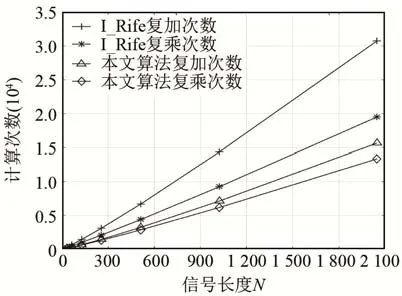
图1 两种算法计算量与信号长度关系Fig.1 The relationship between the calculation amounts of two algorithms and the signal length

3 性能仿真分析

根据现有谐振式SAW传感器参数，取SAW传感器中心频率为fSAW=4 33 MHz，品质因数为Q=10 000。在信号接收端，433 MHz的回波信号经过两次下变频后频率下降到1 MHz附近，工作频率在1 MHz±0.3 MHz范围内。设定信号采样频率为fs=3.125 MHz，信号采样点数N=100，此时回波信号的采样时长为32 μs。为了提高频率分辨率，将信号补零到512点再进行调制FFT变换，此时频谱分辨率为Δf′=3.0 518 kHz。取SAW传感器回波信号频率为f0=320Δf′=976.362 5 kHz，当回波信号正常接收时，其等幅占比在10%～50%之间[9]，取等幅占比30%的回波信号进行模拟仿真，其波形如图2所示。

为了验证本文算法的频率估计速度，将本文算法与I_Rife算法在不同信号长度下使用Matlab软件进行10 000次仿真实验，取频率估计平均运行时间进行对比，结果如图3所示。

由图3数据可知，在信号长度较小时，算法运行时间很短，此时Matlab软件统计时间误差较大，随着信号长度的增加，统计时间较算法运行时间相对误差减小，此时随着信号长度的增加，本文算法较I_Rife算法计算量优势逐渐增大，与理论分析吻合。当N=512时，本文算法的运算速度是 I_Rife算法速度的2.5倍，与理论分析结论一致。

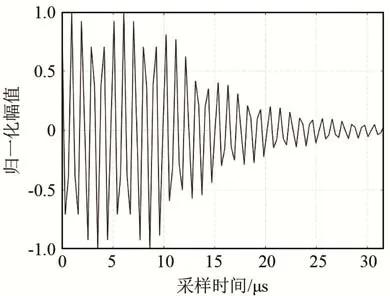
图2 SAW模拟回波信号（f0=976.362 5 kHz）Fig.2 Simulated SAW response signal（f0=976.362 5 kHz）

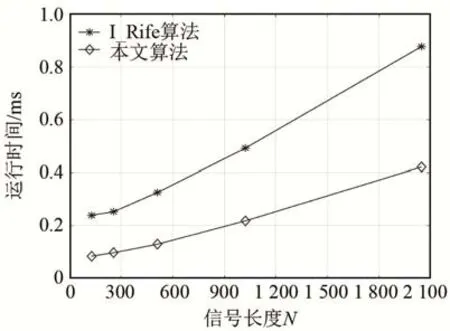
图3 两种算法运算时间与信号长度关系对比Fig.3 Comparison of the relationships between the running times of two algorithms and the signal length

为了验证本文算法对SAW传感器的频率估计性能，在不同信噪比（Signal Noise Ratio,SNR）下，对SAW模拟回波信号f0进行1 000次重复仿真实验，计算频率估计的均方根误差，与I_Rife算法进行对比，结果如表1所示。

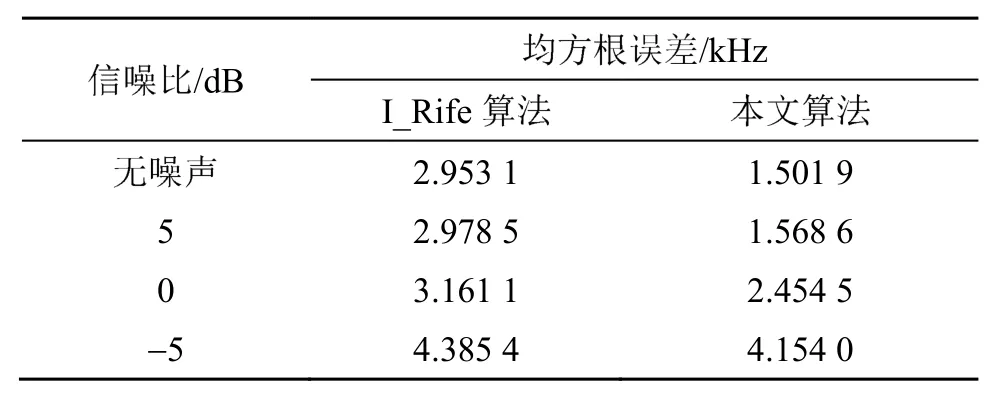
表1 在不同信噪比下两种算法的频率估计均方根误差对比Table 1 RMSEs of frequency estimation of two algorithms under different SNRs

由表1数据可知，在不同SNR下，本文算法对无频率偏移的SAW回波信号的频率估计精度优于I_Rife算法。

图4 在不同频率偏移因子下两种算法的频率估计均方根误差对比（SNR为−5 dB）Fig.4 RMSEs of frequency estimation of two algorithms under different frequency offset factors （SNR=−5 dB）

为了进一步验证本文算法的可行性，在不同信噪比下，在SAW传感器1 MHz±0.3 MHz工作频带内随机选取1 000个回波信号频率进行1000重复仿真实验，计算频率估计平均的均方根误差，与I_Rife算法进行对比，结果如图5所示。

图5 在不同信噪比下2种算法在1 MHz±0.3 MHz的频率估计均方根误差对比Fig.5 RMSEs of frequency estimation in 1MH±0.3 MHz of two algorithms under different SNRs

图5结果表明，信噪比为−5～21 dB时，在SAW传感器的工作频率带宽内，本文算法的频率估计均方根误差优于I_Rife算法。对不同信噪比下的均方根误差求平均值，本文算法均方根误差的平均值为1.716 9 kHz，I_Rife算法的均方根误差的平均值为2.328 7 kHz，本文算法较I_Rife算法频率估计精度提高了26%，验证了本文算法的可行性。

4 结 论

针对高动态环境下的谐振式SAW传感器快速精确频率估计，提出了一种基于调制FFT的SAW传感器快速频率估计算法。通过算法计算量分析，本文算法较I_Rife算法减少了3N次复数乘法、4（N−1）次复数加法，同时不需要判断修正方向，减小了算法的空间复杂度与时间复杂度。针对SAW传感器回波信号，进行信号长度为512点的仿真实验，本文算法的运算速度是I_Rife算法的2.5倍，同时频率估计精度提高了26%。本文算法在提高SAW传感器频率估计精度的同时，提升了频率估计速度，是一种实现谐振式SAW传感器快速频率估计的新方法。