食饵种群密度服从Gompertz增长率的时滞扩散捕食—食饵模型
2022-01-21陈丹丹陈金琼张道祥
陈丹丹, 陈金琼, 张道祥
(安徽师范大学 数学与统计学院,安徽 芜湖 241002)
引言
生态数学模型可用于实际问题的预测、模拟和优化,其中研究最广泛的是经典的Lotka-Volterra模型[1-5]。Leslie[6]利用矩阵方法分析了Lotka-Volterra模型,所得结果表明捕食者的增长率可以趋向无穷大,而且年龄稳态分布存在负元素,这不符合生物学意义。为此,Leslie假设捕食者的环境容纳量与食饵的数量成正比,首次提出并研究了如下捕食模型[6-7]:
(1)
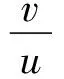
考虑到捕食者对食饵的饱和因素,有学者进一步研究了带有功能反应出数的Leslie-Gower模型[10-11]。张道祥和严平[12]研究了如下的Leslie-Gower捕食—食饵模型:
(2)
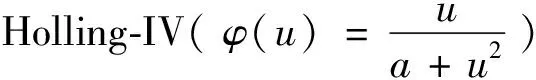

(3)
Lan和Zhu[14]研究了上述系统的Hopf分支和周期解的存在性。

(4)
通过理论分析得到了扩散捕食系统的Turing-Hopf分支存在的条件,并给出了参数曲面上的图灵分支曲线。
上述文章的研究都建立在食饵密度服从Logistic规律的基础上,Gompterz曲线和Logistic曲线的性质比较接近,但在刻画某些食饵密度规律时,Gompterz规律比Logistic规律更贴近实际[18]。因此,本文在文献[17]的基础上,研究了如下食饵种群密度服从Gompterz型增长率的Leslie-Gower时滞扩散系统:
(5)
其中u(t)表示食饵密度,v(t)表示捕食者密度,r,a2分别是食饵、捕食者的内禀增长率,k表示食饵的环境容纳量,a1,b1分别为捕获率和捕食时间,参数b2为捕食者之间的干扰,时滞τ>0描述食饵的妊娠因素。
1 正平衡点的存在性
考虑到系统(5)的生态学意义,这里只研究它的正平衡点。令
则有
定理1.1若满足条件
则系统(5)至少存在一个正平衡点E*=(u*,v*)。
证明由f22(u,v)=0,可知u=v,将u=v代入f21(u,v)=0,则有
令
其中F(u)的定义域为(0,+∞),

2 正平衡点的稳定性和Hopf分支
系统(5)在正平衡点E*=(u*,v*)的线性化方程为:
(6)
其中
a21=a2,a22=-a2
系统(5)在正平衡点E*=(u*,v*)处的特征方程为
λ2+δ1kλ+δ2k+δ3e-λτ=0。
(7)
其中δ1k=-a11-a22+d1k2+d2k2,δ2k=d1d2k4-(a11d2+a22d1)k2+a11a22,δ3=-a12a21。
其中k为波数,我们做以下假设:
H2:a11+a22<0,H3:a11d2+a22d1<0,H4:a11a22-a12a21>0。
定理2.1对任意的k≥0,当τ=0时,若条件H2-H4成立,系统(5)的平衡点E*是渐近稳定的。
证明当τ=0时,特征方程(7)变为
λ2+δ1kλ+δ2k+δ3=0。
我们把特征方程(7)的两个根分别设为λ1,λ2,对任意k≥0,有
λ1+λ2=-δ1k
λ1λ2=δ2k+δ3=d1d2k4-(a11d2+a22d1)k2+a11a22-a12a21。
当条件H2-H4成立,可以得到λ1+λ2<0,λ1λ2>0,即方程(7)有两个负实部的根(两个负实根或一对具有负实部的共轭复根)。因此系统(5)的平衡点E*是渐近稳定的。
接下来,讨论在正平衡点E*=(u*,v*)处的Hopf分支。
设iw是方程(7)的纯虚根,代入方程(7),可以得到
(iw)2+iδ1kw+δ2k+δ3(coswτ-isinwτ)=0。
分离上述方程的实部和虚部,可以推出
-w2+δ2k=-δ3coswτ,
(8)
δ1k=δ3sinwτ。
(9)
根据诱导公式,方程(8)和方程(9)相加可得
w4+(δ1k2-2δ2k)w2+δ2k2-δ32=0。
(10)
令w2=z,则方程(10)变为
z2+(δ1k2-2δ2k)z+δ2k2-δ32=0。
(11)
下面,作如下假设
H5:a11d1+a22d2<0;
H6:a11a22+a12a21>0;
H7:a11a22+a22a21<0。
定理2.2对任意的τ>0,k>0时,若条件H3-H6成立,方程(11)有两个负实部的根,则系统(5)的平衡点E*是局部渐近稳定的。
证明设方程(11)有两个根z1k,z2k,由根与系数的关系,则有
z1kz2k=(δ2k+δ3)(d1d2k4-(a11d2+a22d1)k2+a11a22+a12a21),
z1k+z2k=2δ2k-δ1k2=-(d12+d22)k4-a112-a222+2(a11d1+a22d2)k2。
由定理2.1可知,当条件H3,H4成立,则δ2k+δ3>0;当H5成立时,z1k+z2k<0;当条件H3,H6成立时,z1kz2k>0。
综上所述,当条件H3-H6成立,方程(11)有两个负实部的根,得证。
定理2.3当k=0,条件H4,H7成立时,方程(11)有唯一的正实根
证明当k=0,方程
z2+(δ102-2δ20)z+δ202-δ32=0,
则方程(11)的两个根z1,z2的关系为
z1+z2=-a112-a222,
z1z2=(a11a22-a12a21)(a11a22+a12a21)。
当H4,H7成立,z1z2<0,方程(11)有唯一的正实根z。再由求根公式,方程(11)的根为
定理2.4当k=0,w02-δ20>0时,系统(5)在τ=τ0j处发生Hopf分支,
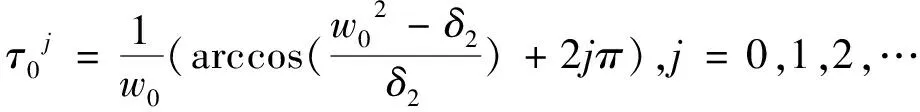
证明当k=0,由方程(8),可得
因此可以求得
注1显然,数列{τ0j}是单调递增的,τ0={minτ0j,j=1,2,…}=τ00。
(12)
而
将上式代入(12)中,可得
(13)
又将前面的τ0j代入(13)中,则有
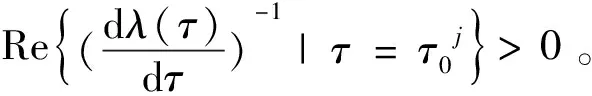
定理2.5对于系统(5),假设条件H2-H4,H7成立,则有
(1)当τ∈[0,τ0),系统(5)的平衡点E*是局部渐近稳定的;
(2)当τ∈[τ0,+∞),系统(5)的平衡点E*是不稳定的。
3 数值模拟
使用Matlab进行数值模拟,验证所得到的结论。在所有数值算例中,固定时间步长Δt=0.01,空间步长Δx=1初始条件是随机的。由于食饵和捕食者的空间斑图是类似的,所以在接下来的数值模拟中仅给出食饵的空间斑图。
3.1 验证平衡点稳定性的条件
首先讨论没有时滞的情形。设系统(5)的参数τ=0,a1=0.7,a2=0.5,r=5,b2=0.2,b1=0.3,K=0.5284,d1=0.01,d2=0.1,选取的参数值满足定理1.1的条件,计算得出平衡点E*=(0.5,0.5)。图1展示的是系统(5)在上述参数下食饵和捕食者的密度分布图。从图中可以看出在初始时刻时食饵和捕食者的密度在一维空间x轴上是随机分布的,但随着时间的增长,食饵和捕食者的密度在空间上均趋于常数值0.5,即趋于系统(5)的平衡点数值。这正好验证定理1.1的结论,即系统(5)的平衡点E*是局部渐近稳定的。

图1 系统(5)参数τ=0,a1=0.7,a2=0.5,r=5,b2=0.2,b1=0.3,K=0.5284,d1=0.01,d2=0.1。
其次,讨论具有时滞效应的情形。图2显示的是不同时滞条件下食饵和捕食者密度随时间变化的演化图,其中每个图的左边子图(a)的参数τ=3,右边子图(b)的参数τ=6,其余参数不变。可以验证,这些参数满足定理2.2中的条件,即此时系统的平衡点是局部渐近稳定的。图2的数值结果验证了理论结果的正确性。
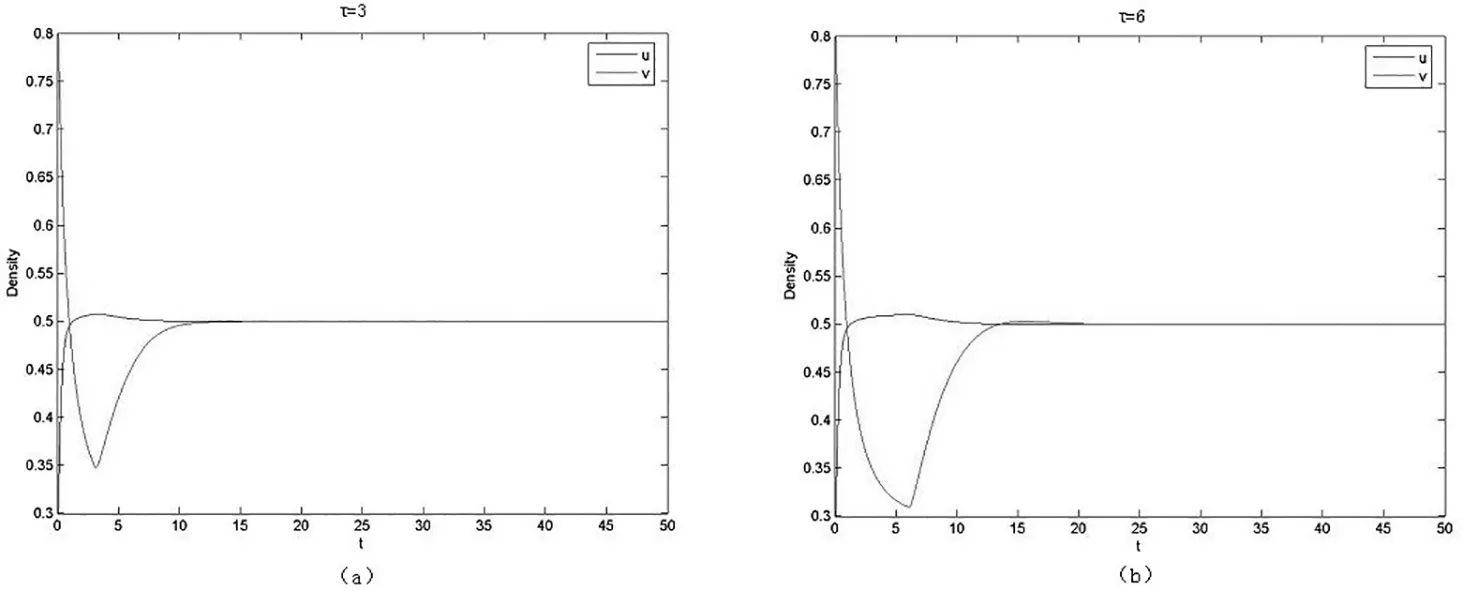
图2 系统(5)参数a1=0.7,a2=0.5,r=5,b2=0.2,b1=0.3,K=0.5284,d1=0.01,d2=0.1。
3.2 时滞对空间斑图形成的影响
当系统(5)的参数选取为a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,d1=0.01,d2=0.1验证满足定理2.5的条件H2-H4和H7时,求得系统的平衡点为E*=(3.6,3.6)以及时滞τ0=0.9686。由定理2.5可知,当取τ=0.05<τ0,系统的平衡点是局部渐近稳定的。图3显示食饵和捕食者的密度随着时间的增长,在空间上都会趋于稳定的数值(平衡点数值)。而当τ=2>τ0,系统的平衡点会变得不稳定。从图4(τ=2),可以看出螺旋波斑图刚刚出现(t=0.1),随着时间逐渐增大,螺旋波慢慢形成,在t>3.3后螺旋波完全展现在空间上,甚至出现了多个螺旋波的空间斑图。这个空间演化过程也反映了系统(5)具有丰富的空间斑图形态。图3和图4显示的结果与理论结果也是吻合的。
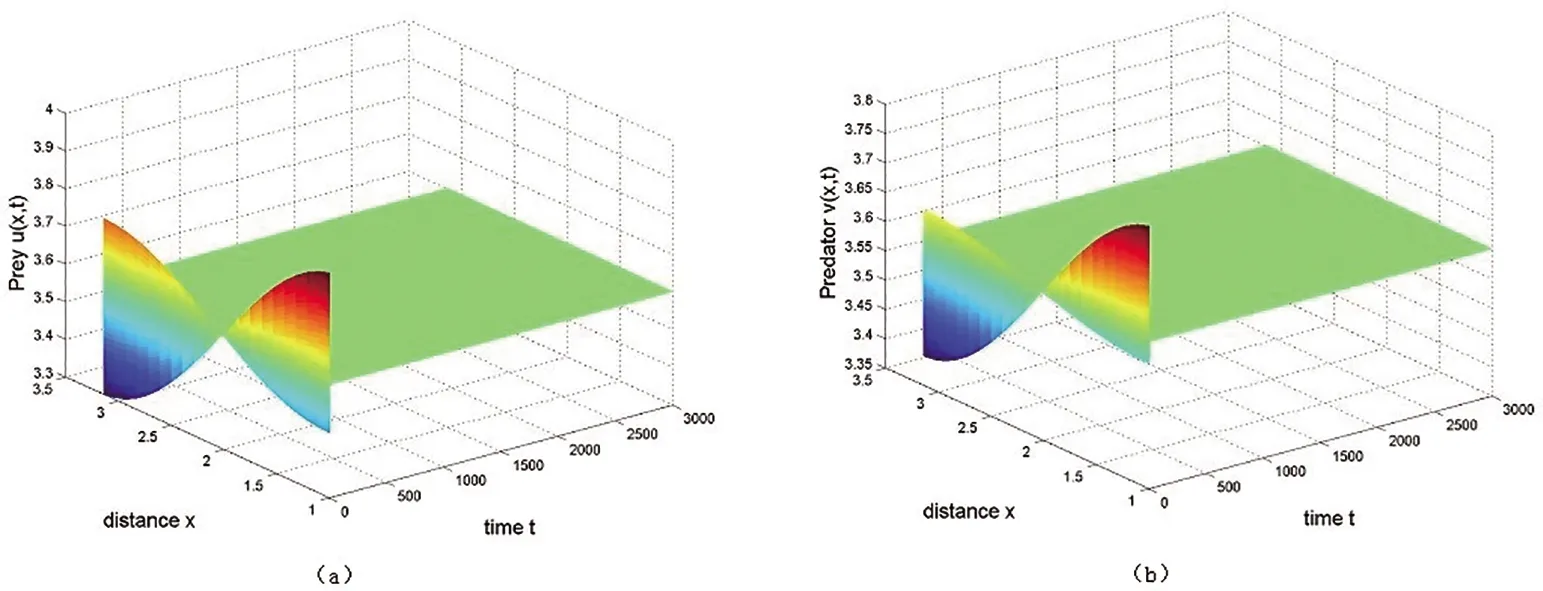
图3 系统(5)参数a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,d1=0.01,d2=0.1。
图5展现的是仅仅改变时滞τ的数值,时间t=3000的空间斑图形态,其他参数同图4。由第一个子图(τ=1),第二个子图(τ=1.5)可以看出斑图形态都是混沌状态,第三个子图(τ=2)显示空间斑图是多个螺旋波,第四个子图(τ=4)的空间斑图是一个螺旋波斑图。这说明在t=3000时,随着τ的增大,食饵的空间分布由混沌变得稳定。
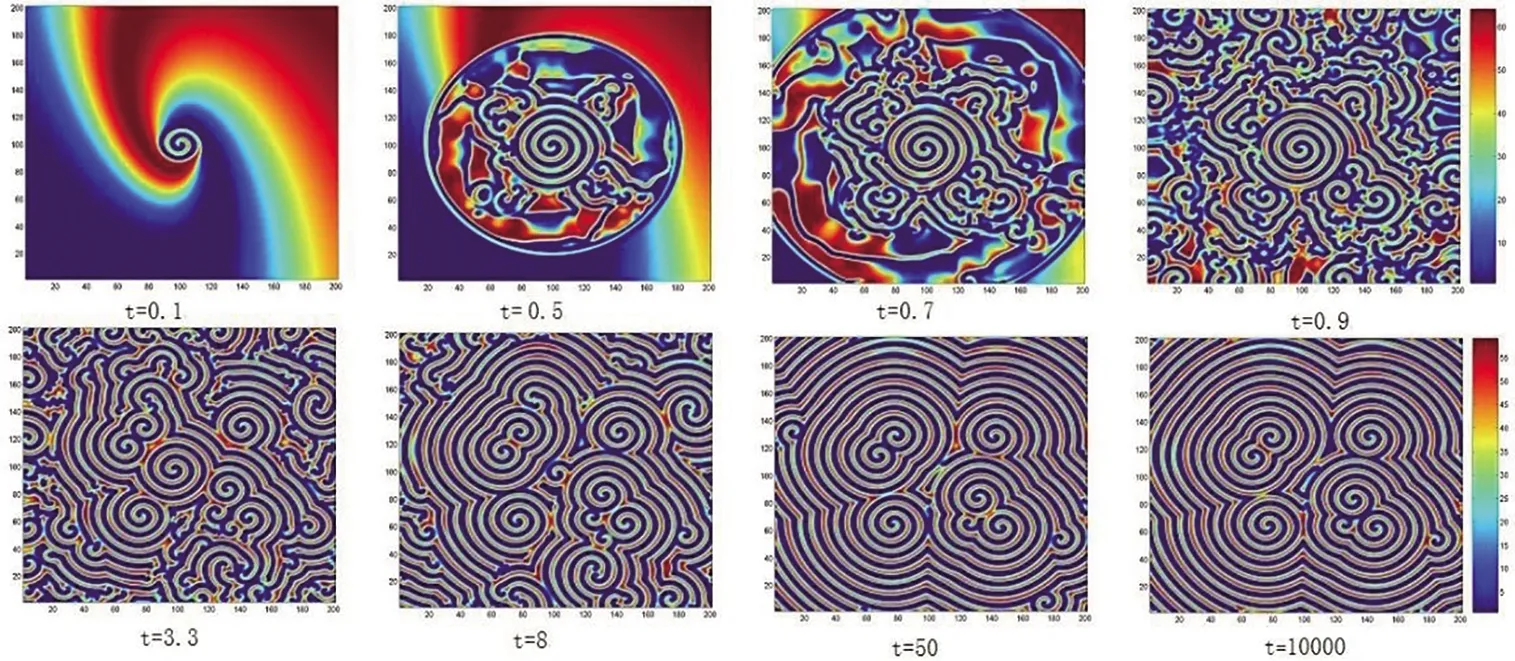
图4 食饵的螺旋波斑图,其中参数a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,d1=0.01,d2=0.1,τ=2。
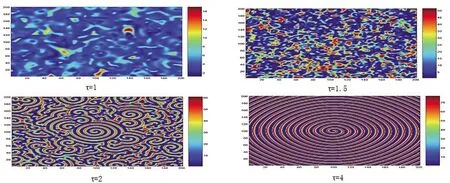
图5 食饵的螺旋波斑图(变化的时滞τ,a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,d1=0.01,d2=0.1。
3.3 扩散系数d2对空间斑图形成的影响
图6是不同扩散系数d2的空间斑图,系统(5)的参数分别为a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,τ=1.5,d1=0.01,d2=0.1。在图6中,第一个子图取d2=0.1,可以看出斑图形态是混沌状态,第二个子图取扩散系数d2=0.5,图像显示螺旋波在慢慢地形成。随着扩散系数d2参数的增大,直至第四个子图(d2=1)展示的是一个螺旋波斑图。这说明随着d2的增大,食饵的空间分布由混沌变得稳定。图6的数值结果验证了扩散系数d2对系统(5)的空间斑图的影响。

图6 食饵的螺旋波斑图(变化的扩散系数d2),
3.4 食饵的增长率r对空间斑图形成的影响
图7展示的是在不同增长率r条件下的食饵密度的空间斑图,此时系统(5)的参数取为a1=2.5,a2=0.45,r=1,b2=0.3,b1=0.1,K=86.7,d1=0.01,d2=0.1,τ=1.5。在图7中,第一个子图参数为:r=1.2304,可以看出斑图形态是混沌状态;第二个子图(r=1.6006)和第三个子图(r=1.8140)均显示斑图为混沌状态;第四个子图r=1.8554表示的是螺旋波斑图,而且它的螺旋波个数不止一个。这说明随着r的增大,在t=3000时食饵的空间分布由混沌状态变得稳定。图7的数值结果验证了增长率r对系统(5)空间斑图的影响。
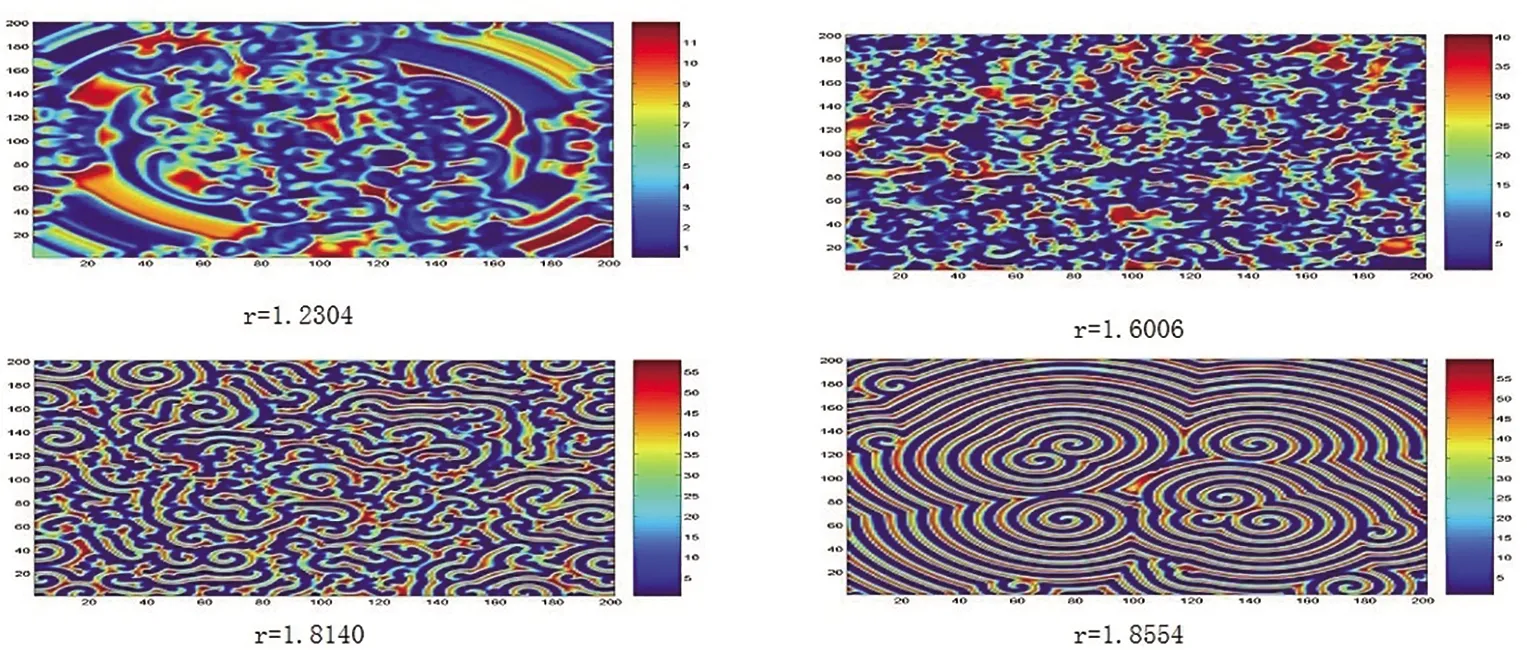
图7 食饵的螺旋波斑图(变化的扩散系数r),
4 总结
本文主要探讨含有Gompertz增长率的扩散捕食生态系统,研究结果表明此系统具有丰富的空间动力学特性:
(1)理论结果表明在一定条件下带有时滞的生态系统存在正平衡点,并且以时滞τ为分支参数,获得了系统的Hopf分支存在的充分性条件。
(2)数值结果表明食饵的增长率、时滞和扩散系数都会影响系统的空间斑图,即在一定的参数条件下,系统会展现不同类型的斑图形态,比如单个螺旋波,多个螺旋波的斑图,甚至出现混沌斑图。
