非线性光学中耦合的高阶Schrödinger方程的有理周期解
2022-01-21王媛
王 媛
(山西能源学院 强基学院,山西 晋中 030600)
引言
近年来,电磁波在非线性介质中的传播引起了非线性物理学家和数学家的关注,尤其是以局部脉冲即孤子形式通过光纤介质的传播。例如,非线性介质中缓慢变化的电磁波可由标准的非线性Schrödinger(NLS)方程描述,该方程也出现在各种物理系统中,例如水波、等离子体物理、固态物理等[1-3]。
关于光纤中光孤子性质的另一个有趣的事实是观察到了高阶效应,而这种效应不能用标准的NLS方程来描述,这种高阶效应的一个例子是存在于孤子光谱中的拉曼过程。因此,Kodama 和Hasegawa提出了一个带有高阶效应的广义高阶非线性方程(HNLS)[4],随后,许多科研人员从不同的方向分析研究了高阶光纤孤子方程。比如:田晋平,Amarendra,Sarma,Azzouzi等用数值模拟方法分别求解了不同的高阶光纤孤子方程(组);田播、高以天团队用双线性、Bell多项式、AKNS系统、Darboux变换、Lax对、渐近分析及线性稳定性分析等方法,对一些光纤孤子方程的孤子解、畸形波解及其传播和相互作用进行了分析和研究[5-11]。
但是,由于问题的复杂性,高阶耦合的非线性Schrödinger方程研究的还比较少。因此,本文考虑如下广义耦合的高阶非线性Schrödinger方程[12]:
(1)
其中α1,α2,α3分别表示线性色散系数,Kerr系数,拉曼散射系数。
Porsezian K等人研究了此方程的潘勒韦可积性,但是对此方程的求解还没有研究过,因此,本文主要利用改进的辅助方程展开方法[13]研究方程(1)的有理形式的周期解。
1 广义耦合高阶非线性Schronger方程(1)的有理周期解
为了寻找方程(1)形式丰富的周期解,假定方程(1)有如下形式的精确解
q1(x,t)=φ1(ξ)eiη,q2(x,t)=φ2(ξ)eiη
ξ=kx+ωt,η=λx+μt,
(2)
其中φ1(ξ),φ2(ξ)是待定的实函数,k,ω,λ,μ是待定实参数,将(2)代入(1)并分离实虚部可得
(3)
由齐次平衡法,假定方程(3)有如下形式的解
φ1(ξ)=a0+a1F(ξ),φ2(ξ)=c0+c1F(ξ),
(4)
其中F(ξ)满足
F′2(ξ)=h0+h1F(ξ)+h2F2(ξ)+h3F3(ξ)+h4F4(ξ)。
(5)
将(4)及(5)代入(3),提取F(ξ)的系数并令其为0,得到22个代数方程,解此方程组并利用方程(5)的解,得到了方程(1)13种类型的有理形式的周期解。
定理依据方程(1)所满足的条件,13种类型有理形式的周期解如下,其中参数m(0 1) a1,α1,ε,k为任意常数。 2) 3) 4) a1,α1,ε,k为任意常数。 5) a1,α1,ε,k为任意常数。 6) a1,α1,ε,k为任意常数。 7) a1,α1,ε,k为任意常数。 8) 9) 10) 11) 12) 13) 当雅克比椭圆函数的模m→1,定理中解2)、3)、6)可退化成如下形式的精确解: 本文主要应用改进的辅助方程展开方法,并利用计算机软件Maple,对一类广义耦合的高阶非线性Schrödinger方程进行了研究,在一定的参数条件约束下,得到了广义耦合的高阶非线性Schrödinger方程13种类型有理形式的周期解以及其对应的3种形式的孤子解。据我们所知,这些解在已有的文献中没有出现过。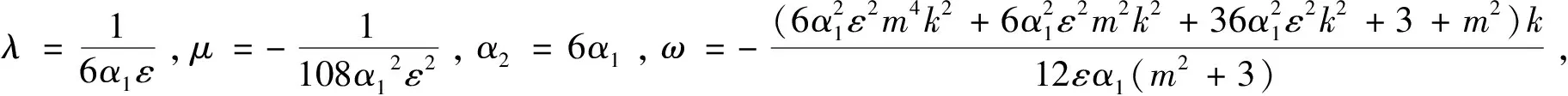
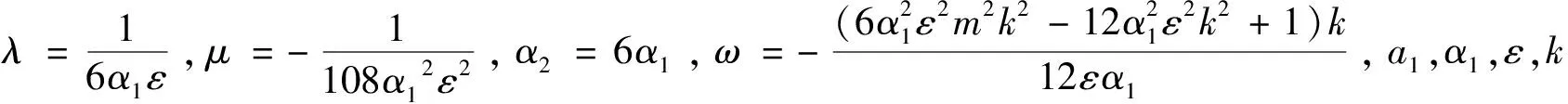
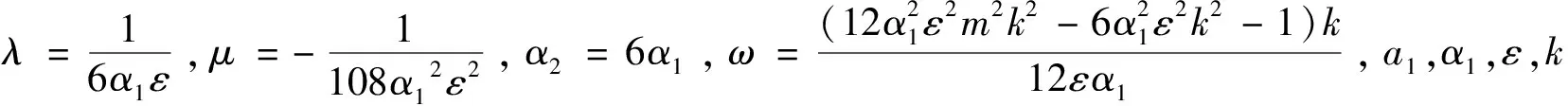

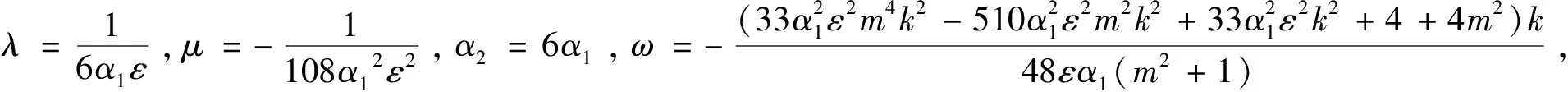
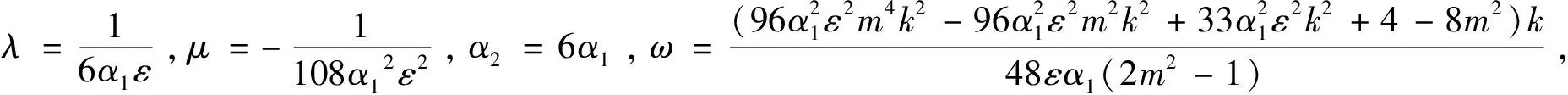
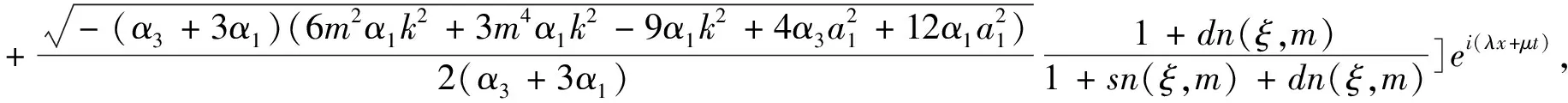
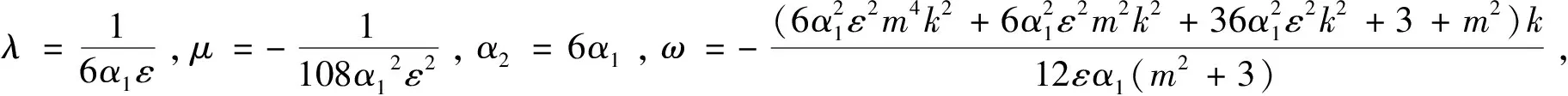
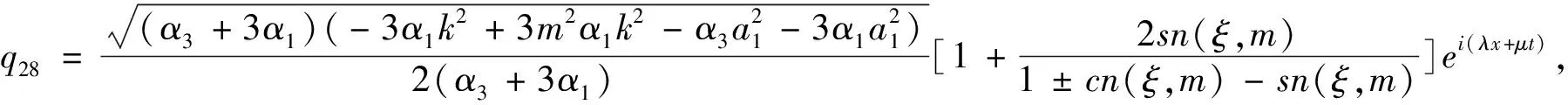
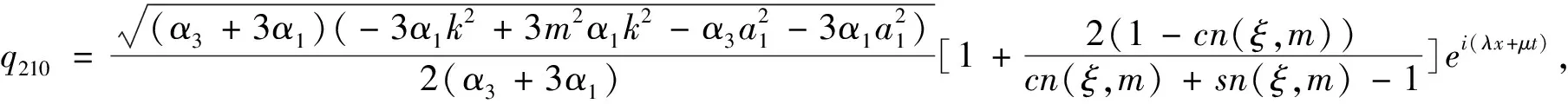
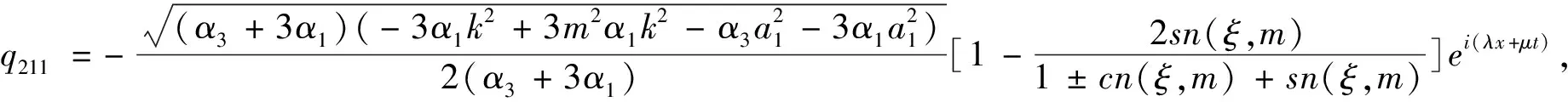
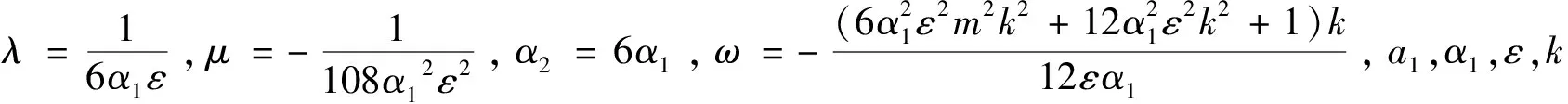
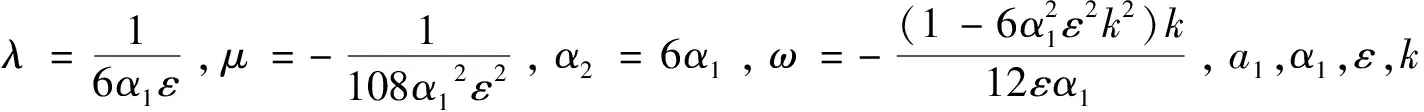
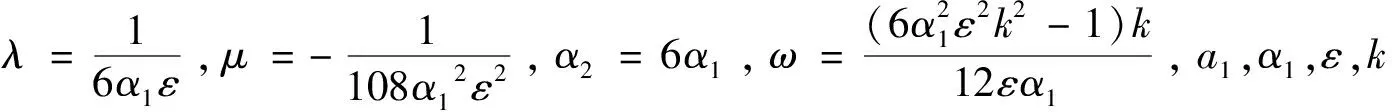
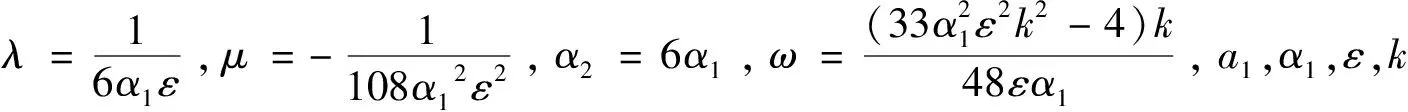
2 结论
