考虑价格和时间敏感性需求的两周期供应链鲁棒优化模型

孙艺萌，邱若臻，高亚楠

(东北大学 工商管理学院，辽宁 沈阳 110169)

科技的发展、市场的更新和消费者偏好的变化，使得手机、笔记本电脑等电子产品和流行服饰、潮流手包等时尚产品在火热销售后迅速大幅降价。新产品的出现降低了原产品对顾客的吸引力，使消费者不愿以原价购买该产品。而新产品售价较高，性能有待检验，口碑有待肯定，所以仍有很多消费者愿意以折扣价格购买原产品。因此，上述电子产品和时尚产品具有生命周期短，需求不确定性高的特点[1-2]。一方面，原产品未来的降价趋势和较大的需求波动使得零售商倾向于减少库存和推迟订货[3]。因此，在较短的生命周期内根据实时市场需求信号制定双定价订货策略成为趋势。同时，制造商为维持自身利润，也会采取相应价格措施来支持零售商的价格策略。另一方面，新产品的出现使得原产品需求量减少，在有限的市场份额中，原产品零售商不得不降价以维持需求量，即随着原产品过时，需求的价格敏感性增加。因此，上述产品的市场需求同时具有价格和时间敏感性特征。据此，本文在不确定需求下考虑需求的价格和时间敏感性特征，以利润最大化为目标，解决制造商的两阶段定价和零售商的两阶段定价和订货问题。

一些学者已经对双订货决策或双定价决策或其同时决策问题进行研究。对于双订货决策问题，Taylor[4]在零售价格下跌环境中建立由一个制造商和一个零售商组成的双订货决策模型，验证了价格保护、销售中期退货和销售末期退货3种策略的结合能够获得供应链协调，实现双赢局面。Ma等[2]针对具有长提前期和短销售期的时尚品供应链，为风险厌恶型零售商建立了双订货机会模型。其中，第一次订货决策是基于零售商对需求的初始预测；随着销售季节的来临，市场需求信息更加完善，零售商更新需求预测并进行第二次订货。Khouja等[5]为折扣品零售商建立了双采购机会模型。其中，第一次采购发生在当前销售季的期末，即折扣品零售商从品牌零售商和制造商处购买剩余库存并储存到下一销售季；第二次采购发生在下一销售季的期初，即折扣品零售商根据市场需求信息补充库存，补充库存来源为品牌零售商和制造商的预期剩余库存、超量生产产品、不规则产品或退货再包装产品。对于双定价决策问题，Zhang等[6]考虑季节性产品在销售期内易降价的特点，建立两阶段二级供应链定价决策模型，分析消费者参照价格效应和供应链快速响应能力对制造商和零售商的定价决策以及利润的影响。Shum等[7]考虑产品由于生产学习效应和技术进步效应引起的成本降低以及策略型消费者对于降价的预期，在成本降低幅度不确定环境下，建立两阶段动态定价、价格承诺和价格匹配模型，并将3种定价模式进行对比。对于双订货和定价同时决策问题，Herbon等[8]将报童产品销售季分为两个子周期进行3阶段决策，研究零售商的订货和推迟定价问题。第一阶段为第一期销售开始前，零售商决定第一期订货量；第二阶段为第一期，其中，第一期期初，零售商根据市场需求信号制定第一期定价，第一期期末，零售商决定第二期订货量；第三阶段为第二期期初，零售商更新市场需求信号制定第二期定价。

然而，以上考虑双定价订货策略的文献缺乏对于零售商双定价、双订货决策以及制造商定价决策三者的同时考虑。而对于以制造商为主导的二级供应链中，制造商批发价格严重影响着零售商的定价和订货决策以及零售商和供应链整体的利润。因此，本文将以零售商和制造商利润最大化为目标，考虑制造商在第二阶段降低和维持批发价格两种情况，制定零售商双定价和双订货决策以及制造商(双)批发价格决策。

对于价格和时间敏感性需求，学者们主要在价格与时间对需求影响的乘法效应和加法效应下构建需求函数。在乘法效应下，Maihami等[9]在缺货被部分积压的条件下，研究非瞬时变质物品的联合定价和库存模型，模型中物品需求率与价格线性相关，与时间指数相关。Avinadav等[10]假定没有缺货积压，针对具有确切保质期的易逝品建立最优定价、订货量、补货周期模型，其中需求率随价格线性递减，随补货后库存时间多项式递减。San-José等[11]假定缺货被全部积压，建立以定价、最大库存量和补货周期为决策变量的库存模型，其中，需求是关于价格的Logit函数，是关于时间的幂函数。在加法效应下，You[12]研究易腐蚀品库存系统的联合订货定价决策，其中需求为时间的指数函数，为价格的线性函数。马士华等[13]考虑需求随价格和供应链响应时间的线性递减关系，研究分散与集中决策下的MTO供应链决策问题。杨文胜等[14]在需求与价格和交货期线性负相关下，研究电子市场的交货期定价决策。董毓芬等[15]考虑需求随价格和供应提前期线性递减的关系，建立以制造商供应提前期和批发价格、零售商销售价格为决策变量的两阶段供应链协调模型。Pekgün等[16]考虑需求与价格、提前期以及交叉价格和交叉提前期的线性关系，在分散决策和集中决策下对比了两个竞争公司的定价和提前期决策以及利润。另外，Jadidi等[1]将需求的时间敏感性表示为需求的价格敏感性系数随时间的变化，在零售商一次和两次订货机会下，研究报童产品的两阶段定价问题。

然而，上述文献的研究均假设需求分布是已知的。但现实中，同时具有价格和时间敏感性的需求，其波动频率高，波动幅度大，因此决策者很难获得其真实分布信息。据此，本文在考虑需求的价格和时间敏感性基础上，考虑需求的不确定性特征，建立需求不确定集合，并在此基础上利用鲁棒优化方法获得制造商和零售商最坏情况下的最优利润。

Scarf[17]首次在需求自由分布下，利用最小最大鲁棒建模准则解决报童模型的最优订货量问题。随后，不断有学者利用鲁棒优化方法解决报童产品库存问题。Carrizosa等[18]利用基于需求不确定集合的鲁棒优化方法，以最大化最坏情况收益表为目标，解决具有自回归需求的报童产品库存问题。Abdel-Aallm等[19]在不同的需求不确定集合下，利用鲁棒优化方法为报童产品决策最优订货量并选择所要服务的最优需求集合。Rahimian等[20]利用总离差来构建需求分布的不确定集合并找到最为合适的鲁棒性水平，在此基础上为报童产品建立了以最小化最坏成本为目标的分布式鲁棒优化模型。Bai等[21]采用鲁棒优化方法建立报童模型，解决了再制造系统的联合采购和生产问题。Anh等[22]在已知离散需求的部分分部信息下研究了报童问题。区别于以上单阶段报童问题，本文将利用鲁棒优化模型解决不确定环境下的供应链两阶段定价、订货决策。

1 问题描述

考虑两周期销售环境下由一个制造商和一个零售商组成的二级供应链系统。制造商为零售商提供产品批发，零售商将所订购产品销售至终端市场，并且在每一销售周期期初，零售商各有一次产品定价和订购机会。在产品终端市场，零售商面临不确定市场需求，并且该不确定市场需求具有价格和时间敏感性特征。需求的价格敏感性即由价格变动引起的需求量反方向变动；需求的时间敏感性是指需求的价格敏感性只在一段时间内是恒定的(如产品引入期和发展期)，而随着产品生命周期的发展(如产品进入成熟期和衰退期)以及竞争性新产品的不断涌现，产品吸引力下降，需求的价格敏感性增加。因此，本文根据需求的时间敏感性特征，将产品的销售周期分为两阶段。第一阶段中需求的价格敏感性系数恒定，第二阶段中需求的价格敏感性系数增加。特别地，零售商通常在第二阶段降低销售价格，以避免价格敏感型系数增加而导致需求量下滑。根据上述问题，本文以制造商和零售商利润最大化为目标，在具有价格和时间敏感性的不确定性市场需求环境下，为制造商和零售商制定两阶段最优定价和订货量决策。

产品销售期间，双方以制造商为主方，零售商为从方进行Stackelberg博弈。在销售期期初，制造商首先决策每个阶段的单位批发价格w1和w2；随后，在不确定市场需求D1和D2下，零售商根据制造商的批发价格决策每个阶段产品购买量Q1和Q2以及单位销售价格p1和p2(p2≤p1)。特别地，如果制造商在第二阶段降低批发价格，即w2＜w1，则称所建模型为具有回扣的主从对策模型；如果制造商在第二阶段不降低批发价格，即w2=w1，则称所建模型为不具回扣的主从对策模型。给定制造商单位制造成本cm，假设cm＜w2≤w1＜p1且w2＜p2≤p1。在每一阶段销售期末，若有需求未被满足，则产生单位惩罚成本s；若有产品剩余，则产生单位持有成本为h。

根据文献[23]，为不确定需求定义如下区间不确定集合。

定义1不确定需求Di(i=1,2) 隶属于如下区间不确定集合Ui。

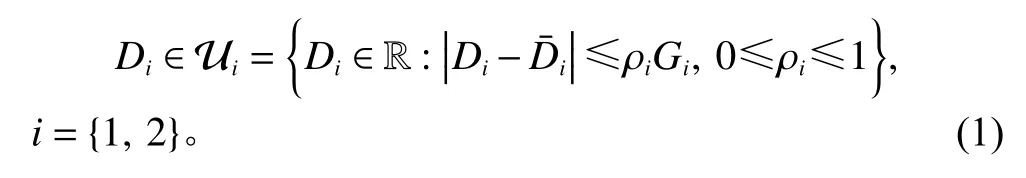
其中，Di为 第i(i=1,2 ) 周期的实际需求；D¯i为决策者估计的名义需求；ρi为 不确定水平；Gi为需求不确定规模，即Di偏 离的最大可能程度。

式(1)描述了每周期内实际需求Di围 绕名义需求i进 行 波动的范围，即−ρiGi≤Di≤+ρiGi(i=1,2) 。通过调节不确定水平ρi的大小，可调节需求不确定集合的范围。ρi越大，需求不确定集合涵盖的不确定性越大，该集合下的定价订货策略对抗不确定性的能力越强。为了反映需求的价格和时间敏感性特征，采用线性需求函数对名义需求i(i=1,2)进行描述，即=A−bp1，=A−(b+θ)p2，其中，A为市场容量；b和 (b+θ)分别为第一周期和第二周期中需求的价格敏感性系数；θ为第二周期中需求的价格敏感性系数增量；A、b和 θ 均为给定参数。

2 集中决策下的供应链鲁棒优化模型

为分析分散决策下的供应链渠道效率，首先引入集中决策下的供应链鲁棒优化模型。在集中决策下，制造商与零售商整合为统一的生产与零售实体，并以整个供应链利润最大化为目标进行定价与订购决策。集中决策下，供应链整体在整个销售期的总利润表示为

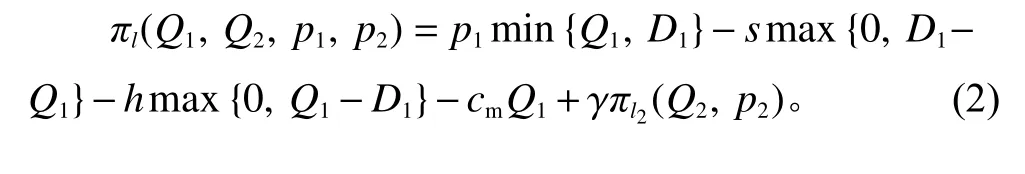
式(2)等号右边分别为供应链整体在第一阶段的销售收入、缺货成本、库存持有成本和产品生产成本，最后一项为供应链在第二阶段的利润现值，其中， γ∈(0,1]为折扣因子。由式(2)可以看出，如果第一销售阶段出现产品剩余，将追加一期库存持有成本。令X=max{0,Q1−D1}为第一阶段期末剩余库存，该部分库存可转入第二阶段进行销售。因此，供应链在第二销售阶段期初订货后可用于销售的产品总量为X+Q2， 则供应链第二阶段利润πl2(Q2,p2)可表示为

式(3)等号右边分别为供应链在第二阶段的销售收入、缺货成本、库存持有成本和产品生产成本。将式(3)代入式(2)可得供应链在整个销售周期的总利润为

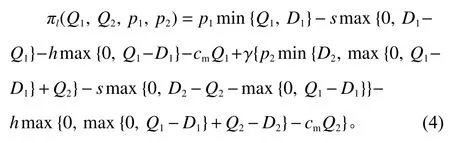
式(4)等号右边含有 min{·}和 max{·}运算，增加了求解难度。为便于模型求解，引入辅助变量α和β ， 并令α =min{Q1,D1}，β =min{D2,Q1−α+Q2}，其中，α 和β 满 足α ≤Q1，α ≤D1， β ≤D2， β ≤Q1−α+Q2。经过代数变换，在整个产品销售期内，式(4)供应链利润最大化问题可描述为如下带有约束的数学规划问题。

式(5)中，Z为替代原目标函数的辅助变量。然而，各销售阶段内的需求D1和D2未知，导致问题(5)难以直接求解。由于不确定需求仅存在于问题(5)的约束中，不失一般性，令F(D1,D2,)≤0表示上述问题(5)中的约束条件，则在需求不确定条件下，问题(5)的鲁棒对应模型可描述为

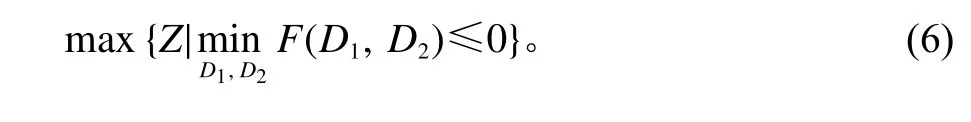
可以看出，如何描述不确定需求是求解上述问题的关键。在需求所隶属的不确定集，即式(1)下，上述问题(6)等价于

通过求解问题(7)，可以得到集中决策下的供应链鲁棒定价、订货决策及对应的系统绩效。下面将进一步讨论分散决策下考虑需求不确定性的两周期供应链决策问题。

3 分散决策下的供应链鲁棒优化模型

集中决策虽然有利于供应链整体利润最大化，却使供应链中部分企业的利润无法达到最优。在市场经济条件下，供应链的上下游企业大多是相互独立的经济实体，并通过分散决策使得自身利润达到最优。在分散决策下，制造商与零售商分别以各自利润最大化为目标进行以制造商为主导的Stackelberg博弈，即制造商作出批发价格决策后，零售商根据该批发价格作出定价与订购决策。

3.1 供应链主从对策鲁棒对应模型

在基本的供应链主从对策模型中，制造商在销售期第二阶段不提供任何回扣，以同样的批发价格向零售商提供产品，即w=w1=w2。不失一般性，将该背景下的供应链策略称为(p1,p2)策略。零售商在整个销售期的利润可表示为

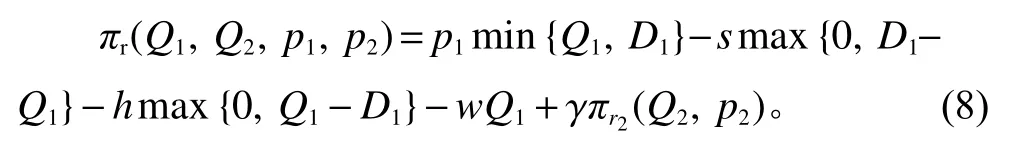
式(8)等号右边前4项分别为零售商在第一阶段的销售收入、缺货成本、库存持有成本和产品批发成本。最后一项πr2(Q2,p2)为零售商在第二阶段的利润，形式如下。

其中，X=max{0,Q1−D1}为第一销售周期期末剩余库存量。将式(9)代入式(8)可得零售商在整个销售期的利润为

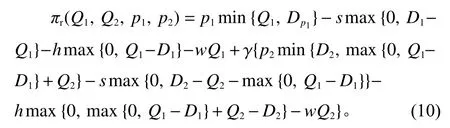
同样地，引入辅助变量 α和 β ，并令α=min{Q1,D1}，β=min{D2,Q1−α+Q2}， 满 足 α≤Q1， α≤D1，β≤D2，β≤Q1−α+Q2。经过代数变换，在整个产品销售期内，式(10)零售商利润最大化问题可描述为式(11)，其中，Z为替代原目标函数的辅助变量。

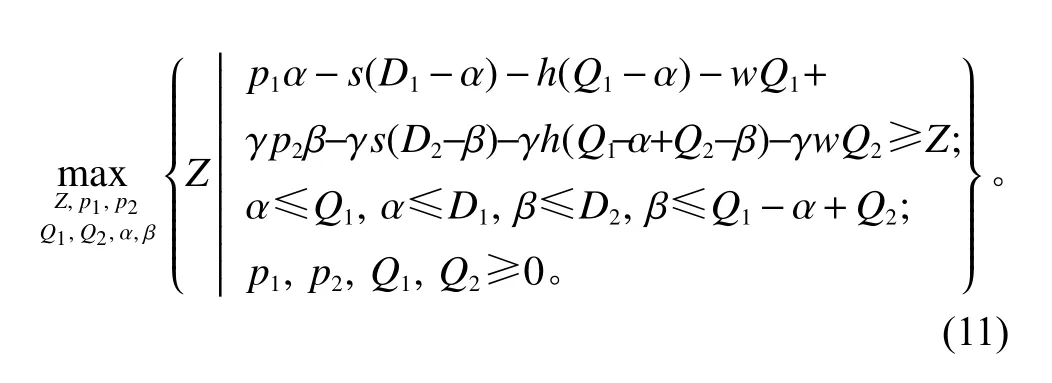
当需求未知时，在式(1)下，遵循与集中决策下问题(5)相同的处理逻辑，零售商优化问题(11)在最坏情况下的鲁棒对应模型可描述为

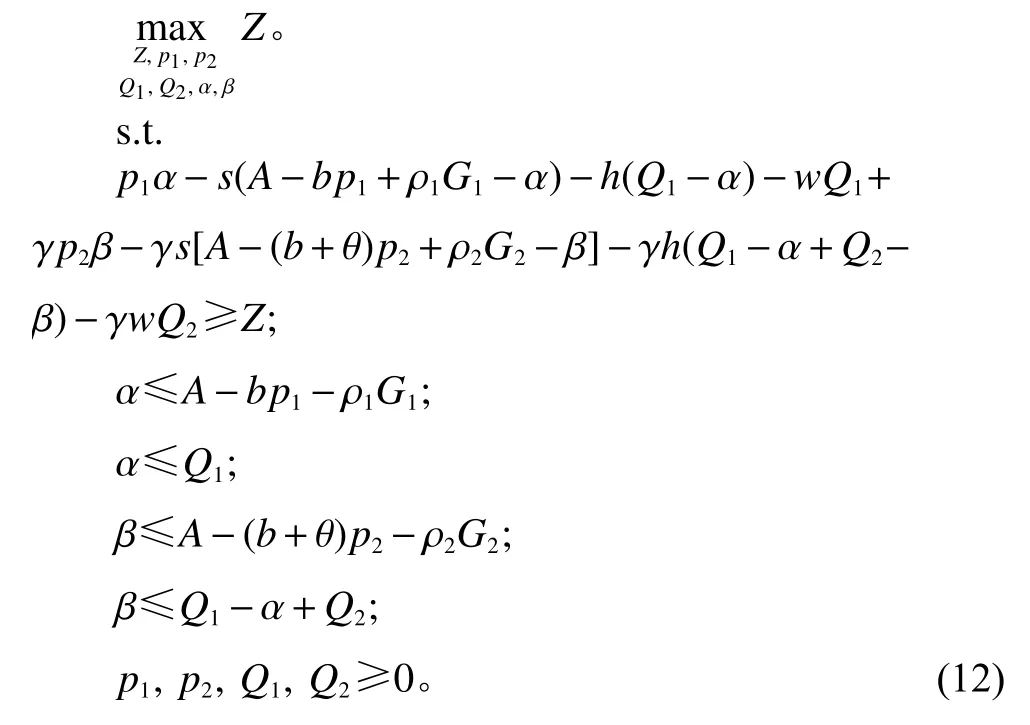
在不考虑回扣的供应链主从对策下，制造商利润最大化问题可表示为

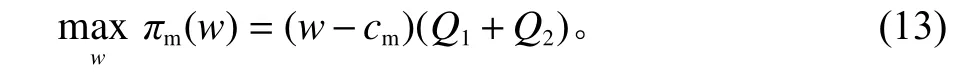
通过求解模型(12)和(13)，获得制造商最优批发价格和零售商最优定价、订货决策。已有研究表明，由于双重边际化效用，基于上述分散决策得到的供应链及成员利润并非最优。下面将进一步探讨制造商通过实施简单的回扣政策，是否能够改进成员双方利润。

3.2 具有回扣的供应链主从对策鲁棒对应模型

在销售期第二阶段，需求的价格敏感性系数增加，表明产品对消费者的吸引力下降。为抑制需求急剧下降，需要零售商降低零售价格，这可能导致零售商利润降低。为了缓解这一问题，激励零售商增加订购量，制造商提供一种补偿政策，即通过降低第二阶段的单位批发价格为零售商提供价格回扣。令 δ表示制造商第二阶段对于单位产品所提供的回扣额度， δ=w1−w2＞0。不失一般性，将具有回扣的供应链决策称为(p1,p2,δ)策略。

在具有回扣的主从对策模型中，零售商在整个销售期的利润可表示为

其中，X=max{0,Q1−Dp1}。式(14)等号右侧前4项的总和为零售商第一阶段的利润，后4项的总和为零售商第二阶段利润。特别地，可将第二阶段批发价格表示为w2=w1−δ。遵循3.1节中的过程，通过引入辅助变量α 和β，则在式(1)所示需求不确定集下，零售商在整个销售期的鲁棒优化问题可表示为

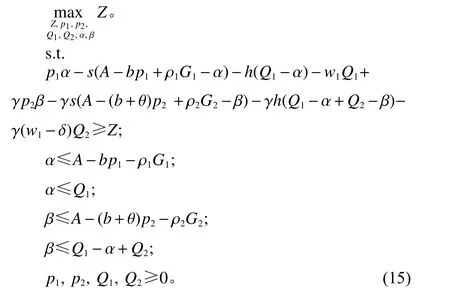
式(15)中，Z为辅助变量。与(p1,p2)策略不同，在具有回扣的供应链主从对策下，制造商问题为确定最优的第一阶段批发价格和第二阶段提供的回扣金额，实现利润最大化，即

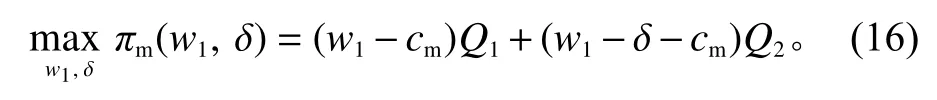
通过求解模型(15)和(16)，可以获得制造商第一阶段的最优批发价格和第二阶段提供的回扣金额，以及零售商在两个销售阶段分别实施的定价和订货决策。下一节中，将通过数值分析探讨不考虑回扣的 (p1,p2)策 略和具有回扣的 (p1,p2,δ)策略对供应链成员决策和利润的影响。

4 数值算例与分析

为验证文中所建集中与分散决策下供应链鲁棒优化模型的有效性，对相关模型进行数值实验，分别分析需求不确定性水平ρ、价格敏感增量θ 对制造商批发价格、零售商销售价格、零售商订货量、双方利润以及供应链总利润的影响，并提出管理启示。模型中的参数赋值如下：A=10，b=0.5，s=5，h=2， γ=1，cm=1，G1=G2=2。

1) 需求不确定性水平ρ对供应链决策和绩效的影响。

表1展示了集中决策下，需求不确定性水平ρi(i=1,2)对供应链定价、订货决策和系统总利润的影响。其中，不确定性水平 ρ1=ρ2={0.0, 0.1, 0.2, 0.3,0.4, 0.5}，价格敏感增量θ =0.1。 特别地，ρi=0(i=1,2)等价于没有不确定性时的情况。ρi越大，表示不确定需求的波动范围越大，不确定程度越高。可以看出，随着需求不确定性水平ρi的增加，供应链总利润πl下降，供应链在各个阶段的定价和订货量决策呈降低趋势。这是因为需求不确定性程度越高，零售商面临的风险越大，为规避需求不确定性带来的风险，零售商选择保守的定价和订货策略，从而降低了供应链总体利润。

表2和表3分别展示了分散决策下，两种不同策略下主从对策鲁棒对应模型所获最优决策和利润随不确定性水平ρi(i=1,2)的变化情况。从表2和表3可观察到以下结果。(1) 随着需求不确定性水平ρi的增加，两种策略下的制造商批发价格w、零售商销售价格pi均呈降低趋势，同时供应链及其成员利润均减少。这是因为需求不确定性水平的增加，使得制造商和零售商选择较为保守的定价策略，以刺激消费者购买，而较低的定价使得双方利润和供应链总体利润减少。注意到当 ρ1=ρ2≤0.4时，零售商订货量Q1和Q2整体呈现下降趋势，而当 ρ1=ρ2=0.5时，Q1和Q2显著回升。这是因为，当需求不确定性水平较小时（即 ρ1=ρ2≤0.4） ，随着ρi的增加，零售商选择更为保守的订货策略，以避免实际需求骤减所带来的库存持有成本，同时亦能减少订货成本；而当不确定水平较大时（即 ρ1=ρ2=0.5），实际需求骤增所导致的缺货成本将远大于实际需求减少所带来的库存持有成本和剩余产品的订货成本之和，因此零售商选择增加订货量来抵御需求的不确定性。(2) 相比于制造商，零售商利润πr随着不确定性水平ρi的增加下降幅度较大。一方面，零售商直接面临着市场需求的波动性，需求波动幅度的增加会导致零售商库存积压成本或缺货成本增加，从而减少零售商利润。另一方面，在各阶段实际需求到来之前，零售商已向制造商订货，因此实际需求波动对制造商利润影响相对较小。(3) 同一不确定性水平ρi下 ，制造商利润大于零售商利润，即πm＞πr。这是因为，制造商为Stackelberg博弈的主方，零售商为从方，即制造商首先作出最有利于自身利润的批发价格，而该批发价格对于零售商并不是最优的。(4) 对比表1可知，分散决策下的供应链总利润小于集中决策下的供应链总利润，即 (πm+πr)/πl＜1。这一结果表明分散决策下，制造商和零售商的最优决策无法获得供应链协调。然而，相对于不考虑回扣时的情况，适度的回扣政策将改进供应链成员双方的利润绩效。

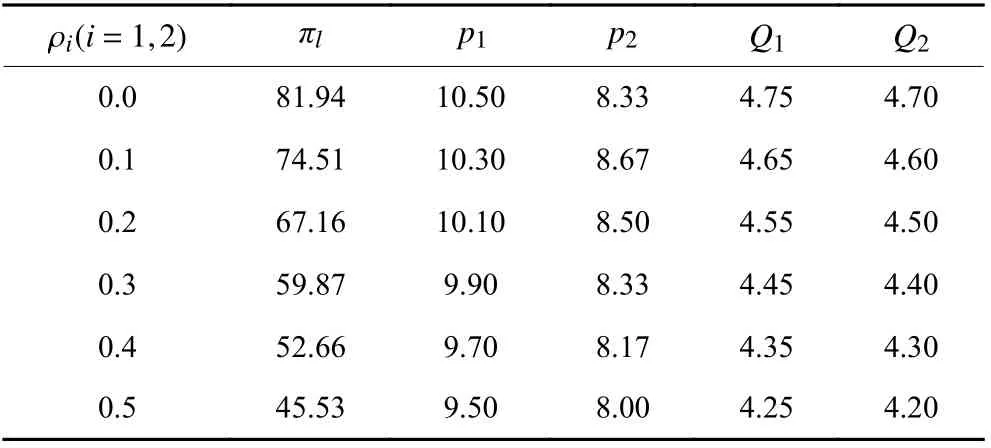
表1 集中决策下的供应链鲁棒对应模型最优决策 (θ =0.1)Table1 The optimal decisions of the robust counterpart under centralized decision(θ =0.1)

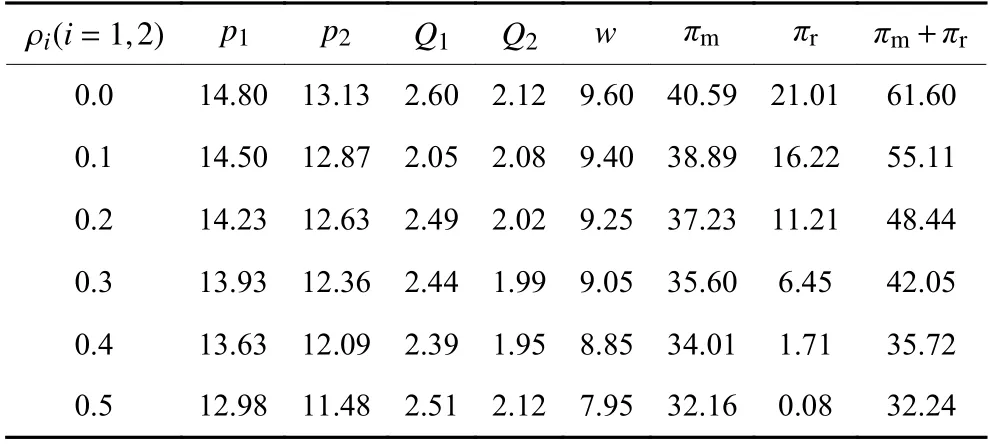
表2 不具回扣的主从对策鲁棒对应模型最优决策 (θ =0.1)Table2 The optimal decisions of the robust counterpart without rebate (θ =0.1)

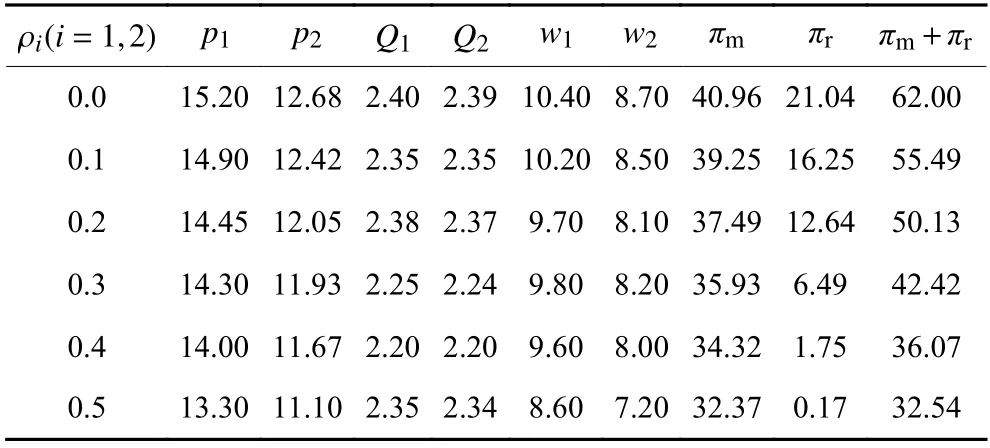
表3 具有回扣的主从对策鲁棒对应模型最优决策(θ =0.1)Table3 The optimal decisions of the robust counterpart with rebate (θ =0.1)

在不具回扣的主从策略 (p1,p2)和具有回扣的主从策略(p1,p2,δ)下，图1分别对比了需求不确定性水平ρ对制造商利润、零售商利润以及总利润的影响。由图1可知，制造商在需求的价格敏感度提升时给予零售商回扣，将有利于所有供应链成员及系统利润的增加。

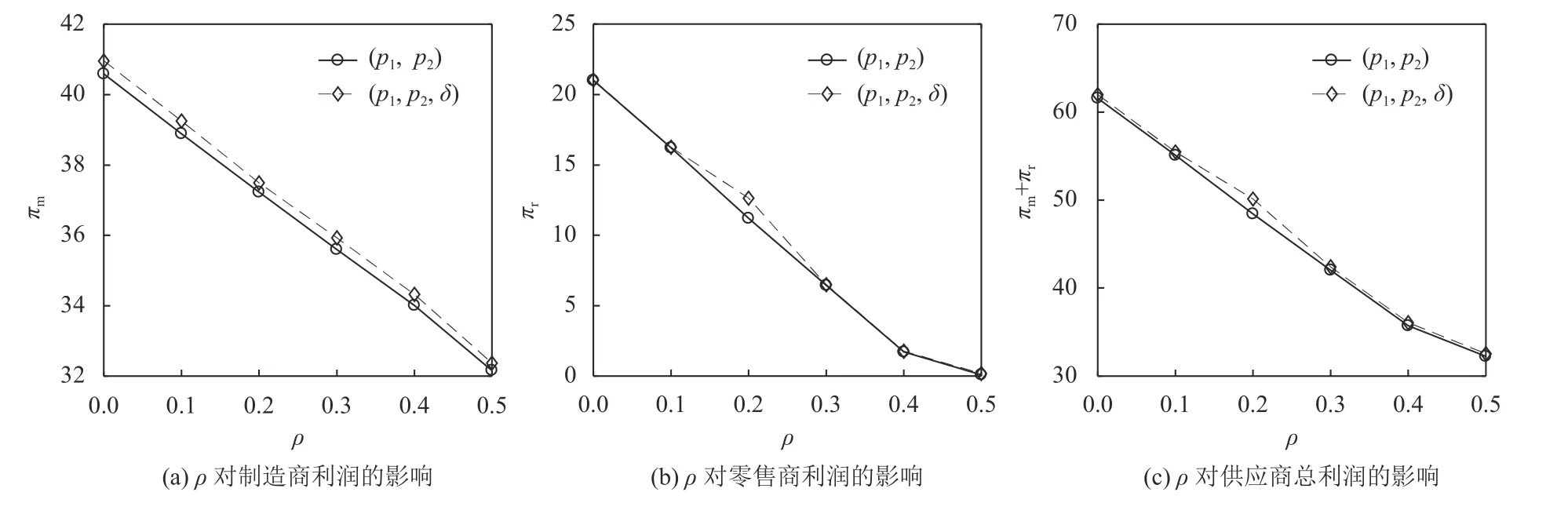
图1 两种策略下制造商利润、零售商利润和系统总利润对比Figure1 Profit comparison of the manufacturer, the retailer and the supply chain

2) 需求价格敏感性增量 θ对运作决策和绩效的影响。

表4和表5分别展示了 (p1,p2)和 (p1,p2,δ)两种策略下，价格敏感增量 θ对零售商和制造商最优决策及利润的影响。一般情况下，价格敏感增量不大于价格敏感系数，即 θ≤b， 因此设定θ={0.1, 0.2, 0.3,0.4, 0.5}，同时固定不确定性水平为 ρ=ρ1=ρ2=0.1。

由表4和表5可得如下结论。(1) 随着 θ的增加，零售商定价pi和制造商批发价格w降低。这是因为，当需求对于价格的敏感性增加时，零售商通过降价来减缓需求量下滑，而为了支持零售商的降价策略，制造商也降低其批发价格。(2) θ增加时，零售商总订货量由于需求的下降而减少。表4表明，在不具回扣的主从策略下，零售商第一周期订货量Q1增加，而第二周期订货量Q2减少。后者是因为，第二周期需求的价格敏感度(b+θ)增加导致该期名义需求减少；前者是因为，在第二周期名义需求减少时，零售商希望通过增加第一周订货量来满足更多第一周期需求。同时， θ增加时，表5表明，在具有回扣的主从策略下，零售商两周期订货量之和(即Q1+Q2)增加。该结果说明制造商的回扣策略能够有效鼓励零售商增加订货量。(3) θ增加时，制造商利润和总利润降低。(4) 通过表4还可发现，随着 θ的增加，制造商给予零售商更高的回扣δ =w1−w2。这是因为 θ增加时，零售商的降价幅度(p1−p2)变大，因此制造商给予零售商更多的回扣来鼓励零售商订货。(5) 对比表4和表5中制造商利润πm和零售商利润πr可 知，制造商和零售商均在 (p1,p2,δ)策略下获利更多，与图1结果相符。

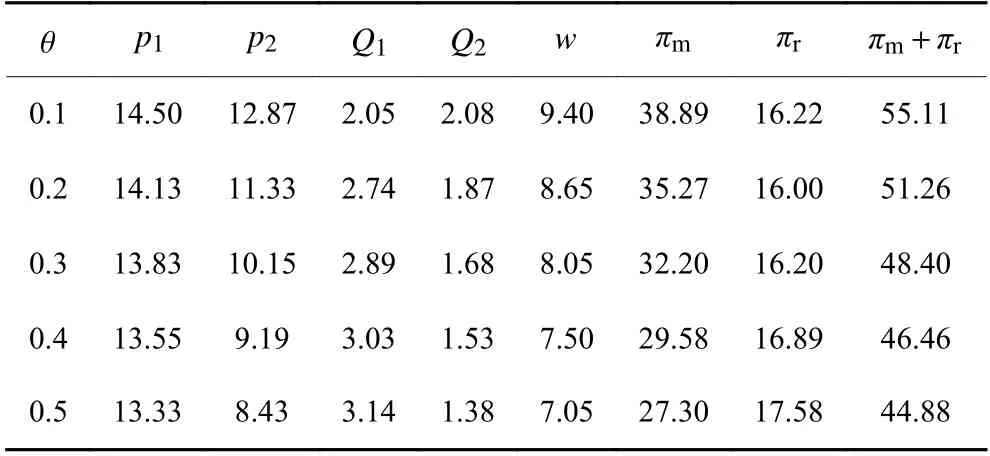
表4 不具回扣的主从对策鲁棒对应模型最优决策 (ρ =0.1)Table4 The optimal decisions of the robust counterpart without rebate (ρ =0.1)

表5 具有回扣的主从对策鲁棒对应模型最优决策 (ρ =0.1)Table5 The optimal decisions of the robust counterpartwith rebate (ρ =0.1)

3) 管理启示。

考虑如智能手机、潮流服饰等产品需求的不确定性以及时间和价格敏感性特征，根据上述数值分析结果，为具有两次定价订货机会的供应链运营提出如下管理启示。

(1) 对于需求具有时间和价格敏感性的产品，为了缓解产品吸引力的降低，零售商在第二阶段应实施降价销售策略。此外，制造商通过降低批发价格方式实施回扣激励机制，会进一步刺激零售商降价以增加需求。在这种情况下，制造商、零售商以及供应链总利润都将得到改进，从而有利于供应链的持续发展。

(2) 需求不确定性水平的增加会显著损害供应链及成员双方的利润，表明管理者在日常经营中应注重相关数据的收集与分析，提高需求预测精度以确保获得理想的利润。特别地，在需求不确定性增加时，制造商和零售商要保守应对，降低其批发价格和销售价格。

(3) 价格敏感增量越大，制造商和零售商越要降低批发价格和销售价格，以减缓需求量下滑，并且制造商要给予零售商更多的回扣以支持零售商的降价策略。此外，通过数值分析发现价格敏感增量的增加对制造商利润影响较大，这表明制造商可协助零售商实施一定的营销措施，维持产品在整个销售周期的吸引力。

5 结论

本文在不确定需求环境下，针对具有价格和时间敏感性需求的报童产品，建立了以制造商为主方，零售商为从方的具有两次定价订货机会的供应链鲁棒优化模型。根据制造商是否在第二阶段降低批发价格，将模型分为具有回扣的主从对策模型和不具回扣的主从对策模型。利用分段线性函数刻画需求的价格和时间敏感性特征；利用区间不确定集合描述需求的不确定性，并在此基础上分别获得两种主从对策模型的鲁棒对应模型。数值结果表明，在具有回扣的主从策略下，制造商、零售商及供应链总体利润均较高。需求不确定性的增加会显著降低供应链及成员利润绩效。当零售商第二阶段需求价格敏感性增加时，供应链双方会采取更为保守的定价和订货策略。未来，可设计相应的供应链协调机制，使得制造商和零售商在获得自身利润最大化的同时实现供应链协调，或在此模型基础上考虑多产品问题，并加入制造商生产提前期或零售商运输提前期的不确定性。