基于无穷范数空间距离的计数型函数响应优化方法研究

王贤鹏，何 桢

(天津大学 管理与经济学部，天津 300072)

在制造业质量管理实践中，很多重要过程和产品的质量特性由响应变量与协变量之间的函数关系表示。函数型质量特性分析优化在汽车制造、零件车削加工、木制品加工、金属注射成型等制造过程和产品中需求广泛。例如，汽车制造业中，汽车发动机不同转速对应的不同功率决定了汽车在起步、前行和刹车时的加速特点，该特性曲线受发动机制造材料厚度、线圈匝数、宽节比等因素的影响[1]；零件车削加工过程中，零件的特定形状可表示为曲率、宽度与长度的函数，该函数关系受进刀深度和切割速率的影响[2-3]；金属注射成型过程中，金属件的重量随高注射压力的变化有所不同，零件重量与高注射压力之间的函数关系受注射速度、紧固时间、紧固压力、高注射时间等因素的影响[4]。

在上述函数型质量特性例子中，功率值、形状参数值、重量等都是连续型变量，因此该类质量特性属于连续型函数响应。当响应变量类型不是连续型，而是计数型时，响应变量与协变量之间形成的函数关系即为计数型函数响应。计数型函数响应优化在工业制造业具有重要的应用。以手机液晶显示屏制造过程为例，驱动集成电路与液晶屏导电层之间需要通过混有金属球粒子的各向异性导电胶实现电路连接。在一定温度压力条件下，树脂胶固化使驱动集成电路与液晶屏导电层之间实现粘连，同时金属球粒子绝缘层爆破，粒子球上下表面分别与驱动集成电路和液晶屏导电层连接，实现二者的电路导通。驱动集成电路引脚可达上千，从左至右均匀排布，与液晶屏导电层端子对应区域一一连接。每个引脚区域内爆破的有效粒子数决定了该线路的电路导通电流大小，决定了液晶屏的像素显示效果。驱动集成电路不同位置对应的引脚区域内有效金属球粒子数量与位置变量之间构成计数型函数响应。该计数型函数响应受到温度、压力、压接时间等工艺参数的影响。通过优化有效粒子数与引脚位置变量的函数响应，可以改善液晶屏画面显示质量。计数型函数质量特性的优化对制造业质量改善具有重要应用价值，因此本文对该类响应优化方法进行研究。

1 文献综述

国内外学者已对连续型函数响应的试验设计和优化方法进行了较多研究。Govaerts等[5]提出采用基于多项式参数模型、按点函数回归等方法，对非线性质量特性曲线进行优化。Del等[6]从贝叶斯预测的角度，提出基于二阶段层级混合效应模型的函数响应优化方法。Goh[7]提出线性质量特性的因子筛选和优化方法。许静等[8]提出基于主成分分析的双响应曲面法和满意度函数相结合的函数响应优化方法。Pan等[9]基于混合效应模型提出响应协变量与试验因子选点的试验设计方法，并给出了用于搜索D-optimal设计的算法。

针对多元函数响应优化问题，Fogliatto[10]基于Hausdorff距离指标，结合满意度函数法，对函数响应与数值响应同时优化。Bakhtiarifar等[11]基于函数带深度和过程能力指数，提出多元函数响应的综合优化方法。

已有研究主要针对的是连续型函数响应的分析和优化方法，对计数型函数响应研究较少。本文以计数型函数响应为研究对象，基于无穷范数空间距离和满意度函数方法，提出包含计数型函数的多响应优化方法。通过仿真试验，说明本方法能够更精准地反映函数响应与目标函数之间的实际距离。最后，本方法应用于某液晶显示屏制造商的柔性电路板与玻璃基板压接工艺改进实例分析，结果令人满意。

2 方法构建

2.1 计数型响应与协变量模型构建

记计数型函数响应的协变量为t，第i次试验因变量为yi(t)。假定每次试验协变量t的观测值相同，且yi(t) 服从参数为µi的泊松分布，即

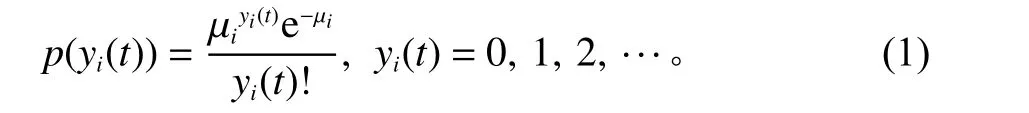
其中，p(yi(t))是yi(t)的概率质量函数；µi是位置参数；yi(t)! 表示yi(t)的阶乘，即yi(t)!=1×2×···×yi(t)；yi(t)的所有可能取值为非负整数。给定泊松分布参数µi，则可以估计计数型响应样本的均值为E(yi(t))=µi， 方差为Var(yi(t))=µi。

构建因变量yi(t) 与协变量t的广义线性模型。记联系函数为g(·)，采用对数函数作为联系函数，对位置参数µi进 行转换，并记转换后的值为ηi，即

构建ηi与协变量t之间的线性模型为

其中，T是对应于协变量t的模型矩阵。当模型中只包含协变量的一阶项时，有

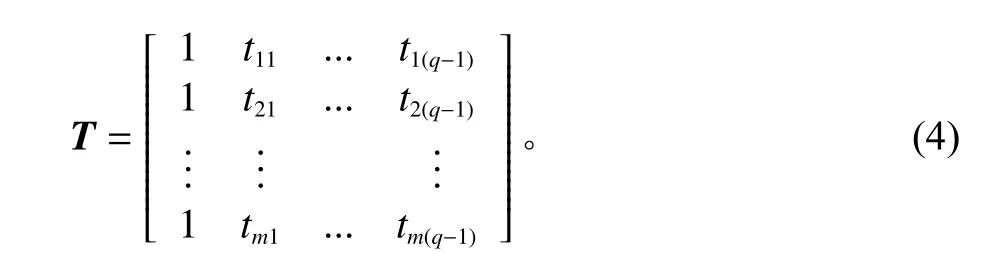
θi为q维参数列向量。

采用迭代再加权最小二乘算法，对模型参数进行极大似然估计，采用似然比检验方法，检验广义线性模型和回归系数的显著性[12]。进而通过式(2)和(3)估计函数响应的拟合值向量。

2.2 基于无穷范数空间距离指标的函数响应优化方法

参考Fogliatto等[10]基于观测值向量Hausdorff距离的函数优化方法，本文在向量的范数空间内衡量函数之间的距离，结合满意度函数法提出计数型响应优化方法。本方法主要特点如下。1) 考虑响应的函数特性，采用拟合值向量而非观测值向量进行优化。2) 在无穷范数空间内计算响应向量与目标函数向量的距离，作为计算满意度的基础。这样做的优势在于：(1) 能够更精准地反映函数向量之间的距离；(2) 通过使函数响应因变量中距离目标函数最远的点最近，保证所有函数点都令人满意。

记第i次试验所对应的计数型函数拟合值向量(yˆi1(ti1),···,yˆim(tim) ) 为yˆi。在正无穷范数空间中，向量yˆi与目标向量C之间的距离为[13]

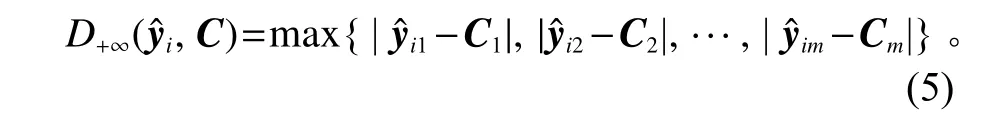
在负无穷范数空间内，向量yˆi与向量C之间的距离为

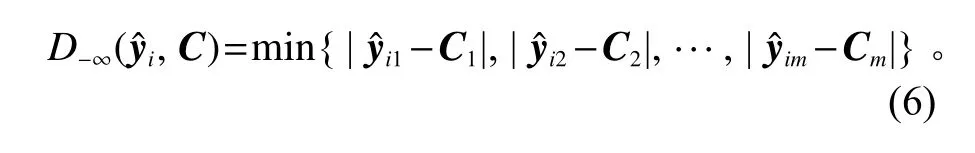
在工程实践中，优化目标通常分为望目、望大和望小3种情形。在望目情形下，优化目标是使函数响应接近某一目标函数，即应使估计的函数拟合值向量与目标函数向量的距离越小越好。在正无穷范数空间内，优化目标为

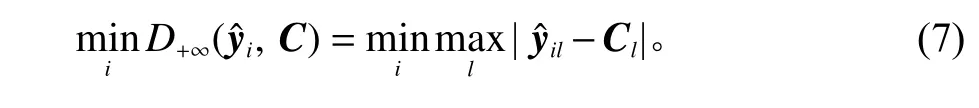
式(7)的解是使响应中距离目标函数对应点绝对距离最大的距离值最小，保证函数响应中的所有点均令人满意。

在望大情形下，优化目标是使函数响应在某一规格下限函数的上方，且越远离越好。记规格下限函数对应于协变量观测值的响应向量为L，在负无穷范数空间内，优化目标为

式(8)的解是使响应中距离规格下限函数对应点绝对距离最小的距离值最大，保证函数响应中的所有点均令人满意。

在望小情形下，优化目标是使函数响应在某一规格上限函数的下方，且越远离越好。记规格上限函数对应于协变量观测值的响应向量为U，则优化目标为

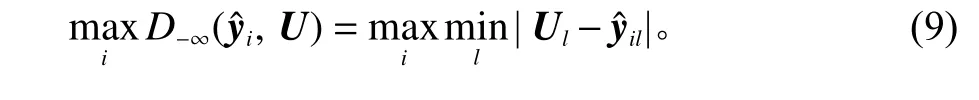
式(9)的解是使响应中距离规格上限函数对应点绝对距离最小的距离值最大，保证函数响应中的所有点均令人满意。

2.3 包含计数型函数响应的多响应优化方法

当试验中有R(R＞1)个需要关注的质量特性时，在优化中需要对各个响应的满意程度进行综合考量。考虑第r个响应为计数型函数响应，结合传统满意度函数方法[14-15]，基于无穷范数空间距离指标定义满意度水平。

对于望目情形，记函数响应拟合值向量与目标函数向量的最小距离为变量DLr，最大距离为变量DUr，采用线性满意度函数，则不同因子水平所对应的响应满意度为

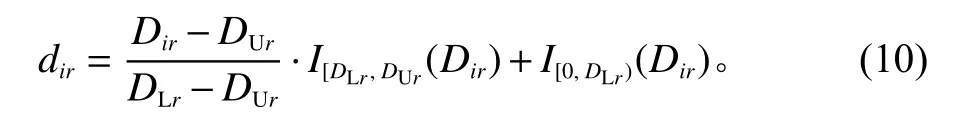
其中，I[a,b](Dir)为指示函数，且有

对于望大或望小情形，在负无穷范数空间内，函数响应拟合值向量与规格下限或规格上限函数的最小和最大距离分别为DLr和DUr。则不同因子水平所对应的响应满意度为

对于q个响应中的非函数型一般响应变量，采用传统满意度函数法对响应满意度进行评价。参照传统满意度函数优化方法，综合考虑多个响应的满意度，计算总体满意度值为

其中，wr为 第r个响应的权重。通过找到使D(di1,di2,···,diq)最大的因子水平组合，实现过程优化。

3 仿真试验

本节通过仿真试验对本文所提方法的优势进行分析，主要讨论：1) 与直接采用观测值向量作为响应相比，采用拟合值响应进行分析的优势；2) 比较Hausdorff距离、欧氏距离、无穷范数空间距离的可靠性。

采用广义线性模型 η=α+βt+ε (µ =exp(η)为泊松分布位置参数)，随机生成计数型函数响应并进行仿真试验。设定模型截距项为α=2，斜率为β=0.5，协变量t的取值为(0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0)，则函数响应拟合值向量真实值为(9, 12, 16, 20, 26,33, 43, 55)。假设随机误差ε服从均值为0，标准差为1的正态分布。随机生成10 000组观测值样本，并对每一个样本拟合广义线性模型，得到计数型拟合值向量。

设定目标函数为=1+0.5t，则目η标函数向量为(3, 4, 6, 7, 9, 12, 16, 20)。分别计算每一组随机样本的观测值和拟合值向量与目标函数向量之间的Hausdorff 距离、正无穷范数距离、负无穷范数距离以及欧氏距离指标。为评价不同方法的准确性和波动性，计算距离的样本均值和方差，结果见表1。

表1 拟合值和观测值向量与目标向量的不同距离指标值的均值和方差Table1 Mean and variance of different distances from the fitted and predicted vectors to the target vector

由表1可见，采用拟合值和观测值计算的所有距离与真实距离值都有一定偏差。相较于采用观测值进行计算，拟合值向量的偏差明显较小。从波动性大小来看，除了负无穷范数空间距离，采用观测值进行计算的标准差值明显大于拟合值向量距离指标的对应值。从该仿真试验结果可以看出，对于计数型函数响应，采用拟合值向量进行计算，明显减小了距离估计结果的偏差和波动性。总体而言，采用拟合值向量的Hausdorff距离和无穷范数空间距离进行计算分析，偏差和波动性更令人满意。

4 实例分析

某企业手机液晶显示屏模组关键过程为将驱动集成电路(integrated circuit，IC)和柔性电路板(flexible printed circuit，FPC)分别与玻璃基板通过各向异性导电胶压接。这两个过程分别称为Chip on Glass(COG)和FPC on Glass(FOG)工艺。在一定温度、压力和时间条件下，导电胶固化使驱动IC、FPC与玻璃基板实现粘连，同时导电胶内金属球绝缘层爆破，使驱动IC、FPC和玻璃基板导电层实现电路连接。图1为驱动IC和FPC与玻璃基板连接位置的示意图。图2显示了高位显微镜下驱动IC和FPC与玻璃端子压接区域的局部放大图。图中在条状区域内凸起的点为爆破的金属球粒子。对于驱动IC，条形压接区域从上到下区分电流流通的输入和输出端，因此，有效爆破粒子数与左右横向和上下纵向位置变量构成计数型函数响应。对于FPC，压接区域从左至右，不分输入和输出端，因此，有效爆破粒子数与横向位置变量构成计数型函数响应。

图1 驱动IC和FPC与玻璃基板连接位置示意图Figure1 The diagram of the bonding locations of the Drive IC and the FPC on the glass substrate

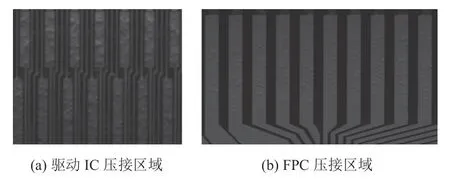
图2 驱动IC和FPC与玻璃基板压接区域的局部放大图Figure2 Partial enlarged detail of the bonding areas of the Drive IC and the FPC on the glass substrate

2019年5月～ 8月，产品不合格率呈明显增长趋势。经图像检测，发现不合格原因主要是由于驱动IC与玻璃基板之间有效粒子数减少。由图1可以看出，FPC和驱动IC连接位置较近，工艺工程师推断经过COG压接的驱动IC在FOG阶段可能会由于热传导或应力传导等影响使IC与玻璃基板导电层的连接状态发生变化。为解决该问题，需优化FOG工艺参数，改善驱动IC有效粒子数减少问题，同时保证FPC压接质量。

经讨论分析，确定影响因子为压接温度、压接时间、压力和风管吹风延时时间。采用24-1部分析因子试验方案，并在中心点位置增加5次试验。试验方案如表2所示。为减少重复测量所造成波动性的影响，每次试验采用3个试验件，利用自动光学检测设备获得试验件IC和FPC连接区域的例子爆破图像。

表2 因子试验设计方案Table2 The design plan of the factorial experiments

在FOG前后，分别测量记录各个试验件驱动IC左、中、右侧输入和输出端同一区域的有效粒子数。试验完成后，计算各个试验件驱动IC不同连接区域对应的有效粒子减少数量，结果见表3；各试验件FPC左、中、右侧选定区域的合格爆破粒子数量见表4。其中次序对应于试验的运行序。

表3 驱动IC左侧(L)、中段(C)、右侧(R)的输入(In)和输出(Out)端对应区域的粒子减少数量Table3 Reduced numbers of the particles in the left (L), center(C), and right (R) sides of the input (in) and output (out) parts of Drive ICs

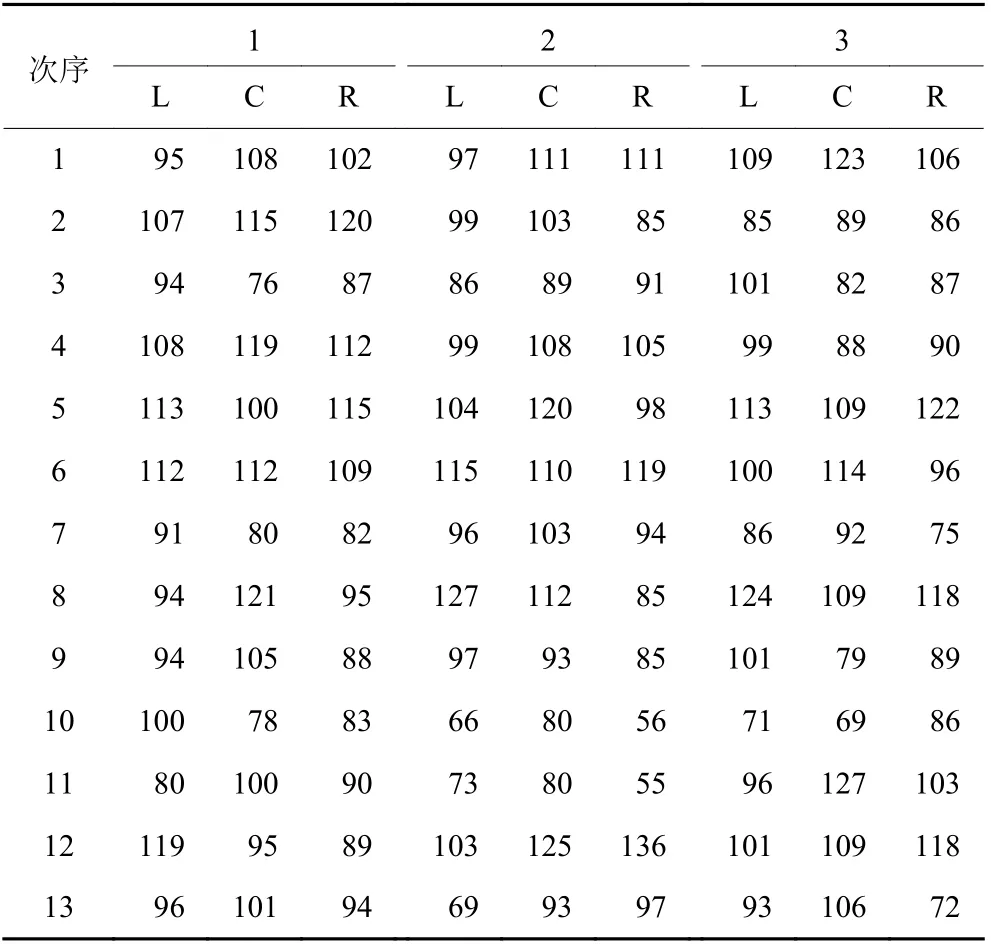
表4 FPC左侧(L)、中段(C)、右侧(R)区域的合格爆破粒子数Table4 Numbers of qualified broken particles at the left (L),center (C), and right (R) sides of FPCs

由于粒子减少数为离散计数型数据，且数值较小，故采用响应为泊松分布的广义线性模型拟合粒子减少数与位置变量的关系。记左、中、右侧位置变量值为−1、0、1，记输入和输出位置变量值为0、1，对每个试验件拟合回归模型。考虑在左中右位置方向上可能存在弯曲性，回归模型形式为η=α+ω1x1+ω2+ω3x2。其中，x1为左中右横向位置变量；x2为输入输出端纵向位置变量；α为截距项；ω1和ω2分别为x1的一次和二次项系数；ω3为x2的一次项系数。回归系数估计值见表5。

表5 粒子减少数量与位置变量的广义线性回归模型参数估计值Table5 Parameter estimates of the generalized linear regression model for the reduced particle numbers and the location variable

经检验，所有模型均是显著的。同时，在90%的置信水平下，几乎所有模型截距项均显著，各个试验响应的位置变量的线性和弯曲性参数的显著性不完全相同。进一步计算拟合值向量如表6所示，其中L、C、R分别为左、中、右；In和Out代表输入和输出端。FOG之后不同试件的FPC在左中右位置上的有效粒子数如表7所示。

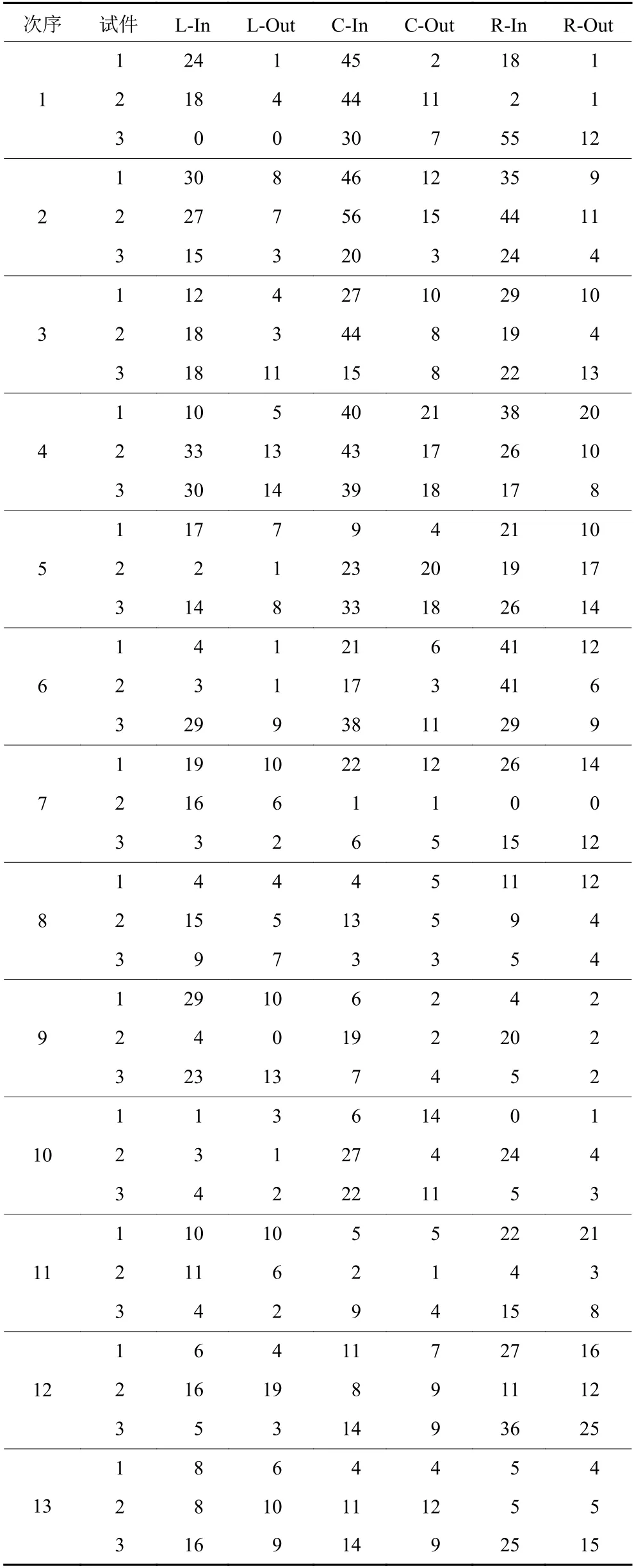
表6 驱动IC压接区域粒子减少数的广义线性模型拟合值向量Table6 Fitted vectors for the generalized linear model for the reduced number of particles in the bonding areas of Drive ICs

对于驱动IC的粒子减少数，优化方向为望目，最理想的目标函数为所有位置上的粒子减少数均为0，即目标函数向量为(0, 0, 0, 0, 0, 0)。对各次试验驱动IC的拟合值向量的3次重复测量值取平均，并计算平均拟合值向量与目标向量的正无穷范数距离，结果见表7。对于FPC的有效粒子数，优化方向为望大。分别计算这两个响应的满意度，结果如表8所示。

表7 FPC在左中右位置上的有效粒子数Table7 Qualified particle numbers at the left, center,and right sides of FPCs

根据表8，综合满意最高的为第8次试验。在表2的试验设计方案中找到对应的因子水平组合为温度180 ℃，压接时间为10 s，压力为110 N，吹风延时为6 s。按照该结果设定工艺参数，产线11、12月份由有效粒子数减少造成的产品不合格率显著下降。

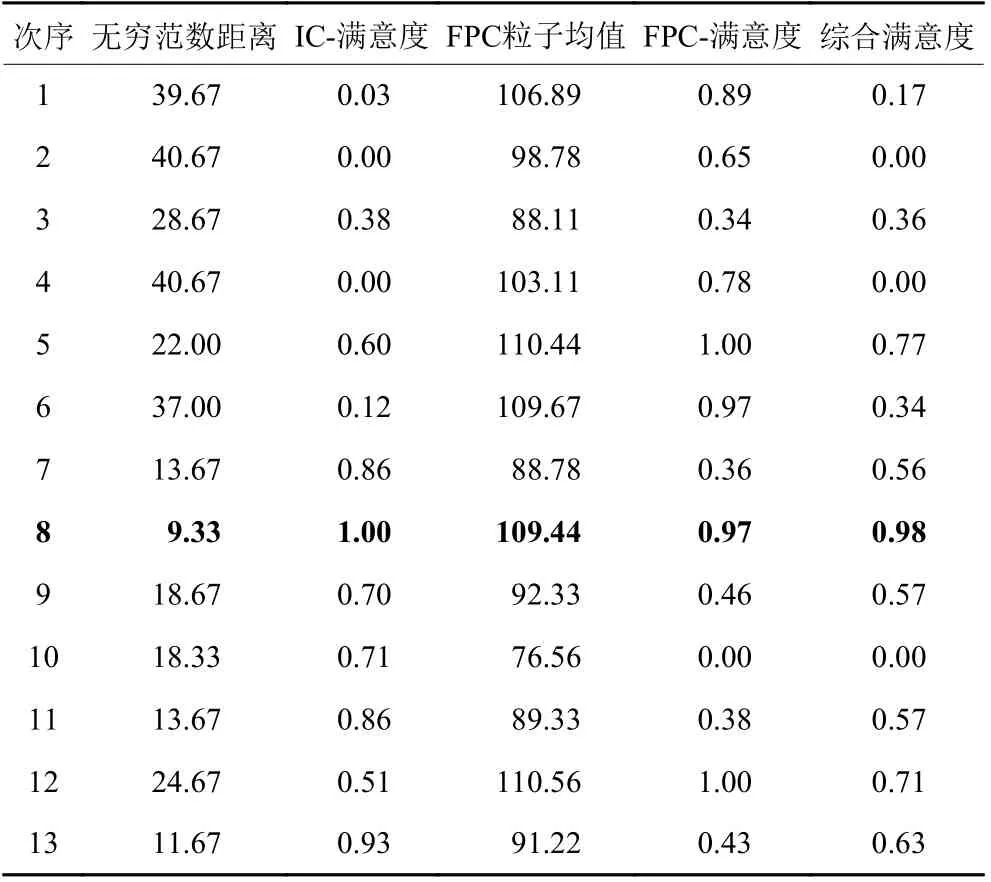
表8 驱动IC有效粒子减少数与位置关系的函数响应和FPC平均有效粒子数响应的综合满意度Table8 The overall desirability for the functional response of reduced particle numbers and the location variable for Drive ICs and the mean qualified particle numbers for FPCs

5 结论

本文基于拟合值向量的无穷范数空间距离指标，结合满意度函数法，提出一元和多元计数型函数响应优化方法。仿真试验结果表明，与Fogliatto等采用的函数观测值向量的Hausdorff距离指标相比，本文提出的拟合值向量无穷范数空间距离指标更精准地反映函数响应向量之间的真实值。本文提出的优化方法应用于某公司液晶显示屏模组FOG工艺参数改进，成功改善驱动IC有效粒子数减少问题，同时保证了FPC压接质量，有效降低了产品不合格率。