次生舆情影响下的网络舆情传播研究

江长斌，李汾萦，张瑶源，王周阳，任天宇

(1.武汉理工大学 管理学院，湖北 武汉 430070；2.武汉大学 经济与管理学院，湖北 武汉 430072)

近年来，各类突发事件通过网络迅速传播，集聚了公众的注意力，也引发了舆论热议，如新冠肺炎疫情、8·12天津港爆炸、重庆公交车坠江事件和3·21响水化工厂爆炸等。突发公共事件不仅严重威胁公众的生命安全，造成巨大的经济损失，与之相关的舆情事件通过网络空间迅速传播，引发社会恐慌，扰乱社会秩序。在网络舆情的传播过程中，由于原生舆情的处理不当等原因，还会产生一系列的次生议题，诱发次生舆情，进一步激化社会矛盾。次生舆情一般与原生舆情息息相关，由其直接诱发，但是更加复杂，且一个舆情事件可能催生多起次生舆情，给网络舆情的监管带来巨大压力。如在新冠肺炎疫情期间，“红十字会物资调配”和“物资拦截”等多起次生舆情事件的爆发都促使舆情治理环境进一步复杂化。

舆情治理能力是政府治理能力的重要组成部分。在网络舆情传播过程中，次生舆情的产生往往会改变舆情事件的演化强度或趋势，为舆情管理机构的舆情管控工作带来困难。研究次生舆情对原生舆情传播过程的影响对提升舆情治理能力有重要作用，但目前鲜有研究者关注次生舆情与原生舆情的交织传播过程。因此，笔者将全面分析不同情况下次生舆情对舆情传播过程的影响，探索政府干预行为在舆情传播过程中的实际效果，帮助舆情管理机构准确把握次生舆情影响下的网络舆情传播规律，提升舆情治理能力。

1 文献综述

公众受事件刺激后在网络上公开表达自己对事件的认知、态度、情绪和意见，他们的观点逐渐统一形成网络舆情并在社交网络空间传播扩散[1]。FRAHM等[2]提出了识别社交网络上网络舆情形成的Ising-PageRank模型，实验发现即使意见领袖占比很小，其仍能显著影响舆情观点的形成。NUORTIMO等[3]指出社会媒体对舆情的影响正逐渐增强，放大了网络舆情的社会影响。方付建[4]认为网络舆情诱发的种种后果会给各类群体造成不可忽略的影响，一旦舆情事件处理不当，这种影响的负面效应将给社会的正常秩序带来巨大的挑战。周义棋等[5]认为网络舆情分析有助于掌握民众情感动态，在热点事件中，官方微博积极引导有助于民众舆论正向发展。

目前学术界对次生舆情的定义尚未统一，与原生舆情概念相对应，次生舆情大体上是指在原生舆情基础上由某一因素触发生成的新舆情信息，与原生舆情交织传播。赵静娴[6]认为广义的次生舆情是分正负的，狭义的次生舆情都是负面的。周庆安等[7]认为当前政府部门或企业组织经常会面临原生舆情处理不当而产生的次生舆情危机，这些次生危机往往具有自身独特性，处理不当将会给组织声誉带来冲击。罗萍[8]分析了次生舆情的3种效应及其可能产生的后果。刘勇等[9]指出重大公共危机中次生舆情的生成已成为常态，其中多数为负面舆情。陈婷等[10]针对网络舆情的衍生效应，构建了基于时序信息的话题演化模型从而对衍生舆情实时追踪。刘文强[11]基于系统动力学模型和模糊三角数提出了移动社交网络次生舆情的预警方法，将舆情预警程度划分为5个等级。安璐等[12]基于热点主题提出了突发事件次生衍生事件的判定规则，实现了从舆情事件传播过程中的多个舆论焦点里探测次生衍生事件。郑智斌等[13]指出次生舆情可能强化或改变舆情演化方向，具有后发性、围合性、关联性、偶然性、敏感性和话题性等特征。郑万军[14]从3方面提出了减少突发危机事件中网络谣言等次生危害的路径。

SUDBURY[15]首次将传染病SIR模型用于研究谣言传播，为舆情传播研究提供了新的思路。之后许多学者通过改进传染病模型对舆情的传播规律和影响因素进行了研究，相较于其他模型，传染病模型不仅能够很好地展现舆情传播的规律，还能够有效帮助分析各种舆情控制策略的效果[16]。JIANG等[17]基于传染病模型构建了SPNR模型，验证了政府公布事件真相的时间对谣言传播有重要影响。林晓静等[18]考虑新网民的加入，提出了具有饱和接触率的SEIR模型，研究了动态社交网络中的舆情传播扩散过程。ZHANG等[19]将传播节点分成了支持、中立和反对，构建MI-SEIR模型分析了媒体与人际关系对舆情传播的影响。成全等[20]在传统SEIR模型中加入用户主题兴趣作为舆情传播演化的影响因素，通过仿真实验发现传播用户数量、类别和舆情参与用户的主题兴趣度、主题关注焦点有显著关系。陈莫凡等[21]结合传染病模型和博弈的优势，构建了基于SEIQR的演化博弈模型，分析了专家、政府和网媒等因素对社交网络上舆情传播的影响。

总体而言，目前针对次生舆情对原生舆情传播过程影响的研究尚有不足，故笔者考虑两种舆情信息同时存在于社交网络，探讨次生舆情影响下的舆情传播过程和政府干预行为的作用，并提出相关治理建议。

2 模型构建

在用于网络舆情传播研究的多种传染病模型中，SEIR模型通过节点的易感、潜伏、感染、免疫4种状态较全面的反应了网络舆情的传播特性。以微博社交网络为例，舆情事件在微博上发酵之后，网友可以选择点赞、评论和转发等多种参与方式，其中只有转发行为可以直接扩散舆情信息。第一时间选择点赞和评论的网友可能在观望一段时间之后转发信息，也可能因为对舆情事件不感兴趣而不转发。可以发现，在这个过程中存在4种状态的网友：①还没有接触到舆情信息的网友，②选择点赞和评论的网友，③选择转发舆情信息的网友，④对舆情事件失去兴趣的网友。这4种状态与传染病SEIR模型中网络节点的4种状态大致相似，因此可以选择以SEIR模型为基础来构建舆情传播模型。

2.1 经典SEIR模型

SEIR模型将整个网络上的个体分为易感染者、潜伏者、感染者和免疫者4类。在该模型中，易感染状态节点在接触到感染节点之后不会直接成为感染者，而是先进入潜伏状态，概率为α，潜伏者不会直接感染他人。部分免疫力较强的人会在自身免疫系统的作用下恢复健康，成为免疫者，概率为γ；其他人会逐渐成为感染者，在网络系统中传播疫情，概率为β。随着时间的推移，感染者或死亡，或在药物的治疗下康复成为免疫者R，移除传染系统的概率为λ。SEIR模型的状态转移图如图1所示，模型的微分方程表达式如式(1)所示,其中S(t)+E(t)+I(t)+R(t)=1。

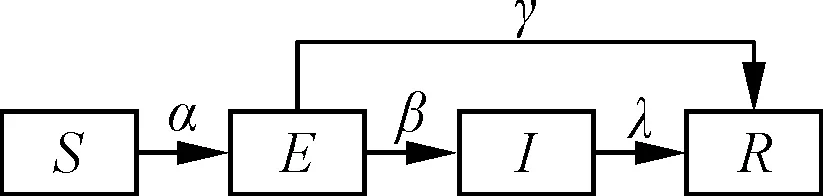
图1 SEIR模型

(1)

2.2 考虑次生舆情影响的SEIR模型

2.2.1 模型基本假设

假设1模型所构建网络为静态网络，社交网络中的网民数量在网络形成后不变，单位时间内同一传播过程中网络节点间的传播概率相等。

假设2在现实生活中，次生舆情在传播过程中大多会携带原生舆情信息，故网友在接触到次生舆情信息时都会对原生舆情事件有所了解。因此假设所有接触次生舆情信息的网友都知道原生舆情事件，传播次生舆情即同时传播两则舆情信息。

2.2.2 模型构建

目前，网络舆情事件中次生舆情的爆发已经成为常态，而传统的SEIR模型只考虑了一种感染源，对于次生舆情影响下的舆情传播过程具有局限性。因此，结合现实情况，对微博社交网络环境下舆情信息传播过程进行分析，在经典SEIR模型中加入次生舆情传播相关的节点状态，建立考虑次生舆情影响的舆情传播模型。根据网民对待舆情信息的态度，笔者将网络环境下的所有网络节点分为7种状态：未知节点(S)、原生舆情潜伏节点(E1)、次生舆情潜伏节点(E2)，原生舆情传播节点(I1)，次生舆情传播节点(I2)，原生舆情免疫节点(R1)和次生舆情免疫节点(R2)。原生舆情信息与次生舆情信息在社交网络上交织传播的过程如图2所示，该舆情传播模型的微分方程表达式如式(2)所示。

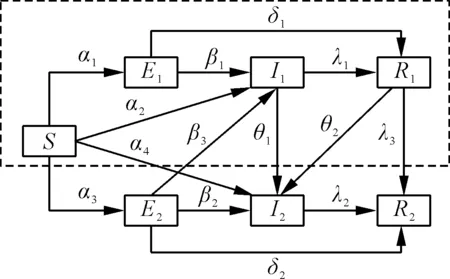
图2 舆情传播模型

(2)

未知节点S在接触到原生舆情信息后，部分较为理智的网友不会直接转发传播舆情信息，成为原生舆情潜伏者节点E1，概率为α1；但部分容易轻信的网友选择直接转发舆情信息，成为原生舆情传播节点I1，概率为α2。未知节点S在接触次生舆情信息后，网友同时了解原生舆情信息和次生舆情信息，较为理智的网友不会直接转发，成为次生舆情潜伏节点E2，概率为α3；虽然网友可以选择只转发次生舆情中包含的原生舆情信息或直接转发次生舆情信息，但考虑到在不确定信息真伪的环境下直接转发舆情信息的网友缺乏应有的理智，故认为其不会只转发原生舆情成为I1，只可能成为次生舆情传播节点I2，概率为α4。

E1节点在下一时间点进行判断，部分对舆情事件较为关心的网友会转发舆情信息，成为I1状态节点，概率为β1；其他网友在对舆情事件进行分析判断后选择不传播，成为原生舆情免疫者R1，概率为δ1。E2节点中同样存在部分网友在分析舆情信息后决定不传播，成为次生舆情免疫节点R2，概率为δ2；部分网友对次生舆情事件感兴趣、愿意关注事件发展，会转发次生舆情信息，成为I2状态节点，概率为β2；但是次生舆情信息一般为网友的揣测甚至谣言，不存在较充足的证据，故对舆情事件感兴趣且比较理智的网友可能选择暂时避开次生舆情信息而只转发原生舆情信息，成为I1状态节点，概率为β3。

I1状态节点表示当前正处于对舆情事件较为关注的状态，如果其接触到次生舆情信息则可能转发次生舆情，成为I2状态节点，概率为θ1；部分了解事件真相或较为理智的网友会选择暂时不传播，成为R1状态节点，概率为λ1；如果没有接触次生舆情则只会随着时间的推移成为R1状态节点。I2状态节点随着时间的推移会逐渐失去对舆情事件的兴趣成为R2状态节点，概率为λ2。

R1状态节点之前只了解原生舆情信息，当其接触到次生舆情信息时，次生舆情可能会重新激起网友对舆情事件的关注，转发次生舆情信息，成为I2状态节点，概率为θ2；但同样次生舆情的刺激可能不起效果，其忽略次生舆情信息成为R2状态节点，概率为λ3。R2状态为整个舆情传播过程的最终状态，任何节点进入到该状态后不再变化。

3 模型仿真

基于C++编程语言实现舆情在社交网络上的传播过程仿真，获得仿真数据之后使用Matlab进行图形绘制。仿真社交网络在有向无标度网络的基础上，构建了总结点数为5 000的网络。仿真初始，随机选择0.1%的节点令其成为I1状态，表示原生舆情信息进入社交网络。设置基础参数组α1=α3=0.8，α2=α4=0.2，β1=0.8，β2=0.5，β3=0.3，δ1=δ2=0.2，θ=0.8，θ2=0.5，λ1=0.2，λ2=0.8，λ3=0.5，社交网络节点nc=2。为提高实验的准确性，进行100次模拟仿真对模型进行验证，并取算术平均值。

在仿真实验过程中，由于次生舆情具备后发性的特点，故不能在仿真实验初始阶段设置初始的I2节点，而直接设定I2节点出现的时间步在程序设计上又存在一定难度。因此，考虑到初始仿真条件中不存在E1节点，设置当E1数量达到一定值时，随机选择nc个节点成为I2状态，表示次生舆情爆发，进入舆论场影响原生舆情事件的传播。通过调节I2状态节点出现的条件，改变次生舆情出现的时间点，完成次生舆情在不同时间步出现对原生舆情传播影响的对比实验。

3.1 次生舆情影响下的舆情传播仿真

3.1.1 次生舆情对舆情传播的影响

舆情事件发生后会快速吸引广大网友的关注，在聚光灯下事件真相的隐瞒或网友的猜测都有可能催生次生舆情，这些次生舆情会进一步推动舆情传播扩散，为舆情治理带来新的挑战。为了对比研究次生舆情的爆发对舆情事件传播过程的影响，设置无次生舆情和有次生舆情爆发的对照实验，实验结果分别如图3和图4所示。对比图3和图4可知，舆情爆发初期各状态节点曲线变化基本一致，但在t=3时间步之后，存在次生舆情的条件下，未知节点S数量下降得更快，而潜伏者E和传播者I的数量也快速增长，舆情峰值显著增大；在t=5时间步之后，无次生舆情影响条件下舆情免疫者R数量进入快速增长阶段，越来越多的节点对舆情失去兴趣。由于次生舆情具有后发性，在舆情爆发初期，两种条件下都是原生舆情事件在影响舆论走向，因此发展趋势相似。随后由于处置不当等原因，次生舆情爆发进入社交网络，推动舆情到达更大的峰值，舆情持续时间更长。

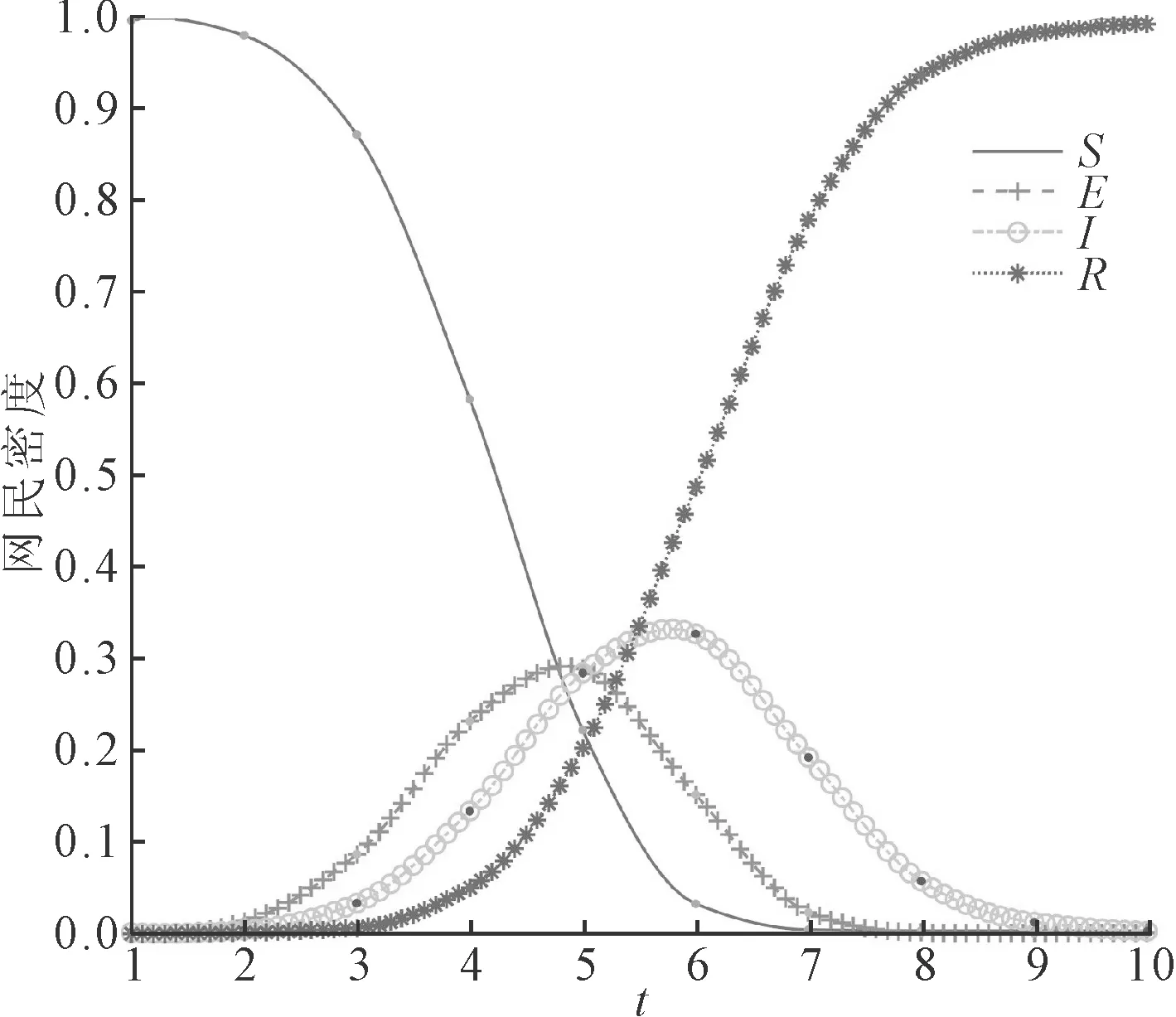
图3 无次生舆情影响下的舆情传播过程

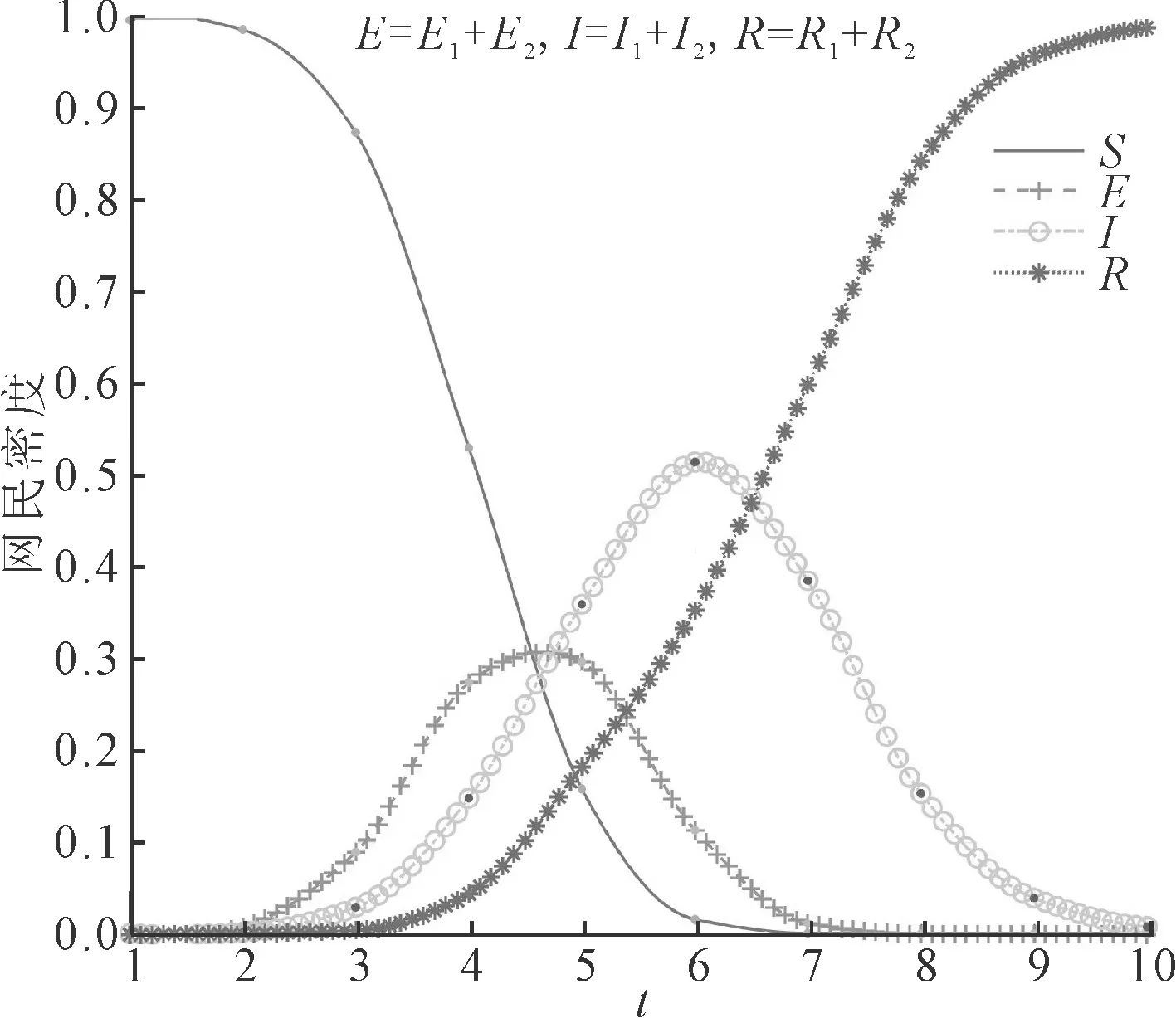
图4 次生舆情影响下的舆情传播过程

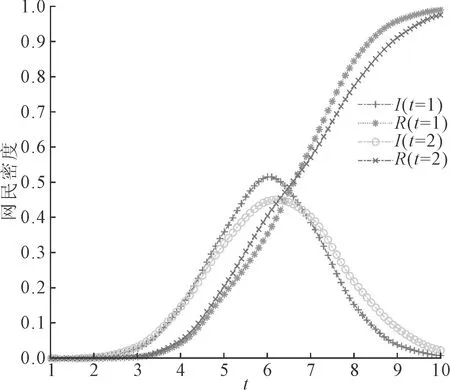
图5 不同时间产生I2节点条件下的舆情传播过程

(1)次生舆情出现时间节点对舆情传播的影响。原生舆情事件在传播演化过程中的所有时间节点都有可能诱发次生舆情，舆情初期诱发的次生舆情可能会伴随着原生舆情一起推动舆情扩散，吸引更高的关注度，舆情后期诱发的次生舆情可能会重新吸引网友对舆情事件的关注，致使舆情反复。为了对比次生舆情出现时间对舆情传播过程的影响，将仿真过程中的I2状态节点产生机制由E1>0更改为R1>5，根据舆情演化规则，在舆情传播一个时间步之后，只有初始状态下的5个I1节点可能成为R1状态，因此更换演化机制将使得I2节点在舆情演化2个时间步之后产生，此时的舆情传播过程如图5所示。由图5可知，与t=1条件下的舆情传播过程相比，在t=2时刻出现次生舆情信息条件下，舆情的峰值更小，但舆情峰值到达的时间相差较小，随着时间的推移，次生舆情爆发较晚的情况下舆情关注度反而较高。这是由于在次生舆情爆发较早的情况下，虽然原生舆情和次生舆情交织传播致使舆情达到更大峰值，造成巨大的影响，但是在舆情发酵较长时间之后爆发次生舆情会导致舆情事件又一次呈现在广大网友面前，部分已经遗忘事件的网友再一次传播舆情信息，整体表现为舆情事件在网络上获得较长时间的关注，消退更加缓慢。在现实生活中，存在部分在原生舆情消退期爆发的次生舆情，这些舆情致使网民沉寂的情绪再一次爆发，推动舆情到达二次高潮。因此，在舆情事件处理过程中，要顾及全面，解决所有可能存在的隐患，避免在舆情后期爆发次生舆情，致使舆情事件反复，造成社会秩序的长期混乱。

(2)次生舆情数量对舆情传播的影响。在现实生活中，一个原生舆情事件在发酵过程中可能会出现多个次生舆情，这些次生舆情共同影响着原生舆情事件的传播。为探究次生舆情数量对舆情传播过程的影响，改变次生舆情初始节点数量nc进行对比实验。由于不同次生舆情事件具备类似的特点，并且在传播过程中都围绕原生舆情进行扩散，故在实验中将不同次生舆情事件传播节点都归类于I2，通过设置不同数量的初始I2节点表示原生事件诱发次生舆情事件数量的不同。不同次生舆情数量下的舆情传播过程如图6所示，可知当次生舆情数量逐渐增加时，舆情峰值也随之增加；当次生舆情数量从1增加到2时，舆情峰值的增长更加明显；但随着次生舆情数量的进一步增长，即从2增加到3时，舆情峰值并未出现显著增长。这种情况在实际舆情传播过程的体现则是次生舆情数量的增长会使得舆情事件消息覆盖面更广，推动舆情峰值上升，但是当次生舆情数量达到一定值时，舆情信息已经以最快的速度覆盖了社交网络的绝大部分节点，这时次生舆情数量的持续增长难以促使舆情峰值继续上升。

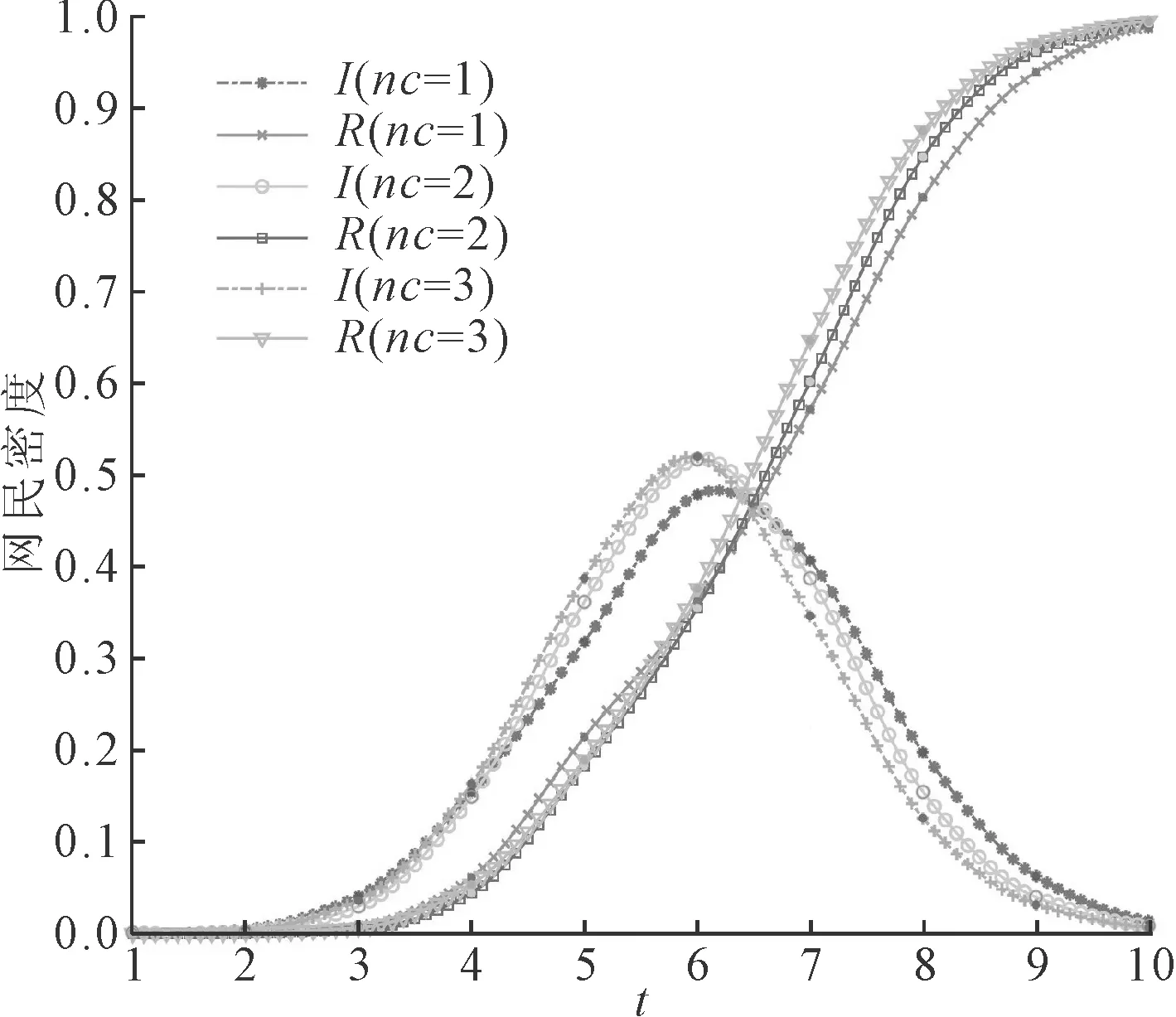
图6 不同次生舆情数量下的舆情传播过程

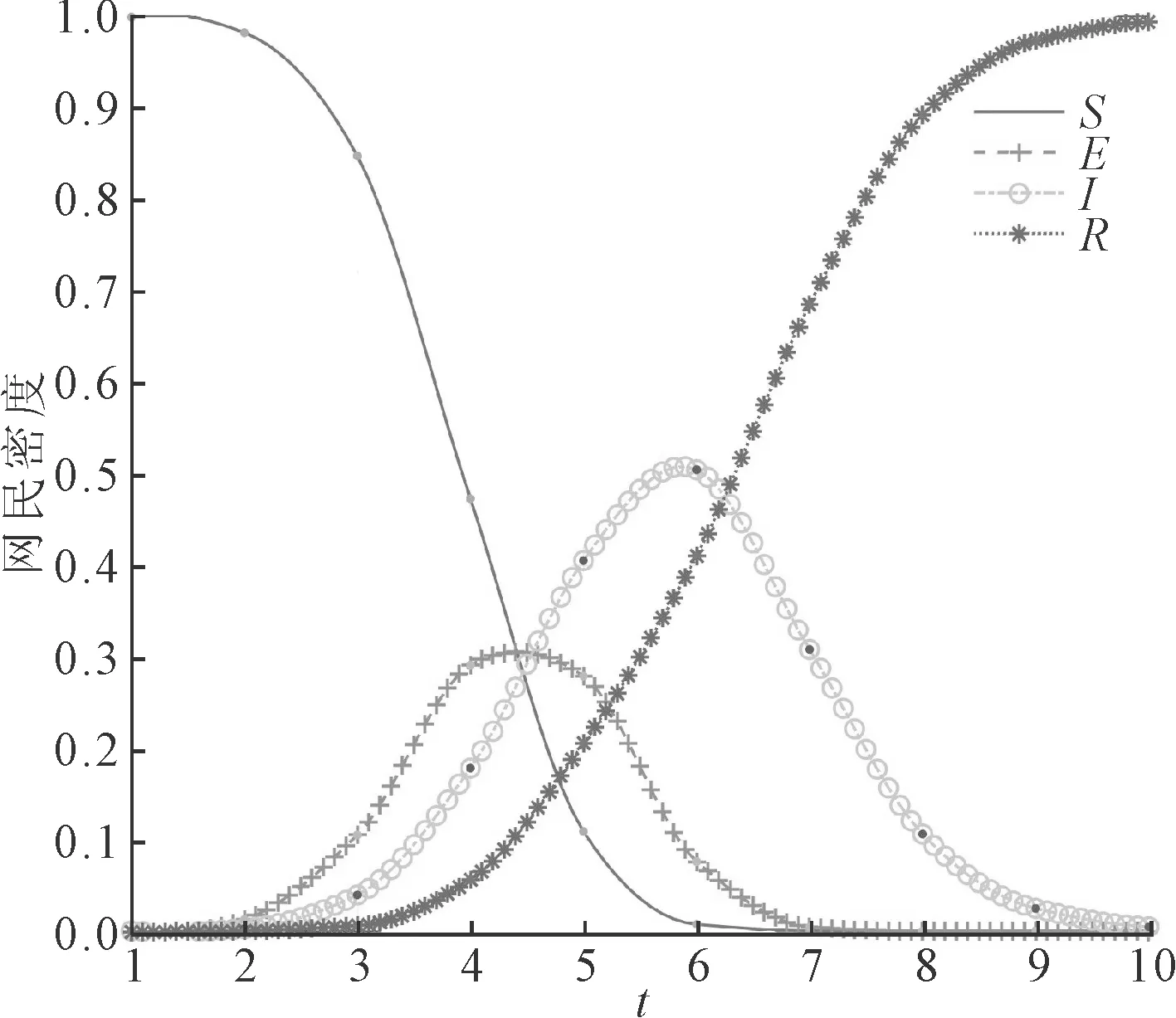
图7 α3=0.8、α4=0.3时的舆情传播过程

3.1.2 转发传播率对舆情传播的影响

(1)直接转发率对舆情传播的影响。在舆情信息进入社交网络时，如果大量网友在接触舆情的第一时间转发，极易将舆情事件推上热搜，在更短的时间内达到更大的舆情高峰。为了分析网友在接触舆情时直接转发舆情信息的概率对舆情传播过程的影响，调节参数α3和α4进行对比实验，得到α3=0.8、α4=0.3时的舆情传播过程，如图7所示。对比图7和图4可知，在更多的网友接触次生舆情并直接传播舆情的条件下，舆情传播者数量快速增长，在更短的时间达到高峰，同时由于网络中传播者数量的激增，导致舆情信息迅速扩散，整个网络中的未知者数量快速降低，潜伏者数量也提前达到峰值，但是舆情直接传播率的增长并没有使得舆情的峰值更大。这是因为现实中的网络足够庞大，任何舆情事件在微博上发酵，都难以实现遍及所有的微博用户，舆情传播者数量可以持续增长；而实验中网络节点数量有限，节点状态从未知者变成传播者之后会逐渐成为舆情免疫者，不再传播舆情，当未知者数量逐渐降低甚至不再有未知者时，潜伏者和传播者就失去了状态转移的来源，没有更多节点进入舆情传播者状态推动舆情达到更高峰值。

(2)次生舆情传播率对舆情传播的影响。在舆情传播过程中，公众的揣测、报复性抹黑和媒体的刻意诱导都是次生舆情爆发的重要原因，当广大网友面对这些未经证实的负面消息时，虽然部分网友或是由于从众心理，或是对涉事主体存在偏见，亦或是缺乏应有的理智而传播次生舆情，但是依旧有部分网友会对次生舆情信息提出质疑，即使对舆情事件比较关注，也会选择只转发次生舆情中包含的原生舆情信息。为研究网友在接触次生舆情后转发次生舆情的概率对舆情传播过程的影响，调节参数β2和β3进行对比实验，β2=0.4、β3=0.4得到时的舆情传播过程，如图8所示。对比图8和图4可知，两种条件下的舆情传播过程基本相似，但当网友接触次生舆情信息后选择传播次生舆情信息的概率的增大时，更多的网友会在接触到次生舆情信息后直接转发，推动舆情快速发展，达到更大的峰值。因此，在舆情发酵过程中，舆情管理部门需要时刻关注舆论的走向，当次生舆情出现时，要第一时间做出针对性的解释，并呼吁广大媒体帮助宣传事情真相，减少次生舆情信息的传播。同时可以通过宣传科普等方式增强网友的信息甄别能力，在次生舆情出现时保持理性，降低次生舆情传播概率。

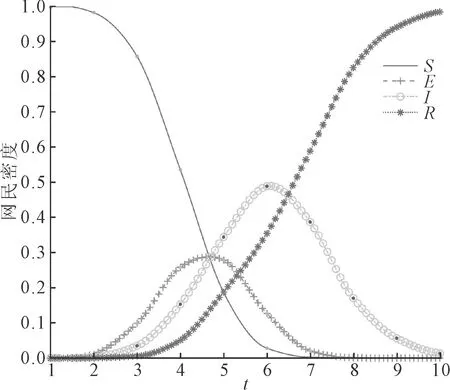
图8 β2=0.4、β3=0.4时的舆情传播过程

3.2 政府干预下的舆情传播过程仿真

3.2.1 干预原生舆情行为的作用

在现实情况中，政府的干预行为会降低网友对事件的关注度，减少网友在微博社交平台上转发或发布舆情相关博文的可能性，加速网络舆情的消退，这在仿真实验中直接表现为政府干预行为会改变舆情传播过程中网络节点在各个状态之间的转化概率[22]。

(1)有无干预原生舆情行为对比实验。在网络舆情爆发后，政府可以随时在舆情传播过程中采取应对措施，如召开新闻发布会公布事件信息，解答公众疑问，满足其信息需求，从而抑制网络舆情传播。虽然原生舆情干预行为没有直接影响到次生舆情的传播，但原生舆情因政府干预在社交网络上的扩散受到抑制时，次生舆情的关注度也会随之降低。因此，次生舆情在传播过程中会受到原生舆情干预行为的影响，在实验中体现为受到原生舆情干预行为时，α2、α4、β1、β2、β3、θ1、θ2等参数减小，α1、α3、δ1、δ2、λ1、λ2、λ3等参数增大。由于次生舆情的关注点与原生舆情存在一定差异，且原生舆情的干预策略对次生舆情具有影响但相对较小，因此假设政府对网络舆情进行控制引导时，原生舆情受到的干预系数为0.1，而次生舆情受到的干预系数为0.05。即α1=0.9，α2=0.1，α3=0.85，α4=0.15，β1=0.7，β2=0.475，β3=0.275，δ1=0.3，δ2=0.25，θ1=0.75，θ2=0.45，λ1=0.25，λ2=0.85，λ3=0.55，nc=2。原生舆情干预行为下的舆情传播过程如图9所示。对比图9和图4可知，政府在舆情事件爆发后采取紧急措施能够有效抑制舆情的传播。舆情峰值不但会推迟到来，给舆情管理部门更多的反应时间，而且最终的舆情峰值会显著减小。此外，政府干预原生舆情的环境下，舆情散播速度也更慢，潜伏者数量的增长速度和未知者数量的下降速度都有一定的减缓。因此在网络舆情爆发之后，舆情管理部门可以在第一时间召开新闻发布会，公布事件详细信息，满足公众的信息需求，以抑制网络舆情传播。

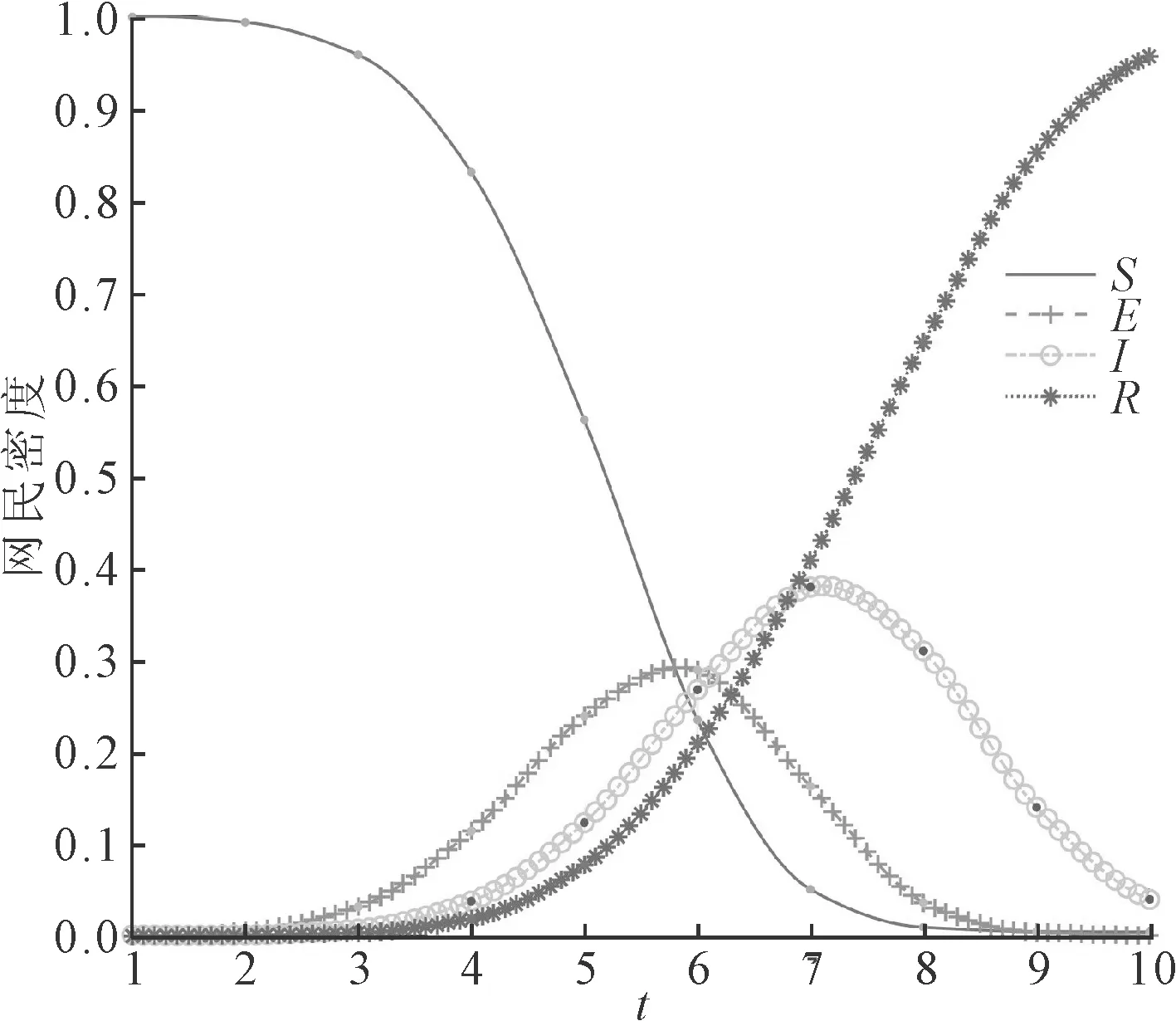
图9 原生舆情干预行为下的舆情传播过程

(2)不同时间点干预原生舆情对比实验。政府针对原生舆情的干预行为能够有效抑制舆情传播，但当舆情发酵到一定阶段后，政府干预行为的作用到底如何尚未可知。一方面，在现实情况下，政府并不会按照固定的时间实施干预，更多是根据舆情发展形势来判断是否需要采取措施，而不同时间节点的舆情传播者数量是舆情事件发展态势的主要判断指标；另一方面，在仿真实验中难以实现在固定舆情传播时间后人为调整舆情传播参数。为了对比不同时间政府干预原生舆情行为的效用，在观察原生舆情传播节点I1数量变化规律后设置如下机制：舆情传播初期，各传播参数采用基础参数组的数值；在原生舆情传播一段时间后，原生舆情传播节点数量I1>500时，政府干预启动，各参数发生变化，此时的舆情传播过程如图10所示。对比图4、图9和图10可知，在政府对原生舆情及时做出干预行为的条件下，可以有效抑制舆情传播速度，未知者的数量下降更加缓慢，舆情峰值更低。而如果政府在舆情信息传播一段时间之后再采取干预行为，虽然也能够在一定程度上抑制舆情传播，但效果相对较差。

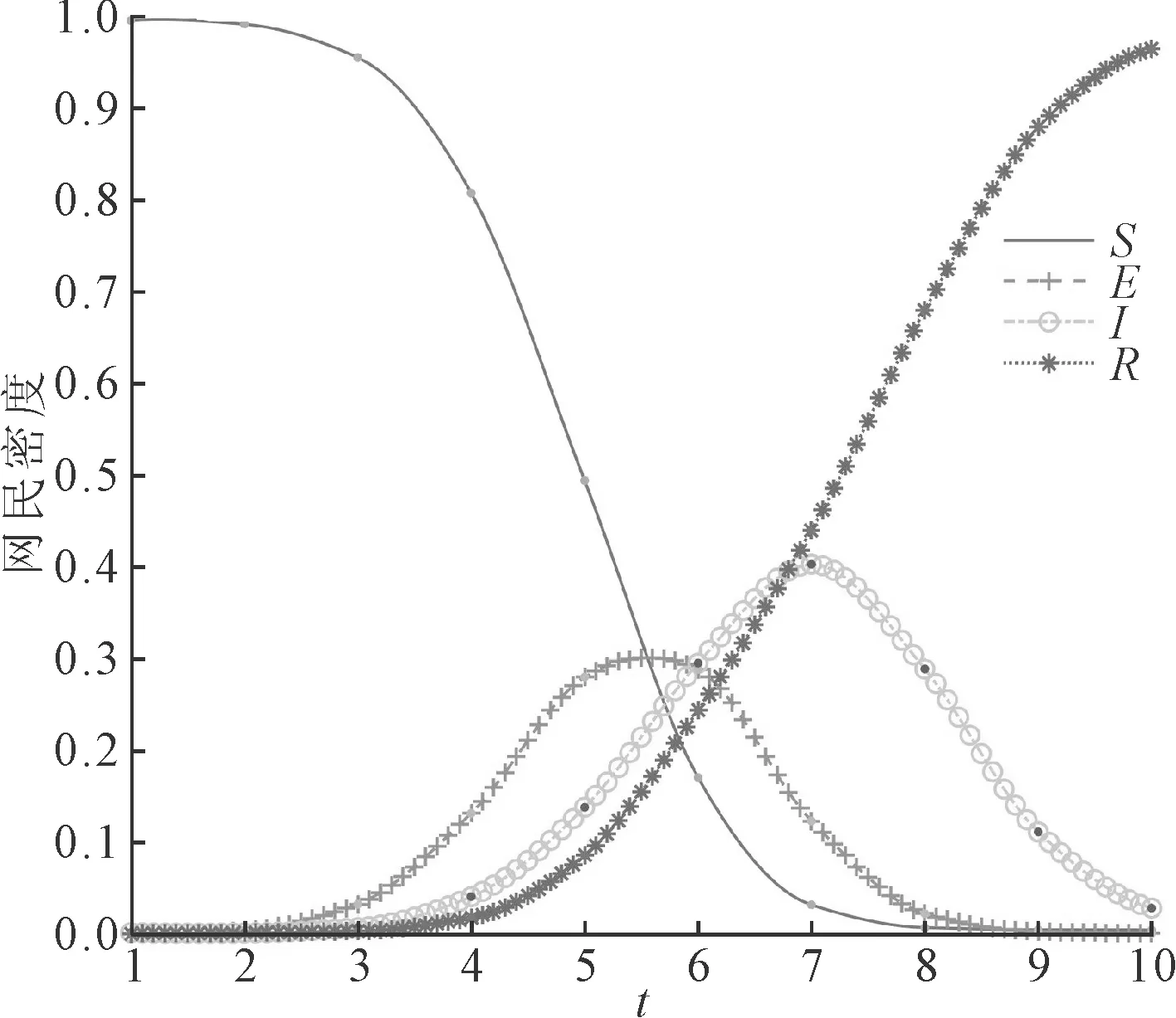
图10 I1>500实施干预下的舆情传播过程

3.2.2 干预次生舆情行为的作用

(1)有无干预次生舆情行为对比实验。在舆情事件爆发后，面对网络舆情在传播过程中诱发的次生舆情，政府可以通过解答网友关注的问题或辟谣等方式消减民众的揣测，抑制次生舆情的传播。由于次生舆情更多是代表民众在网络舆情事件中集中关注的一小部分，因此干预措施更具针对性，效果也会更好，但这些次生舆情被抑制之后，并不能显著影响原生舆情的传播。故认为政府针对次生舆情采取措施比针对原生舆情采取措施的实行效果更好，但是只对次生舆情有效，假设其干预系数为0.15。即α1=0.8，α2=0.2，α3=0.95，α4=0.05，β1=0.8，β2=0.5，β3=0.15，δ1=0.2，δ2=0.35，θ1=0.65，θ2=0.35，λ1=0.35，λ2=0.95，λ3=0.65，nc=2。次生舆情干预行为下的舆情传播过程如图11所示。对比图4、图9和图11可知，针对次生舆情的干预行为能够有效降低舆情峰值，但不能推迟舆情峰值到来的时间，且潜伏者数量的增长速度和未知者数量的下降速度也变化不大。这是因为在网络舆情爆发后，原生舆情一直是舆情传播过程中的主要信息，同时针对原生舆情采取的干预行为更早产生效果，遂导致次生舆情干预行为效果相对较差。

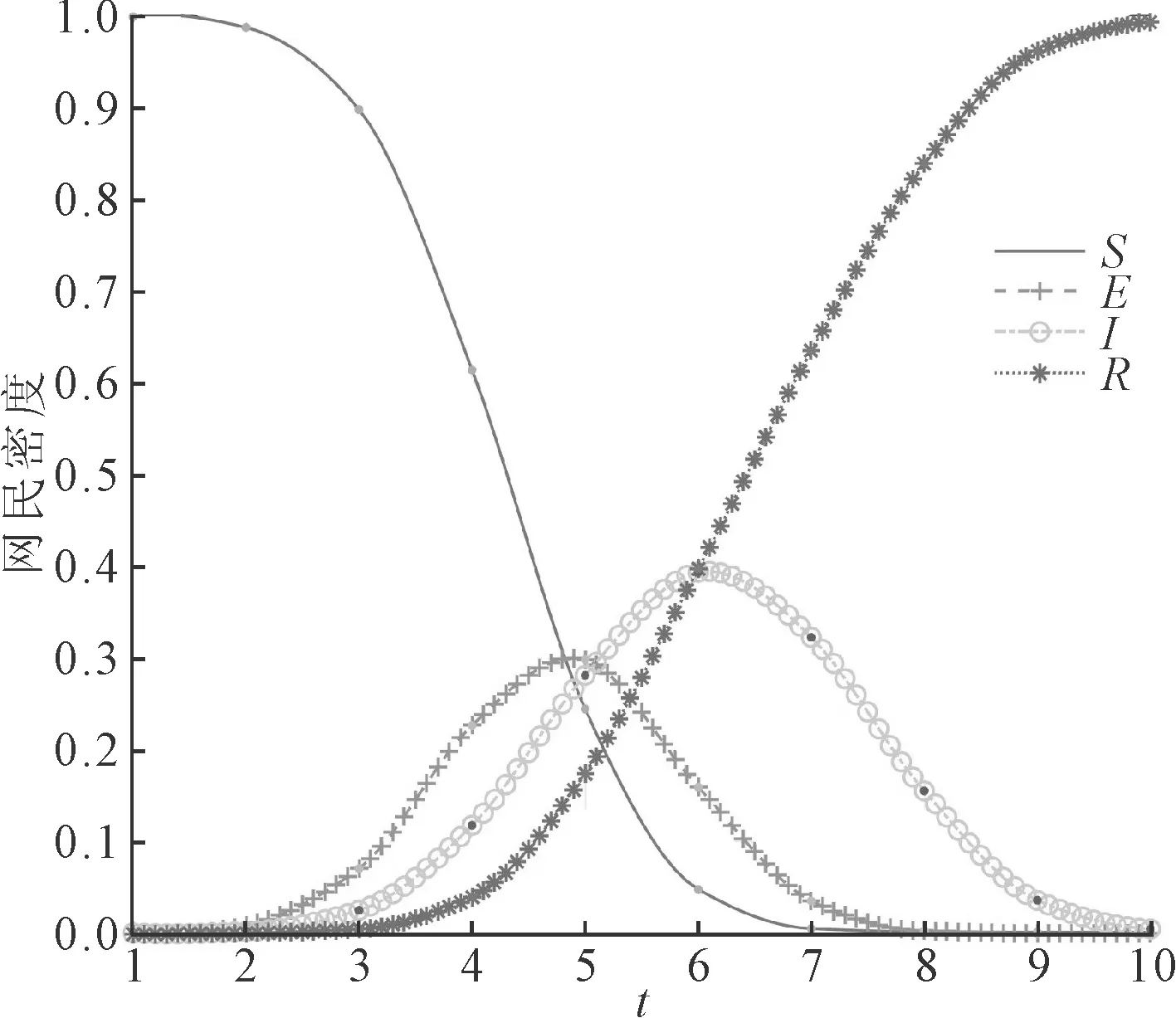
图11 次生舆情干预行为下的舆情传播过程

(2)不同时间点干预次生舆情对比实验。次生舆情爆发后，政府在不同时间节点发布权威信息，以削弱舆情传播，但是所起到的作用不尽相同。为了对比不同时间政府干预次生舆情的行为所产生的效果，观察I2节点数量变化规律后，设置如下传播机制：舆情传播初期，各传播参数采用基础参数组的数值；当舆情发展到一定时间，次生舆情传播节点数量I2>100时，政府干预次生舆情传播，各参数发生变化，此时的舆情传播过程如图12所示。对比图11和图12可知，在I2>100时政府实施干预，未知者数量下降更为缓慢，而潜伏者数量和舆情传播者数量增长更加迅速，舆情达到的峰值更高。显然，如果政府能够时刻关注舆情走向，在次生舆情出现初期，及时采取有效措施抑制次生舆情的扩散和传播，可以更加有效降低舆情事件的影响。

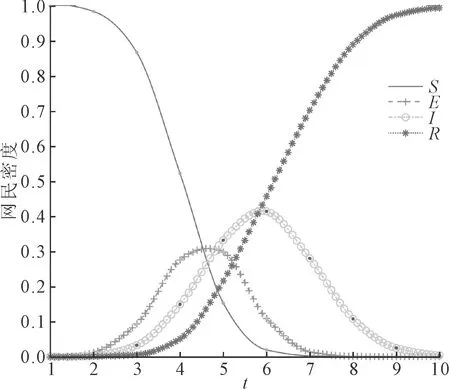
图12 I2>100时实施干预下的舆情传播过程

4 结论

(1)次生舆情影响下的舆情传播仿真结果表明，次生舆情能够推动舆情更快达到更高峰值并延长舆情持续时间，且次生舆情数量增加时，舆情峰值也会增长；在舆情传播后期次生舆情的爆发甚至会导致舆情反复，影响舆情治理效果。如果网友在接触舆情初期能先持观望态度，则舆情峰值会显著降低。

(2)政府干预下的舆情传播仿真结果表明，政府及时对舆情传播采取有效干预措施，能够降低舆情影响，延缓舆情高峰到来，为舆情管理部门争取更多时间，从而提升舆情治理能力与把控能力。

(3)基于传统SEIR建立考虑次生舆情影响的网络舆情传播模型，模拟了次生舆情影响下的网络舆情传播过程，较为全面地描述了舆情传播中所有参与网民的可能状态变化。但模型仿真仅考虑一次次生舆情的影响，但现实中多个次生舆情很可能是相继爆发的，它们的性质及对原生舆情的影响也不尽相同。且模型假设单位时间内网络节点间传播概率均等，这与实际情况并不一致，个体间的亲密度、舆情接收次数等均会影响传播概率，未来可以针对这些问题深入研究，并增加实例分析验证仿真结果，不断完善模型。