关于个体优势识别的区间q-Rung Orthopair模糊综合评价方法研究

吕皖慧，吕梦迪，林志超，周礼刚

(安徽大学 数学科学学院,安徽 合肥 230601)

群体或者个人的内部条件与外部条件共同影响个体优势，若片面地采用一个标准对事物进行评价，往往会忽略事物的个体优势而使所得评价不全面。因此，客观地识别个体优势，有利于个体了解自身优势、扬长避短，当对事物进行评价时，所得结果更令个体信服，这对于组织进步、社会协调也有着重要作用[1]。柳森等[2]在竞优思想的指导下，采用2-范数意义下的距离，提出一种基于层次结构的个体优势特征识别方法；赫连志巍等[3]从集群升级导向的角度探讨个体优势识别问题，根据目标规划的思想从最有利于被评价者的角度识别个体优势;杨锴等[4]使用VIKOR方法结合个体优势识别模型判别个体治理能力特征优势。这些研究从不同的角度出发解释了个体优势识别问题，但计算的指标都是精确值，然而在现实生活中由于人类的主观意愿以及对于事物认识的不全面，指标值往往是模糊数。

模糊集理论[5]最先是由美国加州大学ZADEH教授创立，即运用数学的方法解决模糊不确定的问题。学者们对此深入研究并提出很多理论分支，其中ATANASSOV[6]对模糊集的理论进行拓展，并提出直觉模糊集的理论。与传统模糊集不同，直觉模糊集同时考虑了隶属度、非隶属度与犹豫度，且需要满足隶属度与非隶属度之和小于等于1的约束条件。但是该约束条件对于解决更复杂的问题具有局限性，因此YAGER[7]对直觉模糊集进行了拓展，提出了Pythagorean模糊集理论且满足隶属度与非隶属度平方的和小于1，大大扩充了直觉模糊集的范围。然而Pythagorean模糊集在生活中仍存在局限性，YAGER[8]在此基础上进一步提出了q-Rung Orthopair模糊集概念，以隶属度与非隶属度q次方之和小于1作为约束条件。区间q-Rung Orthopair模糊集[9]则是Orthopair模糊集概念的引申，其中隶属度和非隶属度由一个区间值给出。对于多属性决策问题，由于实际生活中决策信息日渐复杂，决策者不能明确给出各属性信息，往往以区间自然形式给出[10]，利用区间q-Rung Orthopair模糊理论衡量信息间的差异程度。

因此，笔者提出一种新的关于个体优势识别的区间q-Rung Orthopair模糊多属性决策问题的评价方法。根据赵希男等[11]对于个体优势识别的示例，定义了一种绝对值加权区间q-Rung Orthopair模糊距离测度，依据个体优势的理想点模型下距离测度的应用，利用数学规划的方法求出各属性权重，结合求得的距离与属性权重计算自评值与他评值，取其算术平均值计算综合评分值；定义各距离测度的相对大小为专家权重，利用加权平均的方法计算各个决策单元最终的综合评价值，通过排序选出最优方案；最后将这种方法应用到高校人才引进方案中，对于高校招聘人才、提高教学质量与教师素质、提升高校综合实力具有一定的参考价值。

1 预备知识

定义1令X是一个已知的论域，则X上的直觉模糊集可表示为A={[x,μA(x),vA(x)]|x∈X}。其中，对于一个给定的x∈X，μA(x)和νA(x)分别表示元素x属于X的隶属度和非隶属度，且满足μA(x)、νA(x):X→[0,1],0≤μA(x)+νA(x)≤1；定义A中元素x属于A的犹豫度为πA(x)，则X上的直觉模糊集的犹豫度为πA(x)=1-[μA(x)+vA(x)],易见0≤πA(x)≤1。

针对直觉模糊集无法表达隶属度和非隶属度之和大于1的情况，2013年YAGER提出Pythagorean模糊集；为进一步扩大隶属度和非隶属度的空间范围，YAGER于2017年提出q-Rung Orthopair模糊集的概念。

定义2令X为一个已知的论域，则X上的q-Rung Orthopair模糊集可以定义为A={[x,μA(x),vA(x)]|x∈X}。其中，对于一个给定的x∈X，μA(x)和νA(x)分别表示元素x属于X的隶属度和非隶属度，且满足μA(x)、νA(x):X→[0,1]，0≤(μA(x))q+(vA(x))q≤1，q≥1；定义A中元素x属于A的犹豫度为πA(x)，则X上的q-Rung Orthopair模糊集的犹豫度为πA(x)=(1-[(μA(x))q+(vA(x))q])1/q，易见0≤πA(x)≤1。

为简化计算过程，对于一个给定的x∈X,称(μA(x),vA(x))为q-Rung Orthopair模糊数，表示为(μA,vA)。当q=1时，A为直觉模糊集；当q=2时，A为毕达哥拉斯模糊集。区间q-Rung Orthopair模糊集的概念又由q-Rung Orthopair模糊集引申而来。

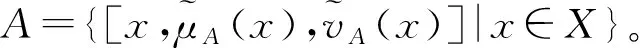
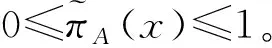
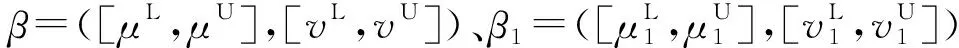
根据以上运算法则可以得到如下结论：①β1⊕β2=β2⊕β1；②t1β⊗t2β=(t1+t2)β；③t(β1⊕β2)=tβ1⊕tβ2；④(βc)c=β。其中，t、t1和t2为任意常数。

2 一种绝对值加权区间q-Rung Orthopair模糊距离测度

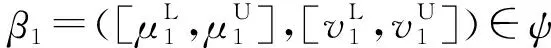
(1)

将dμ(β1,β2)、dv(β1,β2)代入后化简可得d(β1,β2)为:

(2)

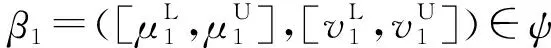
证明在[μL(x),μU(x)]⊆[0,1]，[vL(x),vU(x)]⊆[0,1]前提下，结果①、②显然成立，下面证明结果③，对于结果③应用绝对值不等式可得：

∵(d(β1,β)+d(β,β2))q≥dq(β1,β)+dq(β,β2)=

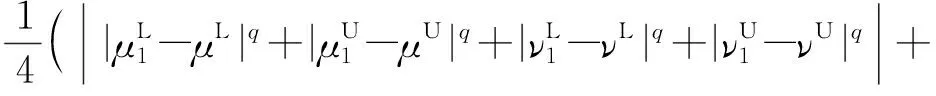
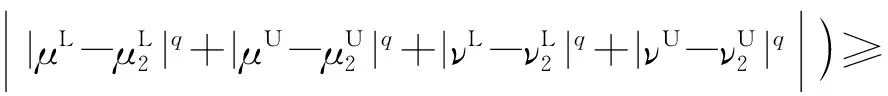
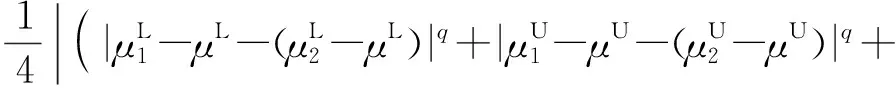
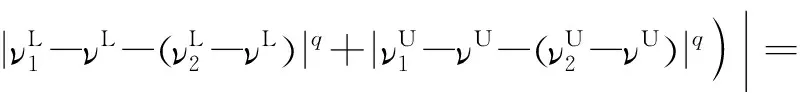
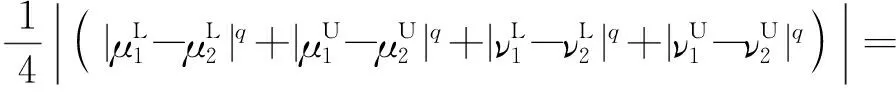
dq(β1,β2)

∴d(β1,β)+d(β,β2)q≥dq(β1,β)+dq(β,β2)≥dq(β1,β2)

∴d(β1,β2)≤d(β1,β)+d(β,β2)

证毕。

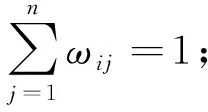
(3)

3 关于个体优势识别的区间q-Rung Orthopair模糊多指标综合评价

当对几种类型相同或相似的群体或个别主体的状态属性进行综合评价时，由于事物较为复杂，主体的状态属性一般由多个指标构成。为实际应用过程的便利，假设刻画这些主体的指标为效益型，即在符合社会道德标准与基本要求的前提下，指标值越大越好。

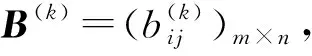
(1)数据标准化处理。由于各指标的基本属性不同，为消除不同量纲的影响，对原始数据进行标准化。由于区间q-Rung Orthopair模糊数区间隶属度、区间非隶属度均属于[0,1]，区间犹豫度大小介于0～1之间，所以初始数据即理想标准化处理后所得的结果。

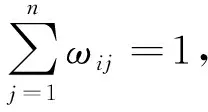
(4)

(3)理想点模型的建立。已知距离越小，主体的评价值越接近理想点，从最有利于每个主体的想法出发，与理想点越近的指标应赋予越大的权重；反之，当距离理想点越远，说明指标相对较差，应赋予较小的权重来平衡所得评价值。因此可建立数学规划模型：

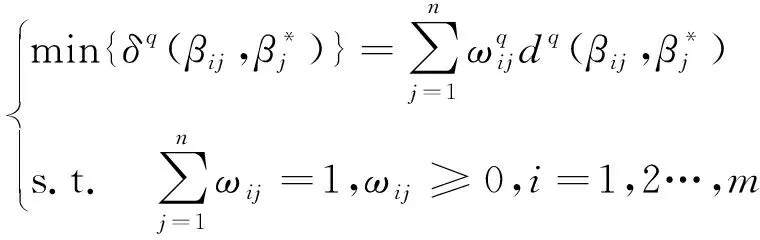
(5)

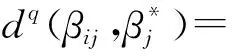
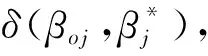
(6)

(7)

最后综合自评值和他评值为民主代理评价值，取所有评价值的算数平均值，此时包括对于所有主体评价的不同意见。其优点是评价结果较客观、容易获得全部主体的认可。已知距离越小，主体的评价值越接近于理想点，故民主代理评价值越小越好。民主代理评价值的计算方法为：

(8)

(6)专家权重的确立。根据第k个决策者与l个决策者给出评价值之间的平均值距离测度定义专家权重为ν=(ν1,ν2,…,vl)T[14]：

(9)

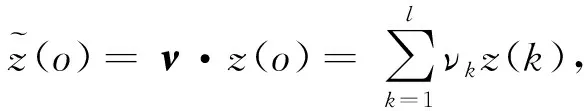
4 案例分析

在国家实施人才强国战略和自主创新战略的背景下，中央批准了一项海外高层次人才引进计划，其中高层次人才引进工作中能否达到预期效果，优秀工作者的选择与判定是最重要的基础工作[15]。某高校计划从海外引进杰出人才，组织了一个由3位专家构成的评估组，分别为学校校长g1、管理学院院长g2和人事处处长g3。为了学校能够引入全方面较为优秀的人才，评估组准备从思想品德(c1)、科研能力(c2)、教学技能(c3)和教育背景(c4)4个方面对5位候选者x1、x2、x3、x4、x5进行相应的审核并选择最优的候选者作为人才引进对象。各个决策者给出的区间q-Rung Orthopair模糊决策矩阵B(k)为：

(1)数据标准化处理。由于每个候选人的指标信息为区间q-Rung Orthopair模糊数，且区间隶属度、非隶属度均属于[0,1]，区间犹豫度的大小均介于0～1之间，所以无需标准化处理。

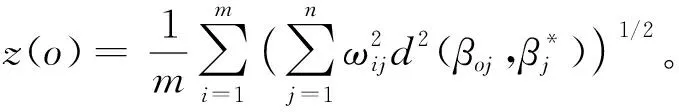
(3)根据理想点模型计算权重。以决策者学校校长g1对应的决策矩阵B(1)和第一位候选者x1为例，根据距离与权重的相关定义求解得到：

|0-0.1|2+|0-0.2|2)|=0.062 5

|0-0.4|2+|0-0.5|2)|=0.352 5

|0-0.2|2+|0-0.3|2)|=0.095 0

|0-0.2|2+|0-0.4|2)|=0.202 5

(4)计算民主代理评价值。若每位候选者的自评值和他评值构成一行，那么5位候选者的自评值和他评值构成5×5的矩阵Z1，其中矩阵对角线上的元素为自评值，其他元素为他评值，第i行的其他元素表示其他候选者对于候选者xi的他评值，第i列其他元素表示候选者xi对于其他候选者的他评值。以由式(6)和式(7)分别计算5位候选者的自评值和他评值，进而得到评价值矩阵Z1：

再根据式(8)计算在决策者g1对应的决策矩阵下各候选者的民主代理评价值：z1(1)=0.298 9，z1(2)=0.212 9，z1(3)=0.403 3，z1(4)=0.267 1，z1(5)=0.326 9。

(5)计算各个决策者的综合评价值。同理，可计算得到其他决策者对应的评价值矩阵和民主代理评价值(如表1所示)。

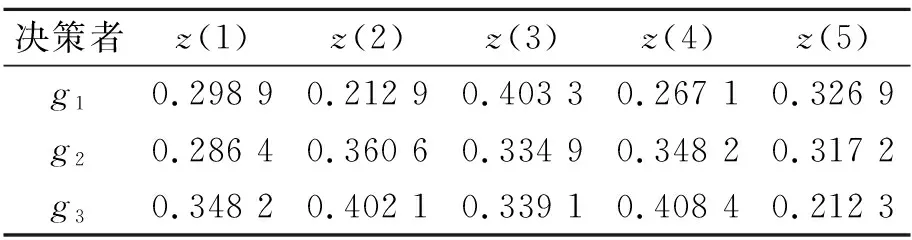
表1 各方案下的民主代理评价值

(6)专家权重的计算。由式(9)计算专家权重为ν=(0.334 1,0.335 0,0.330 9)T。

4.1 灵敏度分析

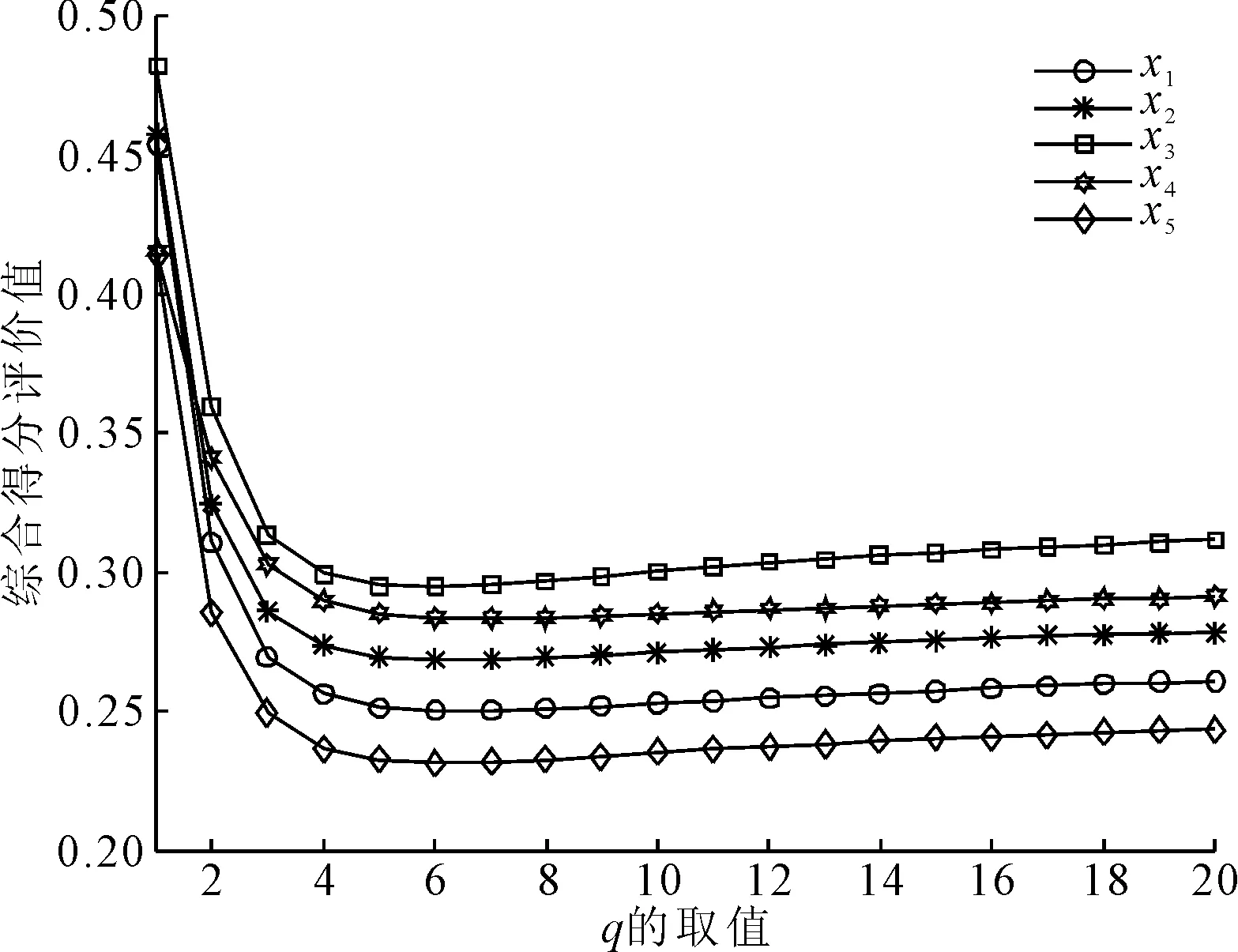
图1 综合得分评价值变化趋势图

4.2 对比分析

为了说明所提出方法的有效性，与文献方法进行比较，具体结果如表2所示。由表2可知，笔者所提方法得到的最优方案与文献[15]提出的区间直觉模糊群决策方法结果相同，相较于文献[17]中提出的专家与特性优先级不同的间歇性直觉模糊群体决策方法与文献[18]中提出的属性权重已知的群决策方法而言，不确定属性下权重的解决也比较重要，新提出的方法能够有效解决未知权重情况下的群决策问题。通过区间q-Rung Orthopair模糊综合评价优化模型计算不同下最有利于主体的权重系数，为最终判断主体优势从而做出专家决策提供依据。

表2 不同决策方法的决策结果比较

同时，笔者所提方法无需计算得分函数与精度函数，减少了评价过程的繁琐度与计算量，同时包含了自身及其他人的评价值，能站在不同的角度发现每个个体各自的优势和劣势，有利于实现人才的综合管理，在选择结果上更加公平公正，有利于做出正确决策。此外，相较于文献[15]和文献[17],新提出的关于个体优势识别的区间q-Rung Orthopair模糊综合评价方法是对已有区间直觉模糊决策方法的一种推广，决策者可以按照实际情况选择合适的参数q，因此这种方法更具有普适性。

5 结论

在新的区间q-Rung Orthopair模糊距离测度基础上，提出了关于个体优势识别的区间q-Rung Orthopair模糊综合评价方法及应用。与传统优势识别相比，能更好地处理指标值为区间q-Rung Orthopair模糊数的情况，无需主观判断给定每个指标的权重向量，且能够综合自评值与他评值，大大减少了因为自评主观臆断造成评价结果的不全面，使得评价择优结果更加公平公正，同时无需计算得分函数与精度函数，简化了评价步骤。最后通过参数q敏感度分析可知候选者x5的评价值始终最好，且各个候选者的评分值随着参数q的增加先减小后逐渐增大至q为某个值时各个候选者的评分值趋于稳定。新的关于个体优势识别的多属性决策方法可以进一步推广，运用于公司人才选拔、城市人才引进、股票市场优股的选择、医药产品的评估等领域中。