重载钢轨摩擦热损伤行为研究

2022-01-20徐培娟张大伟田抑阳钟琛

铁道科学与工程学报 2021年12期

徐培娟，张大伟，田抑阳，钟琛

(1.长安大学运输工程学院，陕西西安 710064；2.长安大学汽车学院，陕西西安 710064；3.西南交通大学牵引动力国家重点实验室，四川成都 610031；4.重庆市轨道交通(集团)有限公司，重庆 401120）

重载铁路运输作为国际上公认的铁路运输尖端技术之一，代表着铁路货物运输领域的先进生产力。而随着重载货物运输的快速发展，重载铁路逐渐暴露出诸多问题，其中，钢轨伤损问题日益加剧，这对重载铁路的正常服役和列车运行安全带来了严峻的挑战。为了揭示轮轨损伤机理，一直以来重载轮轨关系受到了各国专家学者的重点关注，力图减少钢轨的劣化损伤，并延长钢轨的使用寿命。目前，对于重载轮轨损伤的研究，主要集中在轮轨接触界面的磨耗[1-2]和疲劳损伤[3]2个层面。仅有一部分学者开始关注轮轨的热伤损问题，对轮轨滑动生热问题做了初步的探索。如吴磊等[4-5]基于有限元方法和移动热源法，建立了轮轨摩擦非稳态传热计算模型，发现轮载、摩擦因数和相对滑动速度对钢轨摩擦温升有显著的影响。NAEIMI等[6]建立了三维轮轨弹塑性模型，研究了大蠕滑下的轮轨温度变化，证实了钢轨材料相变的可能性。ALIZADEH等[7]分析了车轮踏面扁疤存在下的轮轨温度演化行为。另外，SPIRYAGIN等[8]则基于解析法构建了轮轨温升模型，借助车辆的多体动力学实时获得轮轨动态温度变化。杨新文等[9]则进一步应用热传导经典方程式来分析轮轨滑动生热过程中的钢轨表面材质的热相变行为。可见，对于轮轨热损伤这一科学问题的研究，目前仍处于初步探索阶段，尚缺乏对重载轮轨复杂接触行为的准确描述，以及对轮轨系统中的热传导过程也认识不足。为了更加合理地分析轮轨的热损伤行为，本文采用半赫兹理论[10-13]求解轮轨接触行为，并借助热传导理论分析轮轨滑动过程中的热传导过程，以相变过程中的钢轨材质硬化深度表征轮轨损伤状态，进一步分析钢轨型面、轨底坡和摩擦因数对钢轨硬化损伤的影响。

1 轮轨热力耦合模型

1.1 轮轨半赫兹理论

对于轮轨法向接触行为，赫兹理论已广泛应用于车辆动力学仿真中。根据赫兹理论的基本假设，当2个弹性体相互压缩时，需满足以下条件：弹性接触行为；半无限空间；接触斑尺度远小于接触界面的轮轨曲率半径且轮轨曲率半径为定常曲率。然而，以上假设条件并不总是成立，由于接触斑内轮轨截面并不总是保持定常曲率半径，因此接触斑并不总是表现为椭圆形状。另外，小半径曲线上车轮轮缘与钢轨轨距角时有接触，轮轨接触界面的曲率半径与接触斑尺度相近。磨耗后的轮轨接触更为复杂，常常伴随共形接触的发生。在上述几种情形下，采用赫兹理论往往得不到合理的结果。为此，如何合理地表征轮轨接触行为，对于研究轮轨动力相互作用以及轮轨磨耗具有十分重要的意义。尽管KALKER已经建立了较为完善的三维轮轨滚动接触模型，并开发了相应的计算程序CONTACT，由于其求解效率较低，将其应用于车辆动力学以及车辆—轨道耦合动力学数值研究中仍然十分困难。因此，采用更加高效的轮轨求解方法解决重载工程问题愈发重要。

为了解决非定常曲率等复杂接触条件下的轮轨接触行为，AYASSE等[12-13]基于赫兹理论提出了一种半赫兹求解方法，本文正是基于该方法求解重载轮轨法向接触行为。

图1给出了半赫兹轮轨接触的基本求解方法。O-XYZ坐标系为随轮对运动的刚体坐标系，坐标原点位于轮对轴线的中心，X轴沿轮对运行方向，Y轴沿轮对中心轴方向，Z沿铅锤方向。zpw(y)表示YZ平面内的车轮横截面曲线，zpr(y)表示Y-Z平面内的钢轨横截面曲线。假设h0=-ε0z0，z0表示为轮轨接触最大压缩量，h0表示为车轮踏面最大压缩量，ε0为修正的压缩系数，因此钢轨表面的最大压缩量为z0+h0。将接触斑沿y轴划分为n个区间，第i个区间的坐标为yi，该坐标处的钢轨压缩量可表示为：

图1 半赫兹轮轨接触求解示意图Fig.1 Solution method of semi-Hertzian

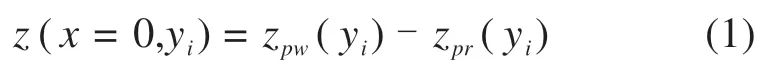
且每个条带上的压缩量应满足：

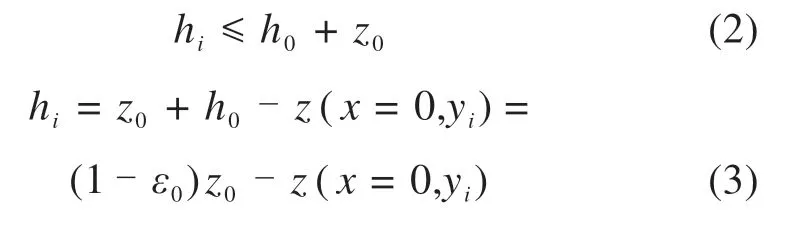
每个条带上的修正系数可由每个条带上的赫兹系数n，r，A，B来表示：

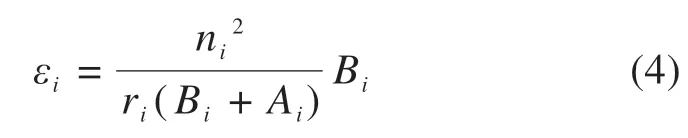
因此，ε0=max(εi)。

为了得到每个条带上沿x轴方向的长度ai，需满足-hi+≤0，于是，

式中：为修正的相对曲率。得到每个条带沿x轴方向的长度后，即可得到轮轨接触斑。进而，轮轨接触斑内的法向压力可表示为：

式中：Es和vs分别表示为钢材质的杨氏模量和泊松比。对法向应力积分可得到轮轨法向力为

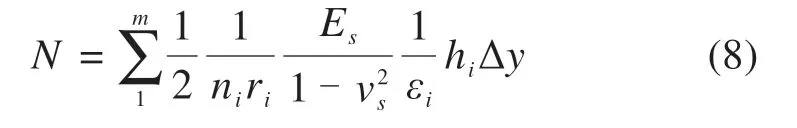
式中：Δy为条带的宽度。

1.2 轮轨切向行为

机车车辆在牵引或者制动条件下，往往伴随较大的滑动率，甚至在牵引力不足的情况下，发生车轮打滑现象，严重的会导致车轮踏面擦伤。车辆在运行过程中摩擦因数也会随相对滑动速度的增大而有所降低[14]。为此，本文考虑了大蠕滑条件下的轮轨切向作用，采用文献[15]提出的方法，纵向蠕滑力可表示为：

式中：fx为纵向方向上的黏着系数，可表示为，

式中：a，b为赫兹理论计算得到的接触斑椭圆的长半轴和短半轴；μ为动摩擦因数；μ0为静摩擦因数；Δv为接触点处的相对滑动速度；A为动静摩擦因数比值；B为指数衰减系数；C11为Kalker线性理论值；kA和kS为缩减因子；s为沿纵向上的蠕滑率。

如图2所示，黏着系数随车辆运行速度和蠕滑率的变化情况，对应式(10)～(12)中参数取值如下：kA=1，kS=0.4，μ0=0.45，A=0.4，B=0.6。可以发现，在高速大蠕滑率条件下，黏着系数有下降的趋势。

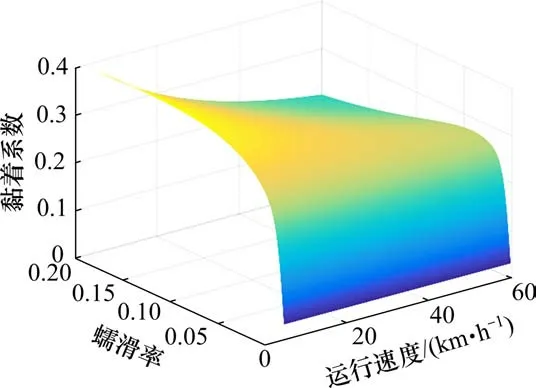
图2 黏着系数随速度和蠕滑率的变化情况Fig.2 Variation of the adhesion coefficient with the velocity and creepage rate

1.3 轮轨摩擦热传导

轮轨滑动过程产生的热量可表示为：

式中：q(x,y)为热流密度，J/(m2·s)；p(x,y)为接触区法向压力分布；Δv为轮轨相对滑动速度；fa表示传递至钢轨热量占摩擦总热量的比重，不考虑热量在空气介质中的传播且认为传递到钢轨和车轮的能量相同，于是fa可取为0.5。

由于轮轨接触斑远远小于钢轨表面的尺寸，且接触斑热量在有限空间内传递，因此可将钢轨视为半无限空间，并建立基于各向同性固体的热传导经典方程式，即

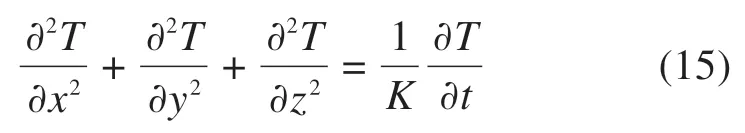
式中：T表示温度；(x,y,z)为空间坐标点；K为热扩散率。代入移动热源后可得到，

式中：cp表示比热容；k为热传导率；ρ为钢轨密度；(x,y)为接触斑离散热源坐标。

本文将接触斑分为M×N个区间，每个区间上的热功率为Q=qi,jdxdy，并计算该作用力在t时间内产生的热量及引起的轨温升高，最后将所有区间上引起的钢轨半空间内温升叠加即可得到接触斑在有限空间内引起的轨温升高量。

具体计算流程如图3所示，为获取t时刻的温度场分布，定义离散积分步长为dt，总的离散时间数为Nt=t/dt。

图3 钢轨温度分布计算流程Fig.3 Calculation flow chart of the rail temperature distribution

在初始点时，热源qi,j,1坐标点为(x+dtV,y)，引起t时刻的温度分布为dTi,j,1(X,Y,Z,Ntdt)；在第2个积分步长dt，热源qi,j,2坐标点为(x+2dtV,y)，在t时刻的温度分布为dTi,j,2(X,Y,Z,Ntdt-dt)；在第3个积分步长dt，热源qi,j,3坐标点为(x+3dtV,y)，在t时刻的温度分布为dTi,j,3(X,Y,Z,Ntdt-2dt)，以此类推，得到该单个移动热源产生的总温度分布场为

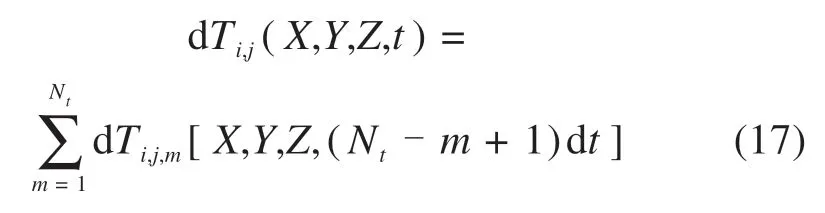
因为有M×N个离散热源，因此总的温度场分布为

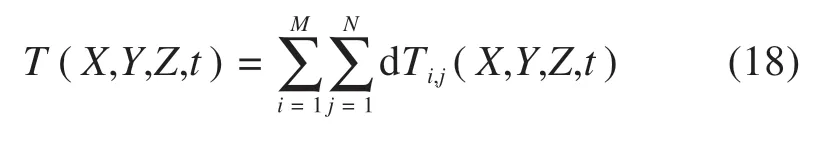
在机车车辆牵引及制动条件下，轮轨打滑必然引起轮轨接触界面的温度急剧升高，当温度达到相变温度(750℃)时，钢轨表面材质开始向奥氏体转变，而当车轮通过后，温度的急剧下降引起奥氏体转变为脆硬的马氏体。这种马氏体组织易在重复轮轨荷载作用产生裂纹，甚至发生剥离。因此，本文将由轮轨摩擦升温引起的钢轨表面材质转变的硬化深度作为衡量钢轨损伤的重要指标进行分析研究。

2 重载轮轨接触行为分析

为了掌握重载轮轨接触行为的变化情况，利用半赫兹接触理论，对不同车轮横移量、轨底坡条件下的轮轨接触斑形貌以及接触压力进行分析。计算条件为：LM车轮踏面，CN75钢轨型面，1:40和1:20 2种轨底坡，轴重为30 t，不考虑动荷载。

如图4所示，给出了3种条件下的轮轨接触斑形貌和接触应力。图4(a)为车轮无横向移动、轨底坡为1:40条件下的轮轨接触斑形态，可见其基本表现为椭圆形，最大压力为2 070 MPa；图4(b)为轮对横向移动5 mm条件下的轮轨接触斑状态，其形状已经开始向非椭圆形转化，最大压力可达2 750 MPa；图4(c)为车轮横向移动5 mm，轨底坡为1:20条件下的轮轨接触斑，其沿y轴方向上的长度明显比1:40轨底坡下的要大，接触面积显著增大，最大压力降低至1 760 MPa。

图4 重载轮轨接触行为Fig.4 Contact behaviour between the wheel and heavy rail

由上述结果可知，重载轮轨接触斑形貌随接触条件的不同发生了显著地变化，明显由椭圆形向非椭圆形转变。显然，利用赫兹接触的椭圆形接触斑来描述重载轮轨行为必然导致较大的误差，而半赫兹轮轨接触理论的引入为合理求解轮轨接触行为提供了一种思路。

3 重载轮轨热力损伤特性分析

利用半赫兹理论得到轮轨法向应力分布，可得到轮轨切向应力分布，进而利用热传导理论即可得到轮轨滑动条件下的钢轨温升分布规律。轮轨参数采用上节的基本参数，其他热力学参数见表1，其中，钢轨材质的相变温度为750℃。

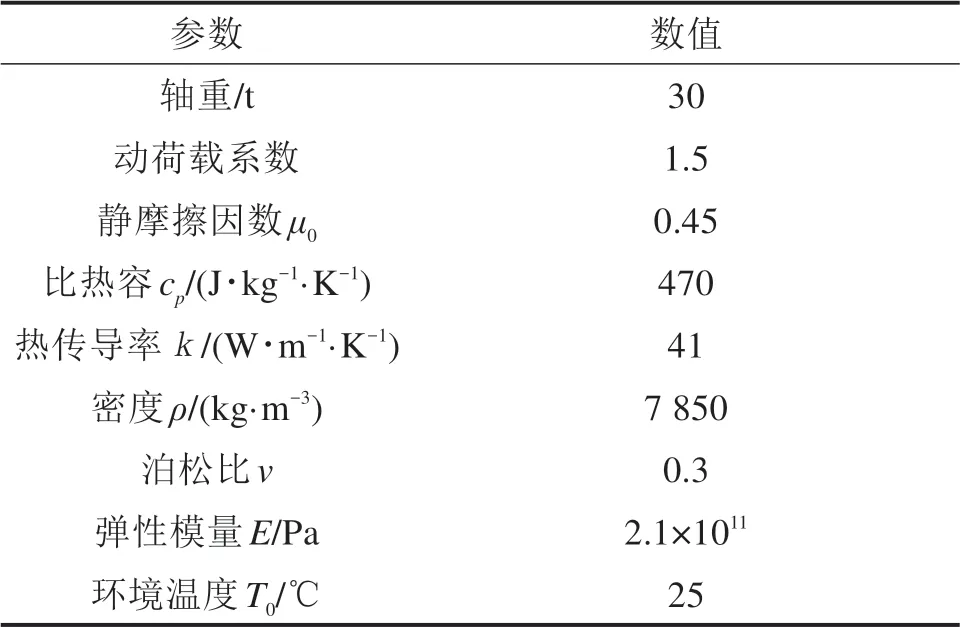
表1 轮轨热力学基本参数Table 1 Thermology parameters of wheel/rail system

图5给出了当速度为20 km/h，蠕滑率为0.1时，钢轨内部及表面的温度分布规律，可以发现，此时钢轨表面的最大温度已经超过750℃，也就是大于钢轨材料的相变温度，因此必然会引起钢轨硬化现象的发生。图6则给出了蠕滑率为0.1时，速度对钢轨表面温度分布的影响，可见当运行速度由40 km/h提高到60 km/h时，钢轨表面由轮轨摩擦生热引起的热影响区将明显增大，同时，高温区域面积也存在增大的趋势，亦即，速度提高会造成钢轨相变区面积的增大。

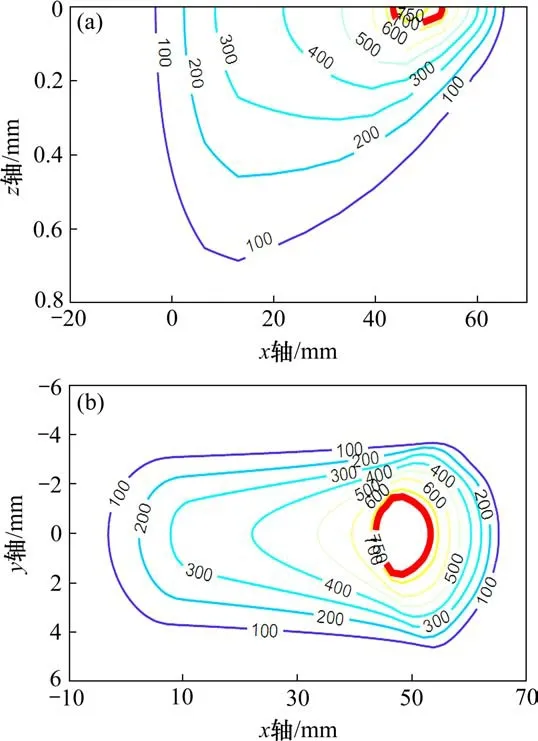
图5 钢轨温度的分布规律(运行速度20 km/h，蠕滑率0.1)Fig.5 Temperature distribution of the rail with the creepage rate of 0.1 at the speed of 20 km/h

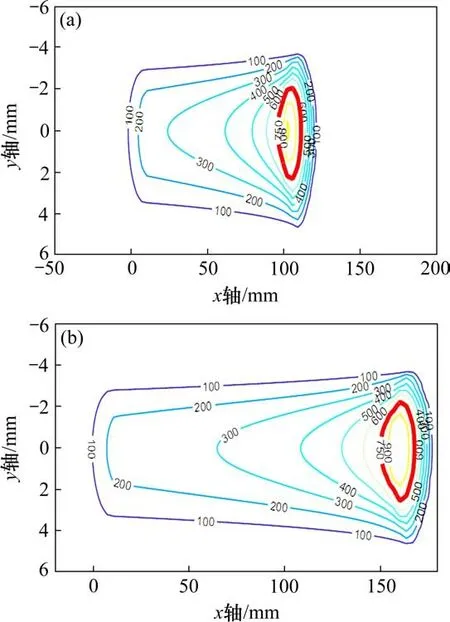
图6 不同速度下的钢轨表面温度分布Fig.6 Temperature distribution of the rail surface with different running speeds

为了研究速度对钢轨硬化的影响，图7给出了不同速度下的钢轨硬化深度的变化。由图中可知，蠕滑率由0增加到0.2时，10 km/h的运行速度对应的钢轨硬化深度由0 mm增大到0.23 mm；20 km/h车辆运行速度对应的钢轨硬化深度由0 mm增大到0.21 mm；40 km/h车辆运行速度对应的钢轨硬化深度由0 mm增大到0.17 mm。总体来看，大蠕滑率下，运行速度越低，导致的钢轨硬化深度越大，对钢轨的损伤越大。因此，低速牵引及制动条件下，应避免大蠕滑率情况的发生，这对于钢轨热损伤的缓解具有积极的作用。同时，也可发现，速度越高，引起钢轨硬化的初始蠕滑率也越低，亦可说明，高速低蠕滑率下也有可能引起钢轨硬化现象的发生。

图7 速度对钢轨硬化的影响Fig.7 Effect of the running speed on the rail hardening

另外，随着我国重载运输的发展，增大轴重势在必行，而轴重的增大，势必加剧轮轨动力作用，也必然对钢轨的损伤带来不利影响。为此，图8给出了不同轴重对钢轨硬化深度的影响，分析的车辆运行速度为40 km/h，蠕滑率分别为0.1，0.15和0.2。由图中可见，轴重从25 t增加到30 t，不同蠕滑率对应的钢轨硬化深度均有所增加，3种蠕滑率下分别增大了34%，17%和14%。上述结果也说明轴重的增加，势必加速钢轨硬化的发生。

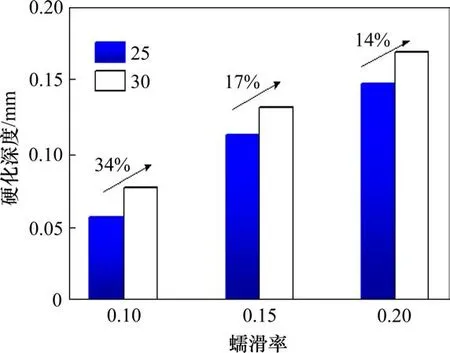
图8 轴重对钢轨硬化的影响Fig.8 Effect of the axle load on the rail hardening

4 轮轨参数的影响研究

为了控制大蠕滑率状态下的轮轨热损伤行为，有必要对不同条件下的钢轨硬化行为进行分析研究。本节主要针对不同的钢轨型面、轨底坡以及轮轨摩擦因数等条件，以钢轨硬化深度为量化指标，寻求减轻轮轨热损失的有效方法。

4.1 钢轨型面的影响

对于钢轨型面的优化研究，一直以来都是重载铁路的研究方向。钢轨型面的设计是一个复杂的工程，涉及诸多因素，包含减缓轮轨磨耗，改善接触状态[16]，减轻轮轨动作用力和轮轨损伤等多方面。本节仅从滑动条件下的钢轨热力硬化损伤的角度出发，研究轮轨大蠕滑条件下，不同钢轨型面对钢轨硬化深度的影响。

主要的分析条件如下：车辆的运行速度为40 km/h，相对滑动速度为2 m/s，轨底坡为1:40，2种钢轨型面分别为CN75轨和CN60轨。如图9所示，不难看出不同的钢轨型面对钢轨硬化深度的影响较为明显，不同横移量下的CN60钢轨的硬化深度都有不同程度的下降。需要说明的是车轮向轨道外侧运动时横移量为正值，向轨道中心侧运动时横移量为负值，3种横移量-5，0和+5 mm下，CN60轨同CN75轨相比，钢轨硬化深度分别下降了23%，10%和48%。可见，以钢轨硬化深度指标分析，CN60轨更有利于减轻轮轨热力损伤。

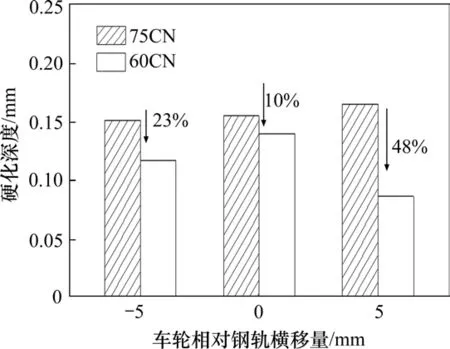
图9 钢轨型面对钢轨表面硬化深度的影响Fig.9 Effect of the rail profile on the depth of the rail hardening

4.2 轨底坡的影响

轨底坡对轮轨接触行为也有着显著的影响，也必然对轮轨热损伤产生一定程度的影响。仅从钢轨热力硬化损伤的角度出发，探讨轮轨大蠕滑条件下，不同轨底坡对钢轨硬化深度的影响。主要的分析条件如下：车辆运行速度为40 km/h，相对滑动速度为2 m/s，钢轨型面为CN75轨，轨底坡分别为1:40和1:20。结果如图10所示，可以看到不同车轮横向移动状态下的钢轨硬化深度受轨底坡的影响较为明显，3种横向量下的钢轨硬化深度分别变化了4%，-100%和-50%，总体来看，轨底坡增大，轮轨热伤损是有所降低的。因此，从降低钢轨热伤损的角度出发，CN75钢轨宜采用1:20的轨底坡。

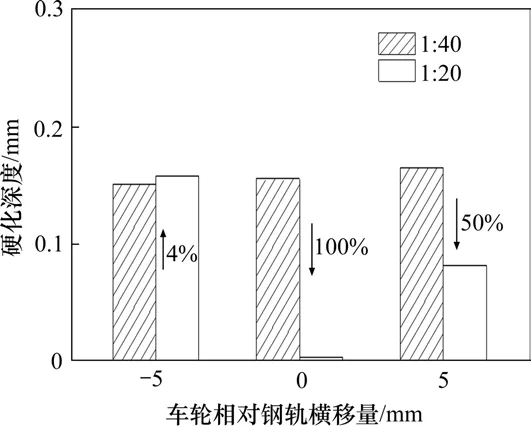
图10 轨底坡对钢轨表面硬化深度的影响Fig.10 Effect of the rail cant on the depth of the rail hardening

4.3 摩擦状态的影响

同样地，钢轨表面摩擦因数在干燥和湿润条件下轨底坡对轮轨接触行为有着显著的影响。为了探讨轮轨大蠕滑条件下，不同摩擦因数对钢轨硬化深度的影响，具体的分析条件如下：车辆运行速度为40 km/h，相对滑动速度为2 m/s，钢轨型面为CN75轨，轨底坡分别为1:40，摩擦因数分别为0.45(干燥环境下)和0.25(湿润环境或润滑条件下)。如图11所示，可以发现不同车轮横移量下的钢轨硬化深度受摩擦因数的影响非常明显，3种横向量下的钢轨硬化深度分别下降了70%，68%和58%。总体来看，摩擦因数降低，轮轨热伤损是显著降低的，亦即从缓解钢轨热伤损的角度出发，钢轨润滑是有利的。