多分辨率增强能量算子的轴承微弱故障特征提取

刘志刚，张龙，胡俊锋，熊国良

(1.江西交通职业技术学院，江西 南昌 330013；2.华东交通大学 机电与车辆工程学院，江西 南昌 330013；3.中国铁路南昌局集团有限公司 科学技术研究所，江西 南昌 330002）

1 方法介绍

1.1 能量算子解调(TEO)

设连续信号x(t)的能量算子Ψ定义为；

针对离散时间信号x(n)，其Teager能量算子将变换为：

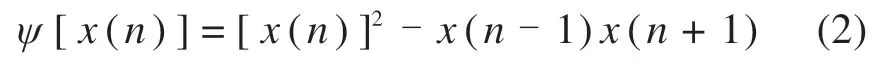
由式(2)可知，若要计算出离散时间信号y(n)的Teager能量算子，仅需知晓时刻n处的3个采样点便可。由此可见，Teager能量算子对于信号中的瞬态变化十分敏感，拥有十分优异的时间分辨率。

同理，若将随机离散信号x(t)定义为：

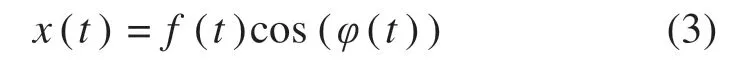
则该信号的能量算子定义为：

其 中：x(n)=f(n)cos(φ(n))；Ω(n)=φ(n)-φ(n-1)

由式(4)可知，TEO能够有效分离信号中的频率与振幅信息，但对于轴承故障而言，故障信息表征于振幅与频率中由故障脉冲引发的瞬态冲击特征，频率与振幅信息的分离并不必要。众所周知，TEO对于由机械故障引发的瞬态冲击特别敏感，故障冲击集中在一个短间隔的高频带中，相对其他如齿轮啮合、轴不平衡和背景噪声干扰而言，更强调故障的瞬态特性[10]。然而，TEO对于高信噪比条件下的异常脉冲敏感度高，但是对于低信噪比的信号而言，TEO的消噪性能并不理想，且经过TEO处理后的信号极易出现负值现象[11]。MTEO便能够解决以上问题。

1.2 多分辨率能量算子解调(MTEO)

基于离散信号的MTEO定义为：

对80例疑似甲状腺占位性病变患者进行前期的超声诊断共发现有72例患者存在良恶性病变，其中有66例为良性病变、6例为恶性病变；80例患者经超声诊断检查后进一步实施手术治疗，在手术病理诊断中发现共有75例患者存在良恶性病变，其中良性病变68例、恶性病变7例。即超声诊断甲状腺占位性病变在良性病变中有2例漏诊、在恶性病变中有1例漏诊。超声诊断甲状腺占位性病变的临床准确率为96%。实验结果比较差异明显，（P＜0.05），具备统计学意义。

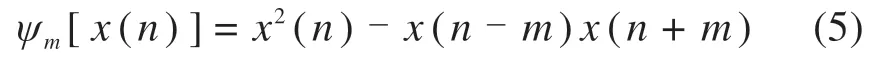
其中：m为多分辨率参数。

定义微分算子Dm，积分算子Im，复合算子Δm的表达式分别为：

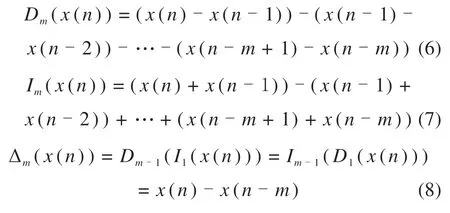
联合公式(1)，算子Ψm可变换为：

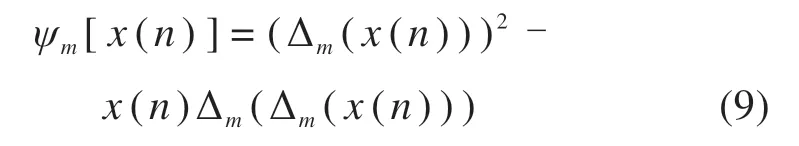
Ψm为Ψ的广义形式，其中：

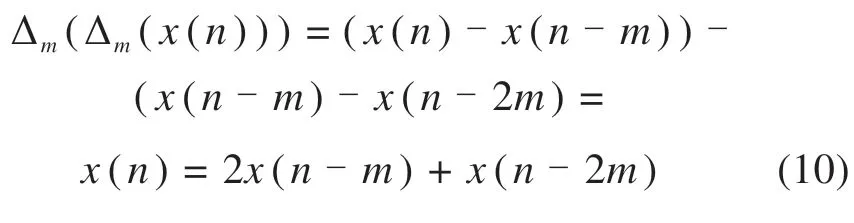
式(5)可通过式(9)获得，由此可知，复合算子包含微分算子和积分算子，即MTEO不仅具备TEO的优势，还能通过改变这2个原创算子的方式进一步抑制噪声，提高信噪比。

另一个影响滤波性能的因素是平滑窗口，当使用MTEO作为增强冲击的工具时，仅需知晓该时刻的3个采样点即可，然而一个突出的噪声点可诱导一个峰值干扰故障冲击点。在处理低信噪比信号时，该噪声将被平滑窗口消除，由此影响后续诊断的准确性。本文选择4m+1长度的汉明窗作为平滑窗口以提取更为纯净的故障脉冲。同时通过调整MTEO的参数以加深故障冲击频率的敏感性。

2 数据分析

2.1 仿真数据分析

当轴承的内圈、外圈和滚动体等元器件表面出现缺陷时，缺陷部位会与其他轴承元件表面接触并发生碰撞，产生周期性冲击成分，该成分在振动信号中将以周期性脉冲的形式出现。根据以上原理，构造出轴承外圈故障仿真数据，图1(a)为该仿真信号的时域波形图，已知采样频率为12 kHz，外圈故障频率为100 Hz。从图1可看出，仿真信号中存在明显的循环性冲击脉冲，但是由于添入的高斯噪声干扰，很大一部分循环脉冲被掩盖，难以发现具体冲击位置。

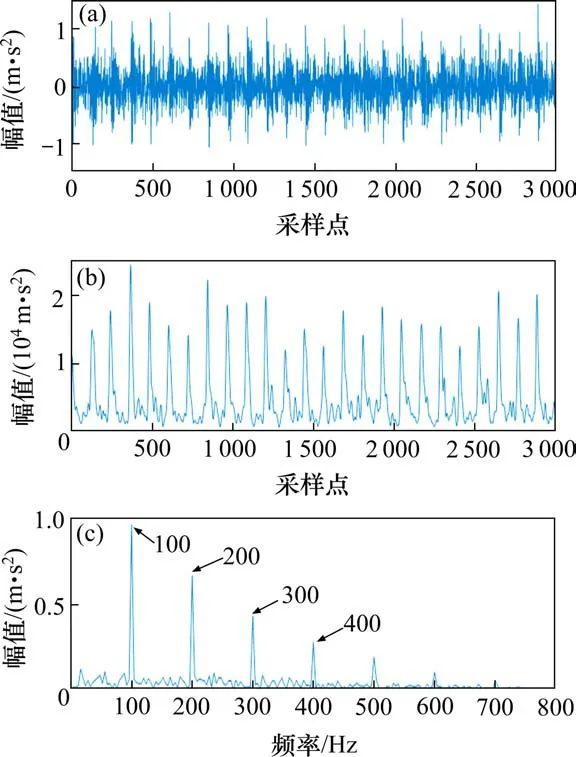
图1 仿真数据MTEO处理结果Fig.1 Results on simulated signals using MTEO

设置多分辨率参数m=4，以长度为4m+1的汉明窗作为平滑窗口对仿真信号进行处理，以此追踪图1(a)的信号总能量，获得图1(b)所示能量谱。从能量谱中可以看出，仿真信号中存在异常冲击的部分能量值较大，而噪声部分能量值较小，且通过能量值的方式，图1(a)中隐藏于噪声中的脉冲点得到了极其有效的凸显，噪声部分则获得极大的压制，信噪分离效果相当优异。图1(b)的包络谱图1(c)中也能得到明显的谱峰成分，其数值与故障频率的基频和倍频成分一一对应。可判别该数据存在严重外圈故障。

进一步加大高斯噪声的影响，图2(a)为包含高噪声分量的低信噪比信号的时域波形图。相对于图1(a)来说，其噪声分量的能量十分强大，已经基本将周期性脉冲完全掩盖，致使特征提取的难度大大提升。为了方便比对，以TEO方法和MTEO方法分别对图2(a)进行处理，获得该信号的TEO能量谱和MTEO能量谱如图2(b)和图2(c)所示。从中可发现，信号经过TEO处理后，能量值虽然得到提升，隐约可见周期脉冲成分，但是噪声分量的消除效果并不理想，干扰影响仍然十分严重，周期脉冲成分依旧存在难以提取的现象。而MTEO处理后噪声分量的消除效果明显，周期脉冲成分突出效果良好，对于故障特征的提取效果明显优于TEO。图2(d)TEO包络谱的1～2倍频成分的谱峰突出，而在3倍频以后的谱峰周围干扰频率较大，严重影响了倍频成分的提取。MTEO包络谱则可轻易提取出1～5倍频成分，且谱峰突出，周围的干扰频率极小。可见MTEO对于周期性脉冲的特征提取和诊断效果优于TEO。

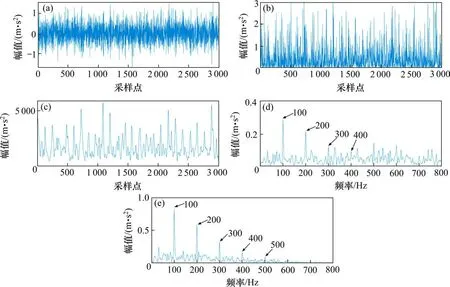
图2 低信噪比数据TEO和MTEO处理结果对比Fig.2 Comparison of processing results between TEO and MTEO for low SNR

2.2 实验数据分析

为了进一步验证所提方法在轴承故障检测中的有效性，本节采用美国Case Western Reserve University轴承数据中心的轴承故障数据进行说明[12-13]。如图3所示，实验平台由三相感应电机(左)、扭矩传感器/编码器(中)、功率计(右)和电气控制部分(未显示)组成，该实验平台可测试2种型号的轴承，分别为安置于驱动端的SKF 6205轴承和安置于风扇端的SKF 6203轴承。采用电火花加工技术在测试轴承上施加不同尺寸(直径分别为0.178，0.356和0.533 mm)的单点故障，并通过安置于底座、驱动端及风机端的加速度传感器实现对轴承状态的监测。

图3 滚动轴承故障模拟实验台Fig.3 Simulation test-bed of rolling bearing failure

选择位于驱动端的加速度传感器采集的外圈故障直径为0.178 mm的驱动端故障轴承数据进行分析。已知实验时主轴转速1 797 r/min，采样频率12 kHz，SKF 6205轴承参数：节径39.04 mm，滚动体直径7.94 mm，滚子数9，接触角0°，结合以上参数可计算得到外圈故障特征频率理论值为107.36 Hz。图4(a)为该数据的时域波形图，可以看到，时域波形图中存在较为明显的周期性冲击特征，但是由于施加的单点故障直径较小，导致故障冲击特征的能量较为微弱，致使表征着故障信息的周期性冲击成分被噪声掩盖，极大一部分故障冲击的位置无法确定。分别采用传统的TEO方法和MTEO方法(设置多分辨率参数m=3)追踪信号总能量后获得图4(a)的能量谱如图4(b)和图4(c)所示。能量谱中可明显看出，处于图4(a)中被噪声淹没的故障冲击特征能量值在图4(b)和图4(c)均得到了显著提升，噪声成分被大幅削弱，冲击位置得以清晰判别。然而MTEO能量谱对于信号的噪声消除效果和故障冲击的凸显效果明显优于TEO。两者的包络谱图4(d)和图4(e)的显示效果接近，包络谱中谱峰突出、具备明显的周期性，且地毯噪声极小，故障频率基频108.1 Hz和轴承故障特征频率理论值107.36 Hz接近，倍频成分亦一一对应，均能得出该数据存在严重外圈故障的结论，与实际情况相符。

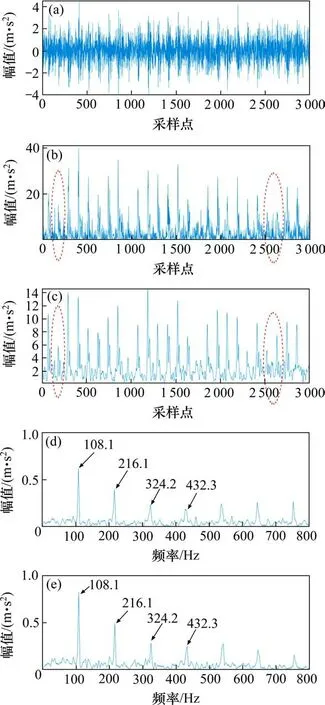
图4 实验室数据处理结果对比(0.178 mm)Fig.4 Comparison of processing results on experimental signals(0.178 mm)

同理，为了对比高信噪比信号的故障特征提取效果，选取位于驱动端的加速度传感器采集的外圈故障直径为0.356 mm和0.533 mm的驱动端故障轴承数据进一步分析，两者信号的处理结果分别如图5和图6所示。由于故障直径尺寸较大，采样获得的原始信号图5(a)和图6(a)中呈现出高信噪比特征，其中的周期性故障冲击特征突出明显，噪声成分的干扰效果较弱。TEO和MTEO在追踪信号瞬时总能量后，获得的能量谱均能够在信号能量的角度大幅度地消除信号中的噪声成分，将故障点周边的干扰噪声进一步压制，使得故障冲击点的提取更加明确。但是相对而言MTEO能量谱的噪声压制效果更好，故障冲击点的凸显效果略优于TEO。由此可见，在处理高信噪比信号时，MTEO和TEO均能较好地取出故障特征，但是在处理低信噪比信号时，MTEO方法寻找故障特征信息的效果更加优异。

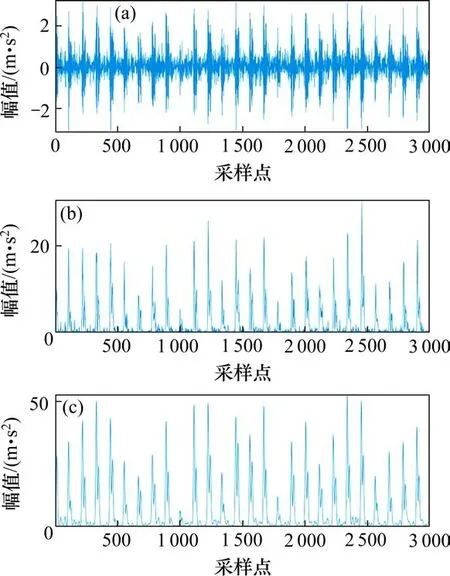
图5 实验室数据特征提取效果对比(0.356 mm)Fig.5 Comparison of feature extraction effect on experimental signals(0.356 mm)

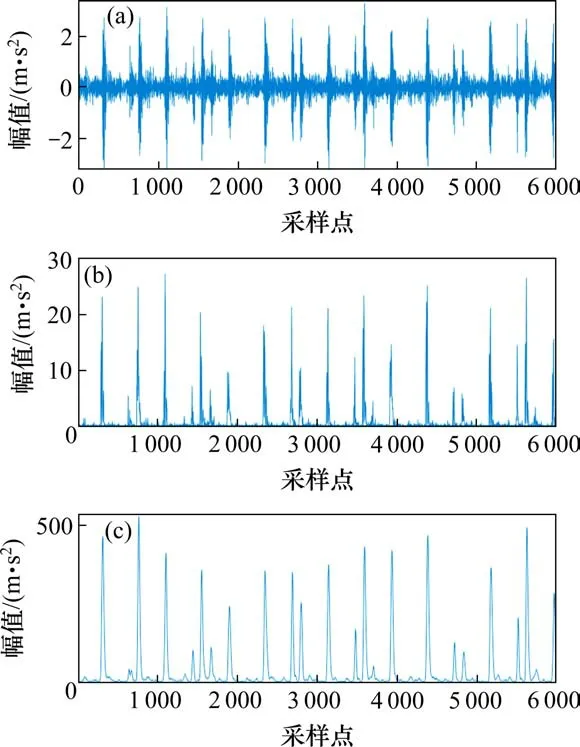
图6 实验室数据特征提取效果对比(0.533 mm)Fig.6 Comparison of feature extraction effect on experimental signals(0.533 mm)

2.3 工程数据分析

数据来源于铁路局机务段轴承检测车间，搜集了机车运行时或大修后的各类异常轮对轴承，机车轴承动态诊断台和外圈故障轴承如图7所示。已知该轴承为NJ2232WB，设置采样频率20 kHz，主轴转速506 r/min，轴承的外圈故障频率为60.12 Hz。

图7 (a)机车轴承动态诊断台；(b)外圈故障轴承Fig.7(a)Dynamic diagnostic table of locomotive bearing;(b)Locomotive bearing with outer ring fault

以振动传感器采样获得的原始振动信号如图8(a)所示，由于轴承故障程度不深，且缺乏较大的负载，图8(a)中的故障脉冲虽然得到一定程度的体现，但是仍然存在如2 000～4 000数据点处故障脉冲被噪声淹没的现象，时域波形图中几乎无法辨别故障冲击点。经过MTEO处理后(多分辨率参数m=7)，图8(a)中一部分干扰脉冲得到了很大的压制，被淹没的故障脉冲尤其2 000～4 000数据点处的突出效果获得了显著增强。包络谱中的谱峰突出，数值和外圈故障频率基频及倍频理论值相对应。由此可表明MTEO拥有极强的抗干扰性，对于挖掘强噪声干扰下的故障信息有一定的优势。

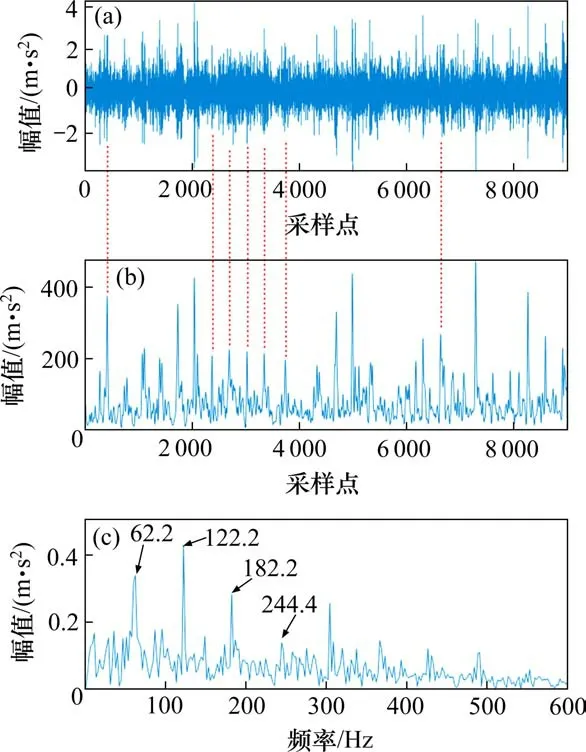
图8 机车轴承信号MTEO处理结果Fig.8 Results on vibration signals of locomotive bearing using MTEO

3 结论

1)MTEO直接计算信号的能量，以此增强隐藏于信号中的故障信息的凸显效果，相比较传统的带通滤波，避免了其局限性。

2)MTEO可通过改变复微分算子和积分算子这2个原创算子的方式在TEO的基础上进一步抑制噪声，提高信噪比，避免TEO处理时出现的负值现象。

3)通过和TEO方案对比，发现MTEO对于故障信息的挖掘能力明显优于传统的TEO方法，具备更加优异的故障诊断效果。