基于旗鱼优化器的列车通信网络拓扑优化研究

班玉友，贺德强,2，陈彦君,2，孙大亮，向伟彬

(1.广西大学 机械工程学院，广西 南宁 530004；2.广西制造系统与先进制造技术重点实验室，广西 南宁 530004；3.南宁轨道交通集团有限责任公司，广西 南宁 530029）

随着通信技术与大数据的深入融合，列车通信网络面临大容量管理信息和控制信息的冲击，新型智能网络设备在列车的应用范围逐渐扩大，列车中传输的大容量数据信息将引起网络拥塞和网络时延上升[1-2]。列车通信网络拓扑作为数据传输的媒介，网络拓扑结构设计的合理性直接影响列车网络的性能，因此，设计适宜的列车通信网络拓扑结构至关重要。在网络性能优化方面，可以通过优化交换节点的网络调度策略来降低网络时延[3-4]，但仅从网络的局部角度去改善网络性能难以保证其性能全面提升，故通过设计网络拓扑的优化策略进行网络性能优化已经成为研究者关注的热点问题之一。在众多网络拓扑优化过程中，所涉及的拓扑优化指标主要包括网络时延、网络健壮性、流量负载及拓扑成本等[5-7]。WANG[8]提出一种基于循环图来解决现代集成交换网络系统的带宽效率、容错性和交换负载平衡问题的拓扑优化算法，但未考虑网络中各交换设备集成后对网络时延的影响。LIU等[9]基于图论建立一种可用于优化设计叉式电动牵引车CAN通信网络系统的数学模型，但对于通信网络系统的通信效果的衡量，仅考虑了总线负载率而未考虑网络延迟。HANAY等[10]提出一种基于机器学习来评估网络拓扑优化指标的方法，该研究验证了网络时延是较好的拓扑优化指标，上述研究考虑了网络负载因素，却忽略了网络时延指标的影响。KHAN等[11]建立一种用于求取最佳分布式局域网络拓扑结构的模糊目标编码模型，但该研究考虑较多的优化指标难以保证各因素权重的公平性。田寅等[12]提出一种优化设计列车通信网络拓扑的双层规划模型，其综合了时延、可靠性与成本指标，但未对网络时延进行定量研究。上述研究对特定网络拓扑进行优化时，未同时考虑网络负载和网络时延对网络拓扑优化性能的影响，且缺乏时延的量化分析，为实现网络信息的快速交换和资源的实时共享，本文综合考虑网络时延、网络负载与拓扑成本对列车通信网络性能的影响，构建在成本约束下满足负载均衡与低时延的网络拓扑结构优化模型。旗鱼优化器(Sailfish Optimizer，SFO)是一种新型元启发式优化算法，主要启发于旗鱼群狩猎的攻击交替策略，具有搜索能力强、寻优速度快的特点[13]，并且已经用于求解码头泊位分配问题[14]，取得了一定成效。因此，本文提出基于旗鱼优化器的网络拓扑优化算法来改善列车通信网络性能，最后使用MATLAB建模分析和OPNET仿真分析来验证本文研究方法的可行性。

1 网络拓扑设计问题描述

1.1 网络拓扑优化问题

列车通信拓扑结构主要由列车级、车辆级网络组成，本文选取连接各个车辆的列车级网络拓扑作为研究对象，主要从网络时延、网络负载和网络拓扑成本3个方面对列车通信网络拓扑结构进行优化设计。考虑网络拓扑优化是根据给定的条件对网络中的网络设备重新规划空间位置和改变设备之间连接状态的一种优化方法，设定模型假设为：1)网络拓扑中交换节点的处理能力和网络链路带宽满足工作要求；2)网络拓扑中不存在孤立的链路和网络设备，即满足0.5·|Nd|·|Nd-1|≥|Ll|≥|Nd|-1，|Ll|与|Nd|(|Nd|=2,3,4,…)分别为网络拓扑中链路和网络节点的数量；3)网络拓扑中交换节点的端口数量满足工作需求，并且具有足够端口余量。

1.2 目标函数的确定

采用无向图G=(N,E)描述各网络设备之间的连接状态，其中Nd={n1,n2,…,nm}为无向图中节点的集合，E=(e1,e2,…,ek)为无向图中边的集合。关于节点之间的连接状态，当2个节点相连时，rij=1，否则rij=0，具体描述为：

关于网络设备之间的通信状况，定义反映设备间通信关系的通信矩阵C为：

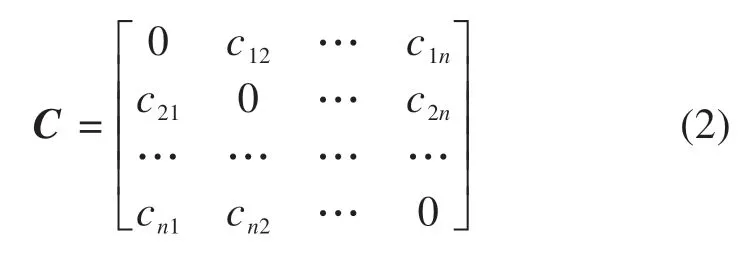
其中：元素cij为2个设备之间通信流量的权值，通过[0,10]内的整数值进行权值描述。反映节点之间连接关系的邻接矩阵Rl映射为：

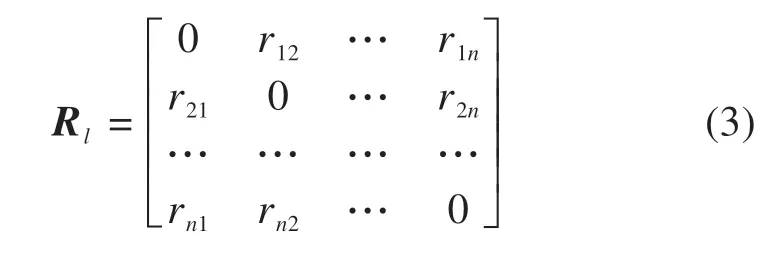
关于列车通信网络时延指标的衡量，本文引入网络演算理论进行时延计算分析，该理论是一种基于最小加代数的网络性能分析方法[15]，可用于分析网络流量较坏状况下的端到端时延上界，通过广义增函数γv,b(t)=v·t+b表征数据流的到达曲线，其中v表示数据帧平均生成速率，b表示最大 突 发 传 输 量。βV,T(t)=V[t-Ts]+=max{0,V(t-Ts)}表征数据流速率延迟服务曲线，其中V表示服务速率，Ts为最大延迟。车载交换机的总服务曲线定义为β(t)=V s[t-0]+，V s为车载以太网交换机总服务能力，其值与网络带宽C0相等。则列车通信网络交换机系统提供的速率延迟服务曲线βsum(t)为：

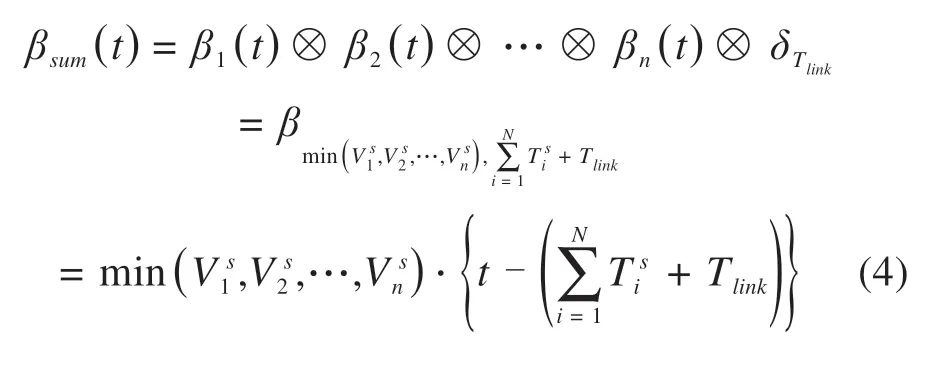
式中：βi(i=1,2,3,…)为每个列车级交换机所提供的服务曲线；V is(i=1,2,3,…)为以太网交换机的服务能力；δTlink为网络链路固定时延的服务曲线；(i=1,2,3,…)为交换机内的传输时延。从网络拓扑优化角度分析，将各个数据帧在交换节点内的传输时延设为相等的固定时延Tss，则有数据帧在N个车载交换机和相应网络链路中传输和传播的最坏时延T(X)为：

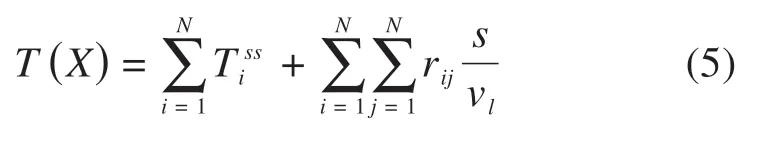
式中：s为网络设备之间的链路长度；vl为数据帧在链路中的传输速率；rij为式(1)中反映设备间连接关系的状态值。

在给定的通信任务下，网络中的通信流量仍会出现负载不均衡现象，因此，需要对列车通信网络的负载指标进行衡量，则列车车厢k的通信负载Lk表示为：

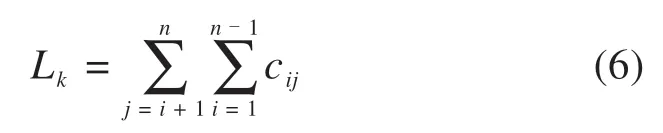
式中：cij为网络设备之间的通信流量。则有列车级网络的通信负载U(k)和通信负载均值：

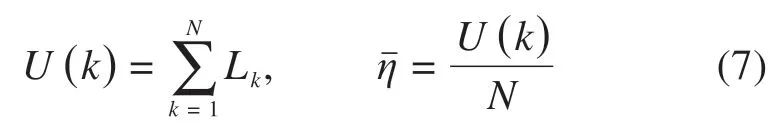
式中：N为列车级网络中交换节点个数。为对网络负载指标进行有效衡量，将列车车厢的通信网络负载方差Dk表示为：

通过进一步分析得出列车级网络负载的方差D(X)：

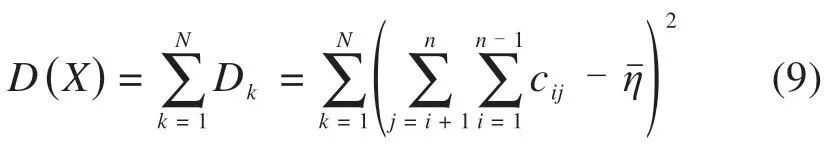
关于网络拓扑的成本指标，本文主要考虑网络链路和交换节点的成本，则网络拓扑的成本指标C(X)为：

式中：c(rij)为网络链路的单位成本；c(dk)为交换节点设备的单位成本；dk表征交换节点设备；sij为2个设备之间的链路长度；rij表示2个设备之间的链路连接状态。

在列车级网络拓扑优化中，本文考虑将负载方差和时延指标作为优化目标，并根据实际工程需求引入权重参数ε*来权衡网络负载和时延。对于成本指标的衡量，将其设置为网络拓扑优化过程中的约束条件，为了简化拓扑优化过程，利用罚函数法将有约束的优化问题转换为带罚函数q(X)的无约束优化问题进行求解分析，则带罚函数的目标函数F(X,ε*,θ)为：

式中：θ为惩罚因子，θ> 0；θ·q(X)为惩罚项；Cmax为列车级网络拓扑的最大成本指标。式(12)反映前述的邻接矩阵具有对称性；式(13)表示网络拓扑中不存在孤立的节点设备；式(14)保证了交换节点的端口具有余量，Pi为交换节点的端口数量；式(15)和式(16)保证了数据帧仅从任意节点输入或输出1次。

2 网络拓扑结构优化策略

2.1 拓扑优化方法

列车通信网络的拓扑优化算法实际上是在给定的约束条件下，生成网络拓扑对应的最优邻接矩阵，考虑本文的优化目标为网络负载均衡性和网络时延，其中涉及较多节点之间网络通信流量的演算，为能在有效时间内对研究问题进行求解，利用基于旗鱼优化器的列车通信网络拓扑优化算法进行拓扑优化操作。

2.2 网络拓扑优化算法设计

本文研究模型为多目标优化问题。为更好地求解问题模型，通过权重和法将多目标转换为具有单一优化目标的聚合目标函数[16]，并基于旗鱼优化器的算法来求解聚合目标函数。列车通信网络拓扑优化的算法流程图如图1所示。

图1 网络拓扑优化算法流程图Fig.1 Network topology optimization algorithm flowchart

基于旗鱼优化器的列车通信网络拓扑优化寻优过程的关键步骤可表示为：

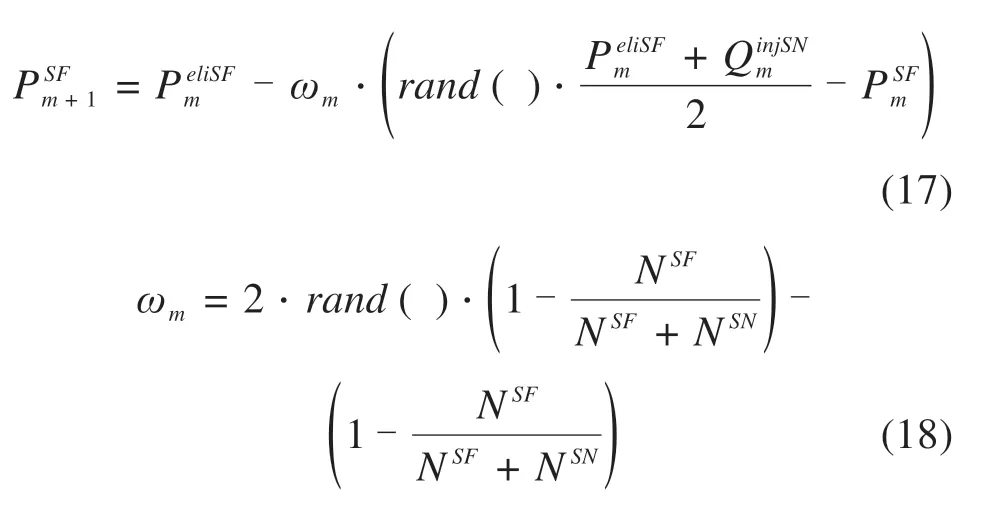
式(17)描述了旗鱼在第m+1代时位置更新的主要操作，在第m次迭代时，为旗鱼的当前位置，为旗鱼的最佳位置，并将受伤的沙丁鱼位置作为沙丁鱼的最佳适应度值，rand()为0～1之间的随机数。式(18)描述了与猎物群密度相关的系数ωm，NSF和NSN分别表示旗鱼和沙丁鱼的数量，其参数值最初由给定的种群数量和旗鱼所占比例决定，随着算法迭代运行，旗鱼群体捕猎时猎物数量会减少，上述2个参数值的变化会对旗鱼的位置更新操作产生影响，进而影响最佳负载方差指标和最佳时延指标的求解精度和网络拓扑优化算法的收敛情况。沙丁鱼在每次迭代中均有位置更新，则第m+1代时的沙丁鱼位置为：

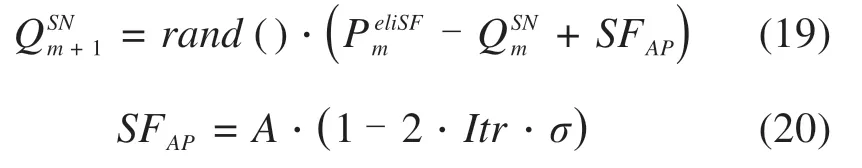
式(19)中：为第m次迭代时的沙丁鱼位置，SFAP为第Itr代时旗鱼的攻击能力，由参数A和σ控制攻击能力的变化，当攻击力SFAP>0.5时，通过式(19)更新所有沙丁鱼位置，否则由α=NSN·SFAP和β=γ·SFAP分别确定需要更新的沙丁鱼数量和维度数量，其中γ为变量的数量。进而综合考虑旗鱼和沙丁鱼的位置，获取最优解以生成反映拓扑结构连接关系的邻接矩阵。

关于拓扑优化设计操作，由于旗鱼优化器通常用于求解最小值优化问题，故将带罚函数的目标函数F(X,ε*,θ)作为适应度函数，以获取均衡最佳负载方差和最佳网络时延指标下的网络拓扑。具体操作表现为随机初始化种群后，计算初始适应度值，进而根据式(17)～(20)分别对旗鱼和沙丁鱼的位置进行更新，通过对比计算所有适应度值后获取全局最优位置，最后得出相应的邻接矩阵元素值。考虑邻接矩阵具有对称性，为简化算法计算的复杂度，采用邻接矩阵的上三角元素进行研究分析，则有编码方式rl为

3 案例分析

为验证本文设计的列车通信网络拓扑优化算法的可行性，在给定通信流量矩阵的基础上，设计实验案例对列车级网络拓扑结构进行优化，并采用OPNET Modeler仿真平台进行建模仿真分析。

3.1 列车网络拓扑优化

关于列车级网络拓扑优化，本文在每节车厢各选取5个终端设备作为车厢之间数据传输的节点，选取中央控制单元(Central Control Unit，CCU)、牵 引 控 制 单 元(Traction Control Unit，TCU)、列车自动控制(Automatic Train Control，ATC)、制动控制单元(Brake Control Unit，BCU)和智能显示单元(Intelligent Display Unit，IDU)作为头车与尾车数据帧传输的接收发端，车辆控制单元(Vehicle Control Unit，VCU)、车门电子控制单元(Electronic Door Control Unit，EDCU)、辅 助 控 制单元(Auxiliary Control Unit，ACU)、远程输入输出模块(Remote Input/Output Module，RIOM)和协议转换单元(Protocol Conversion Unit，PCU)作为中间车厢的数据帧传输的接收发端。根据车辆车载控制网络数据传送规范及相应网络设备之间的传输规律，利用通信流量矩阵来描述各个车厢网络设备之间的通信流量，为简化分析，选用[0,10]内的整数值对网络设备之间的通信流量进行权值描述，如图2所示。

图2 通信流量矩阵Fig.2 Communication flow matrix

本文对8节动车组的列车级网络拓扑进行优化研究，每节车厢具有1个交换节点，考虑链路的布线方式，设车厢内的链路长度为50 m，相邻2个车厢之间的链路长度为75 m。为降低计算的复杂度，设置网络链路为每米0.5个单位成本，列车级交换节点为50个单位成本。在图2给定的通信流量矩阵基础上，本文采用基于旗鱼优化器的网络拓扑优化算法进行拓扑优化，仿真参数设置为A=4，σ=0.001，最大迭代次数和初始种群分别为500和100，旗鱼所占比例为0.3，根据多次试验研究和经验取权重因子ε*=0.999，保证求解时网络负载均衡度和网络时延处于同一数量级，并在相同的最大迭代次数和初始种群下采用粒子群算法(Particle Swarm Optimization，PSO)对列车通信网络拓扑进行对比优化来体现本文网络拓扑优化算法的优势。

通过MATLAB仿真，列车级网络拓扑优化进程的结果如图3所示，反映了网络拓扑优化过程中目标函数适应度值和优化算法迭代次数的关系，随着算法迭代次数的增加，目标函数的适应度值逐渐达到最佳。应用粒子群算法时，在第337代迭代时适应度值收敛到全局最优；采用本文研究的网络拓扑优化算法时，在第92代迭代时适应度值收敛到全局最优，并且采用不同优化算法优化后的值均为1.157 47，相比应用粒子群算法优化问题模型，基于旗鱼优化器的列车通信网络拓扑优化算法表现出较好的收敛效果，收敛速度更快，寻优能力更强。根据优化出的最优解所生成的邻接矩阵，获得该矩阵对应的列车级网络拓扑结构，如图4所示，优化生成的网络拓扑表现出较好的冗余性。进一步分析得出优化后网络拓扑的负载方差和网络时延，并与总线型网络拓扑的相应网络指标进行比较分析，如表1所示，相比总线型拓扑，优化后网络拓扑的负载方差和网络时延分别降低了43%和24%，负载均值有一定程度的降低，经济性有所增加，但该指标值仍在工程实际允许范围之内。

图3 列车网络拓扑优化算法进程Fig.3 Train network topology optimization algorithm process

图4 列车级网络拓扑Fig.4 Train-level network topology

表1 优化结果分析Table 1 Analysis of optimization results

3.2 列车通信网络仿真

为进一步对本文研究方法加以验证，利用OPNET仿真软件进行建模分析，在3.1节优化出的列车级网络拓扑结构基础上，将车辆级网络拓扑设计为星型结构，每个车辆级交换机配置20个终端设备(End Device，ED)，因此，列车通信网络拓扑仿真模型如图5所示。仿真场景配置为300 m×150 m，网络带宽C0为100 Mbps。为体现优化后列车网络拓扑的优越性，具体操作表现为在配置相同的通信数据的基础上，将优化后的列车级网络拓扑与常见的总线型列车级网络拓扑进行对比分析，仿真结果及其分析如下。

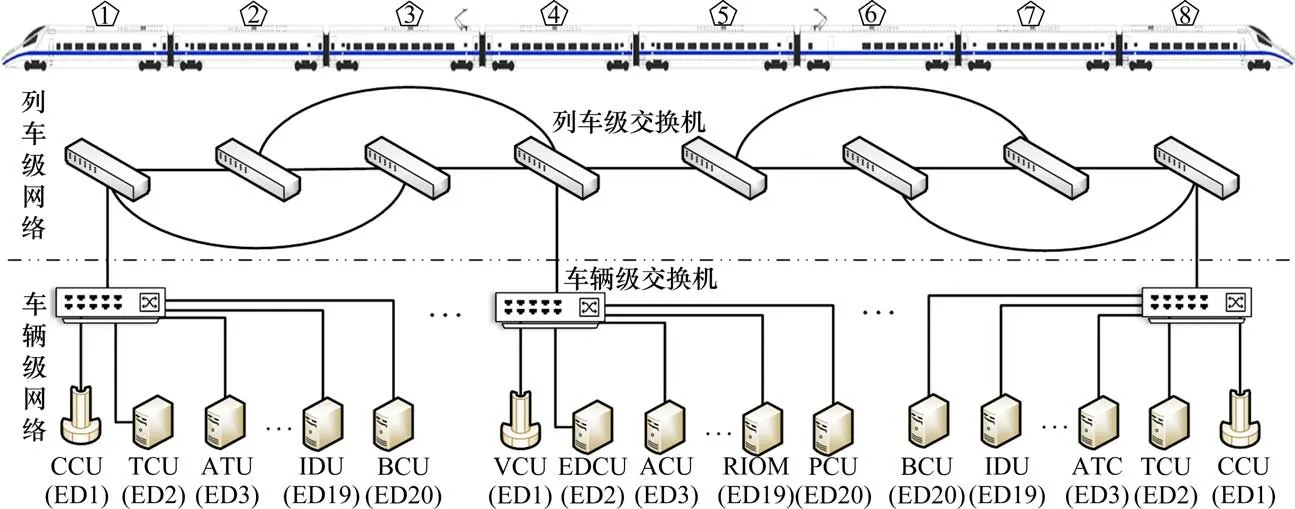
图5 列车通信网络拓扑模型Fig.5 Train communication network topology model

对不同列车级网络拓扑的列车通信网络吞吐量进行考察，如图6所示，分别描述了优化后的列车级网络拓扑和总线型列车级网络拓扑的网络吞吐量，列车通信网络吞吐量稳定后的均值分别为5.45 Mbps和4.27 Mbps，相比总线型列车级网络拓扑，优化后的网络拓扑表现出较好的网络性能，列车通信网络状况更好。

图6 列车通信网络吞吐量Fig.6 Train communication network throughput

在考察列车通信网络吞吐量的基础上，对列车通信网络端到端时延进行研究分析，仿真结果如图7所示，列车级网络拓扑为总线型时，列车通信网络端到端时延为0.561 ms，采用基于旗鱼优化器的拓扑优化算法对列车级网络拓扑进行优化后，列车通信网络端到端时延为0.474 ms。相比总线型列车级网络的端到端时延，优化后的列车级网络端到端时延降低了15.5%，符合3.1节的优化研究规律。有效地改善了列车通信网络性能，并且经仿真分析得出的网络时延符合列车通信网络标准。

图7 列车通信网络端到端时延Fig.7 Train communication network end-to-end delay

4 结论

1)考虑列车通信网络拓扑成本等因素与模型的约束关系，建立了以网络负载均衡和网络时延最低为目标的列车通信网络拓扑优化模型。设计基于旗鱼优化器的列车通信网络拓扑优化算法，解决了列车通信网络负载不均衡、时延高的问题，确保列车通信网络较高的服务质量。

2)通过MATLAB建模仿真分析，与总线型列车级网络相比，优化后的列车级网络拓扑的负载方差和网络时延分别降低了43%和24%，有效改善了列车通信网络性能，能够为网络拓扑优化工作提供理论参考。

3)根据网络仿真分析，相比于总线型列车级网络，优化后的列车网络吞吐量展现了较好的网络传输效率，相应的网络端到端时延降低了15.5%，网络性能得到一定程度的提升，验证了本文研究方法的可行性。在将来的网络拓扑优化工作中，考虑更多目标约束对车辆级网络拓扑优化是有待扩展的研究内容。