基于交互信息的混合特征选择算法

姜文煊，段友祥，孙歧峰

中国石油大学(华东)计算机科学与技术学院，山东青岛266580

油气地质评价是利用特定的评价方法对评价对象的含油气性或含油气概率进行综合评判，然后根据综合评判值对评价对象进行分类评价[1]，并已成为油气勘探决策分析中一项必不可少的工作，且在减少勘探开发风险以及提高油气生产经济效益等方面具有非常重要的现实意义。在油气地质评价过程中，单一属性往往很难全面反映地质特征，于是需要选出多个属性。在这些属性中，各个属性对评价结果的影响程度各不相同，其中有些关键属性对评价结果的影响较大。因此，在实际应用中如何筛选出合理而有效的地质属性是至关重要的。特征选择能在不失去数据原有价值的基础上去除冗余特征，提高数据的质量[2]；近年来又在获得关键属性的应用方面表现出较好的性能而受到研究人员的广泛关注[3]。

根据不同的选择策略，特征选择方法通常分为过滤法、封装法和嵌入法[4]。过滤法[5-7]是以独立的评估函数来评估特征子集而实现特征选择的，既不会偏向任何分类器，又不必直接优化任何特定分类器的性能，不但计算效率高，而且不会继承分类器的任何偏差。封装法[8-9]以预定的分类器评估特征子集进行特征选择，将给定学习算法的性能作为标准函数评估所选特征子集的有用性。该方法借助了分类器控制特征子集的选择，虽然在大多数情况下具有比过滤法更好的性能，但是在计算方面更加费时，且容易出现过拟合现象。嵌入法[10-11]将特征选择嵌入分类算法，在模型训练过程中完成特征选择。这种方法介于过滤法和封装法之间，具有高效且能与学习算法进行交互的优点，但仅适用于某些特定的分类算法。综上所述，3种方法各有利弊。为了快速获得高精度的输入特征，研究人员提出了将两种或多种特征选择方法相结合作为一种混合特征的选择方法，取得了很好的效果[12]。

基于互信息的特征选择方法不但能够捕获变量之间的非线性关系而且适用于复杂的分类问题，因此受到了广泛关注。传统的基于互信息的特征选择方法，如最大相关最小冗余（minimal redundancy maximal relevance,mRMR）[13]、条件互信息最大化（conditional mutual information maximization,CMIM）准则[14]、双输入对称关联（double input symmetrical relevance,DISR）[15]、联合互信息（joint mutual information,JMI）[16]等都是通过去除不相关、冗余的特征，来选择与目标类别相关性最大且所选特征之间的冗余性最少的特征子集。除了识别无关和冗余的特征外，一个重要又常被忽略的问题就是特征间的信息交互[17]。很多单独的特征可能与目标集无关，一旦组合在一起却与目标集高度相关。

鉴于此，本文结合特征的相关性、冗余性以及交互性来衡量特征的重要性，并利用过滤法和封装法的优势提出了一种基于交互信息的混合特征选择（hybrid feature selection based on mutual information,MIHFS）算法。

1 相关工作

1.1 熵、联合熵和条件熵

熵[18]是信息论中用来度量随机变量的不确定性的。数据包含的信息量越多，熵值就越大。设X为离散型随机变量，则X的熵定义为

式中：p(x)表示随机变量X的边缘概率分布函数，且H(X)≥0。

两个离散型随机变量X和Y的联合熵可定义为

式中：p(x,y)表示随机变量X、Y的联合概率分布函数。

条件熵H(Y|X)表示在X已知的条件下Y的不确定性，熵、联合熵和条件熵三者之间的关系为

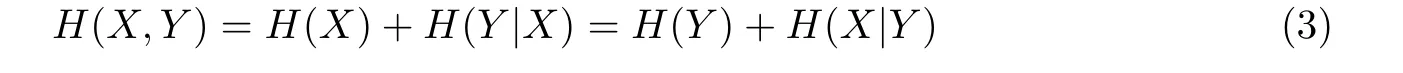
1.2 互信息和对称不确定性

互信息和对称不确定性SU是两种典型的技术，通常用于衡量两个随机变量之间的相关性。假设X和Y是两个离散型随机变量，则X和Y之间的互信息I(X;Y)可定义为

也可表示为

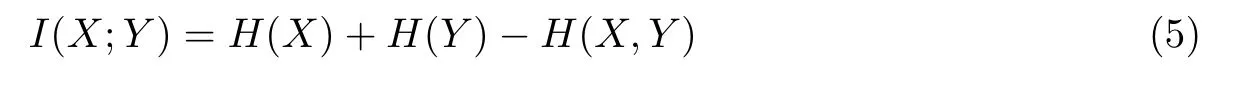
由式（5）可知，当I(X;Y)≥0且其值越大时，X与Y的相关性就越强；当I(X;Y)=0时，X与Y相互独立，此时两者无相关信息。当Y为标签或类属性时，I(X;Y)就称为信息增益，可用于衡量随机变量X提供的有关Y的信息。

联合互信息表示随机变量与目标变量之间的关系。设X、Y、Z是3个离散型随机变量，则它们三者之间的联合互信息I(X,Y;Z)可定义为

也可以表示为

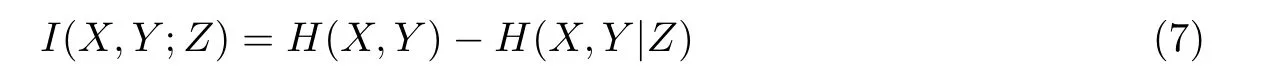
当衡量3个随机变量之间的交互作用时，就用到了交互增益，即交互信息。设X、Y、Z是3个离散型随机变量，其交互增益I(X;Y;Z)可定义为

也可以表示为

当I(X;Y;Z)<0时，随机变量X和Y组合在一起提供的信息小于它们各自提供的信息之和，表明X和Y之间存在信息冗余；当I(X;Y;Z)=0时，随机变量X和Y组合在一起提供的信息等于它们各自提供的信息之和，表明X和Y之间相互独立；当I(X;Y;Z)>0时，随机变量X和Y组合在一起提供的信息大于它们各自提供的信息之和，表明X和Y组合在一起可以提供一些它们分开时所不能提供的信息，两者之间信息互补。

针对互信息偏向于取值较多的特征问题[19]，采用对称不确定性将互信息的范围缩放到[0,1]，也就是将对称不确定性视为归一化的互信息[20]。对称不确定性的定义为

2 MIHFS算法

2.1 算法描述

互信息通常用于衡量特征之间的相关性、冗余性和交互性[21]。基于互信息的特征选择旨在选择与目标类别相关性最大且所选特征之间的冗余性最少的特征。使用互信息作为相关性度量时往往偏向于更多值的特征[19]，为了解决这个问题，根据对称不确定性选出与类别相关性最强的特征，同时筛选出与类别不相干的特征。若数据集D具有完整的特征集F={f1,f2,···,fm}和类标签C，则对称不确定性可以表示为

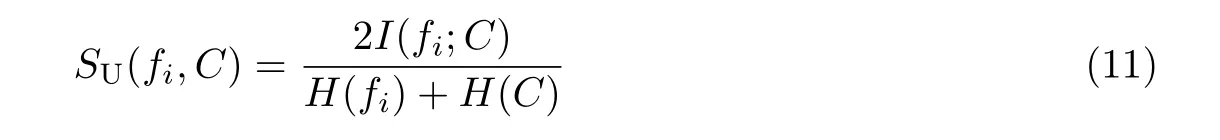
大多数基于互信息的特征选择算法进行特征选择时，通常只考虑去除不相关的和冗余的特征而忽略了特征间的交互作用。为了能更准确地衡量特征的重要性，获得更好的分类性能，本文提出了一种度量标准来衡量特征间的相关性、冗余性以及交互性，该度量标准可以表示为

本文采用顺序前向浮动搜索策略，根据提出的度量标准将各特征进行降序排序，然后将特征依次加入候选特征集，并计算KNN的分类准确率。若KNN的分类准确率提高，则将该特征加入特征子集。

MIHFS算法的描述性伪代码如算法1所示。

MIHFS算法主要包括两部分内容。第1部分初始化所选特征子集和候选特征集，然后计算每个特征和类的对称不确定性，将与类标签相关性最大的特征从特征集中移出后加入候选特征集和特征子集，同时过滤掉与类标签无关的特征，记录在当前候选特征集下KNN的分类准确率。第2部分根据提出的度量标准计算剩下特征的重要性，将最重要的特征从特征集中移出后加入候选特征集，计算在当前候选特征集下KNN的分类准确率。若KNN的分类准确率提高，则将该特征加入特征子集，反之将该特征从候选特征集中移出。重复此过程，直至特征集为空。

2.2 MIHFS算法特点

MIHFS算法具有以下3个特点：

1）采用对称不确定性，解决了以互信息作为相关性度量时偏向于取值较多的特征的问题。

2）提出了一种度量特征重要性的方法，不仅能有效筛选出信息量丰富的特征，而且能去除冗余特征，使得所选特征的分类准确率最高。

3）将过滤法和封装法相结合，可进一步减少冗余特征，使算法能够保留较少数量的特征。

3 实验结果及分析

3.1 数据集描述

为了验证本文提出算法的性能，从UCI(http://archive.ics.uci.edu/ml/index.php)机器学习存储库中选取了8个公共数据集进行测试。这些数据集出自3个不同的领域，涵盖了二分类问题和多分类问题，特征数量从4个到73个不等，样本数量也从150个到1 599个不等，这些公共数据集及地质数据集的相关信息如表1所示。表1中：Iris代表鸢尾花数据集，Cortex_Nuclear代表小鼠蛋白质基因表达数据集，Wine代表葡萄酒数据集，ILPD代表印度肝病数据集，Winequality-Red代表红酒品质数据集，Breast-Cancer-Wisconsin代表威斯康星州乳腺癌数据集，Glass代表玻璃识别数据集，Ionosphere代表电离层数据集，Geological为地质数据集。在以上这些数据集中，Iris、Cortex_Nuclear、Winequality-Red、Breast-Cancer-Wisconsin、Glass、Geological数据集均为真实数据集。

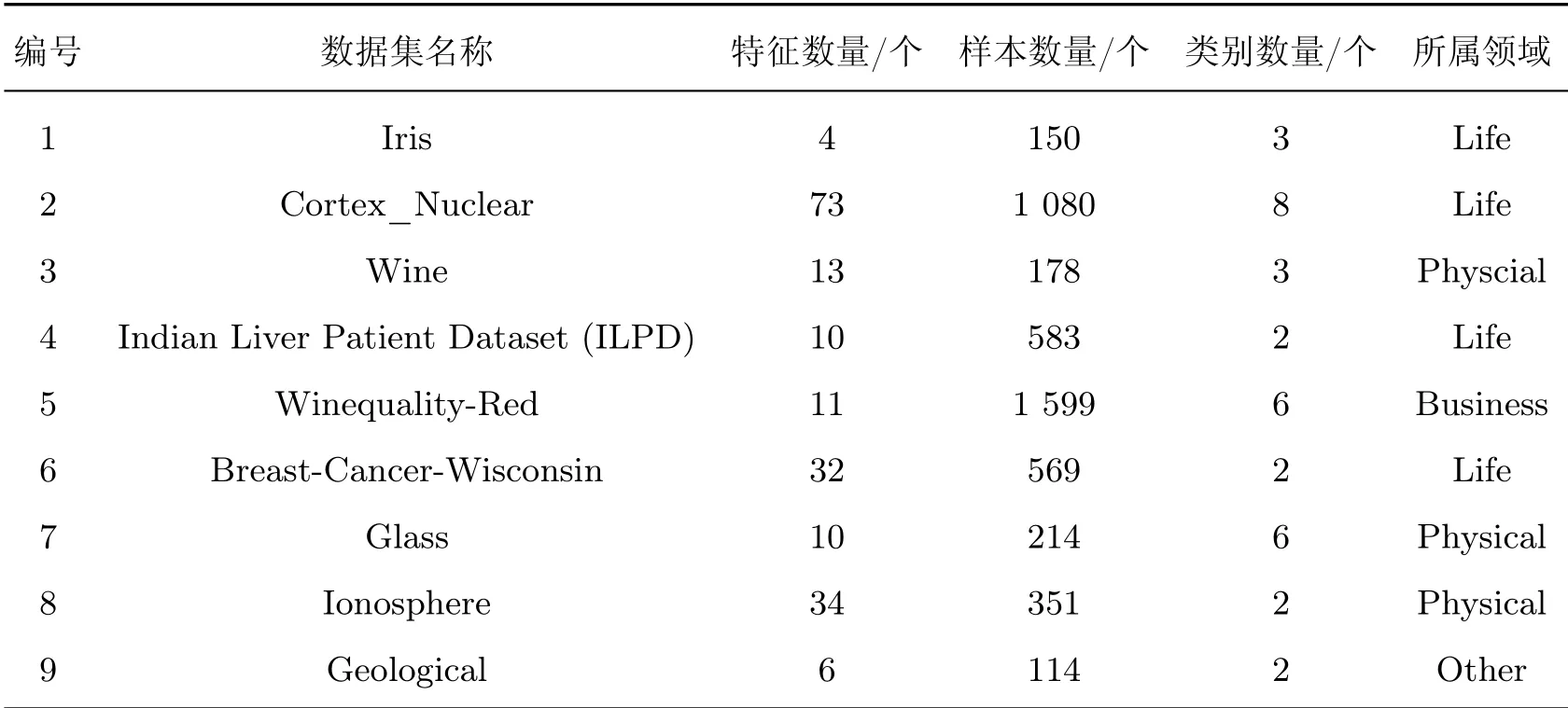
表1 数据集描述Table 1 Data set description

3.2 数据预处理

为了消除不同量纲对评价结果的影响，将原始数据集进行归一化处理统一到[0,1]内，其计算公式为

式中：i=1,2,···,n;j=1,2,···,m。

针对表1数据集的数据缺失问题，以该属性在其他数据上的均值来填充。由于有的数据集包含非数值型的特征，本文将这些特征转化为数值型特征。

3.3 实验及分析

好的特征选择方法不仅可以准确地选出信息量丰富的特征，而且具有较强的稳定性。准确性的含义包含两方面：1）特征选择方法应选择具有更好分类性能的特征；2）应选择尽可能少的特征。

下面从分类准确率、特征子集数量以及算法的稳定性三方面将MIHFS算法与mRMR、JMI、DISR、随机森林（random forest,RF）、REFS（efficient and robust feature selection）[22]、条件相关特征选择（conditional relevance feature selection,CRFS）[23]、IWFS（interaction weight based feature selection）[24]这7种特征选择算法在8个UCI数据集及Geological数据集上进行实验比较。

分类准确率常用作衡量算法分类性能的重要指标，值越高说明算法的分类性能越好。分类准确率的计算公式为

式中：n表示分类正确的样本数量，N表示样本总数。

在不同数据集上，除MIHFS算法以外的各算法选择不同数量特征时所对应的10次迭代结果平均分类准确率的变化情况如图1～4所示。

图1 7种特征选择算法在Iris数据集和Cortex_Nuclear数据集上的平均分类准确率Figure 1 Average classif ication accuracy by seven feature selection algorithms in Iris dataset and Cortex_Nuclear dataset

图2 7种特征选择算法在ILPD数据集和Wine数据集上的平均分类准确率Figure 2 Average classif ication accuracy by seven feature selection algorithms in ILPD dataset and Wine dataset

在不同数据集上，MIHFS算法选择不同数量的特征所对应的10次迭代结果的平均分类准确率的变化情况如图5所示。

图5 7种特征选择算法在Geological数据集上的平均分类准确率Figure 5 Average classif ication accuracy by seven feature selection algorithms in Geological dataset

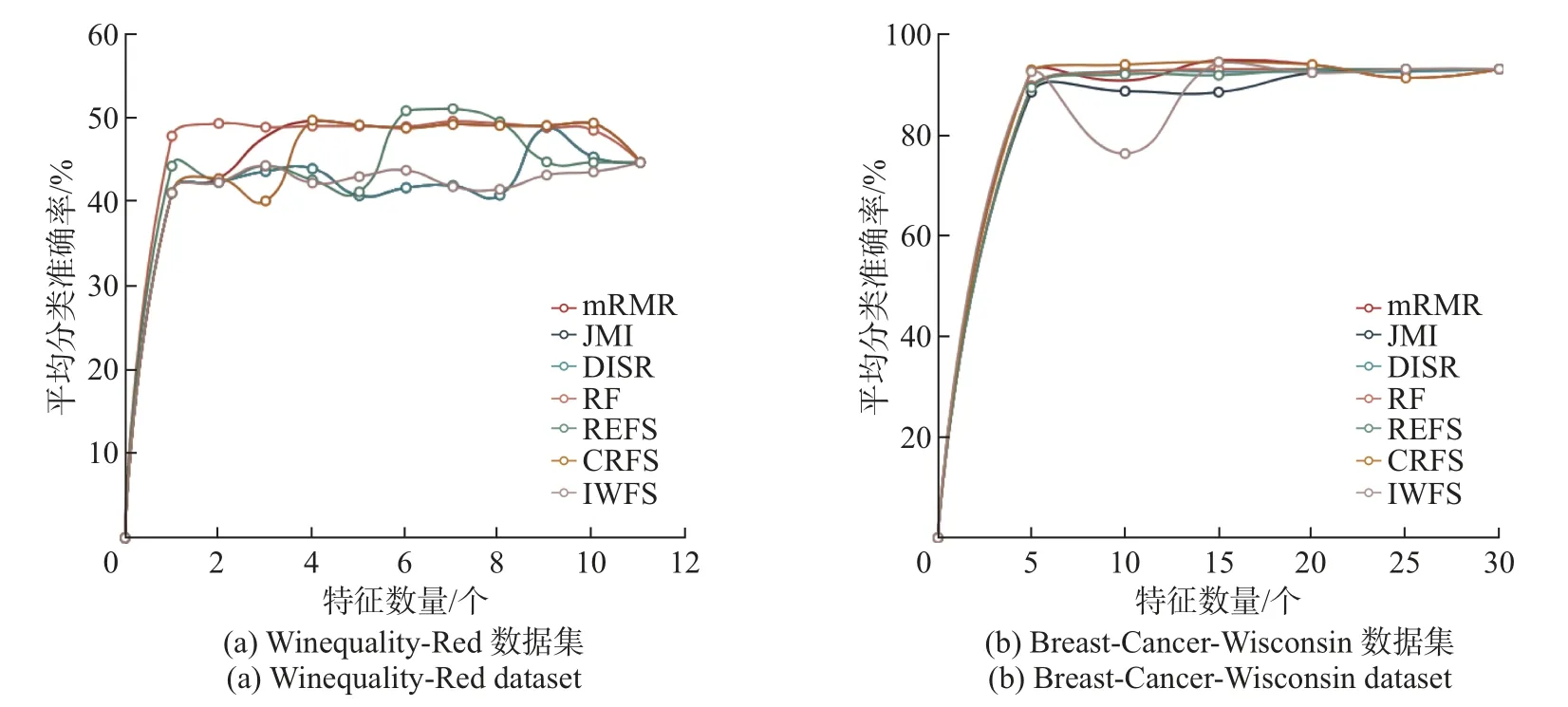
图3 7种特征选择算法在Winequality-Red数据集和Breast-Cancer-Wisconsin数据集上的平均分类准确率Figure 3 Average classif ication accuracy of seven feature selection algorithms in Winequality-Red dataset and Breast-Cancer-Wisconsin dataset

图4 7种特征选择算法在Glass数据集和Ionosphere数据集上的平均分类准确率Figure 4 Average classif ication accuracy by seven feature selection algorithms in Glass dataset and Ionosphere dataset

表2给出了图1～5中mRMR、JMI等7种特征选择算法在不同数据集上分类器的最高平均分类准确率以及MIHFS算法在不同数据集上的分类准确率，表中数据加粗部分表示各算法在各个数据集上达到的最高分类准确率。

从表2中的结果可以看出：本文提出的MIHFS算法与其他特征选择算法相比具有明显的优势，其中MIHFS算法在Iris数据集上比REFS算法的最高分类准确率提高了3.81%，在Wine数据集上比REFS算法的最高分类准确率提高了17.13%，在ILPD数据集上比JMI、DISR以及RF算法的最高分类准确率提高了4.16%，在Winequality-Red数据集上比IWFS算法的最高分类准确率提高了10.57%，在Glass数据集上比REFS算法的最高分类准确率提高了6.89%，在Geological数据集上比REFS算法的最高分类准确率提高了7.15%。MIHFS算法虽然在Ionosphere、Breast-Cancer-Wisconsins数据集上并未取得最好的效果，但是在所有数据集上的分类准确率的均值高于其他7种特征选择算法在分类器上的最高分类准确率的均值。由此可以看出，MIHFS算法所选择的特征具有很好的分类性能。

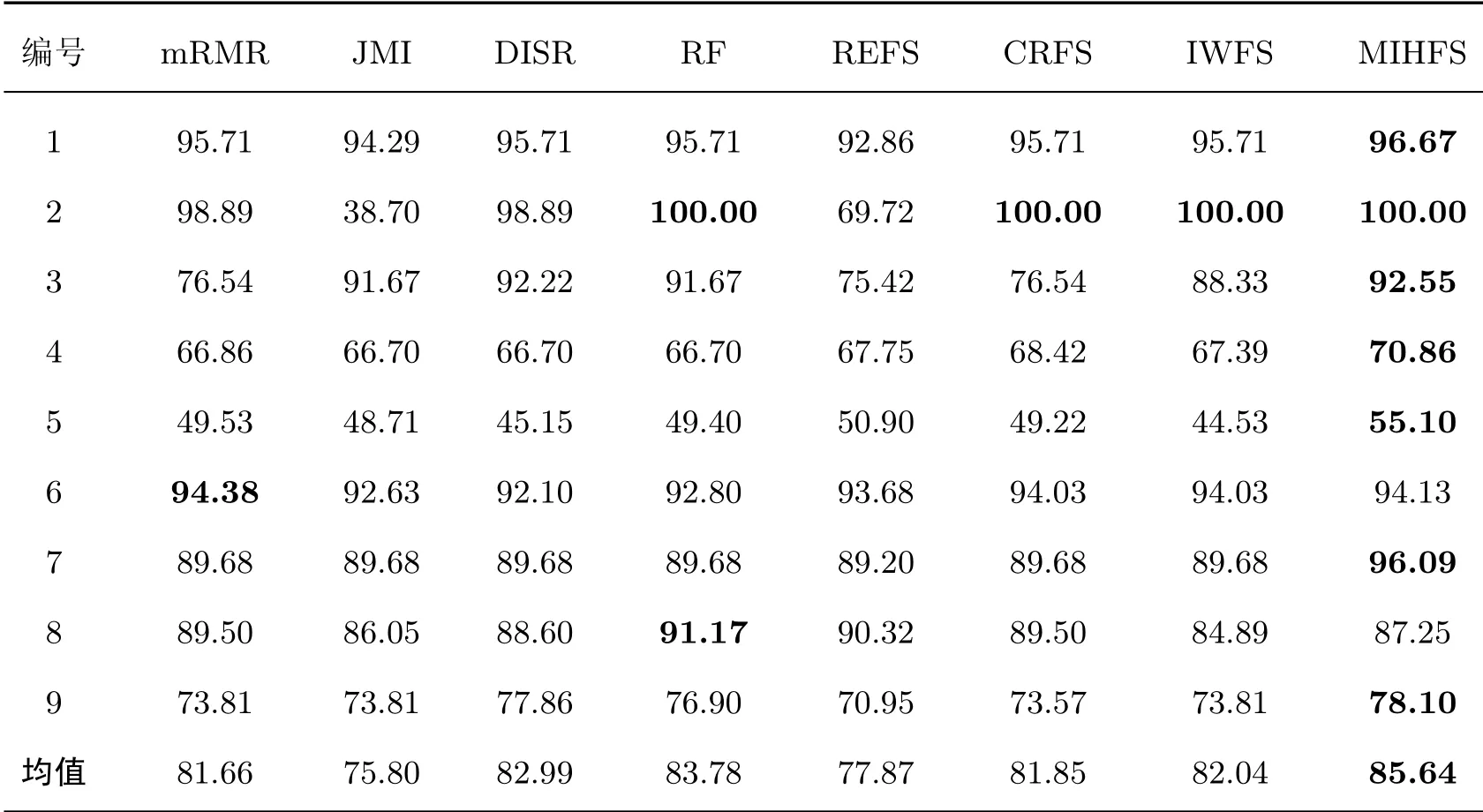
表2 MIHFS算法的分类准确率与其他7种特征选择算法在KNN分类器上的最高分类准确率Table 2 Classif ication accuracy of MIHFS algorithm and the highest classif ication accuracy rate of other seven feature selection algorithms on KNN classif ier %

在特征子集数量方面，特征选择算法应在保持原有信息的情况下保留尽可能少的特征。为了进一步证明本文算法的有效性，通过实验对比了本文算法在不同数据集上所选特征数量以及其他7种特征选择算法在不同数据集上获得KNN最高分类准确率时所选出的特征数量，结果如表3所示。

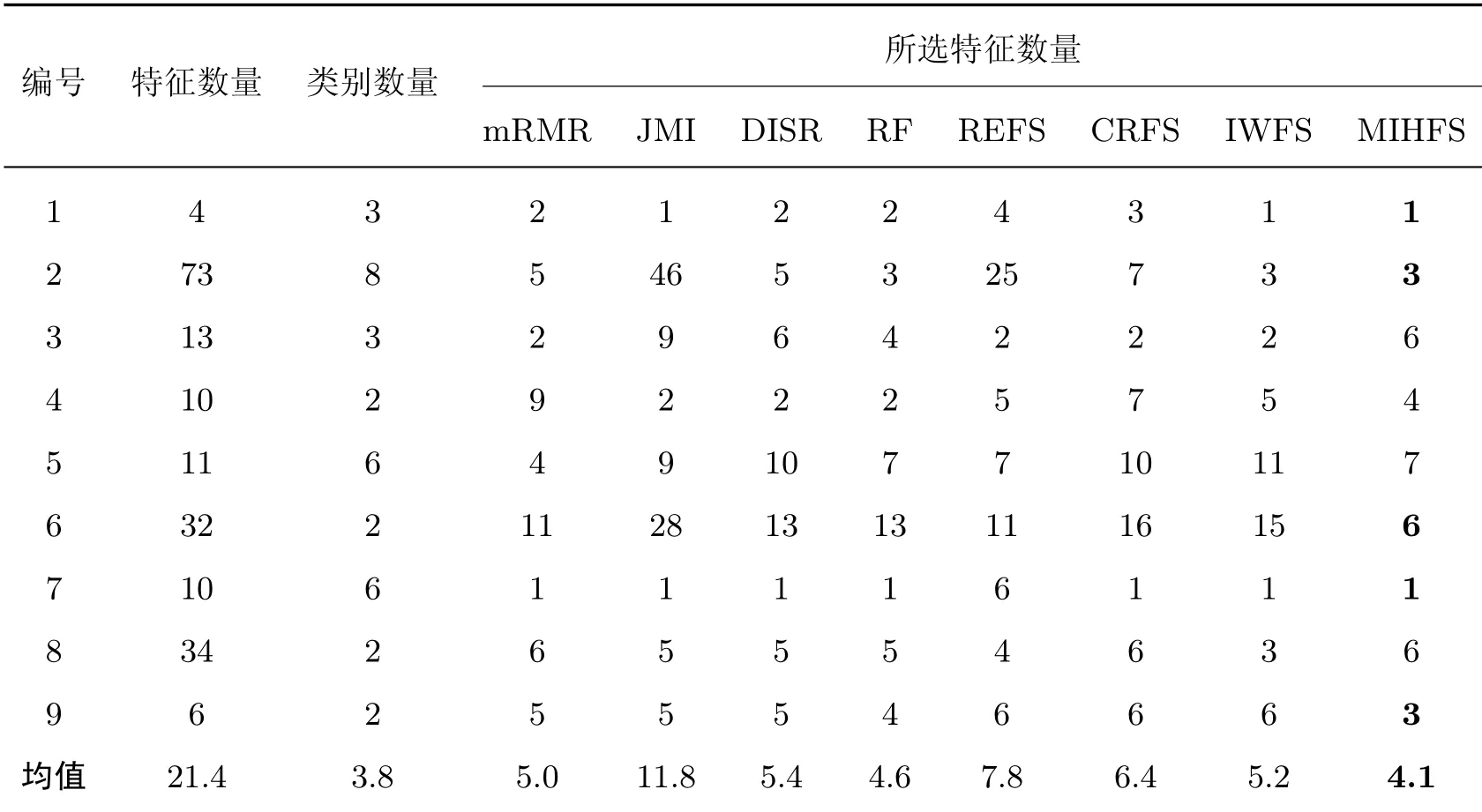
表3 MIHFS算法及其他算法在不同数据集上所选特征的数量Table 3 Number of features selected by MIHFS algorithm and other algorithms in different datasets 个

表3中数据加粗部分表示MIHFS所选特征数量少于其他特征选择算法所选择的特征数量。从表3中可以看出：在保证KNN最高分类准确率的情况下，包括本文算法在内的8种特征选择算法都能有效去除大量候选特征，且本文提出的MIHFS算法在Iris数据集、Cortex_Nuclear数据集、Breast-Cancer-Wisconsin数据集、Glass数据集以及Geological数据集上均保留了最小数量的特征。虽然本文提出的MIHFS算法在其他数据集上并未保留最少数量的特征，但所选特征的平均数量为4.1，小于其他算法的平均数量。因此，MIHFS算法在所选特征数量方面具有明显的优势。

在算法稳定性方面，经10折交叉验证选用Wine数据集评估特征选择算法的稳定性，以推广的Kuncheva指数（Kuncheva index,KI）[25]作为衡量特征选择算法稳定性的度量指标。两个特征子集间的相似性度量为

式中：SA值的范围为[−1,1]，该值越大，说明两个特征子集越相似。当值为1时，两个特征子集完全相同。对所有特征子集的两两相似度平均计算公式为

根据式（16）可以得到各特征选择算法的稳定性值，如表4所示。

从表4中各特征选择算法平均稳定性值的结果来看，MIHFS算法的稳定性最强，其次是RF算法。

表4 特征选择算法的稳定性结果Table 4 Stability results of feature selection algorithms

4 MIHFS算法在油气地质评价中的应用

本文以高邮凹陷永安地区戴一段为实际应用对象，从海拔深度、相对物性、孔隙度、渗透率、隔层厚度和断层泥比率（shale gouge ratio,SGR）六方面对高邮凹陷永安地区戴一段的含油气性进行评价。首先以本文的MIHFS算法筛选出海拔深度、渗透率和断层泥比率3个指标作为最终的评价指标，并用RF算法确定各指标对应的重要性权重为[0.343 9,0.277 8,0.378 4]；然后根据式（13）对原始数据进行归一化处理，处理后的结果如表5所示。

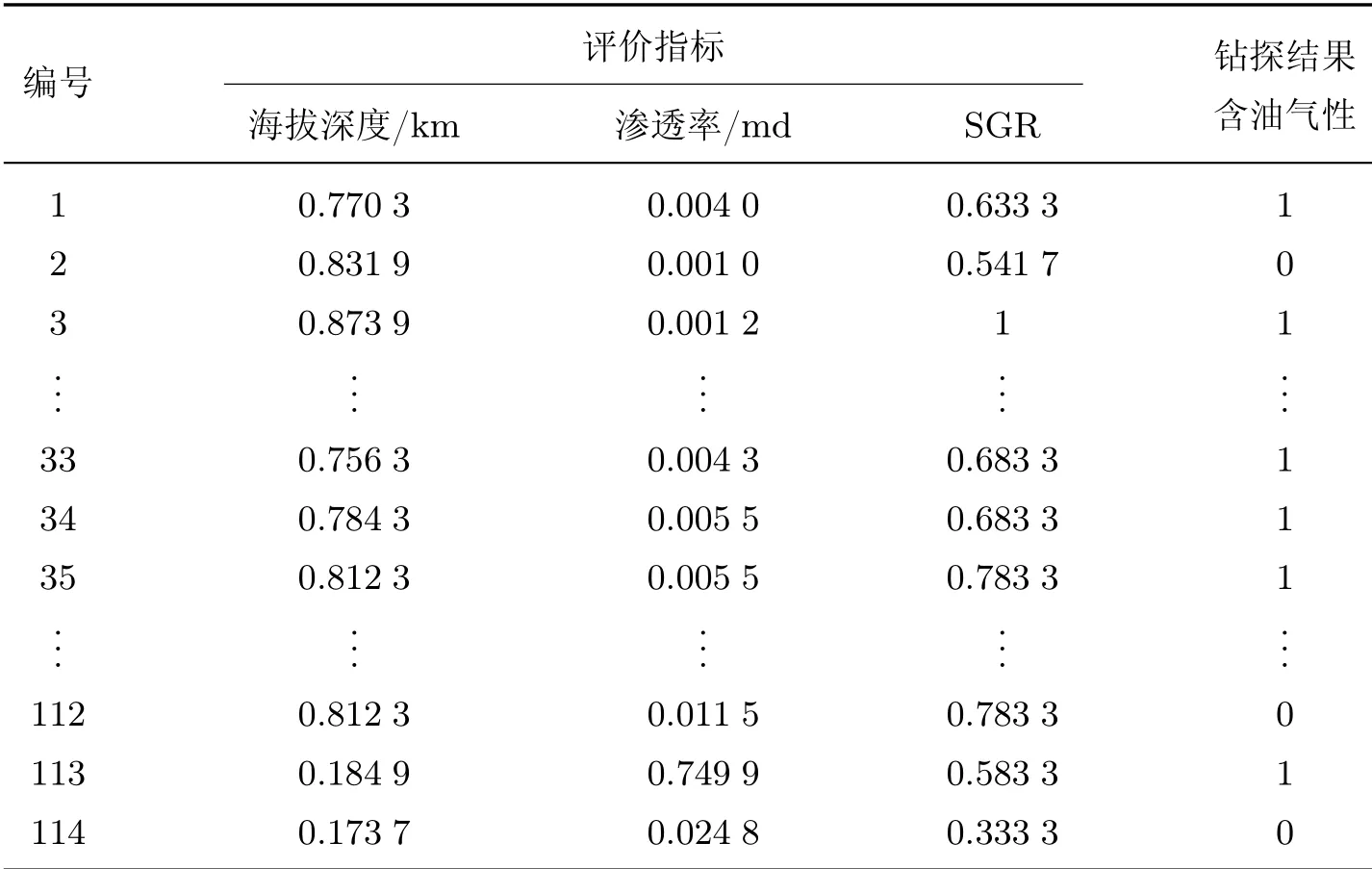
表5 数据归一化处理结果Table 5 Data normalization processing results

灰色关联分析法在信息不完全的情况下具有优势但在整体方法上存在问题，而TOPSIS法不能充分反映每个方案内部因素的变化趋势和理想方案之间的差异，因此本文利用GRATOPSIS法[26]对高邮凹陷永安地区戴一段的含油气性进行评价，得到各样本的综合评价值如表6所示。

表6 评价结果Table 6 Evaluation results

根据综合评价值将样本分为I、II、III、IV共4类：1）综合评价值V≥0.7为I类，评价结果为含油气且概率很高，风险较低，可进行预探井位部署；2）0.5≤V<0.7为II类，评价结果为含油气且概率较高，存在一定的风险，需要进一步确定；3）0.3≤V<0.5为III类，评价结果为不含油气，但存在一定的风险，需要进一步确定；4）V<0.3为IV类，评价结果为不含油气，风险较低。最终结果也如表6所示。

对高邮凹陷永安地区戴一段进行含油气性评价，共评出I类（有利）地区3个，占评价总量的2.63%；II类（较有利）地区51个，占44.74%；III类（较不利）地区53个，占46.49%；IV类（最不利）地区7个，占6.14%。以0.5为分界线判别是否含油气，若综合评价值V≥0.5，说明含油气；反之，则不含油气。在含油气性方面，使用GRA-TOPSIS法对永安地区戴一段的综合评价的评价准确率为80%，具有良好的评价效果。

5 结语

本文在深入研究特征选择算法的基础上对特征相关性、冗余性和交互性进行更准确的刻画，进而提出了一种MIHFS算法，不仅有效去除了冗余特征，而且保留了具有交互作用的特征，且无需事先确定所选特征的数量。从分类准确性、获得最高分类准确率时所选特征的数量和算法稳定性三方面，将本文算法与mRMR等7种特征选择算法在8个公共数据集及地质数据集上进行实验比较。结果表明：本文提出的算法与其他特征选择算法相比具有明显的优势，不仅有效减少了特征数量，而且所选特征具有较好的分类性能。最后将MIHFS算法与GRA-TOPSIS法相结合应用到高邮凹陷永安地区戴一段地质评价中，其评价结果准确率为80%，与实际钻探结果基本吻合，说明该算法具有较好的实际应用价值和前景。