基于三维卷积和CLSTM神经网络的水产养殖溶解氧预测

查玉坤，张其林，赵永标，杭波

湖北文理学院计算机工程学院，湖北襄阳441053

智能水产养殖系统是采用现代信息技术监测水质参数，如溶解氧、水温、p H值、电导率等，有助于实时净化、增加氧气等操作。对于水产品来说，溶解氧支持着生物体的整个新陈代谢过程[1-2]，适宜的溶解氧质量浓度可促进生物生长，缩短育种周期，提高经济效益。溶解氧质量浓度过低则会抑制生物生长，甚至可能导致生物死亡，造成严重的经济损失[3]。

水环境包括水产养殖生物以及各种肉眼无法观察到的微生物。这些微生物与水产养殖生物存在共生关系，其中有些微生物是好氧的，而有些则是厌氧的。水生物在生长过程中必须建立适当的共生关系。在溶解氧变化的动态过程中，各种环境因素之间存在着复杂的相互作用[4]。溶解氧控制方法的实施与这些方法生效之间存在一定的滞后效应，因此在整个养殖周期中必须预测溶解氧的变化趋势，以便尽快实施一定的控制策略来消除这种滞后效应对水产养殖造成的风险。

由于水环境的变化受诸多因素的影响，精确预测较为困难。针对河流、湖泊等不同环境中的水质预测问题，不少学者提出了不同的方法，诸如灰色系统理论[5]、神经网络[6-8]、支持向量机[9-10]、支持向量机与其他方法的融合[11]、自适应神经推理方法[12-13]、小波神经网络[14]等。然而，上述方法存在易陷入局部极小值而导致的结果不准确、模型参数需要优化等问题。文献[15]采用基于聚类的Softplus极限学习机预测水产养殖溶解氧的质量浓度，虽然提高了泛化能力，但预测准确率与BP神经网络相比并没有明显提升。深度学习模型的发展为水产养殖溶解氧的预测提供了有效的解决途径。Ta等[16]提出一种简化的反向理解卷积神经网络（convolutional neural network,CNN）模型，降低了整体计算复杂度，提高了模型的收敛性，但未考虑溶解氧的周期变化规律，于是他们进一步提出了定时衰减矩阵和CNN结合的溶解氧质量浓度预测方法[17]。CNN已广泛应用于解决各种问题[18-20]，如科学论文分类[21]、心电图检测[22]。CNN直接输入原始数据，通过卷积、池化等一系列操作提取特征，在提高抽象层次的过程中实现内容的精确识别。同时溶解氧预测也是一个时间序列问题，在水中质量浓度的变化趋势与水温、电导率、pH值等影响因子的变化趋势有着复杂的非线性关系[4]。例如：p H值越小，水的酸性越强，极性越大，而O2是非极性分子，溶解度会随pH值的下降而略有下降。针对上述特点，本文提出一种基于三维CNN和卷积长短期记忆（convolutional long short-term memory,CLSTM）神经网络模型来预测循环水产养殖溶解氧，利用CLSTM神经网络模型提取时间维度的特征，捕获长期依赖性，更灵敏更精准地预测目的数据在时间维度的变化规律。

1 基于三维卷积和CLSTM神经网络的溶解氧预测模型

本文提出的模型结构如图1所示。首先将电导率、水温、溶氧、pH值所组成的原始向量乘以它的转置得到一个4×4的单通道矩阵，再将前后10个时间点的数据组成一个三维矩阵，用4个1×2×2（深度、长度、宽度）的过滤器对输入矩阵进行三维卷积操作，通过4个过滤器的卷积得到4个10×3×3三维矩阵，从而得到第1个卷积层（Conv3D_1）。第1卷积层的深度也称为通道，等于过滤器的数目。在第1个卷积层的基础上，用相同大小的过滤器得到第2个卷积层（Conv3D_2），即4个10×2×2的矩阵。然后，将两次卷积后的结果送入卷积长短期记忆层进一步提取时间维度上的特征。最后，经拉伸过程将多维矩阵变换成一个向量后送入全连接层处理。

图1 基于三维CNN和CLSTM的神经网络模型Figure 1 Neural network model based on 3D CNN and CLSTM

1.1 输入向量的自乘

CNN最重要的特征是以高维矩阵作为输入，在卷积过程中利用共享权值和共享偏差获取特征。假定C表示电导率、T表示水温、D表示溶氧的质量浓度、H表示pH值。为了得到各参数之间的不确定关系，同时符合CNN的输入特性，将这4个参数组成一个输入向量乘以它的转置，得到一个4行4列的对称矩阵，表达任意两个参数的所有组合。在时间维度上取样，形成三维矩阵作为输入向量。设Z=(C,T,D,H)T，则

1.2 反向理解两个连续卷积的细化提取过程

在CNN中，图像从最底层的点开始逐层识别直至更高内容层上的点。在此过程中，通过卷积运算和池化层简化特征提取，提高抽象层次，实现更准确的判断。同一层次的卷积用不同的方法识别图像不同部分在同一层次的表示。每一个局部接受域描述了图像的一个潜在特征，前一层的卷积引导后一层的卷积，从而提升抽象层次。由于溶解氧质量浓度的变化是一个连续的动态过程，且与温度、p H、电导率等水质参数之间存在复杂的相互作用，很难用精确的数学模型来描述。揭示这种关系的过程是一个细化的过程，即抽象的逆向过程。向量自乘矩阵是各种因素之间的组合关系，而反向理解CNN中的第1个卷积是对4个因素的第1个潜在关系的细化，第2个卷积是对第1个卷积的进一步处理。这两个关系的细化过程可以确定输入参数之间的潜在影响关系。除此之外，这4个参数被细化为4×4=16个参数，表示参数之间的潜在关系。输入矩阵的两个连续卷积过程如图2所示。

图2 两个连续卷积过程Figure 2 Two continuous convolution processes

输入向量通过自乘得到输入矩阵，按参数名称在水平坐标和垂直坐标上进行标记，例如输入向量Z12为

第1次卷积采用4个过滤器，且卷积过滤器大小为1×2×2。第1个“1”表示深度，即每次三维卷积操作处理的二维矩阵数目，因此第1个卷积层有1×2×2×4+4=20个参数；最后一个“4”表示每一层的共享偏差(BL1,BL2,BL3,BL4)。第1次卷积运算公式如下：

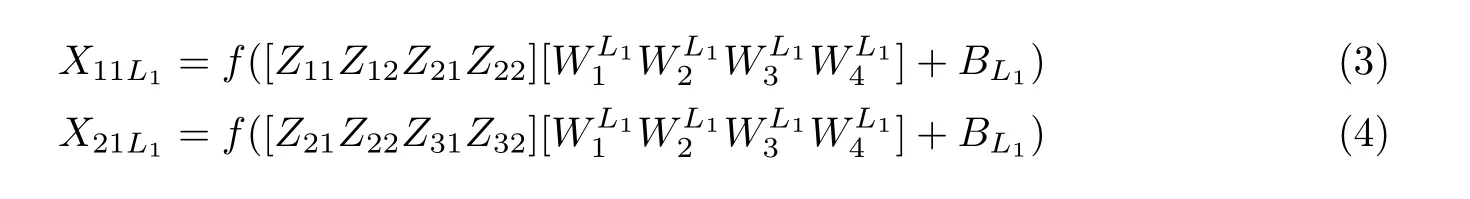
式中：f为修正线性单元（rectif ied linear unit,ReLU）的非线性变换函数，表示为f(x)=max(x,0)；Xxyz为卷积结果，x和y为层中的位置标识符，z为通道深度（层）；为共享权值，取值范围为(0,1)，其中Li为输出矩阵通道深度，则每个大小为2×2的过滤器对于输入层都有2×2=4个共享权值；BLi表示范围为(0,1)的共享偏差。

第2次卷积与第1次卷积相似，也采用4个过滤器。输入为第1次卷积层，共有2×2×4×4+4=68个参数。第2次卷积运算公式为

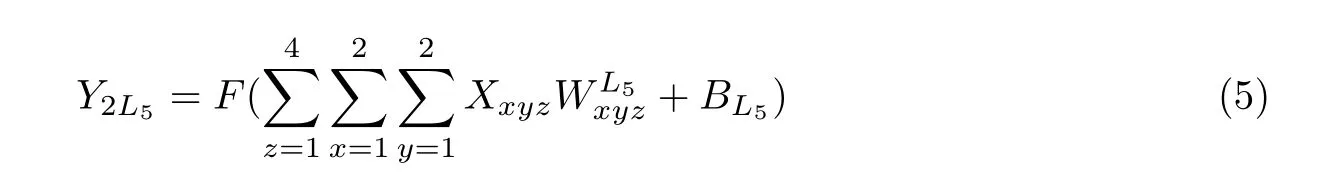
然后将两次卷积后的160(10×2×2×4)个元素送入卷积长短期记忆层进一步处理。

1.3 删除池化层

从1.1节和1.2节的讨论可以看出，反向理解CNN的所有操作是为了确定输入参数之间的潜在关系，而不是抽象特征。在原始CNN中，卷积层之后的池化层用作提取特征和简化计算，以进一步提高抽象层次，其本质特征是先简化计算后提取特征。这一作用与本文提出的细化参数之间的关系并不一致，因此本文模型在传统CNN模型的基础上删除池化层，既可以满足初始设想参数的细化要求，又可以降低整个模型的计算复杂性，使CNN更加实用。

1.4 CLSTM模型

Hochreiter和Schmidhuber于1997年提出长短期记忆（long short-term memory,LSTM）网络模型，有效地解决了循环神经网络（recurrent neural network,RNN）的梯度消失问题。LSTM的遗忘机制也与人类记忆的特点有许多相似之处[23]。后来出现了诸多改进的LSTM[24-25]，比较著名的是由Cho等[26]提出的门控循环单元（gated recurrent unit,GRU），它将忘记门和输入门合成了一个单一的更新门，还混合了细胞状态和隐藏状态，因此最终的模型比标准的LSTM模型更简单。考虑到LSTM在时序数据处理中的优势，将LSTM与卷积操作相结合，能更加有效地提取图像或者二维矩阵的特征，如文献[27]提出了CLSTM模型，不仅可以像LSTM一样建立时序关系，而且可以像CNN一样刻画局部空间特征，在获取时空关系上比LSTM更好。

循环养殖系统中溶解氧的预测就是一个时空序列问题，从前面的讨论中可知输入数据经过两次三维卷积得到10×2×2×4的多维矩阵。其中：“10”表示时间维度，每10个时间点的数据作为单次数据输入模型；“2”表示矩阵的长和宽；“4”表示深度，即通道数目。多维矩阵在CLSTM模型中的处理过程如图3所示。

图3 多维矩阵在CLSTM模型中的处理过程Figure 3 Process of multidimensional matrices in a CLSTM model

LSTM网络由input gate,forget gate,cell,output gate,hidden共5个模块组成，通常用全连接作为不同状态之间的转换，而CLSTM用卷积作为不同状态之间的转换。CLSTM cell的内部结构如图4所示。

图4 CLSTM cell的内部结构Figure 4 Internal structure of CLSTM cell

CLSTM的工作原理可以表示如下：

式中：it、ft、Ct、Ot、Ht对应input gate、forget gate、cell、output gate、hidden共5个模块；“°”表示矩阵对应元素相乘，又称为Hadamard乘积；“*”表示卷积，σ和tanh为激活函数；Wxi、Wxf、Wxc、Wxo分别为Xt的权重矩阵；Whi、Whf、Whc、Who分别为Ht−1的权重矩阵；Wci、Wcf、Wco分别为Ct的权重矩阵；b为共享偏差；t表示时间序列上不同的时间点。

输入数据经过两次卷积得到通道数目（深度）为4的10×2×2的矩阵。如图3所示，将其按第1维度（时间维度）展开后作为X输入至CLSTM层，得到2×2×4的矩阵，然后将矩阵中16个元素拉伸为向量送入全连接层。

2 实验及结果

2.1 数据来源

实验数据来源于湖北省襄阳市某家特种水产养殖有限公司。在养殖池安装在线监测系统，获取温度和溶解氧数据，离线测量pH值和电导率，由此得到水环境的变化原始数据。训练样本数据有2 500例，测试样本数据有500例。训练集的原始数据如图5所示。

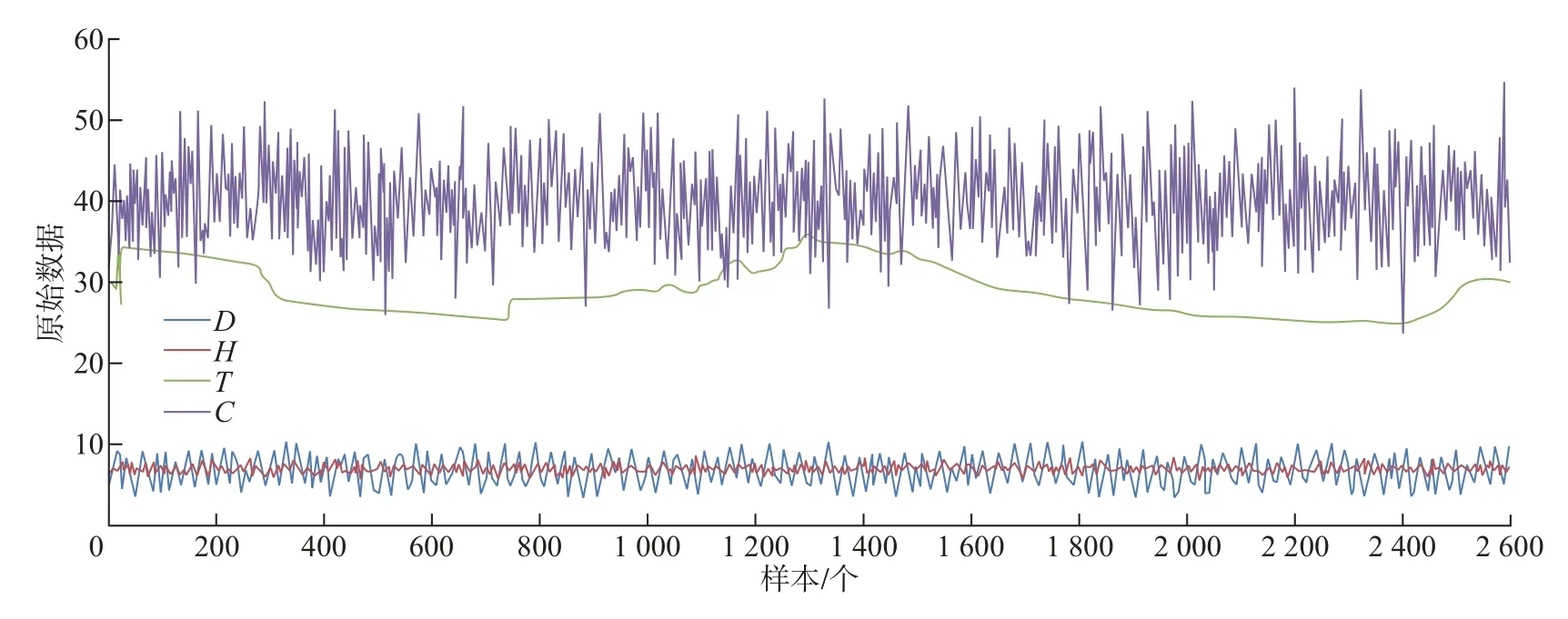
图5 训练集原始数据Figure 5 Raw data in training set

2.2 实验设计

为了验证本文方法的有效性，将本文方法与BP神经网络、Conv3D、Conv2D进行对比实验。实验中使用相同的初始数据，采用相同的训练和优化方法。简化后的BP神经网络框架采用32×16×8的结构，输入参数为(C,T,D,H)T，如图6所示。

图6 BP神经网络模型结构Figure 6 Structure of BP neural network model

模型代码在谷歌的Tensorf low2.0框架中编写，采用Numpy和Pandas库实现矩阵操作和格式转换。实验的硬件环境如下：CPU为Intel core i7-9800X，GPU为NVIDIAGTX 1060，内存为16GB DDR4 2666Hz。在模型的卷积部分，卷积模式为padding=“valid”(edge nonzero f ill)，f ilter参数为1×2×2×4，step stride为1，并以“ReLU”非线性变换函数作为激活函数。在CLSTM部分，使用padding=“same”的卷积模式，kernel size为2，也将“ReLU”非线性变换函数用作激活函数。具体流程如图7所示。

图7 模型代码实现流程Figure 7 Implementation process of model code

在全连接层的BP神经网络中，以均方误差（mean square error,MSE）计算mini_batch为5的误差，MSE计算公式为

式中：Dt为预测值，D为真值。采用L2正则化对模型优化，其计算公式为

式中：Wi表示全连接层的第i个权值(i=1,2,3)。根据MSE可知最终损失函数为

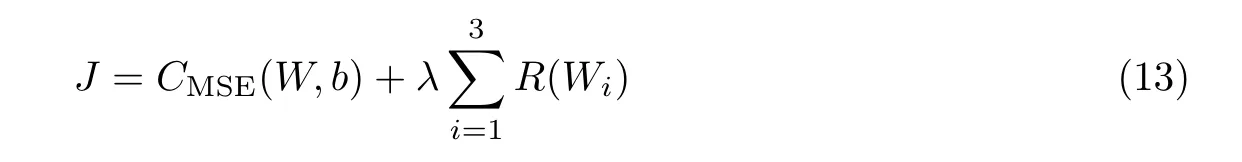
式中：b为模型的总体偏差。正则化部分为损失函数的惩罚项，控制系数为λ，根据经验取值为0.01。

将实验数据进行归一化处理，设定200个训练周期，学习率η=0.001，采用Adam优化器，获取mini_batch数据的J值，并以该值执行反向梯度更新。全连接层的更新公式为

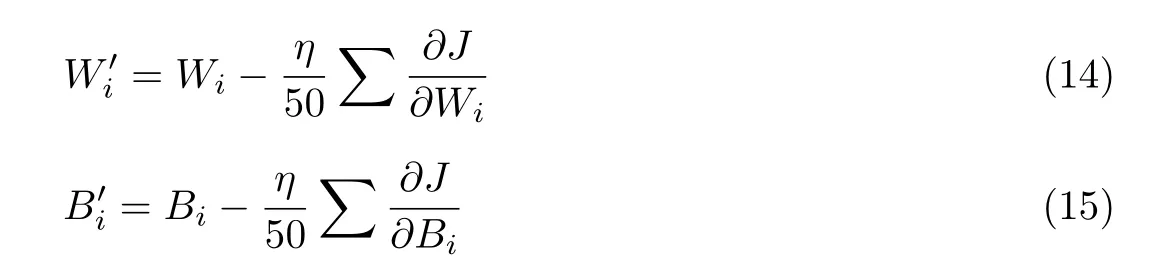
2.3 实验结果

2.3.1 收敛性分析

为了从不同的角度比较不同的方法，将2 500例实验数据进行200次迭代训练。由于后面150个周期的MSE值太小，只绘制了前50周期。分别用不同颜色实线表示不同模型的动态训练过程，如图8所示。其中：横坐标为训练步数，纵坐标为MSE值。

图8 4种模型训练过程Figure 8 Training processes of four models

由图8可知4种方法在训练过程中虽然变化趋势相似，但差异比较明显。在传统BP算法和Conv2D模型的早期波动中，收敛速度相对较慢。因此，在数据量相同的情况下，传统BP算法和Conv2D需要训练更多的步数才能达到精度要求。对于常规的模型更新，需要在尽可能短的时间内训练模型，尽量降低对水质的影响程度。Conv3D+CLSTM模型和Conv3D模型可以在较短的时间内达到一定的的精度值，但Conv3D+CLSTM模型收敛更快。按图8中显示的曲线数据进行计算，得到4种方法的平均MSE如表1所示。

表1 平均MSETable 1 Average MSE

由表1可以看出，Conv3D+CLSTM模型在早期收敛性和稳定性方面具有更好的性能。

2.3.2 预测结果分析

Conv3D+CLSTM模型和另外3种模型训练完成后，得到500个测试样本的预测结果如图9所示。

图9 预测结果比较Figure 9 Comparison of prediction results

由图9可知4个模型均可以捕捉到真实溶解氧数据的变化趋势。传统的BP算法会产生较大的波动，降低预测精度。这些波动通常伴随着参数的突然变化而发生，选取图9中预测误差较大的样本点，如表2所示。可见BP模型在预测过程中的灵敏度不够，Conv3D和Conv2D在预测精度上优于BP模型，但逊于Conv3D+CLSTM模型。主要原因是融入CLSTM后，Conv3D+CLSTM模型对各个参数因子的变化更加敏感，所以能捕捉到这些数据波动的细微变化，保持较高的预测精度。

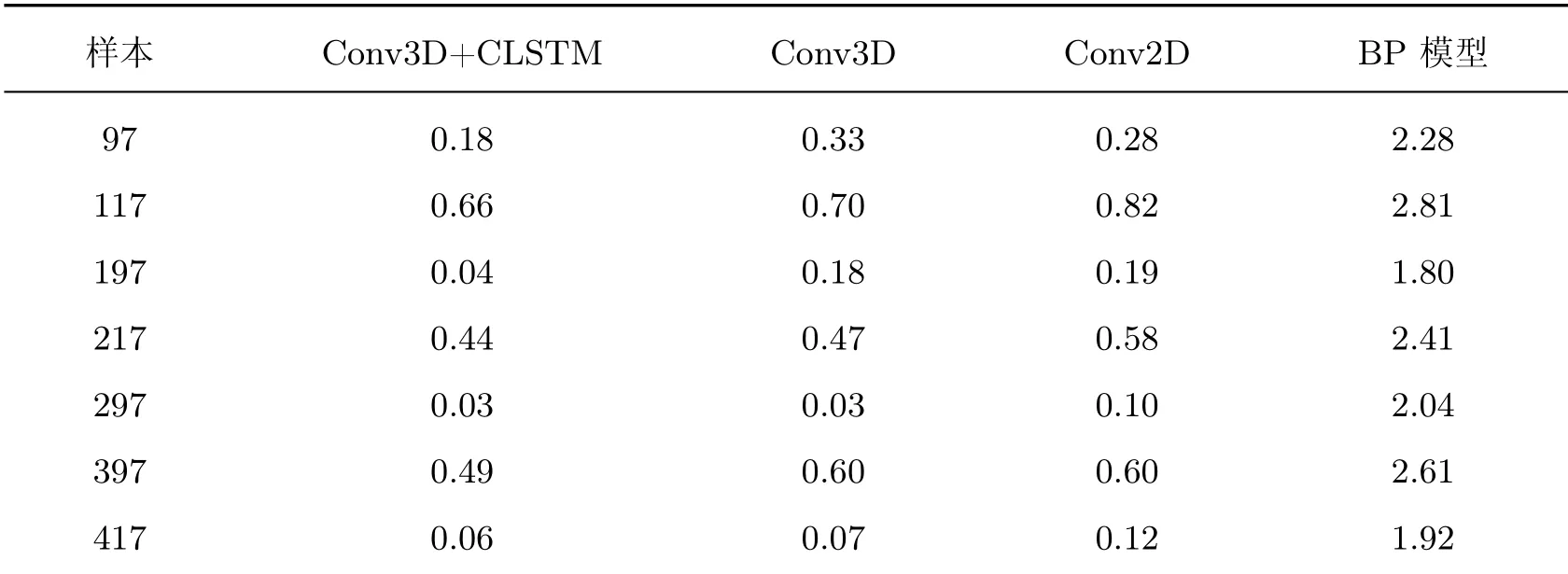
表2 部分样本溶氧预测误差Table 2 Dissolved oxygen prediction error of some samples mg/L

3 结论

本文提出一种基于三维卷积和CLSTM神经网络模型的水产养殖溶解氧预测模型，将输入数据连续进行两次三维卷积运算来细化溶解氧相关因素的特征；然后利用CLSTM神经网络模型提取时间维度特征。将本文模型与BP神经网络模型、Conv3D、Conv2D进行实验比较，可以得出以下结论：

1）总体而言，Conv3D+CLSTM模型收敛速度快，偏差也较小，优于其他3种模型。这种快速的收敛对工业应用尤其重要。

2）在拟合和预测稳定性方面，Conv3D+CLSTM也同样出色。由图8可知，损失值在整个训练过程中持续下降，可见本文模型有着比另外3种模型更快的收敛速度。由图9中可知，Conv3D+CLSTM模型的预测值始终保持稳定，可以捕捉到数据的波动情况，与真实值有良好的拟合关系。

3）影响溶解氧值的各种因素之间存在复杂的非线性关系。在全连接部分，输入是参数之间关系的细化值，而不是具体的参数。将连续卷积求出的潜在特征值提供给模型，可以得到更快的训练收敛速度以及更高的预测精度和预测稳定性。因此，将更多维度的特征细化能够获得更加准确的结果。然而，这些更精确的结果需要更多的计算量，从而增加了计算成本。如何权衡精度与成本，将是今后的研究方向。