双臂护理机器人抱举重心稳定性研究
2022-01-19夏建强苗新刚许会超
夏建强 苗新刚,2 许会超
(1安徽恒利增材制造科技有限公司,安徽芜湖,241200; 2北京建筑大学,北京市建筑安全监测工程技术研究中心, 北京,100044; 3 北京电子工程总体研究所,北京,100854)
0 引言
护理机器人辅助医护人员对病人进行康复护理,将医护人员从繁重的体力劳动中解放出来,己经成为康复护理领域研究的热点问题[1]。护理机器人在进行护理任务、辅助医护人员对病人进行康复护理、完成对病人的平稳转移时,整个运动过程中的运动稳定性是最令人关心的问题,直接关系到护理任务的成败[2-3]。
对于护理机器人来说,其倾翻的危害远比侧滑严重,在抱起病人过程中如果发生倾翻,那么对病人二次伤害的后果是无法想象的[4]。
仿人机器人与传统的轮式机器人相比,其稳定性更值得研究,仿人机器人稳定性的判断依据有很多种类型,其中最主要的是 ZMP、FRI、COP等[5]。这几种判断依据都有一定的使用限制范围,迄今为止,还没有一种判断依据可以完全取代其他类型[6]。
稳定的支撑是获得理想运动的重要条件,稳定区域即机器人各轮与地面的接触点构成的凸多边形在水平方向上的投影,当仿人护理机器人的双臂、腰部、躯干及头部在一定的位姿状态下,其整体重心、在水平方向的投影位于稳定区域内时,机器人即处于稳定状态。
采用零力矩点ZMP动态稳定判据,是本文解决重心稳定性的重要理论依据,本文以此为基础对机器人运动进行分析。
1 护理机器人结构
本文设计的护理机器人由底盘框架、腰部、躯干、双臂和简单手掌部分组成,其结合了轮式机器人和人形机器人的各自优势特点,灵活便于控制,稳定性良好,既増加护理机器人的灵活使用性,又拓展了其工作范围。护理机器人机械结构如图1所示。

图1 护理机器人结构
护理机器人涵盖了智能轮椅和护理床的优点,既能辅助医护人员转移病人,又能满足家庭和医院日常护理中的多样化需求,其双臂与移动基座的配合,极大地拓展了护理机器人的操作范围。
2 重心稳定性分析
护理机器人按照己规划好的轨迹路径抱举病人时,通过各关节协调配合来保证底盘、躯干和双臂运动过程中整个系统的ZMP点,位于轮子与地面接触点形成的支撑多边形(稳定区域)内,护理机器人处于动态稳定。
护理机器人的4个全向轮与地面的接触点围成一个矩形,以边平行于Z轴和Y轴的矩形中心为原点,原点到矩形轮廓边界的最小距离r0为半径的圆,此区域本文定义为有效稳定安全区域,如图2所示。
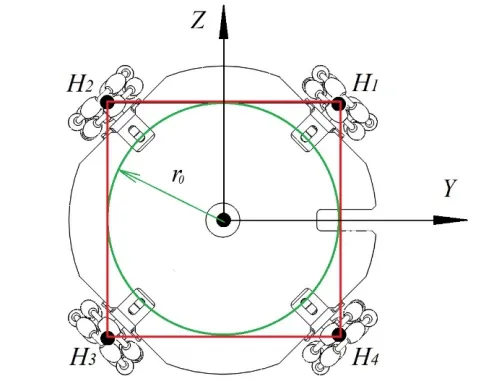
图2 机器人的有效稳定安全区域
若 上述ZMP点处于有效稳定安全区域外,则无法保证护理机器人是否处于稳定状态,此时需要调整各构件的运动参数,使系统的ZMP点调整到稳定有效区域内,具体判定公式为:
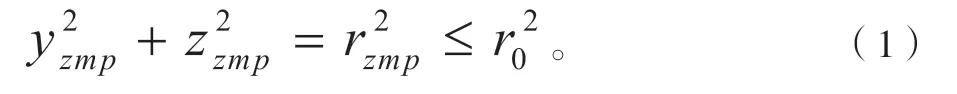
在SolidWorks中,设置模型的真实材料和质量,可以从系统中测量出护理机器人各个部位的重心参数,如表1所示。

表1 护理机器人重心参数表
根据机器人各部分的质心位置和质量参数,可以计算护理机器人在抱取病人时的不稳定边界的位置(等效质心位置),见式(2):

在式(2)中,mc为负荷质量。当mc为40kg时,Dmax=330mm。mc取不同值时,倾倒边界位置Dmax的变化如图3所示。

图3 倾倒边界随负荷质量变化曲线
从图3可以看出,当护理机器人无抱取任务时,倾倒边界距离稳定区域最远,发生倾倒的可能性最小;随着抱取负荷质量的增加,倾倒边界距离稳定区域越来越近,稳定区域越来越小,此时越容易发生倾倒。
由ZMP得到关于YOZ平面上任一点Pzmp的力矩平衡式见公式(3)。
以稳定区域中心建立坐标系,ZMP点Pzmp为(yzmp,zzmp),式(3)中ri为质心位置矢量,ΣT为受到合外力矩,g为重力加速度。
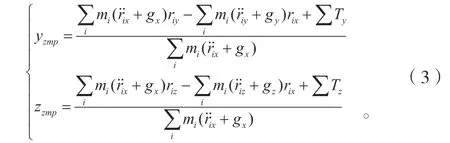
由于护理机器人躯干在整个护理过程中运动缓慢,考虑忽略其惯性力/力矩,由此可得到护理机器人ZMP点简化计算公式(4):

式(4)中,fx1为部件作用在底盘上沿x轴方向的合外力(包含惯性力),nz1为部件作用在底盘上绕z轴的合外力矩(包含惯性力矩),ny1为部件作用在底盘上绕y轴的合外力矩(包含惯性力矩)。
当机器人抱取位置为最远距离,且双臂一致前伸时,由此可以得到机器人ZMP点为最不稳定的点,计算得到rzmp(rmax)的值为357mm。
当rzmp≤r0=272mm时,点Pzmp在主稳定区域,为了定量分析不同区域稳定性程度的大小,设定在主稳定区域的点的稳定度都为1,次稳定区域的点的稳定度根据rzmp的r0的差值乘以一定的系数得到。
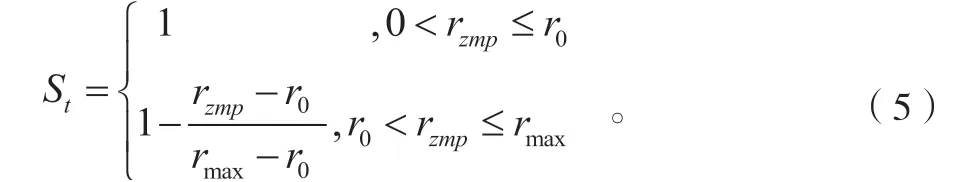
总之,ZMP点越接近主稳定区域,则护理机器人的稳定系数越高。通过以上分析,笔者把重心稳定性判定的理论应用于优化轨迹规划,并作为运动规划的参考标准。
3 安全路径的运动控制分析
由于护理机器人在运动过程中,护理对象的重心基本在其小臂的中间位置,所以其双臂的轨迹规划问题就转换为中间点的轨迹规划。
本文研究的目的就是要提高机器人运动过程中的安全性,安全性是由系统重心稳定度决定的,由机器人的动力学方程可知,系统的稳定度是机器人关节运动的函数,通过逆解算法可以规划机器人关节运动,提高机器人运动的安全性。
轨迹规划是从当前位置到目标位置的路径形状,在预定任务进行之前,需设定机器人的当前位姿,因为规划的是双臂末端的中间点,所以需要从护理机器人双臂位姿确定当前位姿和目标位姿。
该中间点的当前位姿为:

式(6)的矩阵作为路径规划的起始位置,由护理机器人左臂和右臂的末端位姿矩阵得到。
正向抱取运动是护理机器人最简单的运动形式,主要是向前伸出双臂来接近平躺的护理对象。因为规划的是双臂末端的中间点,所以需要从双臂位姿确定当前位姿和目标位姿。
该中间点的目标位姿为:

最优稳定性轨迹规划的规划目标是平均稳定度St,所以以St为目标优化函数,利用基本遗传算法求得路径点。
设n=20,t=20s,由MATLAB仿真中的二阶抛物线函数拟合,路径点的拟合曲线如图4所示。

图4 最优稳定性路径点轨迹图
从图4中可以看出,最优路径基本趋于一条直线,而且在Z轴的偏差很小,此路径形状可以作为理论最优规划路径。
根据护理机器人始末位置的位姿,可以选择常用的两种路径形状规划,即分别用直线和圆弧去规划中间点的当前位置到目标位置的运动,如图5所示。

图5 护理机器人抱举路径形状图
笔者根据结构参数、逆运动学解、路径形状以及平均稳定度的数学模型公式,求得:
圆弧轨迹的平均稳定度Stc=0.021 ;
直线轨迹Stl=0.047。
可以看出,直线路径形状的平均稳定度大于圆弧路径形状的平均稳定度,也就是说,直线轨迹的安全性优于圆弧的安全性。
至此,直线路径形状跟最优规划路径基本一致。
4 实验
本文采用轮辐式压力称重传感器用于测量4个全向轮与地面的压力,从而间接测量稳定程度。系统通过一定的频率采集数据,并且把数据以Excel格式存入计算机,分析数据时可以直接从计算机中导出。
为了证明本设计的护理机器人的重心稳定性,笔者在护理机器人双臂各负重20kg的砝码,即总负重为40kg进行测试。
MATLAB的优化结果和ZMP的计算结果证明:所规划的运动能够实现仿人机器人的重心最优稳定性。
根据COP的定义,笔者在护理机器人的脚底安装4个压力传感器。利用物理样机,在护理机器人的实验平台上进行抱取动作的实验,并利用重力测试传感系统采集运动过程中4个全向轮对地面的压力变化。
4个压力传感器上表面与全向轮接触,下表面直接和地面接触,所测量的压力值也就是轮子对地面的压力。采集的数据导出后,然后等间距取出10个数据点,通过COP计算公式得到稳定性判定的数值,然后再利用MATLAB拟合出变化曲线。

在式(8)中,FR1,FR2,FR3和FR4为压力传感器测得的压力值,l1,l2,l3和l4为压力传感器与平台中心位置的距离。
针对前面提到的两种运动任务,本文采取正向抱取和侧向抱取,并通过物理样机进行验证。
重力测量系统的数据采集频率是1Hz,实验的时间为20s,从系统软件里导出数据格式为Excel数据,分别等间隔抽取4个传感器采集的10个数据,列表如表2所示。
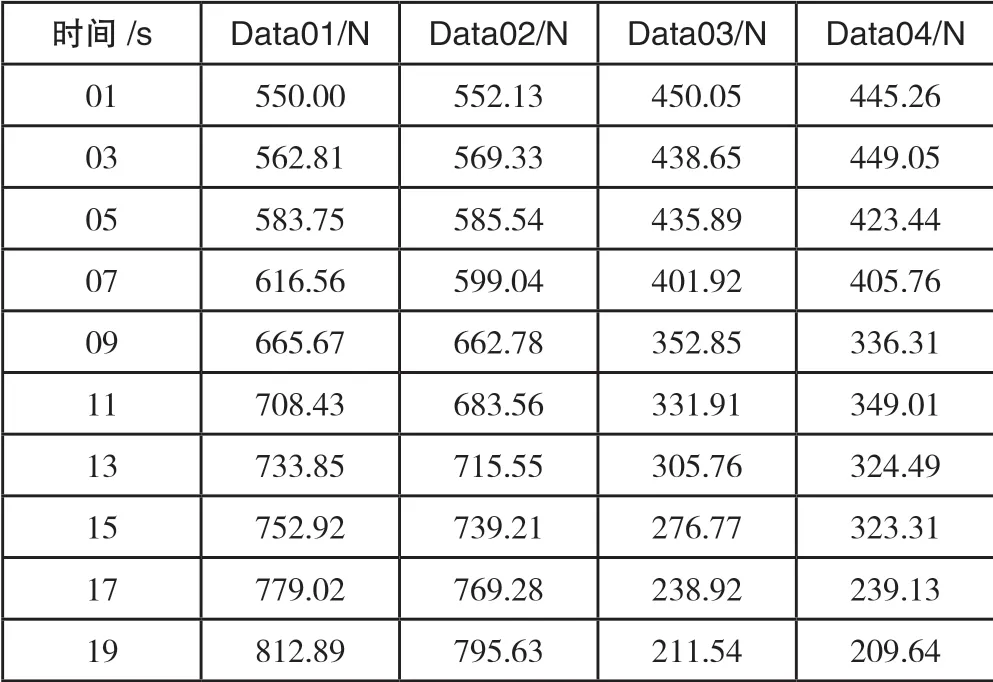
表2 正向运动传感器压力值数据采集表
根据表2中数据,通过COP计算公式得到稳定性判定的数值与中间点Y轴位置坐标的变化数据,然后用MATLAB中的二阶抛物线函数拟合,曲线如图6所示。

图6 COP参数值与中间点Y轴位置的变化
5 结论
本文对护理机器人在执行“抱起病人”这一典型护理任务过程中的稳定性做了深入研究,分析了重心对护理机器人的运动稳定性的影响;主要考虑护理机器人运动过程中重力对稳定性的影响,采用零力矩点ZMP动态稳定判据,从而尽可能地得到符合实际情况的结果;在满足ZMP约束的情况下进行机器人轨迹规划,使护理机器人在两工作点之间或沿规定轨迹运动的安全最优。分析结果表明,该规划算法能够显著提高护理机器人的工作安全性,对实际护理机器人的轨迹规划具有一定的理论指导意义。
实验通过位置控制驱动护理机器人按照最优轨迹规划的路径进行运动,同时应用重力测试系统采集数据,最后根据采集的数据对实验结果进行分析,验证了本规划的合理性。
