旱涝不稳定度的定量化研究及应用

邵 进，李 毅，宋松柏

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

干旱是层次最多、了解最少、破坏性最强的自然灾害之一[1-2]，由于缺乏充分描述干旱现象的定义，一直困扰着干旱的监测与分析[3]。标准化降水指数(SPI)模型是在时空上计算干旱影响及其强度的一个有效工具, 它所反映出的干旱信息与实际观测结果基本一致[4-7]。Caccamo等[8]指出，结合遥感技术应用NDVI进行干旱监测效果较好，Shahabfar等[9]研究了干旱垂直指数在伊朗干旱监测中的适用性，司昌亮等[10]研究了星星哨灌区1954-2009年各干旱等级的变化情况及发展趋势。

关中地区又称关中平原或关中盆地，指陕西秦岭北麓的渭河下游冲积平原，平均海拔约500 m，其北部为陕北黄土高原，南部则是陕南山地、秦巴山脉， 总面积约5.55万km2。除凤县、太白县基本属于长江流域以外，其余均属黄河流域。关中地区为全国16个重点建设地区之一，但它深处内陆，水资源贫乏，生态环境脆弱，因此研究关中地区不同时期旱涝变化的时空分布及其变化规律，对指导该地区工农业经济发展具有一定的价值和意义。关中地区42个气象站点的空间分布如图1所示。

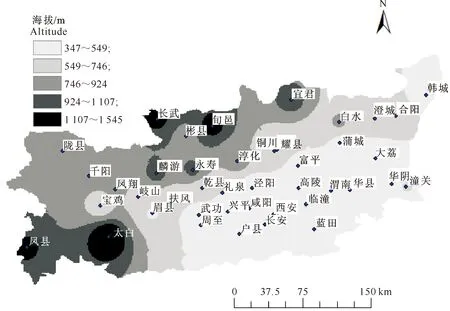
图 1 陕西关中地区的气象站点分布

目前，对干旱监测与评估的研究较多，但缺乏对不同时期旱涝变化剧烈程度的量化研究成果。本研究定量分析了关中地区旱涝变化剧烈程度的时空分布及其变化规律，拟提炼出一个既能较好地反映旱涝变化剧烈程度又比较简单实用的评价指标，进而为旱涝的预测、防灾减灾以及水资源的合理规划与利用提供支持。

1 原理与方法

1.1 旱涝不稳定度的计算

在人们的普遍认识中，某种事物从一种状态变化为另一种状态的幅度越大，这个变化过程就越剧烈，就认为该事物越不稳定。了解事物变化剧烈程度的特征，有助于对事物未来所处状态的预报。

参照《气象干旱等级》(GB/T20481-2006)和《中华人民共和国国家标准农业干旱预警等级》(GB-4(2))将旱涝的程度划分为9个等级，每个等级的状态值为am(m=1，2，…，9)，且am的取值为整数。令特旱取a1=-4，重旱取a2=-3，中旱取a3=-2，轻旱取a4=-1，正常取a5=0，轻涝取a6=1，中涝取a7=2，重涝取a8=3，特涝取a9=4。由于SPI用于旱涝的监测和评估效果较好，因此本研究应用SPI进行旱涝等级的评价，具体的计算和分级见文献[11-14]。

假设相邻2个时段旱涝的状态值分别取前期为a1i和后期为a2j(下标1，2分别表示前期与后期；i，j=1，2，…，9，均分别表示9种不同的状态)，则前期状态到后期状态的变化幅度为|a2j-a1i|，而前期状态到后期状态可以变化的幅度应该为|am-a1i|共9个值，现定义以下几个概念：

不稳定度指前期状态到后期状态的变化幅度与前期状态到后期状态可以变化幅度最大值的比值，即为该时段内旱涝的不稳定度，简称不稳定度。其计算公式如下：

(1)

式中：η为不稳定度，0≤η≤1；|am-a1i|max为旱涝状态值变化幅度的最大值。

平均不稳定度指系列不稳定度的平均值，计算公式为：

(2)

式中：n为序列的长度，t为序列的次序号，ηt为序列中第t个不稳定度。

1.2 旱涝不稳定度分析变量的计算

将趋势线斜率k、均方差σ和变差系数Cv作为3个分析变量，分别用于研究不稳定度沿时序的总体变化趋势、离散程度以及相对离散程度。假设不稳定度的时间序列为η1，η2，…，ηn，而x1和x2是其时序分布趋势线上的任意两点，t1、t2是对应的年份，则3个变量的计算公式为：

(3)

(4)

(5)

2 关中地区旱涝不稳定度实例分析

本研究首先应用SPI指标评价关中地区不同时间尺度的旱涝分布情况，然后根据提炼的不稳定度指标，定量地研究旱涝变化剧烈程度的时空分布及其变化规律。其中，在研究总体不稳定度时，采用的是各气象站1971-2007年月降水量的同期观测资料。

2.1 不同时间尺度旱涝不稳定度的分布规律

结合关中地区的降水特征[15]与当地工农业经济发展的需要，本研究选择了1，3，6，12个月共4个时间尺度。具体划分如下：1，3，12个月尺度时分别是以各月、各季和各年作为研究对象；6个月尺度时，分为湿润期5月到8月和干燥期9月到次年4月2个阶段。关中地区1971-2007年各月旱涝的不稳定度分布如表1所示。

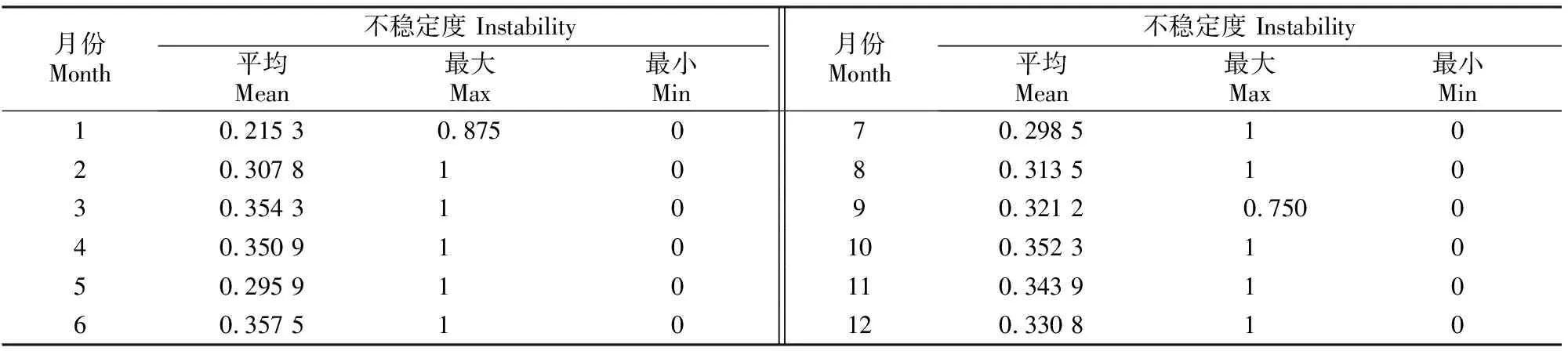
表 1 关中地区1971-2007年各月旱涝不稳定度的分布

由表1可以看出，1971-2007年各月旱涝的最小不稳定度均为0，说明各月的旱涝状态均会出现连续发生的情况，或者连续数月旱，或者连续数月涝，也或者连续数月正常，这与实际情况吻合。除1月和9月外，各月的最大不稳定度均是1，说明各月的旱涝状态均可能发生最大程度的变化，即会出现由某一状态发展成特旱或特涝的极端水情灾害事件；而在1月与9月，关中地区发生旱涝急剧变化的可能性很小。在各月中，6月的平均不稳定度最大，为0.357 5；1月的平均不稳定度最小，为0.215 3，说明6月旱涝的变化最不稳定，而1月旱涝的变化相对最稳定。

1971-2007年陕西关中地区不同时期旱涝不稳定度的分布如表2所示。

表 2 陕西关中地区1971-2007年不同时期旱涝不稳定度的分布

由表2可以看出，1971-2007年关中地区不同时期旱涝的最小不稳定度均为0，说明不同时期相邻2个时段的旱涝状态也会出现连续发生的情况。时间尺度为3个月时，春季和秋季的最大不稳定度相对较小，均为0.8，而夏冬两季的最大不稳定度均为1，说明春季和秋季旱涝变化的最大幅度相对较小，出现由某一状态发展成特旱或特涝的极端水情灾害事件的可能性较小。同时，冬季的平均不稳定度最大，夏季和秋季的平均不稳定度比较接近且相对较小，说明冬季旱涝的变化相对最不稳定，而夏季和秋季旱涝的变化比较稳定。时间尺度为6个月时，湿润期的最大不稳定度为0.8，而干燥期的最大不稳定度为1，说明在湿润期旱涝由某一状态发展成特旱或特涝的可能性很小，而在干燥期这种可能性则较大。另外，湿润期的平均不稳定度较干燥期小，因而湿润期旱涝的变化相对较为稳定。时间尺度为12个月时，年的旱涝最大不稳定度为1，说明年尺度下旱涝由某一状态发展成特旱或特涝的可能性较大。

此外，关中地区四季的平均降水量为：春季127.7 mm，夏季261.7 mm，秋季183.9 mm，冬季19.7 mm[15]。对比分析表2中平均不稳定度数据可知，在时间尺度为3个月和6个月时，时段内降水量越小，其旱涝的平均不稳定度越大，说明此时旱涝的平均不稳定度与降水量成反比，即时段内降水量越少，其旱涝变化越剧烈，这与实际情况相符。

2.2 不同时间尺度下旱涝不稳定度的变化规律

研究不同时间尺度下旱涝不稳定度沿时序的变化规律，有助于更加全面准确地分析旱涝的不稳定度对旱涝预测的影响。关中地区不同时期旱涝不稳定度的时序分布如图2和图3所示。

图 2 陕西关中地区1971-2007年不同季节旱涝不稳定度的时序分布

图 3 陕西关中地区1971-2007年不同时期旱涝不稳定度的时序分布

由图2和图3中不稳定度的分布折线及其拟合曲线可以看出，不同时期旱涝的不稳定度均呈现出一定的周期性变化特征。春季不稳定度在20世纪70年代中期、80年代初期和世纪之交等相对较大，夏季不稳定度在70年代中期、80年代初及90年代后期等相对较大，秋季不稳定度在80年代及21世纪初处于一个较高的峰值，冬季不稳定度在80年代前期以及90年代后期到21世纪初基本上都处于一个较高的峰值。湿润期不稳定度的周期变化特性相对明显，在80年代中期以及90年代中后期相对较大；干燥期不稳定度变化相对较大，在70年代中期、80年代初期、90年代中期及21世纪初均较大。年的旱涝不稳定度的周期变化特性也相对比较明显，在70年代中期、80年代中后期、90年代中期及21世纪初均相对较大。

由图2和图3中趋势线及其斜率(k)可以看出，在时间尺度为3个月时，春季和冬季不稳定度上升的趋势相对明显，夏季不稳定度的下降趋势较为明显，秋季不稳定度略微下降但基本持平，说明各时段内降水量越少，其旱涝不稳定度增大的速度越快；在时间尺度为6个月和12个月时，关中地区年的旱涝不稳定度均呈下降趋势，说明时间尺度较长者，其不稳定度逐渐减小。

由图2和图3中均方差(σ)和变差系数(Cv)可以看出，除了冬季以外，基本上时间尺度越长，其不稳定度的均方差越大，即不稳定度变化越剧烈。在时间尺度为3个月时，冬季不稳定度的均方差最大，而夏季不稳定度的变差系数最大，说明冬季不稳定度的绝对变化最剧烈，而夏季不稳定度的相对变化最剧烈。在时间尺度为6个月时，干燥期不稳定度的绝对变化更为剧烈，而其相对变化则更趋稳定。

2.3 不同时间尺度下旱涝平均不稳定度的空间分布规律

研究某一地区不同时间尺度下旱涝不稳定度的变化，有助于预测该地区不同时间尺度下旱涝的空间分布情况。本研究选取关中地区1971-2007年3，6，12个月时间尺度下旱涝平均不稳定度的空间分布情况(图4)予以说明。

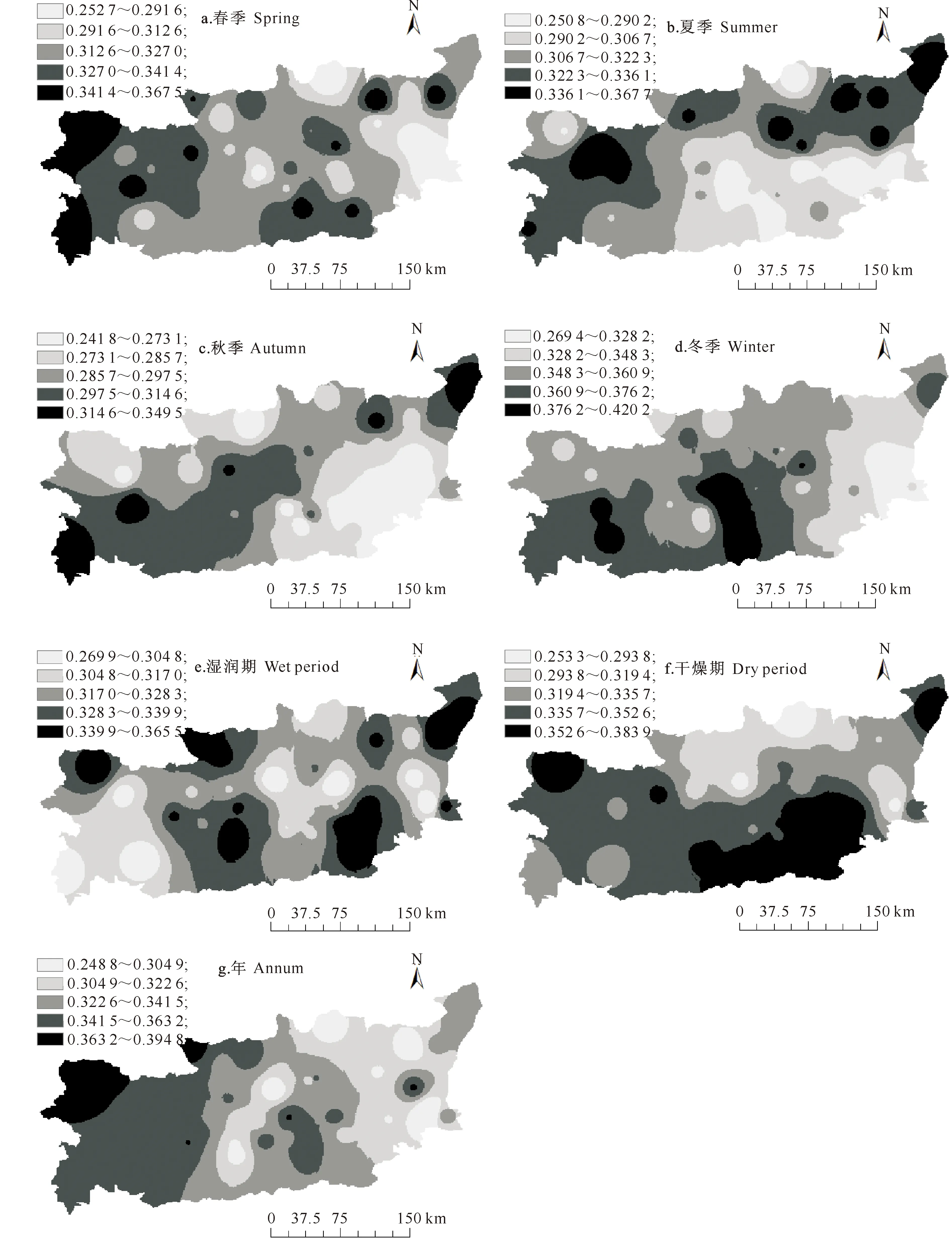
图 4 陕西关中地区1971-2007年不同季节和时期旱涝平均不稳定度的空间分布

由图4-a可以看出，春季平均不稳定度在陇县、凤县、宝鸡、合阳、白水、周至、蓝田及麟游等地最大，而在潼关-华阴-大荔一带、宜君及礼泉等地最小。由图4-b可以看出，韩城、澄城、白水、大荔、铜川-耀县及千阳-凤翔一带等夏季的平均不稳定度最大，而华阴-华县-渭南-高陵一带、宜君以及长安-咸阳-兴平-礼泉一带等地夏季的平均不稳定度最小。由图4-c可以看出，秋季平均不稳定度最大的地区有韩城、白水、宝鸡和凤县等，而秋季平均不稳定度最小地区包括关中东南部、旬邑、千阳、长安及咸阳等。由图4-d可以看出，户县-兴平-礼泉-乾县及宝鸡-太白一带等地冬季的平均不稳定度最大，而关中东南部地区冬季的平均不稳定度最小。由图4-e可以看出，湿润期的平均不稳定度在韩城-合阳、蓝田-临潼-渭南、长武-彬县、陇县以及周至-武功等地最大，而在凤县、太白、千阳、淳化、富平、大荔及华阴等地最小。由图4-f可以看出，关中东南部-南部、韩城、陇县及麟游等地干燥期的平均不稳定度最大，而在宜君、淳化及华阴等地干燥期的平均不稳定度最小。由图4-g可以看出，年的旱涝平均不稳定度最大的地区包括关中西北部及长武等地区，而年的旱涝平均不稳定度最小的地区有华阴、澄城、宜君、淳化及周至-武功一带等。此外，由图3还可以看出，同一时间尺度下，冬季和干燥期的平均不稳定度空间变异性相对较小。

2.4 不同时间尺度下旱涝不稳定度变化趋势的空间分布规律

了解不同时间尺度下旱涝不稳定度变化趋势的空间分布规律，对于更好地预测旱涝具有重要的意义。关中地区不同时期旱涝不稳定度变化趋势的空间分布如图5和图6所示。

图 5 陕西关中地区1971-2007年不同季节旱涝不稳定度变化趋势的空间分布

由图5-a可以看出，关中的中部地区、韩城-合阳-澄城一带及陇县等地春季旱涝不稳定度有所增大，其中旬邑-淳化-泾阳一带、高陵以及眉县等地增大的速度最快，而千阳-宝鸡一带及华阴等地是关中地区春季不稳定度减小速度最快的地区。由图5-b可以看出，关中大部分地区夏季不稳定度呈减小趋势，其中千阳-宝鸡-岐山-眉县一带、宜君以及泾阳等地减小速度最快，而只有合阳、渭南、高陵、礼泉、户县及华阴等少部分地区夏季不稳定度是增大的。由图5-c可以看出，秋季不稳定度在关中东部-北部-西北部及周至-武功-眉县等地是减小的，其中关中东部、旬邑-彬县-永寿-乾县一带及陇县等地减小速度最快，而太白等地秋季不稳定度增大最快。由图5-d可以看出，除了关中西北部、周至-武功-眉县-永寿一带、白水-蒲城及韩城等地冬季不稳定度减小以外，关中其他地区冬季不稳定度均呈增大趋势，其中蓝田-临潼-渭南-高陵一带、泾阳-咸阳及旬邑等地增大的速度最快。

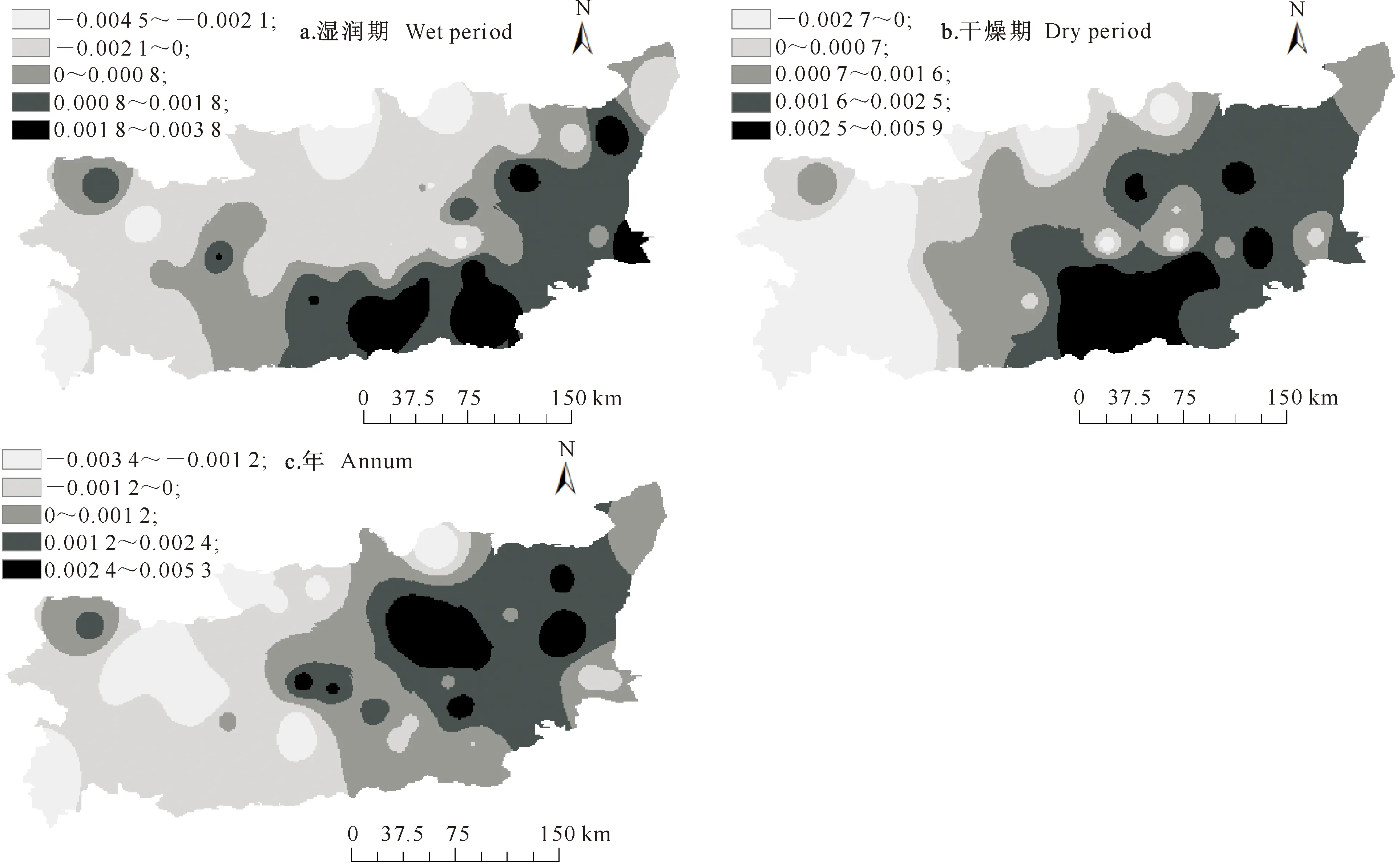
图 6 陕西关中地区1971-2007年不同时期旱涝不稳定度变化趋势的空间分布

由图6-a可以看出，湿润期不稳定度减小的地区主要包括关中北部、西部等，其中宜君、旬邑、千阳、凤县等地减小速度最快，而合阳、蒲城、潼关、蓝田-临潼及户县-长安-西安等地湿润期不稳定度增大速度最快。由图6-b可以看出，关中除了西部、西南部、长武、旬邑、宜君等少部分地区以外，其他大部分地区干燥期不稳定度均有所增大，其中关中南部、华县、蒲城及铜川-耀县等地增大的速度最快。由图6-c可以看出，关中西部、南部、北部等地年的不稳定度均呈减小趋势，其中宜君、旬邑、长武-彬县、千阳-凤翔-岐山、周至-武功以及凤县等地减小速度最快，而澄城、大荔、铜川-耀县-富平、临潼、乾县、礼泉等地年的不稳定度增大速度最快。

2.5 不同时间尺度下旱涝不稳定度的均方差空间分布规律

均方差反映了一个系列的波动程度，分析关中地区不同时间尺度下旱涝不稳定度的均方差的空间分布(图7)规律，是研究不同时间尺度下旱涝不稳定度波动规律的关键。

由图7-a可以看出，白水-澄城-大荔-华阴一带、宜君、长武、彬县及凤县等地春季旱涝不稳定度的波动最小，而西安-高陵-泾阳、铜川、旬邑、永寿、岐山、宝鸡等地春季不稳定度的波动最大。由图7-b可以看出，夏季不稳定度在陇县、长武、户县、咸阳、高陵-临潼及华阴等地区波动最小，而在扶风-乾县-永寿、泾阳、铜川-耀县等地波动最大。由图7-c可以看出，秋季不稳定度波动最小的地区主要有长武、旬邑、韩城、凤县、太白、礼泉-武功-兴平-咸阳-户县、华县-渭南-临潼-蓝田以及华阴等，而波动最大的地区主要包括潼关、合阳、高陵、岐山及宝鸡等。由图7-d可以看出，冬季不稳定度在合阳、华阴以及关中的中西部地区等波动最小，而在韩城、白水-蒲城、富平、泾阳、陇县及宜君-旬邑-长武一带波动最大。由图7-e可以看出，华阴、渭南及凤县等地湿润期不稳定度的波动最小，而韩城、澄城、白水-蒲城、蓝田、西安-长安、彬县-永寿-乾县-礼泉-武功、凤翔及陇县等湿润期不稳定度的波动最大。由图7-f可以看出，干燥期不稳定度在华阴、宜君及淳化等地波动最小，而在韩城、咸阳-户县及周至等地波动最大。由图7-g可以看出，年的旱涝不稳定度波动最小的地区主要包括凤县、太白、岐山-眉县、周至、户县、淳化、蓝田及华阴等地，而年的旱涝不稳定度波动最大的地区主要有关中东北部、潼关、蒲城及咸阳等地。

图 7 陕西关中地区1971-2007年不同季节和时期旱涝不稳定度的均方差空间分布

3 结 论

本研究以陕西关中地区为例，对不同时间尺度下旱涝变化的剧烈程度进行了定量化分析，根据提炼出的不稳定度这一评价指标，着重探讨了关中地区不同时间尺度下旱涝不稳定度的时空分布及其变化规律。得出以下结论：将旱涝不稳定度与SPI指标结合起来应用，能够有效地反映出不同时间尺度下旱涝变化的剧烈程度。根据旱涝不稳定度的判定，可知关中地区不同时间尺度下旱涝状态均会出现连续发生的情况；关中地区在时间尺度为3个月和6个月时，时段内降水量越少，其旱涝的平均不稳定度越大，即旱涝的平均不稳定度与降水量成反比。关中地区不同时期旱涝的不稳定度均呈现出一定的周期性变化特征，且基本上时间尺度越长，不稳定度的均方差越大，即不稳定度波动越大。在时间尺度为6个月和12个月时，关中地区的旱涝不稳定度均逐渐减小。在同一时间尺度下，冬季和干燥期的旱涝平均不稳定度的空间变异性均相对较小。

此外，本研究定量地分析了关中地区旱涝变化剧烈程度的时空分布及其变化规律，得到了一些结果，这对该地区的旱涝预测、防灾减灾以及水资源合理规划与利用等具有一定的指导意义。但鉴于不稳定度这一指标还处于初步研究阶段，难免存在不足之处，如不稳定度的分布具有怎样的特征，如何将不稳定度应用于旱涝预测以提高预测精度等，这些问题都还有待进一步地深入研究。

[参考文献]

[1] 赵 丽，冯宝平，张书花.国内外干旱及干旱指标研究进展 [J].江苏农业科学，2012，40(8)：345-348.

Zhao L,Feng B P,Zhang S H.The research progress of dro-ught and drought index at home and abroad [J].Jiangsu Agricultural Science,2012,40(8):345-348.(in Chinese)

[2] Sönmez F K,Kömüscü A Ü,Erkan A,et al.An analysis of spatial and temporal dimension of drought vulnerability in Turkey using the Standardized Precipitation Index [J].Natural Hazards,2005,35:243-264.

[3] Richard R H J.A review of twentieth-century drought indices used in the United States [J].Bulletin of American Meteorological Society,2002,83(8):1149-1165.

[4] Bonaccorso B,Bordi I,Cancelliere A,et al.Spatial variability of drought:An analysis of the SPI in Sicily [J].Water Resources Management,2003,17:273-296.

[5] Logan K E,Brunsell N A,Jones A R,et al.Assessing spatiotemporal variability of drought in the U S central plains [J].Journal of Arid Environments,2010,74:247-255.

[6] Tsakiris G,Vangelis H.Towards a drought watch system bas-ed on spatial SPI [J].Water Resources Management,2004,18:1-12.

[7] Hayes M J,Svoboda M,Wilhite D A,et al.Monitoring the 1996 drought using the SPI [J].Bull Amer Meteor Soc,1999,80:429-438.

[8] Caccamo G,Chisholm L A,Bradstock R A,et al.Assessing the sensitivity of MODIS to monitor drought in high biomass ecosystems [J].Remote Sensing of Environment,2011,115:2626-2639.

[9] Shahabfar A,Ghulamb A,Eitzinger J.Drought monitoring in Iran using the perpendicular drought indices [J].International Journal of Applied Earth Observation and Geoinformation,2012,18:119-127.

[10] 司昌亮，卢文喜，王喜华.基于干旱指数法的星星哨灌区旱涝状况研究 [J].节水灌溉，2012(6)：44-48.

Si C L,Lu W X,Wang X H.Study on drought and waterlog condition of xingxingshao irrigation district base on index method [J].Water Saving Irrigation,2012(6):44-48.(in Chinese)

[11] 邵 进，李 毅，宋松柏.基于SPI模型的江汉平原旱涝分布及其变化规律的研究 [J].水文，2012，32(2)：34-39.

Shao J,Li Y,Song S B.Distribution and variation law of drought/waterlog in Jianghan Plain based on SPI [J].Journal of China Hydrology,2012, 32(2):34-39.(in Chinese)

[12] 白永清，智协飞，祁海霞，等.基于多尺度SPI的中国南方大旱监测 [J].气象科学，2010，30(3)：292-300.

Bai Y Q,Zhi X F,Qi H X,et al.Severe drought monitoring in south China based on the standardized precipitation index at different scales [J].Scientia Meteorologic Sinica,2010,30(3):292-300.(in Chinese)

[13] Gebrehiwot T,Veen A V D,Maathuis B.Spatial and temporal assessment of drought in the Northern highlands of Ethiopia [J].International Journal of Applied Earth Observation and Geoinformation,2011,13:309-321.

[14] Khan S,Gabriel H F,Rana T.Standard precipitation index to track drought and assess impact of rainfall on watertables in irrigation areas [J].Irrig Drainage Syst,2008,22:159-177.

[15] 宋进喜，宋令勇，惠泱河，等.陕西省降水时空变化特征及资源化研究 [J].北京师范大学学报：自然科学版，2009，45(5/6)：575-581.

Song J X,Song L Y,Hui Y H,et al.Spatio-temporal variation and utilization of precipitation in Shaanxi Province [J].Journal of Beijing Normal University:Natural Science,2009,45(5/6):575-581.(in Chinese)