连续波状横峰对ZrO2陶瓷材料润滑性能的影响*

2022-01-19赵金玲崔金磊

润滑与密封 2021年12期

赵金玲崔金磊王静

(1.青岛理工大学机械与汽车工程学院山东青岛 266520；2.东华大学机械工程学院上海 201620)

随着科学技术的进步与发展，具有高硬度、高强度、耐磨损、耐高温、耐腐蚀的高性能陶瓷材料已被广泛应用到诸多高新技术领域[1]，如工程陶瓷轴承已成功地运用到航空发动机、高速客车以及精密机床等的主轴上[2]。如今，如何改善陶瓷材料的摩擦学性能，进一步提高其使用寿命是人们所重点关心的问题。研究表明，在接触副表面设计出一定形貌的表面纹理(如表面粗糙度、微凹坑、沟槽等)可有效提高其摩擦学性能[3-4]。

早在20世60年代，HAMILTON等[5]就提出可利用表面微凸起产生的附加动压润滑效应来改善摩擦学性能。因为凸起的一边与摩擦副的另一面之间形成收敛楔会产生流体动压力，而凸起的另一边的发散楔产生的负压由于气穴的产生得到了限制，最终为相对滑动表面产生额外承载力，而达到降低摩擦因数的目的。近年来，许多学者对表面形貌改善摩擦学性能的研究做了大量工作。田园等人[6]利用原位成型方法制得了表面微织构陶瓷材料，对此材料进行摩擦磨损试验，发现沟槽型纹理试样的摩擦因数较为平稳，且与无织构试样相比，最大、最小摩擦因数分别减少了约33.3%和18.2%。鲍雨梅等[7]采用激光技术在等离子喷涂 HA/ZrO2生物涂层表面制备了圆形和椭圆形表面织构形貌，发现一定参数的织构阵列，可有效减小摩擦因数，且长轴平行于上表面运动方向的椭圆形织构能产生更多的承载力，具有更优的减摩、抗磨效果。方媛等人[8]利用激光技术在Al2O3/Mo层状自润滑结构陶瓷表面制备了微坑型表面形貌，研究表明，微凹坑特殊的结构特征和集成固体润滑剂优异的减摩抗磨性能能使氧化铝/钼复合陶瓷在室温、中温区域的摩擦学性能得到显著改善，可实现材料在较宽温度范围内的连续润滑。邢佑强[9]通过实验和理论研究了多尺度微织构陶瓷刀具表面的摩擦磨损性能，发现在干摩擦条件下，微织构可减小试样表面的磨粒磨损和黏结。张记云[10]对不同形貌的微织构自润滑陶瓷刀具进行切削试验，发现与无织构刀具相比，具有横向纹理的陶瓷刀具具有良好的切削性能。以上关于表面形貌改善陶瓷材料摩擦学性能的研究多集中在实验方面，且多为面接触的混合润滑或干摩擦状态，对于点接触热弹流全膜润滑数值模拟陶瓷表面纹理的研究还比较少见。

基于此，本文作者以氧化锆(ZrO2)陶瓷材料与钢材(Steel)组成的点接触副为研究对象，在两固体表面分别设计出具有连续性的波状横峰，使用点接触瞬态非牛顿热弹流模型，通过数值模拟求解两表面的波状横峰互相追赶及超越过程中的相互作用及影响，同时分析横峰尺度和接触固体尺度对接触区润滑性能的影响，以期为工程设计提供参考。

1 数学模型

1.1 粗糙度函数及膜厚方程

设定两固体a、b表面各自具有连续波状横峰，粗糙度函数分别记为δa(x,t)和δb(x,t)，参考文献[11]中的粗糙度模型，则

Aa,b/2|x-(xi+ua,bt)+iLa,b|≤Ba,b,i=0,1,2,3…

(1)

式中：Aa,b、Ba,b、La,b分别为两固体表面横峰的高度、半宽和波长；ua,b为接触副表面速度；t为横峰进入接触区的时间；xi为初始时刻(t=0)首个横峰的中心位置。

为方便研究两表面横峰如何相互影响及作用，膜厚方程写为

h(x,y,t)=hb(x,y,t)-ha(x,y,t)

(2)

式中：ha和hb分别表示两接触固体a、b的膜厚方程，其表达式为

(3)

式中：E′为当量弹性模量；Ea、Eb分别为两固体表面的弹性模量；νa、νb分别为固体a、b的泊松比;Δ是两固体表面的弹性变形之和，

1.2 Reynolds方程

考虑时变效应的Reynolds方程[12]为

(4)

式中：p为流体压力；h为油膜厚度；ue= (ua+ub)/2为卷吸速度；Reynolds方程的边界条件及其他参数详见文献[13]。

1.3 黏压黏温方程

选用Ree-Eyring非牛顿流体[14]，其本构方程为

(5)

流体表观黏度[15]：

η=η0exp{(lnη0+9.67)×

(6)

1.4 密压密温方程

润滑油密度、压力和温度之间采用Dowson和Higginson回归经验公式[16]：

(7)

式中：ρ0为润滑油环境密度。

1.5 载荷平衡方程

外载荷w与油膜压力p在整个计算域上的平衡方程为

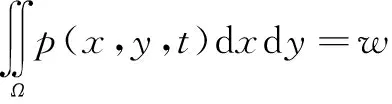
(8)

式中：w= 2πabpH/ 3；pH为最高接触压力；a、b分别为接触椭圆的短、长半径。

1.6 润滑油和两固体的能量方程

(9)

(10)

式中：c、ca,b分别为润滑油、两接触固体的比热容；k、ka,b分别为润滑油、两接触固体的热传导系数，边界条件同文献[13]。

1.7 摩擦因数

μ=(fa+fb)/(2w)

(11)

fa=-2∬τx|z=0dxdy；fb=-2∬τy|z=hdxdy

式中：fa、fb分别为固体a、b表面的摩擦力。

2 数值方法

文中选用两接触副为光滑表面时的稳态解为算例初始条件，对于全部算例，氧化锆陶瓷及钢材表面上连续横峰的首个横峰的初始位置分别为Xa=-11.6，Xb=- 2.9，计算域取Xin=-3.6，Xout=1.52，Yin=-3.2，Yout=3.2。弹性变形求解采用多重网格积分法，压力求解采用多重网格法，网格层数采用5层，最高层网格共有513×129个节点。两固体热层厚2.5a，设Z方向上油膜内的温度节点n=16，两固体的温度节点nza=nzb=8。时间间隔Δt=0.01，连续横峰首次在接触区X=0处相遇共经历725个瞬时。定义每个瞬时压力、温度及载荷的相对误差分别为ERRP、ERRW和ERRT，直到ERRP<10-4、ERRW<10-5、ERRT<10-4时迭代终止。

3 输入参数

表1 接触固体及润滑油的参数(T0=303 K)Table 1 Properties of contact bodies and oil(T0=303 K)

4 结果和讨论

4.1 接触副材料的影响

为明晰陶瓷材料对润滑特性的影响，先将ZrO2-Steel与Steel-Steel接触副在理想光滑条件下膜厚和温度场的异同进行对比。前期研究[17]表明，对于ZrO2-Steel接触副，ZrO2为快速运动表面时接触区会得到更厚的弹流油膜。文献[18-19]中也证实，接触材料的热导率对EHL机制中的摩擦学行为有非常重要的影响，即当高速表面的导热系数小于低速表面时会得到更厚的膜厚、更大的压力和更高的油膜温度，且摩擦因数也会小于低速表面使用低导热系数的情况。所以文中设定氧化锆为快速运动表面，钢材为慢速表面，且固定接触半径R=0.04 m。

图1所示为滑滚比Σ=1.2时两组接触副在XOZ截面上的膜厚分布曲线。可知，ZrO2-Steel接触区内的平均膜厚可达到1.4 μm左右，而对于Steel-Steel接触副，平均膜厚只有1.1 μm左右，比前者减小约20%。

图1 两组接触副在XOZ截面上的膜厚分布曲线Fig 1 Film thickness distribution curves on XOZ cross-sections for two different contact pairs

为解释这种差异，图2给出了上述2种接触副在对称平面上X= 0列润滑油流速分布情况。可见ZrO2-Steel接触副润滑油的流速明显比Steel-Steel接触副慢，为维持流量守恒，前者的平均膜厚必然大于后者[17]。

图2 两组接触副在对称平面上X=0列润滑油流速分布情况Fig 2 Flow distribution curves of lubricant at column X=0 on the symmetry plane for two different contact pairs

流速的差异又源于陶瓷材料的热学特性导致的接触区温度场的不同。图3给出了与图1及图2对应的两组接触副在XOZ截面上的温度等值线图，纵坐标代表膜厚方向，z/h=0对应快速表面，z/h=1为慢速表面。因此图3(a)中氧化锆陶瓷为下表面，钢材为上表面。

由图3可知，ZrO2-Steel接触区内会有更高的油膜温度，且图3(a)中最高温度约在z/h=0.3处，即更靠近氧化锆陶瓷表面。而图3(b)所示的Steel-Steel接触副，油膜的最高温度稍靠近慢速表面，约在z/h=0.58处。原因在于氧化锆的热传导系数很小，传热困难。图3(a)中尽管氧化锆为快速表面经由对流带走的热量较慢速表面更多，但显然此时热传导起了主导的作用。图3(b)中因两表面材料相同，温度差异主要是由对流作用造成。温度场的差异，会导致润滑剂黏度的不同，进而影响接触区内润滑油流速，最终导致平均膜厚的差异，如图1所示。

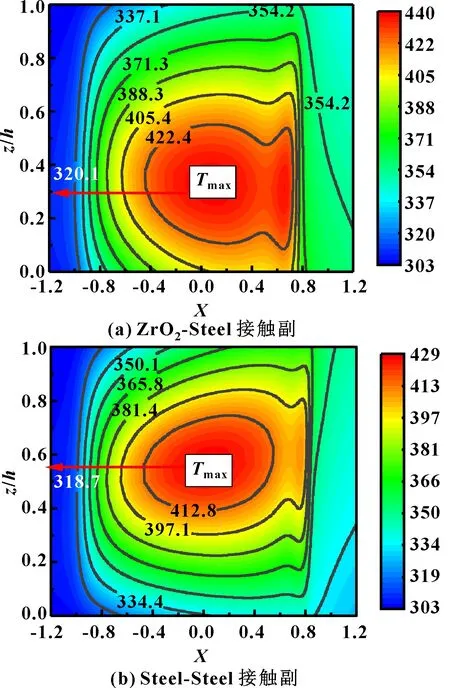
图3 两组接触副在XOZ截面上的温度等值线图Fig 3 Temperature contour plots on XOZ cross-sections for two different contact pairs (a) ZrO2-Steel contact pair;(b) Steel-Steel contact pair

文中以下关于表面连续波状横峰对ZrO2-Steel接触副的讨论，亦将氧化锆陶瓷始终作为快速表面。

4.2 连续横峰的瞬态效应

同样固定接触半径R=0.04 m，则接触椭圆短半径a=0.654 mm，对于光滑接触表面情况，由4.1小节数值计算得hcen=1.362 μm，hmin=0.649 μm。

在ZrO2-Steel接触副两固体表面分别设计连续波状横峰形貌，且设定横峰的高度Aa,b=0.69 μm，半宽Ba,b=62 μm，相邻横峰间的波长La,b=248 μm。

基于点接触瞬态非牛顿热弹流润滑模型，图4给出了连续波状横峰进入接触区后4个典型时刻(N=725、995、1 002、1 008)XOZ截面上两接触表面的膜厚及压力分布情况。如图4(a)所示，当N=725时，接触副两表面的首对横峰在接触区X=0处相遇，虽然两横峰的高度和Aa+Ab=1.38 μm，已超过光滑情况时两表面间的膜厚值1.362 μm，但接触区仍可保持全膜润滑状态。之后，陶瓷表面上的横峰会逐渐赶超钢材表面上的横峰，两峰交错，将在压力曲线上各自产生一个局部高压，如图4(b)所示，相较于图4(a)发现两表面横峰的高度有所增加。随着陶瓷表面的横峰继续向钢材表面上的另一横峰靠近，两横峰所引起的局部高压开始互相干涉、融合，直至完全叠加，如图4(c)、(d)所示，表现在压力曲线上发现其峰值明显增大。反过来，如此高的压力峰又会在接触表面上产生很大的弹性变形，使两表面的横峰被压低压平，致使其高度明显降低。可见，两接触副表面的连续横峰在运动过程中会存在瞬态效应，从而引起压力和油膜的扰动现象，其过程大致重复图4(a)—(d)。

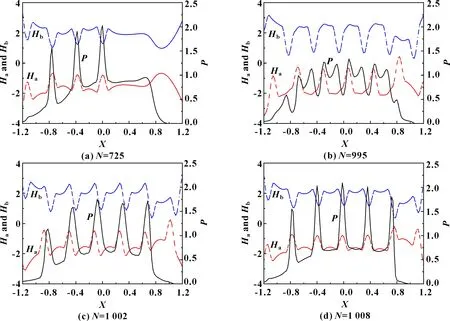
图4 ZrO2-Steel接触副两表面皆有横向波状凸峰时4个典型时刻XOZ截面上的压力和膜厚分布Fig 4 Pressure and film thickness distribution on the XOZ section at four instants when both surfaces of the ZrO2-Steel contact pair have wavy transverse ridges(a) N=725;(b)N=995;(c)N=1 002;(d)N=1 008

图5(a)、(b)对应图4(b)、(d)两典型时刻XOZ截面上的温度分布。由图5可知，油膜中层及接触副两表面的温度Tm、Ta、Tb的变化趋势大致和图4中的压力曲线相似，即在横峰的中心位置会出现温度峰值，且油膜中层的温度Tm最高，陶瓷表面的温度Ta次之，而钢材表面的温度Tb最低。通常接触副中的快速表面会因对流作用带走更多的热量，而表现出较低的温度，但氧化锆陶瓷(ZrO2)材料的导热率仅有3 W/(m·K)，还不足钢材(Steel)的1/15，从而导致其表面传热困难(近乎绝热)，而运动慢的钢材却因良好的热传导性使其表面温度达到了最低。

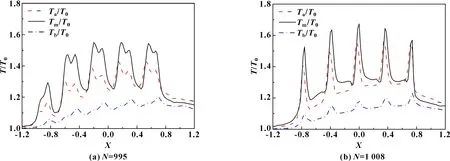
图5 ZrO2-Steel接触副两表面皆有横向波状凸峰时2个典型时刻XOZ截面上的温度分布Fig 5 Temperature distribution on the XOZ section at two instants when both surfaces of the ZrO2-Steel contact pair have wavy transverse ridges (a)N=995;(b)N=1008

4.3 波长的干涉效应

文中将主要分2种情况进一步讨论连续横峰的波长L对ZrO2-Steel接触副润滑状态的影响(1)陶瓷和钢材表面分别设定3种等波长连续横峰形貌；(2)陶瓷和钢材表面设定2种不等波长连续横峰形貌。

图6给出了整个接触区都已被连续横峰所覆盖，且两接触副表面横峰波长La,b分别为165、248、330 μm时摩擦因数μ及最小油膜厚度hmin随时间的变化情况。由图6(a)可知，摩擦因数值会在一定范围内来回波动，且波长越短，波动频率越高，波动幅度越大，反之亦然。具体以La,b=248 μm为例，其摩擦因数μ在0.011 3～0.013 7之间来回波动，同工况下理想光滑表面的摩擦因数值为0.013 7，说明在接触副表面设计出连续波状横峰在全膜润滑时可起到降低摩擦因数的作用，这与CHANG[11]在1992年研究的Steel-Steel线接触副两表面粗糙度对弹性流体动力润滑影响的结论是一致的，即在全膜润滑状态下，线接触副两表面的粗糙度随接触副的相对运动和相互作用会起到降低摩擦因数，改善摩擦学性能的目的。图6(b)表明，最小油膜厚度同样遵循上述变化规律，且与摩擦因数成反对称关系，即最小膜厚越厚，摩擦因数越小。

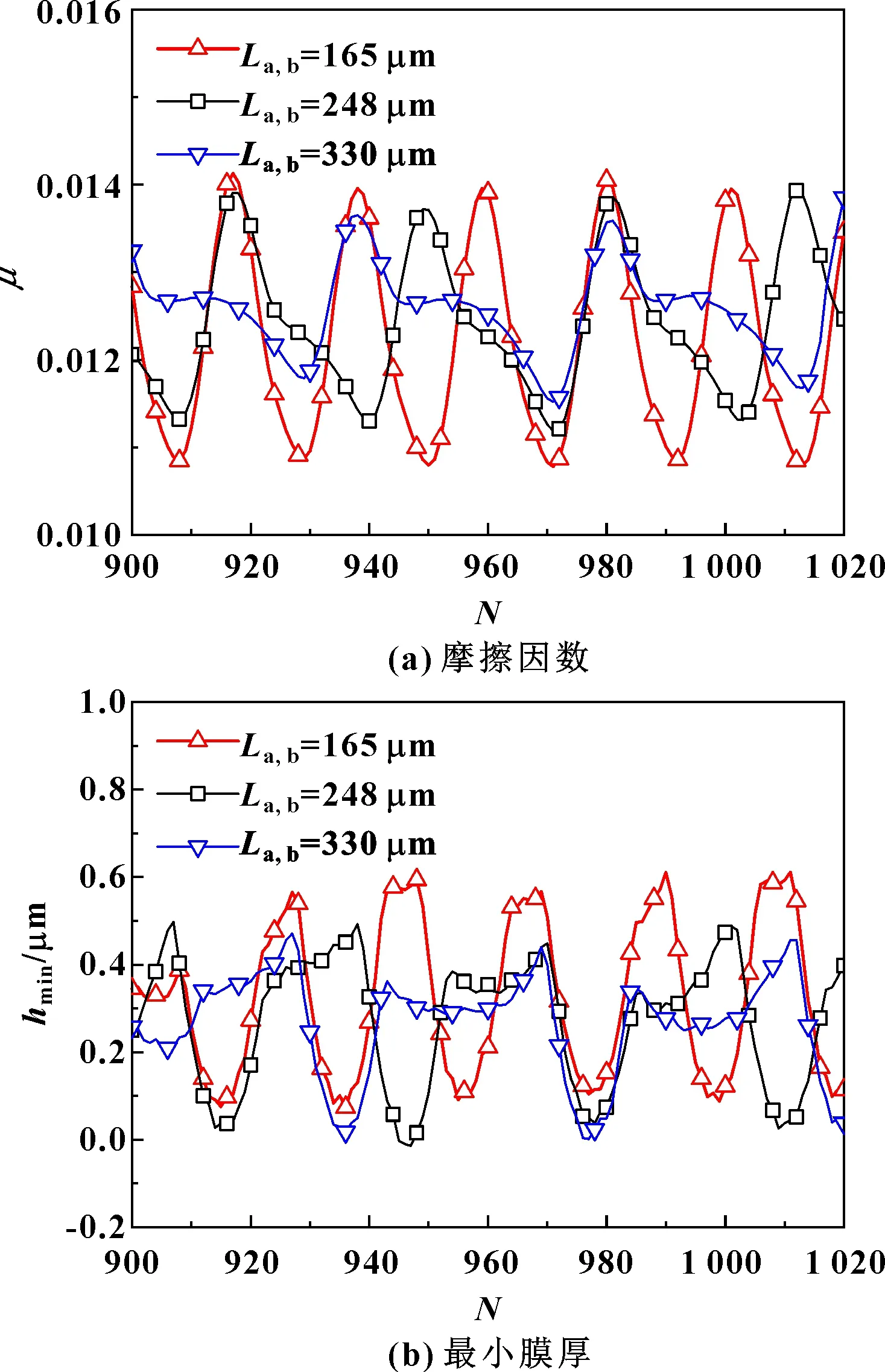
图6 ZrO2-Steel接触副两表面具有相同粗糙形貌时摩擦因数和最小膜厚随时间的变化曲线Fig 6 Time variation curves of friction coefficient (a) and minimum film thickness (b) when the ridges of two surfaces of ZrO2-Steel contact pair have the same wavelengths

图7给出了固定钢材表面的横峰波长Lb为248 μm不变，在氧化锆陶瓷表面分别设定165、330 μm 2种不同波长时摩擦因数μ随时间的变化情况。对于两接触副表面粗糙形貌不同的情况，其相近的横峰相互作用发生在不同时刻，两接触副表面的横峰几乎很难相遇。由图7可知，摩擦因数仍在一定范围内来回波动，只是相较于图6(a)两表面粗糙形貌相等的情况，其摩擦因数的变化范围明显减小了，且波动不再遵循来回往复的规律性变化，而是变得没有规律可循。同时，此情况下，当陶瓷表面的波长La小于钢材表面波长Lb时会得到更小的摩擦因数值。

图7 ZrO2-Steel接触副两表面具有不同粗糙形貌时摩擦因数随时间的变化曲线Fig 7 Time variation curves of friction coefficient with time when the ridges of two surfaces of ZrO2-Steel contact pair have different wavelengths

4.4 接触区及连续横峰的尺度效应

表2 不同尺度R下的理想光滑表面稳态解结果Table 2 The steady-state solutions of ideal smooth surfaces under different scales R

对于文中所有算例都设定Hertz压力pH=1 GPa，由表2可知，Hertz接触半径a会随R的增大而增大，且保持正比关系，因此，后面讨论的尺度效应要保证各横峰参数与曲率半径R成正比关系，详见表3。

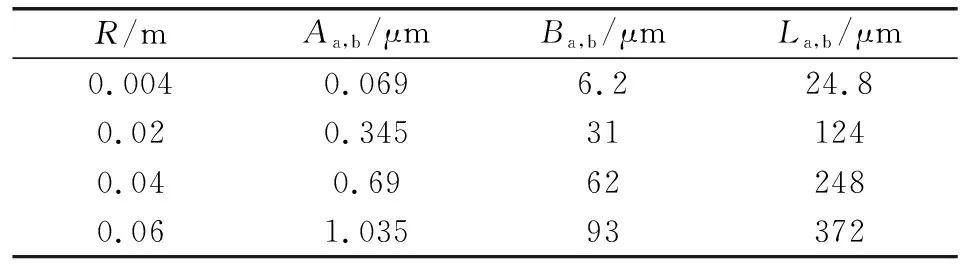
表3 不同尺度参数R对应的横峰参数Table 3 The ridge size corresponding to different R

按照表3所示的尺度进行数值求解，将R=0.004和0.06 m在N=1 008时刻的压力、膜厚以及两固体表面和油膜中层的温度绘于图8中。

图8 尺度R对ZrO2-Steel接触副XOZ截面上膜厚、压力及温度的影响(N=1 008)Fig 8 Effect of R on film thickness,pressure and temperature distributions at N=1 008 (a) R=0.004 m;(b) R=0.06 m

由图8可知，两尺度下连续横峰所引起的量纲一压力和膜厚差别不大，但温度曲线却变化明显，即曲率半径R=0.06 m所对应的接触区内各温度明显要高于R=0.004 m的情况。另外，大尺度下油膜中层与两固体表面间的温度差要明显大于小尺度的情况。造成此现象的原因是，曲率半径R越大两表面速度差越大(Δu=ua-ub=1.2ue，参考表2)，因此，大尺度下剪切发热量会更多。同时，小尺度R=0.004 m的膜厚很小，这使油膜内部的热量会很快通过接触副表面传出接触区，进而导致三条曲线差别较小。另外，入口区(X<-1)温度也会随曲率半径R的增大而有所增大。

该结论与文献[20]中研究的尺度效应对滚滑工况下弹性流体动力润滑的影响具有一致性，即尺度效应对热弹流动力润滑性能的影响非常显著。当接触区尺寸改变时，剪切热将成为影响油膜温度最重要的因素，当接触区尺度足够大时，Eyring流体的有效黏度几乎与牛顿流体的有效黏度相同，此时可忽略非牛顿效应，尺度效应将占主导地位；反之，当接触区尺度足够小时，可忽略尺度效应。

为进一步分析不同尺度R对ZrO2-Steel接触副润滑状态的影响，图9给出了N=1 008时刻四组不同接触尺度(R=0.004、0.02、0.04、0.06 m)下所对应的摩擦因数、中心膜厚以及最小膜厚值。可知，中心膜厚hcen和最小膜厚hmin均随曲率半径R的增大而增大，但最小膜厚的增长趋势很缓，在R为0.02～0.06 m的范围内几乎没有太大变化，而摩擦因数μ却随曲率半径R的增大呈不断减小趋势。

图9 ZrO2-Steel接触副不同尺度下最小膜厚、中心膜厚和摩擦因数变化情况(N=1 008)Fig 9 Comparisons of friction coefficient,minimum film thickness and central film thickness of ZrO2-Steel contact pair under different scales(N=1 008)