滑板上表面由不同材料组合的板块模型分类剖析
2022-01-19广东吴炳光
广东 吴炳光
滑块和滑板叠加的模型简称为“板块模型”,这两个简单的“道具”为考查学生的物质观念、运动与相互作用观念、能量观念展现了丰富多彩的情境,是高中物理讲、学、练、测的重要模型之一。
在常见的习题、试题等案例中,“板块模型”的滑板上表面通常是由同一种材料构成的,要么是光滑的平面,要么就是动摩擦因数为一个恒定数值的粗糙平面,情境比较单一,缺少复杂性和新颖性。如果在“板块模型”的滑板上表面做文章,将其设置为由几种不同材料分阶段组合,通过学生对多过程问题的解答,可以比较准确地反映学生分析问题、解决问题的能力和学科核心素养。下面通过创设类型多样的、具有一定复杂程度的试题,对滑板上表面由不同材料组合的“板块模型”进行分类剖析,供大家参考。
一、滑板上表面是“粗糙+光滑”两段组合
【例1】如图1所示,质量M=3 kg的滑板A置于粗糙的水平地面上,A与地面的动摩擦因数μ1=0.3,其上表面右侧光滑段长度L1=2 m,左侧粗糙段长度为L2,质量m=2 kg且可视为质点的滑块B静止在滑板上的右端,滑块与滑板上表面粗糙段的动摩擦因数μ2=0.15,取g=10 m/s2,现用F=18 N 的水平恒力拉动A向右运动,当A、B分离时,B相对地面的速度vB=1 m/s,求滑板粗糙段长度L2的大小。

图1
【解析】在F的作用下,滑板A做匀加速直线运动,滑块B静止不动。
当A运动位移为L1时B进入粗糙段,设此时A的速度为vA。
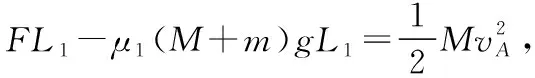
当滑块B由光滑段进入粗糙段后,设滑板A的加速度为aA,滑块B的加速度为aB。
对滑板A,由牛顿第二定律得F-μ1(M+m)g-μ2mg=MaA;解得aA=0
对滑块B,由牛顿第二定律得μ2mg=maB;解得aB=1.5 m/s2
这就说明,滑板A以vA=2 m/s的速度做匀速直线运动直至A、B分离。
设滑块B在粗糙段滑行的时间为t。
对滑板A有sA=vAt
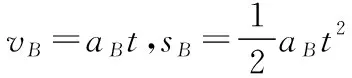
所以,滑板粗糙段长度L2=sA-sB=1 m
【点评】这道试题,滑板上表面由“粗糙+光滑”两段组合,滑块B开始处于光滑段,滑板A先做匀加速运动,当滑块B由光滑段进入粗糙段后,滑板A将做什么性质的运动呢?这就需要将整体法、隔离法、牛顿运动定律、相对运动等重要内容紧密结合,通过定量计算,才能知道滑板A第二阶段做匀速直线运动直至A、B分离。这种多过程的情境设计,可以帮助学生更好地形成“运动与相互作用观念”,对学生综合解题能力的培养有显著的作用。
二、滑板上表面是“粗糙+光滑+粗糙”三段组合
【例2】如图2所示,长度L=7 m、质量M=1 kg的滑板C静止在粗糙的水平地面上,滑板上表面左右两端各有长度d=1 m的粗糙区域,中间部分光滑。可视为质点的小物块A和B初始时如图放置,质量分别是mA=0.25 kg和mB=0.75 kg,A、B与滑板粗糙区域之间的动摩擦因数均为μ1=0.2,滑板与水平地面之间的动摩擦因数为μ2=0.3。某时刻对滑板施加F=8 N的水平恒力,滑板开始向右加速,A与B碰撞瞬间粘在一起不再分开并撤去F,取g=10 m/s2,求:
(1)物块A与B碰后瞬间的速度大小;
(2)最终物块A与滑板C左端的距离。

图2
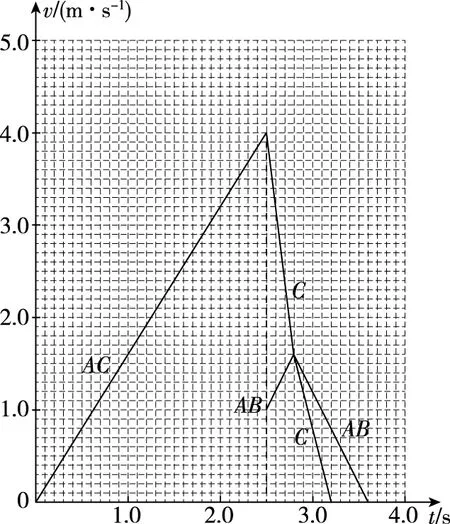
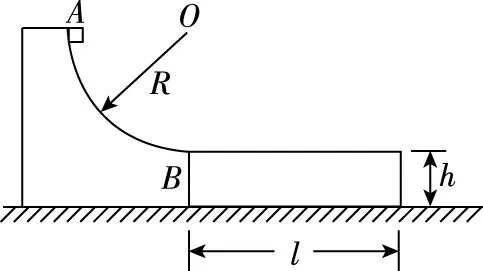
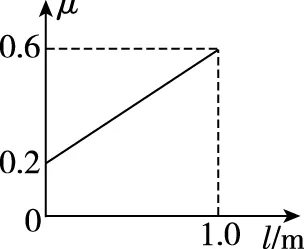
【解析】(1)假设物块A与滑板C共同加速,加速度为a。对物块A与滑板C,由牛顿第二定律得F-μ2(M+mA+mB)g=(M+mA)a;而当C对A的摩擦力达到最大静摩擦力时,设A的加速度为aA。对物块A,由牛顿第二定律得μ1mAg=mAaA;联立各式解得a=1.6 m/s2,aA=2 m/s2;由于a (2)撤去力F后,物块AB整体继续做匀加速直线运动,设加速度为a1;对物块AB整体,由牛顿第二定律得μ1(mA+mB)g=(mA+mB)a1;滑板C做匀减速直线运动,设加速度大小为a2;对滑板C,由牛顿第二定律得μ2(M+mA+mB)g+μ1(mA+mB)g=Ma2。 图3 另外,还可以应用v-t图像法解答此题,过程更直观,临界情况更明确,如图3所示。需要强调的是,用v-t图像法解答的过程中,必须判断说明AB整体不会向右滑过C滑板左边粗糙区域。主要思路如下: AB碰后一直到A、B、C均停止运动过程,有: 最终AB整体与滑板左端的水平距离 Δs=d+sAB-sC=0.87 m 【点评】这道试题,滑板上表面由“粗糙+光滑+粗糙”三段组合,试题情境的复杂性和新颖性都较高,难度较大,区分度较好。解题过程中,学生需要灵活选择研究对象及其对应的运动过程,需要具备力学规律的分析推理能力和应用数学知识处理物理问题的能力,通过对物理动态过程的分析和研究,形成物理建模研究的物理思维和数理结合科学探究等学科核心素养。因此不论在知识维度,还是思维能力维度对学生要求都较高。 【例3】如图4所示,长L=5 m、质量M=1 kg的滑板静置在粗糙水平面上,滑板与水平面之间的动摩擦因数μ=0.1,滑板的上表面由不同材料构成。质量m=1 kg的小物块静止在滑板左端的O点,物块与滑板OA段、AB段、BC段之间的动摩擦因数分别为μ1=0.3、μ2=0.1和μ3=0.5。从t=0开始对物块施加一水平拉力F,F随时间t变化关系如图5所示,取水平向右为正方向。已知OA、AB段长度分别为L1=1.0 m、L2=3.0 m,重力加速度g=10 m/s2。求: (1)物块到达滑板上表面A点时的速度大小v1; (2)第2 s内物块与滑板之间的摩擦产生的热量Q; (3)最终物块与滑板都静止时,物块距滑板右端C的距离d。 图4 图5 另外,此题也可以应用v-t图像法进行解答,通过分析和计算,整个过程的物块、滑板v-t图像如图6所示,这种方法可以让学生领悟到每一个过程的临界状态,找出隐含条件,找出临界值,体会用v-t图像辅助解题的优越性。 图6 【点评】这道试题,滑板上表面是“不同粗糙程度”的三段组合,学生需要在识图、读题、审题过后,通过定量计算,判断得出,第1 s内,物块相对滑板向右滑动;第2 s末,物块刚好运动到达滑板上的B点处;然后物块匀减速运动,滑板匀加速运动,第2.4 s末,物块与滑板共速,然后共同减速,到第3 s末,物块与滑板恰好停止。物块和滑板经历了四个运动过程,解题过程难在力学规律的选择,难在隐含条件的挖掘,难在假设法的思维判断。 这道试题,考查学生的审题、知识迁移和综合分析推理能力,能够促进学生更好地理解物理世界,给不同水平的学生留有发挥的空间,有很好的区分度。 图7 图8 (1)物块滑离滑板时的速率v; (2)若解除滑板的锁定并撤去上表面的材料后,物块与滑板上表面间的动摩擦因数μ=0.2,物块仍从圆弧最高点A由静止释放,求物块落地时距滑板右端的水平距离。 【点评】这道试题,创设了滑板上表面“动摩擦因数均匀变化”的新情境,但降低了运动的复杂性,降低了试题的难度。需要注意的是,在对不同年级、不同层次学生的命题中要控制好试题情境的水平层级。 例4中,由于滑板上表面的动摩擦因数均匀(线性)变化,摩擦力的大小线性变化,摩擦力做功是变力做功,采用平均值法进行计算,简化了解题过程。另外,滑板并不是薄板,物块滑离滑板后做平抛运动,受力情况发生突变,滑板不是做匀加速运动,而是做匀速直线运动,解题过程中需要注意这一点,避免错解。 问题的复杂程度与情境的复杂性、内容的抽象性和应用的综合性密切相关。对“板块模型”的滑板上表面做文章,稍作变更、拓展,多角度进行设问,便可以编制出一些培养学生物理观念、科学思维的优秀试题。通过灵活运用有关物理知识和方法解答一系列相似的“板块模型”题,有利于开拓解题思路,提升物理学科核心素养。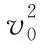
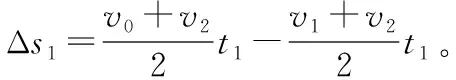
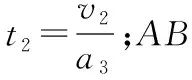
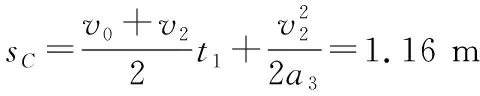
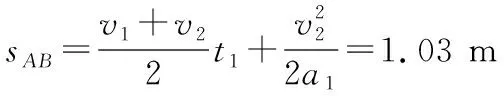
三、滑板上表面是“不同粗糙程度”的三段组合


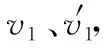

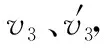
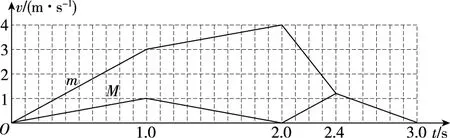
四、滑板上表面“动摩擦因数均匀变化”的情境
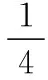
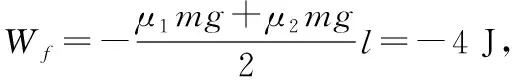
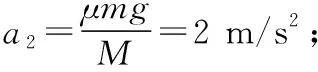
五、结束语

