恒生指数期货与国际指数之间的关联性研究
2022-01-19张宇宸河北金融学院
文/张宇宸(河北金融学院)
一、研究背景
现如今全球金融市场之间相互关联性越来越明显,中美日金融市场波动可能会影响到全球投资者的信心,从而使金融市场具有一定相关性,产生或同向或反向的影响。吴世农(2005),罗旋(2006),石建勋(2011)对A股与H股市场之间是否存在影响及影响效果进行研究。罗旋(2006)认为两地股市存在着因果关系但不存在协整关系。而吴世农(2005)认为两地股市存在协整关系。石建勋(2011)则认为在金融危机后两地股市的协整关系发生了变化。丁振辉(2013)研究发现A股对H股市场的影响更大。全球疫情减缓了全球化经济的发展,同样也会影响全球金融市场之间的关联性。同时这一影响也会对恒生指数期货与其他市场指数的影响关系发生变化。杨雪莱(2012)研究发现在危机期间中国和美国金融市场联动性增强。在全球市场化进程受阻、美联储不断实行量化宽松政策、疫情对全球贸易和经济造成巨大冲击等一系列因素的影响下,全球指数对恒生指数期货的影响如何变化有待研究。因为研究国际间指数的互相影响及作用效果,不但可以对相关投资者提供指导,同时也可以为全球经济影响提供一定借鉴价值。香港金融市场作为中国较为特殊金融市场,在经济方面受到中国大陆经济政策变化的影响,同时也会受到大陆居民生活消费的影响。这些影响的混合效果足以对香港金融市场产生不可忽视的作用。港币以美元为抵押物发行,在汇率方面受到美元汇率的影响,使得两种货币有十分强的关系。香港以港币作为计价单位,天然受到美元汇率波动的影响,其金融市场同样会受到美国金融市场的影响。加上香港市场开放的金融环境,是外国资本进入中国的入口。美国金融市场对香港金融市场有较为明显的影响。日本作为亚洲的发达国家,其贸易活动,金融市场对亚太区域金融影响较大,同样会对香港金融市场产生一定影响。本文利用收盘价数据分析恒生指数期货受到中美日三国指数影响的情况,探讨三大金融市场对中国香港金融市场的影响程度,并通过数据分析,判断是否能够通过国际指数变化来指导在恒生指数期货上的投资。
二、数据选择与处理
要研究中美日金融市场对恒生指数期货的影响,需要选取这三国具有代表性的指数进行分析。中国市场指数选择覆盖范围较大的上证指数,美国市场指数选择覆盖互联网信息技术公司较多的纳斯达克指数,日本市场指数则选择最为经典的日经225指数。数据时间段选取从2017年6月8日到2020年12月20日共三年6个月的数据,数据来源于东方财富CHOICE数据终端。
不同区域、国家的金融市场会受到地区所在时区不同,交易所规定的每天开市、闭市的时间不相同以及各国节假日的不同等一系列因素的影响,且市场间影响可能具有迟滞性,而可能会迟滞一段时间。所以选取数据时采用各指数的日数据作为研究数据,而不是以5分钟等更短周期的数据来研究恒生指数期货受到国际指数的影响。考虑到恒生指数期货是一个带杠杆的保证金交易,每日指数波动剧烈。如果国际金融市场对恒生指数期货的影响在同一天的交易中没能反映出来,考虑到在下一个交易日又会受到新的价格变化的影响,可以忽略上一交易日其他市场对恒生指数的影响,所以也不选择比日数据更长周期的数据,因为不同区域、国家金融市场因为节假日或特殊原因开市的日期也有所不同。为了真实反映国际指数与恒生指数期货的关联性,在处理数据时将几个市场同一天开市的数据保留,剔除其他数据,减少噪声数据干扰。
三、研究方法
关联性分析包含多种分析方式,本文采用相关系数方法对指数市场进行相关性分析,简单判断指数市场间的相关性。并使用回归分析来研究数据之间的关联性。再使用ADF检验,判断序列是否具有单位根,原假设是否被拒绝,从而判断相关系数是否可信,时间序列是否平稳。
待分析相关性的两个数据序列,在进行相关性分析之前,通常假设两列数据之间没有相关性,避免影响最终结果判断。在进行相关性分析之后,能够获得两个量化指标:相关系数和显著性检验概率。检验概率值反映了没有相关性的可能性。在95%的置信度下,若数值小于0.05,则否定了原假设,两个数据序列不相关。通过这一方法就可以判断两个序列数据的相关程度及可信度。相关系数的符号说明数据之间是正相关还是负相关,这一方法无法判断各因素影响的因果关系,同时本文的研究目的也不需要对因素因果关系进行研究,只需对影响的显著性及可信度进行判断。
本文通过回归分析法,将其他市场的指数数据作为自变量,香港恒生指数作为因变量进行分析。从理论上来说,每组变量在进行回归分析之后,都能产生不少于一个的回归方程。通过计算得出系数,并将计算所得数据带入回归方程后才能得出结果,还必须考察回归方程的有效性,只有有效的回归方程,才有用来指导因变量在自变量影响下变化的数值。使用有效的回归方程,人们可以将自变量数据代入方程,计算出想要知道的因变量值,从而可以实现预测、分析、指导等。在回归分析中,评价回归方程的质量非常重要,借助高质量的回归方程式,可以保证研究活动的科学性和有效性。反之,如果回归方程的质量很差,则可能做出完全错误的预测、分析、指导。
将上证指数、纳斯达克指数、日经225指数、恒生指数期货数据计算出两两相关系数,可以简单表明这些数据之间相关密切程度。以恒生指数期货作为因变量,上证指数、纳斯达克指数、日经225指数作为自变量进行回归分析,可以知道这三个指数能够解释多少恒生指数期货的变动。
ADF检验置信度设置为95%
零假设:上证指数与恒生指数期货相关系数为0
纳斯达克指数与恒生指数期货相关系数为0
日经225指数与恒生指数期货相关系数为0
如果p值大于0.05则不能拒绝零假设,如果p值小于等于0.05则可以拒绝零假设。
通过回归方程找到恒生指数期货与上证指数、纳斯达克指数、日经225指数的关系。
四、实证研究
(一)相关系数分析
表1数据表明恒生指数期货其他三个市场的指数都有一定的相关性。从图中数据可知纳斯达克指数期货与恒生指数期货的相关系数为-0.4252,为负相关;日经指数与恒生指数期货的相关系数为0.1835,为正相关;上证指数与恒生指数期货的相关系数为0.3117,为正相关。虽然上表数据可以得知其他三个市场指数对恒生指数期货具有一定影响,但系数不够大,不能判断有明显影响。
(二)回归分析
将恒生指数期货日收盘价格以Y表示,美国纳斯达克指数日收盘价以N表示,中国上证指数日收盘价以S表示,日本日经指数以J表示,构建回归方程。
其中a、b、c、d为未知系数。
使用四个市场的日收盘价进行回归分析。
表2数据中,R²数值表明在回归分析中该回归方程能够解释恒生指数期货变化的99.74%的数据,R²大于70%就表明拟合度足够高该回归方程具有指导意义,表中R²数据达到了99%说明该回归方程基本能解释在数据采集时间段的所有因变量恒生指数期货的变动。
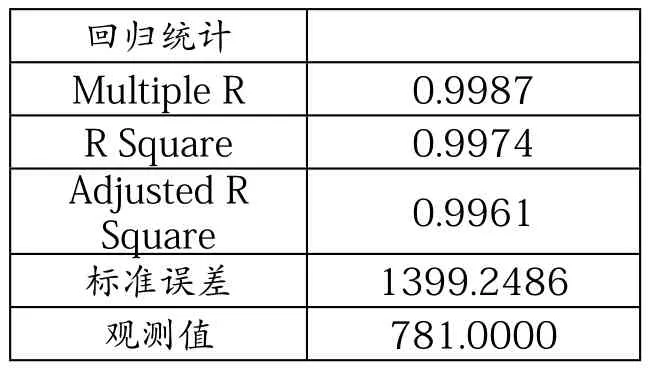
表2 回归分析结果
(三)方差分析
表3数据F值为99493.1201,Significant F为0<0.05,表明该回归方程在95%的置信度下否定原假设恒生指数期货不能由本文选取的其他三个金融市场指数解释其价格变化。这说明了恒生指数期货的价格变化完全可以由其他三个指数市场来解释。

表3 方差分析
(四)ADF检验
表4数据中纳斯达克指数的t值-35.6352明显小于-2,且p值为0<0.05,表明在95%置信度下该序列中没有单位根,即其序列是平稳的。拒绝了零假设即纳斯达克指数与恒生指数期货不相关,表明了纳斯达克指数与恒生指数期货相关。

表4 ADF检验
表4数据中日经225指数t值41.8545明显大于2,且p值为0<0.05,表明在95%置信度下该序列中没有单位根,即其序列是平稳的。拒绝了零假设即日经225指数与恒生指数期货不相关,表明了日经225指数与恒生指数期货相关。
表4数据中上证指数t值20.2677明显大于2,且p值为0<0.05,表明在95%置信度下该序列中没有单位根,即其序列是平稳的。拒绝了零假设即上证指数与恒生指数期货不相关,而表明上证指数与恒生指数期货相关。
从系数一栏可以得知各指数与恒生指数期货之间的变动关系。纳斯达克指数系数一栏为-1.4355,这一数据表明当纳斯达克指数变动1个点的时候会导致恒生指数期货产生1.4355个点的反向变动。日经225指数系数一栏为1.2761,这一数据表明日经225字数变动1个点会导致恒生指数期货产生1.2761个点的同向变动。上证指数系数一栏为3.5935,这一数据表明上证指数变动1个点会导致恒生指数期货产生3.5935个点的同向变动。
五、结论
综上,该回归方程能够解释数据占比达到了99.74%,是个非常高的水准。这可能是数据选择时间段导致的,在这段时间国际上发生了很多具有全球影响力的事件,导致全球金融市场关联性增大。尤其是香港金融市场与其他金融市场的关联性增大,导致了恒生指数期货与上证指数、纳斯达克指数、日经225指数之间的关联性增大了。得到的回归方程时间序列平稳,没有单位根。故从2017年6月8日到2020年12月20日之间的日收盘数据能够很好地拟合由上证指数、纳斯达克指数、日经225指数作为因变量,系数分别为3.5935、-1.4355、1.2761的回归方程。
按照回归分析得到的数据,可以知道美国的纳斯达克指数上涨会给目标指数期货带来下降的影响,即负相关。而日经225指数与上证指数会对目标指数期货带来相同方向变动的影响。在实际交易中利用不同金融市场的开市时间,根据开盘后日经225指数、纳斯达克指数、上证指数的表现可以作为交易恒生指数期货的指导。分析结果是由三个自变量组成,所以在实际运用时需要综合考虑三个市场的变动。如果纳斯达克指数下跌,上证指数、日经225指数上涨,该回归方程可以直接预测恒生指数期货会上涨。但如果纳斯达克指数、上证指数、日经225指数同时上涨就需要使用各指数上涨点数乘各指数相关系数求和来预测恒生指数期货到底是上涨还是下跌。
金融市场风云变幻,现在的高相关联性不代表未来一直如此。金融市场间的关系可能会随着时间发展,受到国家政策,突发性国际事件的影响产生剧烈变化。本文采用最近三年多的数据来进行分析,具有一定时效性。利用历史数据得到的回归方程只是对历史数据关系的分析,对未来的恒生指数期货交易具有一定指导意义,但未来金融市场还有很大的不确定性,不能完全依赖这个回归方程。尤其是近一年全球疫情对于全球经济、金融市场的影响很大,而这段时间的数据在本文选取的数据中占有较大比重。对于未来全球市场可能的变化需要不断纳入新的数据,调整回归方程的系数来应对金融市场关联性的变化。甚至当全球金融市场发生剧烈变化时,回归分析中部分指数的p值可能会大于0.05,不能拒绝零假设。即不能否定该指数与恒生指数期货的相关系数为0,这时该指数对于恒生指数期货的交易没有任何指导作用。
