基于磁链函数的BLDCM无位置传感器控制方法研究

武紫玉， 黄元峰， 王海峰， 李 旺

（1.北京交通大学电子信息工程学院，北京 100044；2.交控科技股份有限公司，北京 100070；3.中国科学院电工研究所，北京 100190；4.北京云道智研科技有限公司，北京 100192）

0 引言

由于功率密度高、控制简单，永磁无刷直流电机（Brushless DC Motor，BLDCM）在民用、航天以及军事等方面得到了广泛应用。BLDCM需要位置传感器指导电力电子开关换相，但位置传感器的存在不利于BLDCM的使用。安装传感器会增加工艺复杂程度以及电机的质量和体积，若安装不当，会使电机产生较大的转矩／电流脉动。因此，针对BLDCM无位置传感器控制的研究越来越多。

BLDCM无位置传感器控制方法主要包括[1-2]：反电势过零点检测方法、状态观测器法、高频注入法、电流波动法等。其中，反电势过零点检测方法的研究和应用最为广泛。文献[3]通过分析关断相反电势为0时的端电压值，检测关断相的端电压在PWM导通或关断时候的值，并与反电势为0时对应的端电压值对比，以此判断换相。由于该方法存在低速时反电势信号较弱无法辨识出换相信号的问题，并且由于相反电势过零点超前换相点30°，需对检测到的过零信号进行相移才能得到换相信号。文献[4]、文献[5]采用线反电势过零点判断电机换相，解决了相移的问题。文献[6]对三相端电压求和后积分得到三次谐波反电势，通过比较其过零点得到换相信号。电压的检测、求和、积分和换相点判断均通过模拟电路实现，响应速度快，因而无位置传感器控制的转速可以达到上万转。不过，这种控制方法低速时积分器误差较大，性能很差。二极管续流检测法是基于关断相反电势过零时二极管导通的原理，文献[7]采用该方法控制电机换相，由于不受反电势幅值限制，该方法将无位置传感器算法的转速适用范围进行了拓展，但该方法需要六路独立供电的硬件检测电路，硬件较为复杂，因而应用不多。观测器法是近年来研究较多的一种方法，文献[8]采用了滑模观测器法，该方法能够对定子电阻进行估算，实现了电机低速带载启动。

电机在低速时反电势信号弱，难以检测。高速时换相频率高，因而给无位置传感器控制带了挑战，许多学者针对该问题进行了研究。文献[9]采用三电压矢量作用下的电流响应来判断电机低速时的位置。文献[10]、文献[11]提出了一种磁链函数法，该方法将电机两相反电势作商得到磁链函数。由于磁链函数与转速解耦，低速时对换相位置的辨识能力较强，因而该方法得多了越来越多的关注。文献[10]、文献[12]和文献[13]在磁链函数方法基础上对位置误差进行补偿，从而实现了全速度范围内的控制。然而，磁链函数法阈值设置不当会导致在高速时换相点的丢失。针对此，本文提出了一种改进的磁链函数方法，该方法保留了磁链函数与转速解耦的特性，同时也解决了高速区换相点丢失的问题。

1 改进磁链函数法换相原理

1.1 BLDCM数学模型

永磁无刷直流电机及驱动系统等效电路如图1所示，直流母线经过三相六桥臂IGBT开关管后与电机绕组相连。在120°导通方式中，任一时刻电机仅两相绕组通电，电机正转时绕组按照如下顺序依次通电： A+B-、 A+C-、 B+C-、 B+A-、 C+A-、 C+B-。

图1 BLDCM及驱动系统等效电路图Fig.1 Equivalent circuit diagram of BLDCM and drive system

忽略定子谐波在转子中感应的电流，忽略杂散损耗和铁耗，假设电机三相绕组对称，那么，无刷直流电机的电压方程可以描述为

式（1）中，Ua、 Ub、 Uc为电机的三相相电压，ia、ib、ic为电机的三相绕组电流，ea、eb、ec为电机的三相绕组反电势，R为绕组电阻，LS为电机相电感，LM为相间互感。BLDCM三相绕组反电势及对应电流的波形如图2所示。

图2 BLDCM反电势与电流波形图Fig.2 Waveform of BLDCM back-EMF and current

由图2可知，相反电势过零点超前换相点（S1～S6）30°，而线反电势过零点与换相点重合，无需进行相移，故本文选取电机线反电势进行换相研究。

1.2 改进磁链函数法换相原理

BLDCM线电压方程如下

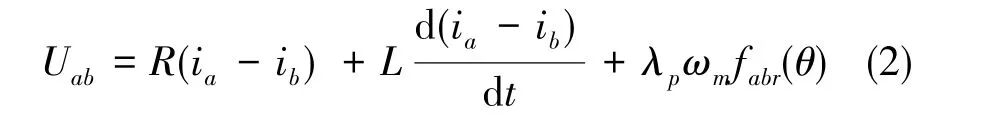
式（2）中， λp为磁链， ωm为转速， fabr（θ）是一个与转子位置相关的函数，范围为-1～1。由式（2）可知，线反电势中包含有转子位置信息以及转速信息。当电机转速较小时，反电势的幅值也较小，难以检测。为了剔除转速的影响，在判断换相点时将两个线反电势作商，仅仅留下转子位置的影响，即得到磁链函数。

以A、B相导通换相到A、C相导通为例，由图2可知，最佳换相点在S2点。以S2为例，传统的磁链函数G1定义如下

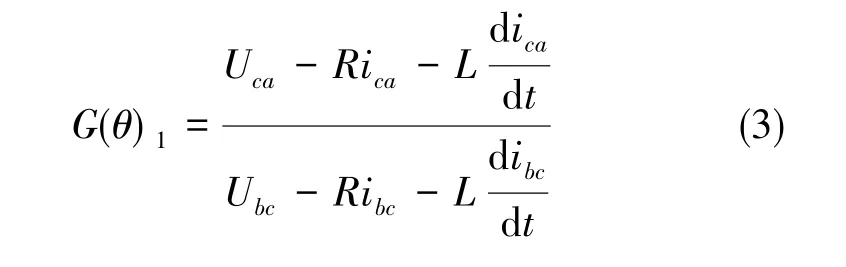
在S1～S2期间， 反电势 eca从0逐渐下降到-Ep（Ep为反电势峰值），反电势ebc由 -Ep逐渐增大到0，两个反电势作商，那么磁链函数在S1～S2将由0逐渐上升到最大值。当计算的G1大于阈值threH时，控制电机换相，该方法为传统的磁链函数换相方法。但是，该方法存在以下缺陷：在系统采样频率固定的情况下，随着电机转速的提升，反电势周期越来越短，在一个电周期采集到的反电势点数越来越少，造成在换相点附近采集到的反电势信号偏离过零点越来越多，相应计算得到的G值也会越来越小。当转速逐渐升高使得在换相点处的G值下降到小于阈值threH时，在理想换相点处算法将无法辨识出换相信号。错过换相点后，G函数波形会迅速下降变为负值，更加不会出现超过阈值threH的现象，从而造成换相信号丢失，产生电机堵转的严重问题。

为了解决磁链函数法在高速时换相失败的问题，本文提出了一种新的改进换相函数的方法。改进换相函数F（θ）将磁链函数G1整体向后平移60°电角度，将换相判据改为f＞0。 改进换相函数F（θ）3和A相电流的对应波形如图3所示。由图3可知，在换相函数 F（θ）3对应的电机换相点（Q1～Q5）处， 改进换相函数由负到正穿过零点，若电机在理想换相点前一个采样点处未检测到f＞0，那么在理想换相点后的第一个采样点处计算的换相函数F的值必然大于阈值0，控制算法仍然能辨识出换相信号。

图3 改进换相函数以及A相电流波形Fig.3 Waveform of improved commutation function and current A

当电机转子轴处在不同的位置区间时，按照表1计算相应的改进换相函数。当计算得到的改进换相函数F由负值转变为正值时，说明电机转子运行到对应的换相点，触发开关管换相，即可实现BLDCM的无位置传感器运行。

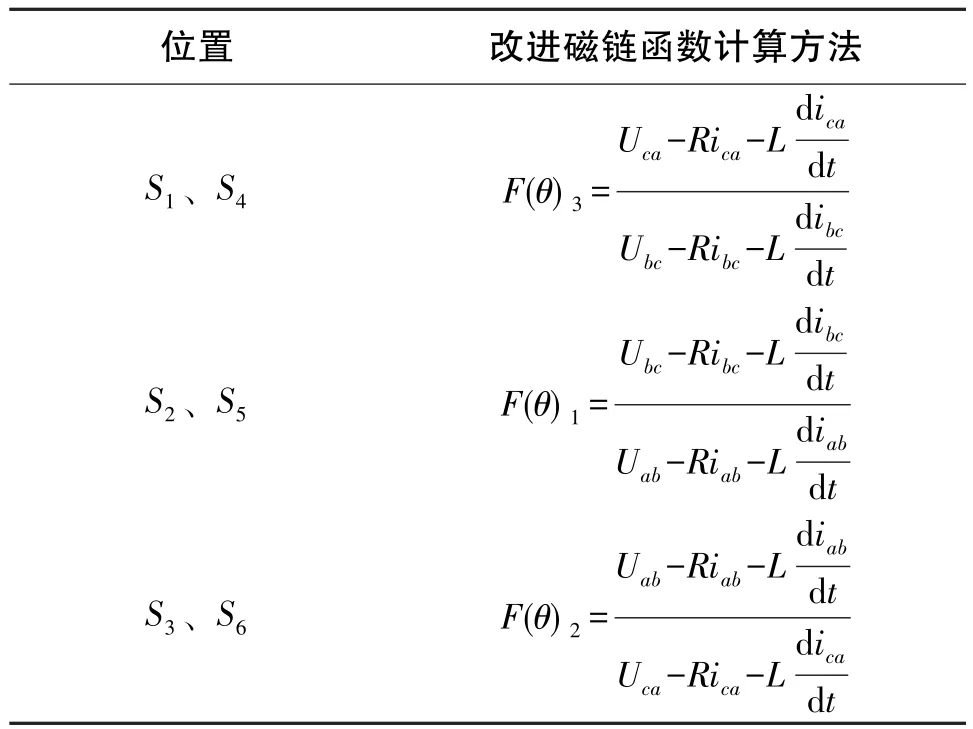
表1 不同转子位置对应的改进换相函数FTable 1 Improved commutation function at the different rotor positions

2 换相误差补偿

由表1可知，计算换相函数F需采集电机端的电压、电流、电阻以及电感参数，计算复杂。因此，本文在计算换相函数时进行了简化。在计算换相函数时首先忽略电阻电感压降，将换相函数简化为

忽略绕组电阻电感压降会带来一定的换相误差，将该误差记为θ1和θ2。由式（4）可知，为计算磁链函数需要测量电机线电压。在测量电机线电压时，滤波电路会造成相位滞后，将滤波电路造成的相位误差记为θ3。通过计算误差角度θ1、θ2和θ3并进行误差补偿，即可得到准确的换相点位置。

2.1 忽略电阻电感压降带来的相位误差

（1）忽略电阻压降

在简化计算改进换相函数F时，忽略了电阻压降，并将电阻压降带来的换相滞后角度记为θ1。 对θ1进行分析， 如图4（a）所示。 以反电势正半周期为例，若仅仅忽略电阻压降，那么计算的反电势将在t1时刻过零。因此，误差角θ1可以表示为

图4 换相误差与转速关系曲线Fig.4 Fitting curve for commutation error to speed

式（5）中，ke为反电势常数；ϕ为磁通，若不考虑饱和为常数；n为转速。由式（5）可知，换相误差角θ1与转速成反比，与电流呈正比，负号代表误差角度为超前换相。

（2）忽略电感压降θ2

考虑仅忽略电感压降，那么换相误差角度记为θ2。根据文献[14]对BLDCM换相时刻电流变化的讨论可知，考虑绕组电阻和电感时，换相期间的电机等效电路及电流波形如图5所示。

图5 BLDCM一次换相暂态分析Fig.5 Transient analysis of BLDCM one-phase commutation

假设tc为理想换相点，多数情况下tc在t1～t2之间，即前一次换相造成的续流已经结束，在该区间内电流变化缓慢，电感压降为零，那么θ2也为0。极少情况下，若电机运行的电感和电枢电流非常大，电感续流严重，tc在0～t1之间，即下一次换相来临时上一次续流仍未结束，那么需要对C相电流暂态值进行求解，进而得到电感压降。通过求解微分方程可得

可见，若电机容量较小、电感较小时，θ2近似为0。若电机电感续流严重时，忽略电感会造成换相超前，可以按照式（7）对θ2进行补偿。

2.2 电压滤波带来的相位误差

BLDCM采用PWM进行调速，端电压中包含大量开关噪声。因此，在测量电机线电压时，需要添加滤波电路。滤波电路设计需要根据电机额定工作参数进行测试，实验电机的参数如表2所示。

表2 实验电机参数Table 2 Parameters of the tested motor

由表2可知，电机额定运行时的基波频率为133Hz，PWM载波频率为 10kHz。利用 Filter Solution软件设计三阶ChebyshevⅠ型低通滤波器，设置滤波器截止频率为238Hz，选择滤波器电路结构为sallen-key结构，设计的滤波器电路如图6所示。

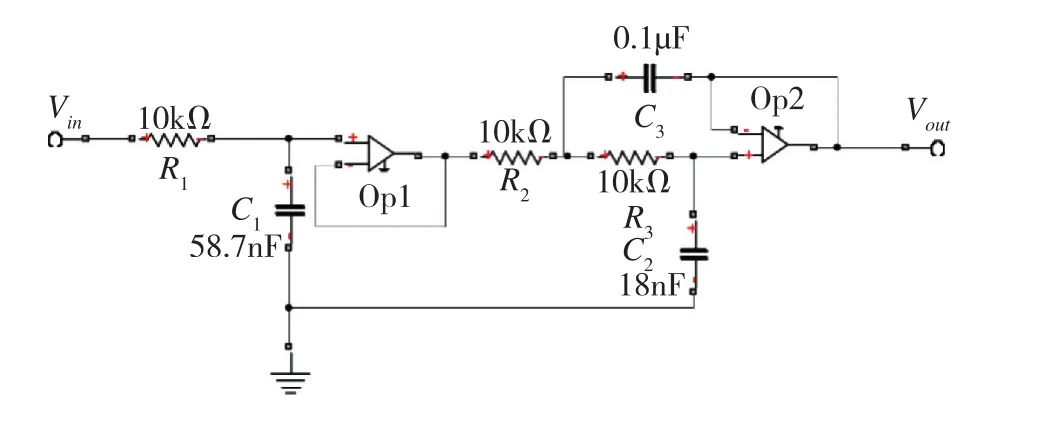
图6 三阶低通滤波器电路原理图Fig.6 Schematic diagram of third-order low-pass filter circuit

低通滤波器的存在会使测量到的电压信号产生相位滞后，将低通滤波器带来的换相误差角度记为θ3。 图6的三阶低通滤波电路由1个一阶RC低通滤波器和1个二阶RC电路串联组成，通过分析低通滤波器的传递函数，可以得到三阶低通滤波器引起的电压信号相位滞后角度

由式（8）可知，滤波器引起的测量信号滞后角度与电机转速成反正切关系，随着电机转速的提升，滞后角度逐渐增大。若按照式（8）求解补偿角度，则需要在线查询三角函数反正切表，增大了数字信号处理器的运算量，减小了控制系统的响应速度。对滞后角度θ3和转速ω的关系进行多项式拟合， 采用一次多项式对θ3和ω进行拟合，得到的拟合公式如式（9）所示，拟合误差曲线如图7所示。

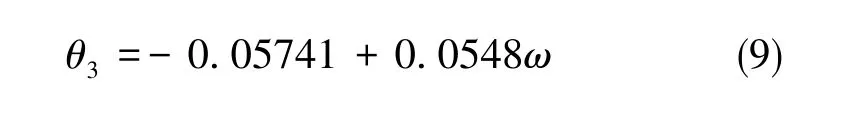
图7 一阶拟合误差曲线Fig.7 Curve of first-order fitting error

由图7可知，采用一次拟合的最大误差角为1.03°，满足误差补偿要求。

综上，总换相误差角为

通过分析换相误差来源可知，θ3与转速的关系可以用线性拟合进行表示；θ1、θ2与转速近似成反比，与绕组电流成正比。对于小功率的BLDCM，由于额定电流值较小，电阻和电感压降带来的换相误差角度θ1和θ2也很小，在相位补偿时可以只考虑滤波电路的角度延时。对于大功率的BLDCM，则需要按照式（10）计算位置补偿角度。确定换相误差角度后，按照文献[15]提出的基于坐标变换的方法对换相误差进行补偿。

3 实验

3.1 实验参数

采用表2所示的电机参数进行实验，采用本文提出的磁链函数方法控制BLDCM进行空载和带载实验，记录磁链函数和电流波形，并与位置传感器的测量信号进行对比。

3.2 低速实验

为测试本文提出的换相方法在低速时的运行性能，控制电机按开环三段式起动加速至124r／min时稳定运行，记录开环运行时的磁链函数、A相绕组电流、Hall位置传感器电压波形。在相同转速下，电机切换为本文提出的磁链函数法闭环换相控制，记录闭环运行时的波形，实验结果如图8所示。图8中，f为磁链函数值，Ia为A相绕组电流，Hall为与A相对应的Hall位置传感器电压信号。 对比图8（a）和图8（b）可知， 切换为本文提出的换相方法后，电机换相误差时间大大缩短。同时，由于降低了电机换相误差，相比开环的控制方法，电机的空载电流也明显下降。

图8 低速时的磁链函数、A相绕组电流、Hall位置信号波形对比Fig.8 Waveform comparison among flux linkage function，winding current A and Hall position signal at low speed

为测试无位置传感器算法的起动性能，分别测试了闭环控制下的空载起动和带载起动过程，实验结果如图9所示。由图9（a）可知，与传统三段式起动方法相比，由于闭环起动方法能够自适应地修正导通时间，从而使得给定的电压换相频率能够跟随电流变化而改变，电机转速迅速上升到满足切换要求，起动时间大大缩短。同时，最大起动电流为1A，起动电流较小。不过，由于空载起动电流较小，电流值测量误差较大，闭环控制算法在绕组电流第一个正向导通区间存在误判的现象，过早地切换，起动转矩过小，无法使电机克服负载起动转矩。当A相绕组第二次正向导通时，电机才产生足够的电磁转矩起动，控制算法因而识别出换相点，使得电机完成加速和起动。由图9（b）可知，当电机带1.22N·m负载起动时，闭环控制算法换相误差较小，始终低于60°，电机能够产生持续较大的电磁转矩，使得电机能够带较大负载迅速起动。

图9 低转速闭环控制下的电流及换相位置波形对比Fig.9 Waveform comparison between current and commutation position under low speed closed-loop control

3.3 中高速实验

对电机进行转速、电流双闭环PI控制，转速给定600r／min，电机分别加载1N·m和3N·m负载。利用本文提出的磁链函数方法控制电机换相，并利用式（10）对换相误差角度进行补偿，记录不同负载下辨识的改进换相函数值f、Hall位置信号以及A相绕组电流波形，实验结果如图10所示。

图10 带载电流及换相位置波形对比Fig.10 Waveform comparison between current and commutation position with load

由图10可知，负载变化时，无位置传感器算法辨识的换相点与Hall位置传感器测量的换相点一致，电流波形理想，电机运行良好，这说明本文提出的误差补偿算法可行。有带载的情况下，无位置传感器算法仍能够准确地辨识出BLDCM的换相位置，换相误差很小。

逐步提高电机转速给定值，电机在本文提出的无位置传感器控制算法下换相，测试电机额定转速范围内无位置传感器控制方法的有效性及效果。利用示波器采集电机不同运行转速时A相绕组电流波形以及对应的Hall位置信号波形，实验结果如图11所示。

图11 中高速下绕组电流及换相位置波形对比Fig.11 Waveform comparison between current and commutation position at medium and high speed

由图11可知，在电机中高速运行阶段，本文提出的换相函数F辨识的换相点与Hall位置传感器得到的换相点基本重合，BLDCM在无位置传感器控制下的换相误差很小，空载电流小，换相控制效果好。

在相同硬件条件和采样频率下，采用式（3）中的原始磁链函数方法控制电机换相，阈值设为20。实验发现，当电机转速提升至1200r／min时，出现了换相点丢失、电机过流报警的问题。可见，在相同采样和控制频率下，改进的磁链函数方法能够辨识出更高转速下的换相信号。

4 结论

本文提出了一种新的改进磁链函数方法的BLDCM无位置传感器控制方法，该方法具有以下优点：1）改进磁链函数方法与转速解耦，低速时仍能很好地辨识出换相信号；2）在相同采样和控制频率下，能够辨识出更高转速下的换相信号，拓展了无位置传感器控制算法的转速适用范围；3）对电阻电感压降以及滤波电路带来的换相误差角度进行了分析，推导了换相误差角度与转速和电流的关系，并通过实验验证了换相控制算法的准确性。

受实验条件限制，本文并未对电机高速下的带载情况进行测试，带载实验未覆盖电机全转速范围。本文虽然讨论了续流严重时绕组电感带来的换相误差角度，但是由于实验时电机输出功率较小，并未考虑电感压降带来的误差。值得注意的是，随着负载增大，电机绕组电流增大，由电感续流引起的换相误差对电机性能的影响越来越大，因此有必要对该部分内容进行进一步测试和优化，从而使基于改进磁链函数方法的无位置传感器控制能够更广泛地应用到BLDCM上。