基于深度学习的知识追踪研究进展

刘铁园 陈 威 常 亮 古天龙,3

1(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)2(桂林电子科技大学电子工程与自动化学院 广西桂林 541004)3(暨南大学信息科学与技术学院/网络安全学院 广州 510632)

近年来，随着智能辅导系统(intelligent tutoring system, ITS)和大型开放式网络课程(massive open online courses, MOOCs)等在线教育平台的发展和普及，数百万的用户选择通过在线平台学习.相比传统的线下教育，在线学习系统最显著的优势在于其能保留学习者详尽的学习轨迹，提供了调查不同轨迹下学习者行为效能的条件[1].然而，在线学习平台上学生与教师人数的悬殊使人工的辅导变得不现实.如何利用在线学习系统的优势，从学生的学习轨迹中挖掘出潜在的学习规律，以提供个性化的指导，达到人工智能辅助教育的目的，成为了研究者密切关注的问题.

知识追踪(knowledge tracing, KT)是实现人工智能辅助教育的有力工具，目前已经成为了ITS的一个主要组成部分[2]，被广泛应用于各个在线教育平台，如edX[3]、Coursera[4]和爱学习[5].KT旨在建立学生知识状态随时间变化的模型，以判断学生对知识的掌握程度.通常情况下，KT的任务可以被形式化为一个有监督的序列学习任务，给出学生的历史学习交互记录It={i1,i2,…,it}，通过预设的模型从中提取出学生隐式的知识状态，并追踪其随时间的变化.学习交互通常表示为一个题目-答案元组it=(qt,at)，意为学生在时刻t回答了问题qt，at则指示了回答的情况.由于很难直接衡量学习者的实际学习状态，现有的KT模型通常采用一种替代解决方案，使模型预测下一个题目答对的概率P(at+1=correct|qt+1,It).

BKT(Bayesian knowledge tracing)模型[6]是目前最流行的KT模型之一，BKT将学习者的潜在知识状态建模为一组二元变量，代表是否掌握某个知识成分(knowledge component, KC).KC可以被泛化地理解为知识概念、原理、事实或者技能.对于一个具体的题目qt，KC可以视作答对qt所必须掌握的知识.在单KC模型中(即一个题目对应一个KC)，题目与KC可以视为是等价的.

在每一次学习交互后，BKT使用隐Markov模型(hidden Markov model, HMM)更新这些二元变量的概率.在提出后的20年来，BKT一直被视为KT领域的首选方法，其他机器学习模型，如BKT的变体[7]、逻辑回归的变体[8]以及项目反应理论[9](item response theory, IRT)与BKT的性能差异都很小[10].

虽然BKT在KT领域取得了很大成功，但是其本身也存在着很大的问题.首先，变量与KC之间的对应是模糊的，无法做到一一对应，且二元变量的设置不符合现实中的学习过程[11].其次，对每个KC分开建模的方式使BKT无法捕捉不同KC间的关系，也丧失了对未定义KC和复杂KC的建模能力.

深度学习以其强大的特征提取能力引起了研究者的广泛关注，许多研究者将其应用到KT领域，称为基于深度学习的知识追踪(deep learning based knowledge tracing, DLKT).相对于传统的机器学习模型，DLKT不需要人工标注的KC信息，且能够捕捉到更复杂的学生知识表征，还可以发现并利用KC之间的关联信息.目前，对DLKT的研究已经成为了KT领域的一大研究热点.

DLKT的开创性工作深度知识追踪(deep knowledge tracing, DKT)模型[11]于2015年提出，在2015年后，涉及到KT领域的代表性综述性论文有文献[1，12-16].其中，文献[1]从知识点、学习者和数据3方面总结了KT模型在教育领域的应用.文献[12]侧重于讨论特定场景下模型的选择问题.文献[13]将学习者模型分为知识状态、认知行为、情感、综合4类并做了详细阐述，KT模型属于其中的知识状态模型.文献[14-16]对目前的KT模型从教育角色、教育过程等角度进行了梳理和分析比较，但侧重在机器学习，且其中所涉及的模型较少，仅介绍了几个具有代表性的模型.总体来说，这些文献涉及到DLKT模型的内容较少，没有聚焦于DLKT领域.

本文着眼于DLKT领域的相关研究，对该领域的技术演化和最新研究进展进行了系统性的调研与梳理.

1 基于深度学习的知识追踪DLKT

1.1 DLKT相关研究概览

我们查阅了近5年半(2015-01—2020-06)DLKT的相关论文.其中，中文文献来源于中国知网(CNKI)，英文文献来自IEEE Electronic Library，Elsevier Science，EI Compendex，Web of Science，Springer Link，ACM Digital Library等数据库，并使用学术搜索引擎(谷歌学术、百度学术、必应学术)查漏补缺.在检索时，中文使用“知识追踪”和“深度知识追踪”作为关键词，英文使用“knowledge tracing”和“deep knowledge tracing”为关键词.对获得的相关文献进行分析整理，去掉不相关的和没有使用深度学习方法的文献，共筛选出69篇文献，图1给出了这些文献的发表情况.

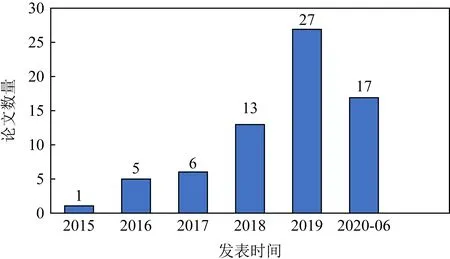
Fig. 1 Publication of DLKT related literatures in recent five and a half years

可以看出，近5年半DLKT相关文献在国内外发文量呈明显上升趋势，在新冠疫情导致许多会议延期的前提下，2020年上半年也有17篇论文发表.

发表仅5年，DLKT的开创性工作DKT就有433次引用(数据来源：谷歌学术)，相关研究在NIPS，AAAI,SIGIR,WWW等顶会上均有报道，可见该领域研究被学界的认可和接受.

1.2 符号定义

在本节，我们给出文中常见符号的定义(其他非常见符号以文中说明为准)，表1展示了每种符号的代表含义.除特殊说明外，本文使用的符号皆以表1为准.我们使用kt表示知识成分KC，qt代表题目，at代表对应的回答，下标t指示了时刻(如无必要，则省略).两者的组合(qt,at)构成了一个学习交互xt.通常情况下，KC与题目存在对应关系，两者可以相互转化，因此，学习交互同样可以表示为(kt,at)，根据具体的模型选择.在时刻t，模型的预测值yt表示下一时刻回答正确的概率.使用L表示损失函数，LBCE特指二元交叉熵(binary cross entropy, BCE)函数.使用大写的粗体字母(如W)表示矩阵，使用小写的粗体字母(如b)表示向量.特别地，W和b特指权重矩阵和偏置向量.

Table 1 Symbol Definition

1.3 DLKT基本模型

Piech等人[11]提出的DKT模型是DLKT领域的开创性工作，也是DLKT领域的基本模型.DKT的结构如图2所示，其以循环神经网络(recurrent neural network, RNN)为基础结构.RNN是一种具有记忆性的序列模型，序列结构使其符合学习中的近因效应并保留了学习轨迹信息[17].这种特性使RNN(包括长短期记忆网络[18](long short term memory, LSTM)和门控循环网络[19](gated recurrent unit, GRU)等变体成为了DLKT领域使用最广泛的模型.DKT以学生的学习交互记录{i1,i2,…,it}为输入，通过one-hot编码或压缩感知[20](compress sensing)，it被转化为向量输入模型.在DKT中，RNN的隐藏状态ht被解释为学生的知识状态，ht被进一步通过一个Sigmoid激活的线性层得到预测结果yt.yt的长度等于题目数量，其每个元素代表学生正确回答对应问题的预测概率.具体的计算过程为

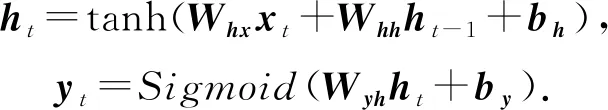
(1)

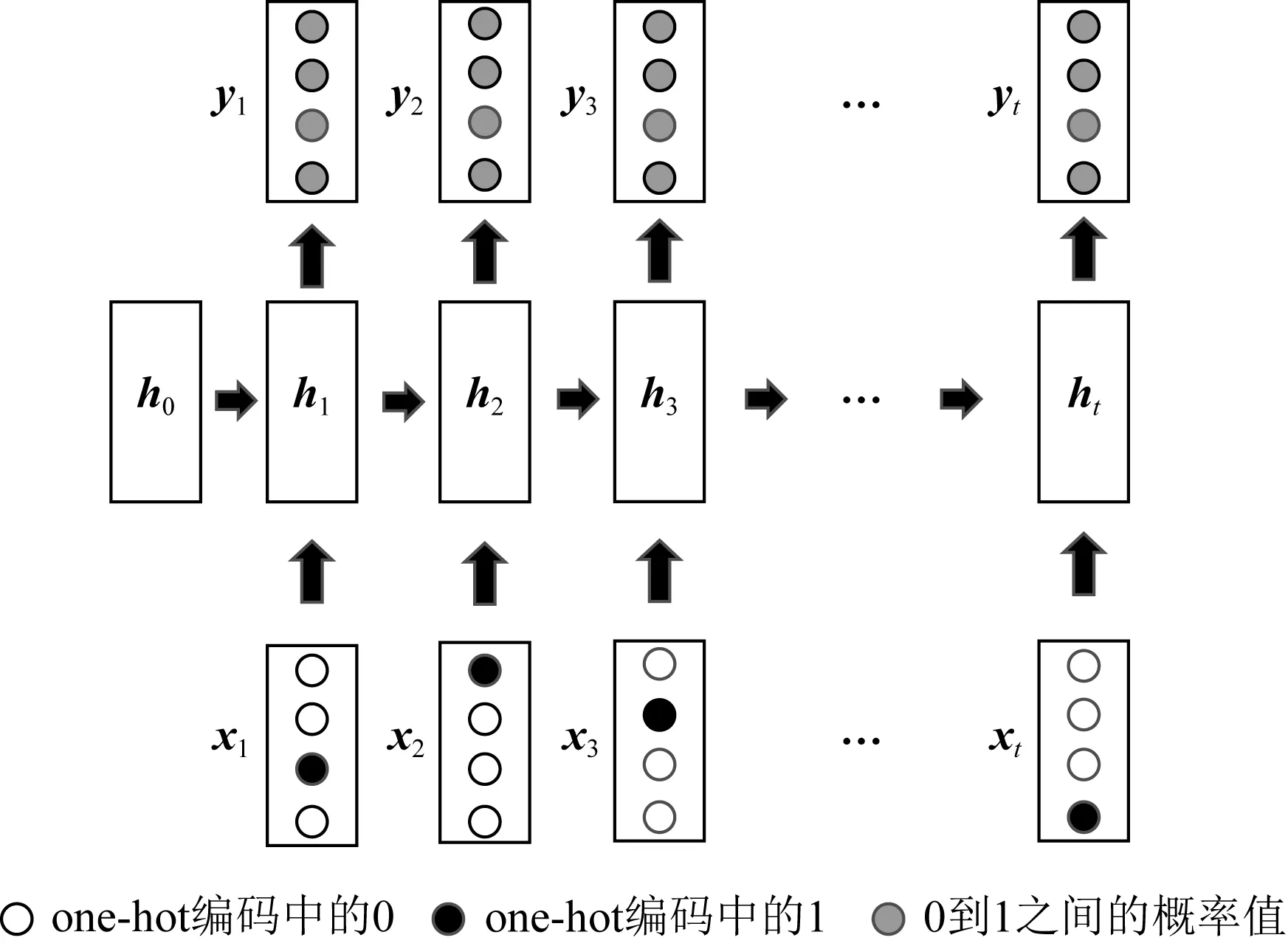
Fig. 2 Architecture for DKT model

DKT的目标函数是观测序列的非负对数似然函数，用LBCE表示二元交叉熵(BCE),则学生的损失值为

(2)

相对于以BKT为代表的传统机器学习模型，DKT不需要人工标注的数据就有更好的表现(AUC提高了20%[21])，且能够捕捉并利用更深层次的学生知识表征[22-23]，这使其非常适合以学习为中心的教学评估系统[24].

2 DKT的改进方法

尽管DKT的预测性能优于现有的经典方法，但由于它在教育应用中的实用性还有待提高，而被其他少量学者所批判[25-29].这主要是因为隐藏状态ht在本质上很难被解释为知识状态，而且DKT模型没有对知识交互进行深入分析[30]，导致其可解释性很差.

RNN存在长期依赖问题，其变体(如LSTM和GRU)仅仅提高了序列学习的容量(对于LSTM来说，容量在200左右[31])，但并没有解决问题.DKT中以RNN为基础，因此其同样存在长期依赖问题.长期依赖问题使DKT无法利用长序列的输入[32]，且会导致重构错误和波动准则[33-35].

在DKT中，模型的输入为one-hot编码的学生交互序列，而仅用交互序列作为输入浪费了在线平台所保留的丰富学习轨迹信息，且输入的学习特征太少也会影响模型的表现.

可解释性差、长期依赖问题和学习特征少是DKT模型最显著的3个问题，许多研究者致力于对其进行扩展和改进，以解决这些问题.我们将各种改进方法梳理为图3所示：

Fig. 3 DKT improved method venation diagram

2.1 针对可解释性问题的改进

根据使用方法的不同，针对可解释性问题的改进可以进一步细分为Ante-hoc可解释性方法和Post-hoc可解释性[36]方法.

2.1.1 Ante-hoc可解释性方法

Ante-hoc可解释性指模型本身内置可解释性.对于复杂的模型，可以通过构建将可解释性直接结合到具体的模型结构中的学习模型来实现模型的内置可解释性，在深度学习中，一种有效的可解释性模块就是注意力机制.此外，Ante-hoc可解释性还可以通过采用结构简单、易于理解的自解释模型实现[36].

1) 引入注意力机制

① A-DKT(attention-DKT)

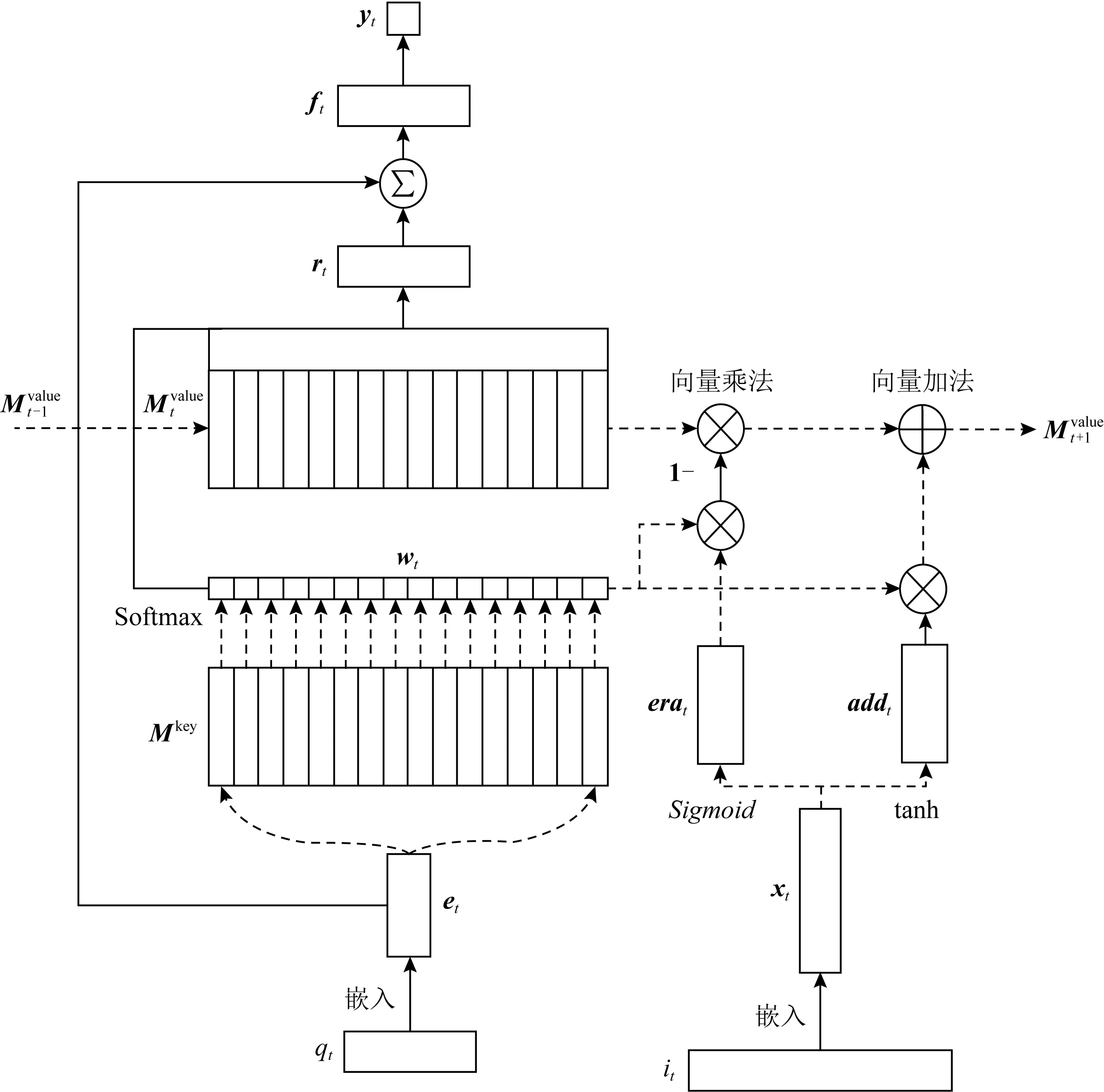
Fig. 4 Architecture for DKVMN model

Liu等人[37]在模型A-DKT中使用了Jaccard系数计算KC之间的注意力权重.设ka,kb为不同的KC，两者间的权重值为

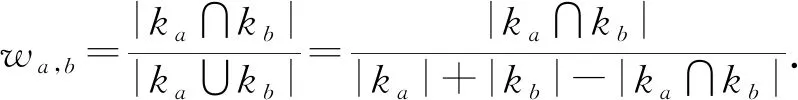
(3)

在时刻t，计算当前KC与之前所有KC的注意力权重，然后相加，得到总的注意力值wt：

(4)

最后，结合LSTM与注意力值得到预测结果：

yt=Sigmoid(Wyhht+by+wt).

(5)

② DKVMN(dynamic key-value memory network)

Zhang等人[38]受到MANN(memory-augmented neural network)的启发，提出了DKVMN模型.DKVMN使用矩阵Mkey存储KC，Mkey的每一列代表一个KC；使用矩阵Mvalue存储知识状态，Mvalue的每一列表示Mkey中对应KC的掌握程度.DKVMN的结构如所图4所示.

注意力机制主要体现在wt的计算上：在时刻t，将题目的嵌入向量et与每一个KC(即Mkey的每一列)作内积，经过一个激活函数后得到wt.wt(i)代表题目qt与KCki之间的相关性，即注意力权重：

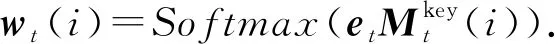
(6)

根据注意力权重计算学生对题目qt的掌握程度rt：

(7)

题目的嵌入向量et隐式地包含了难度信息，将其与rt连接，得到的ft同时包含难度和掌握程度信息：

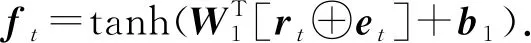
(8)

最后，ft通过一个Sigmoid激活的线性层得到学生表现的预测值yt:

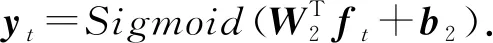
(9)

③ DKVMN-CA(concept-aware DKVMN)

Ai等人[39]进一步扩展了DKVMN模型，使其支持了人工标注的KC信息.即Mkey中的KC由人工定义，而不是机器生成.

④ EERNN(exercise-enhanced RNN)

Su等人[40]在其模型EERNN中使用了余弦相似度计算隐藏状态之间的注意力权重wt：

(10)

需要注意的是，余弦相似度计算的并不是隐藏状态之间的相似性，而是题目之间的相似性.EERNN的预测过程为：

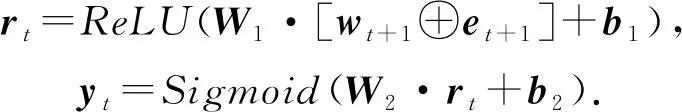
(11)

⑤ EKT(exercise-aware KT)

Huang等人[41]提出的EKT模型综合了EERNN模型与DKVMN模型，因此拥有双重注意力模块.其主要计算过程与EERNN和DKVMN模型相同，此处不再赘述.

2) 自解释模型

① KQN(knowledge query network)

Lee等人[42]用向量点积来模拟知识状态与KC的相互作用，提出了KQN模型.假设知识状态与KC都为2维向量，如图5所示，在知识状态由v2转变到v3的过程中，学生对KCk1的掌握程度由v2·k1=1增长到了v3·k1=2.这种向量化的表示与运算使KQN具有直观性和可解释性.

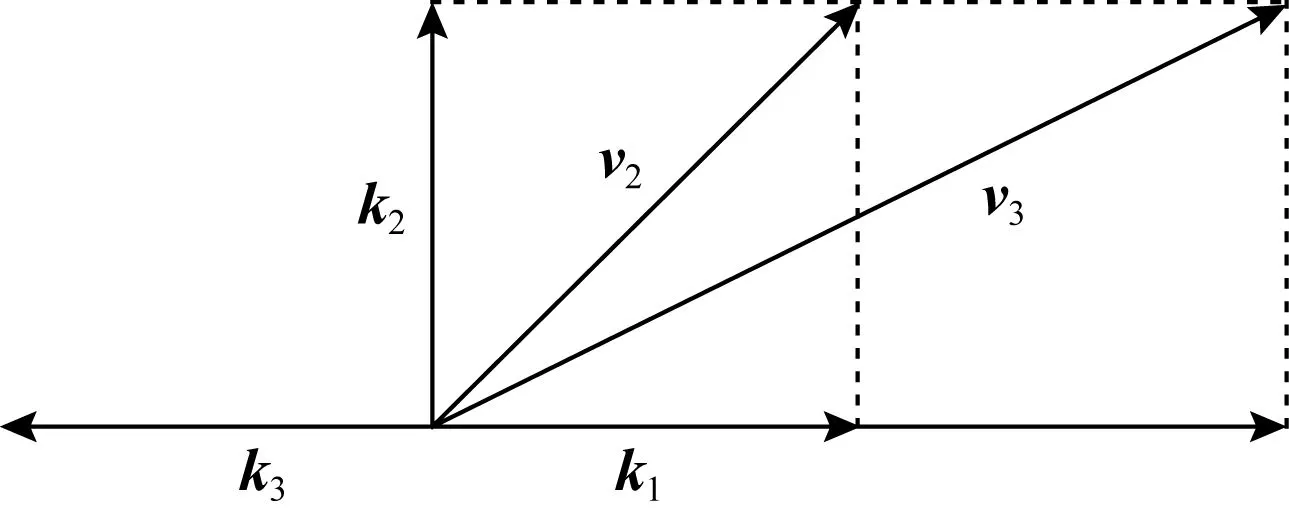
Fig. 5 An example of KQN

在KQN中，学生知识状态向量vt由RNN的隐藏状态ht经过一个全连接层得到：

vt=Wvh·ht+bv.

(12)

在时刻t，one-hot编码的KCkt+1通过一个多层感知机和L2正则化.生成新的嵌入表示：

ot+1=ReLU(W1·ReLU(W0·kt+1+b0)+b1),kt+1=L2-normalize(ot+1).

(13)

KQN用vt与vt+1的内积定义知识交互，并作出预测：

yt=Sigmoid(vt·kt+1).

(14)

② Deep-IRT(deep item response theory)

Yeung等人[43]综合了IRT理论[9]与DKVMN模型，提出了Deep-IRT模型.Deep-IRT通过2个全连接神经网络，利用DKVMN中的ft与et(式(8))分别对学生n的能力θt,n和题目难度βt建模：

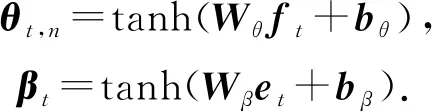
(15)

最后，通过IRT函数得出预测结果：

yt=Sigmoid(θt,n-βt).

(16)

2.1.2 Post-hoc可解释性方法

Post-hoc可解释性也称事后可解释性，发生在模型训练之后，旨在利用解释方法或构建解释模型，解释学习模型的工作机制、决策行为和决策依据[36].在DLKT领域，主要有LRP和不确定性评估方法.

1) LRP(layer-wise relevance propagation)

Lu等人[44]应用分层相关性传播方法，通过将相关性从模型的输出层反向传播到输入层，来解释基于RNN的DLKT模型.LRP的核心是利用反向传播将高层的相关性分值递归地传播到低层直至传播到输入层.具体来说，将RNN不同单元之间的连接分为加权连接和乘法连接并分别定义两者相关性的传播.如图6所示，通过计算2种类型连接的反向传播相关性，就可以对基于RNN的DLKT模型进行解释.

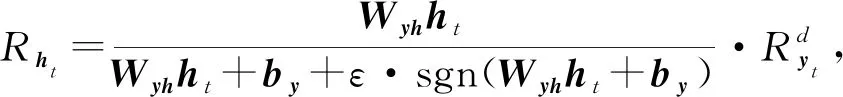
(17)

RCt=Rht,

(18)

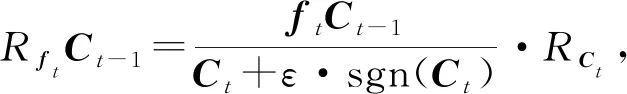
(19)

RCt-1=RftCt-1,

(20)

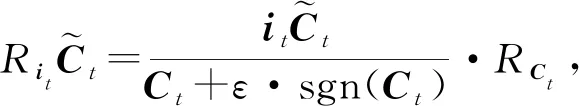
(21)

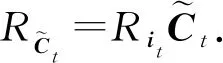
(22)

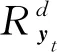
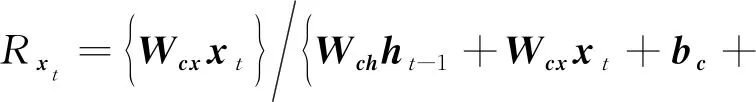
(23)

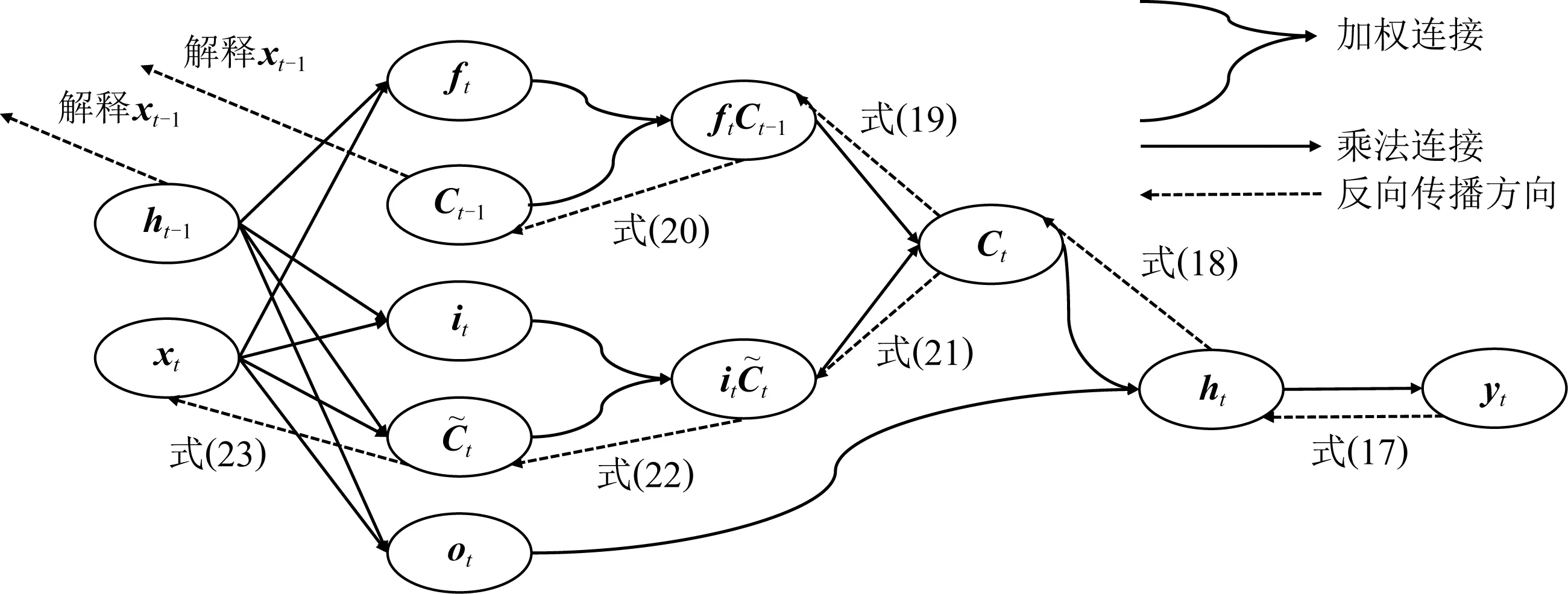
Fig. 6 The feedforward prediction path and the backpropagation path for interpreting its prediction results

2) 不确定性评估

Ding等人[45]和Hu等人[46]都使用不确定性评估方法解决可解释性差的问题，这里主要阐述前者的方法：通过为模型的每一个预测值y提供一个不确定性评分u(由模型输出)，以减轻预测过程中的不透明性，增加模型的可解释性.不缺定性分为2种：

① 随机不确定性(或数据不确定性).由随机事件或观测中的固有噪声导致.由于神经网络的固定权值，因此输入x的噪声会传播给输出y.用D表示噪声，则模型的输出为

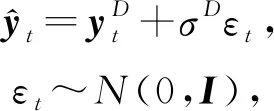
(24)

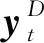
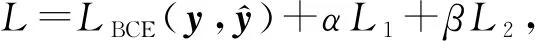
(25)

其中，L1,L2均为优化计算的正则项，由超参数α,β平衡权重.

② 认知不确定性(或模型不确定性).由数据不足导致，这种不确定性可以通过使用更多的数据来降低.针对深度学习模型的不确定性建模的贝叶斯方法是假设这些模型的权重不是固定的，而是从分布中取样的.最后的预测是通过综合所有可能的权重得到的.对于分类任务，预测正确的概率可以近似为

(26)

其中，c表示预测正确的题目，S表示取样总数.不确定性可以用熵概括：

(27)

2.1.3 小 结

本节详细介绍了DLKT领域针对可解释性问题的改进方法，主要分为Ante-hoc和Post-hoc.前者对问题的解决程度稍显不足，无论是注意力机制还是自解释模型都只能提高某一部分的可解释性.而后者试图解释整个模型，但其方法本身对部分条件要求较高，如LRP需要预测函数有较高的梯度.

2.2 针对长期依赖问题的改进

针对长期依赖问题的改进模型中，根据方法的不同，可以分为LSTM的扩展模型和基于自注意力机制的模型.

2.2.1 基于LSTM的扩展模型

1) Hop-LSTM

Abdelrahman等人[47]使用了Hop-LSTM来进一步扩大LSTM的序列学习容量.Hop-LSTM是一种改进的LSTM，可以根据隐藏单元之间的相关性进行跳跃连接.如图7所示，Hop-LSTM所基于的顺序关系为q1←q4,q2←q3,q5←q3,…,q4←qt，其中ft的计算参考式(8).可以看到，LSTM单元依据顺序关系跳跃连接.

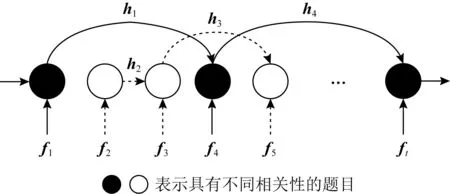
Fig. 7 Hop-LSTM schematic diagram

2) NKT(neural KT)

有研究指出，RNN的层层叠加可以减轻LSTM中长期依赖关系的学习困难[48].基于这个结论，Sha等人[49]提出了NKT模型，设计了一种2层堆叠的LSTM，并使用残差连接减小训练难度.实验证明，这种叠加的LSTM可以有效扩大序列学习的容量.

2.2.2 基于Transformer的模型

自注意力机制(self-attention mechanism)是注意力机制的一个变体，由Lin等人[50]提出.后来，Vaswani等人[51]使用自注意力机制代替了RNN搭建了整个模型框架，提出了Transformer模型.由于Transformer模型不依赖RNN框架，因此不存在长期依赖问题.Transformer模型最初用于机器翻译任务，取得了很好的效果.后来，有研究者将其用于知识追踪领域，获得了媲美基于RNN的DLKT模型的效果，且不存在长序列依赖问题.

1) SAKT(self attention KT)

Pandey等人[52]率先在知识追踪领域使用了Transformer模型，提出了SAKT模型，其结构如图8所示：

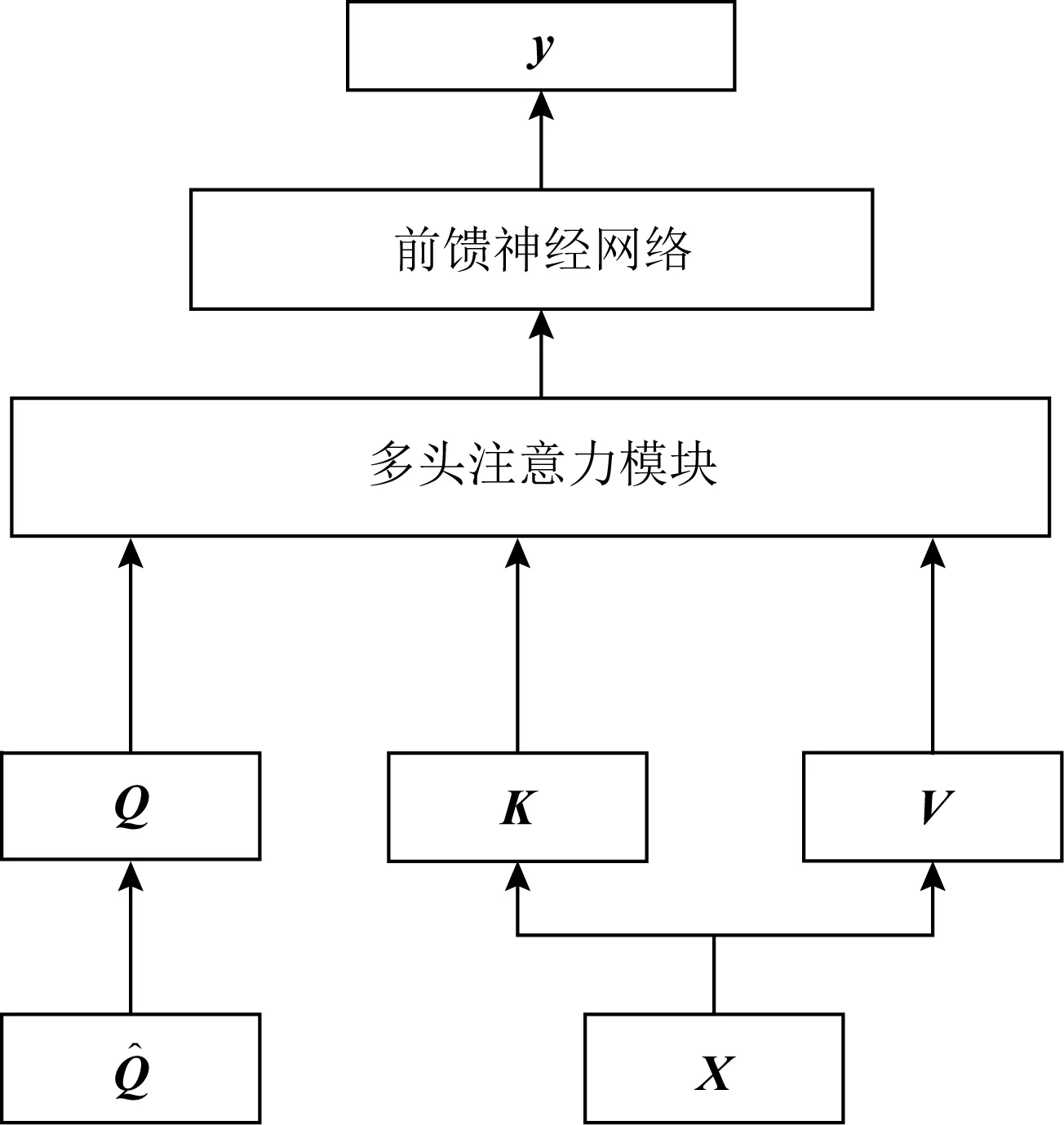
Fig. 8 Architecture for SAKT model

在Transformer中，计算注意力所使用的Q,K,V这3个参数由输入序列乘以不同的权重矩阵所得.而在SAKT中，Q和K,V分别由题目的嵌入序列和交互的嵌入序列投影得到.

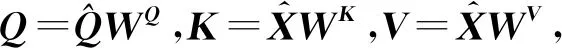
(28)

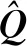
注意力被计算h次，使得模型能够在不同的表示子空间中学习相关信息，并将h次的结果连接,称为多头注意力(multi-head attention, MHA)：

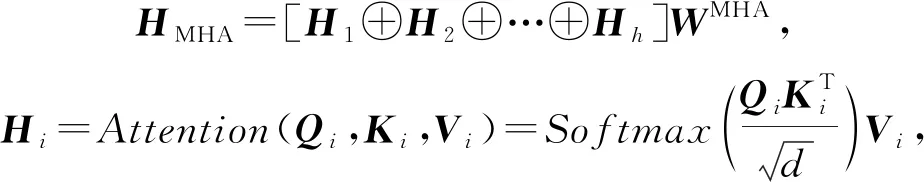
(29)

其中，d为嵌入向量的维度.最终，通过一个前馈神经网络层和一个Sigmoid激活的线性层得到预测结果：

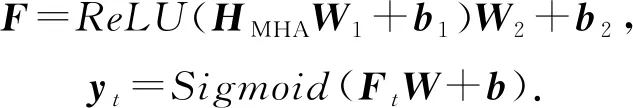
(30)

2) SAINT(separated self-attention neural KT)

Choi等人[53]认为SAKT模型的注意力层太浅，且Q,K,V的计算方法缺乏经验支持，并提出了SAINT模型以解决这2个问题.

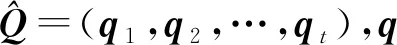
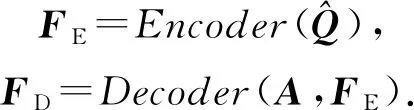
(31)

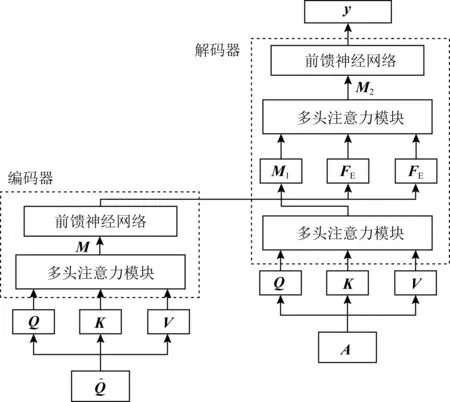
Fig. 9 Architecture for SAINT model

编(解)码器的内部实现与SAKT相同，最终，解码器的输出FD经过一个Sigmoid激活的线性层得到最终的预测结果.

在SAINT中，编(解)码器共叠加了4层，实验结果证明，多次叠加的注意力层可以有效增大AUC的面积，获得更好的预测性能.

3) DKT+Transformer

Pu等人[54]改进了Transformer的结构，在其中加入了题目的结构信息和答题的时间信息.改进后的Transformer模型结构与SAINT大致相同，都由编码器和解码器组成，主要区别在于自注意力的计算.

(32)

其中，t′=(t1,t2,…,tn)为时间戳信息，注意力机制的计算为：

(33)

其中，b×(tj-ti)表示时间间隔偏置，目的是通过xj与xi之间的间隔时间来调整注意力权重，在计算时，使i≤j以保证不会学习后面时间的权重.

2.2.3 小 结

本节详细介绍了DLKT领域针对长期依赖问题的解决方法，主要分为基于LSTM的方法与基于Transformer的方法.前者在一定程度上扩展了RNN序列学习的长度，但是并没有从根本上解决问题.后者不存在长期依赖问题，但是也丧失了RNN对序列建模的能力，位置嵌入对序列信息的影响更是需要深入研究.

2.3 针对缺少学习特征问题的改进

针对缺少学习特征问题的改进中，根据特征添加方式的不同，可以分为嵌入方式、损失函数、新结构3种方法.

2.3.1 嵌入方式

嵌入方式指将学习特征添加到模型的输入嵌入向量中，或作为额外的计算因子嵌入到计算过程中的方式.

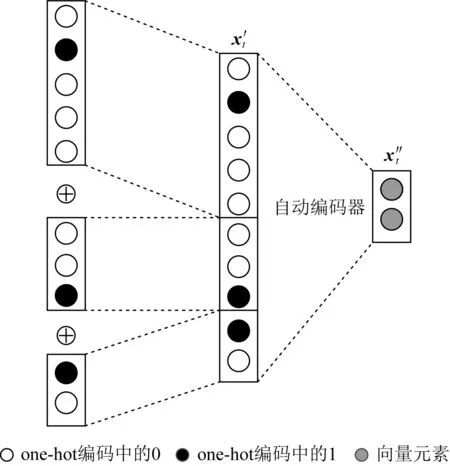
Fig. 10 Concatenate feature vectors and reduce dimensions

1) DKT-FE(DKT with feature engineering)

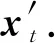
2) DKT-DT(DKT with decision trees)

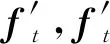
(34)

3) DKVMN-DT(DKVMN with decision trees)

Sun等人[59]基于DKVMN模型添加特征，提出了DKVMN-DT(DKVMN with decision trees)模型.其使用了与DKT-DT相同的方法，不再赘述.

4) DKT+forgetting

Nagatani等人[60]在DKT模型中加入了遗忘特征.作者用3点信息衡量学生的遗忘情况，如图11所示，分别是相同题目时间间隔、相邻题目时间间隔和题目历史练习次数.

Fig. 11 Three measures of forgetting

使用one-hot编码衡量遗忘的3种因素，然后连接，得到一个multi-hot编码的遗忘因子ct.如图12所示，遗忘因子作为额外的特征，分别与交互嵌入xt和隐藏状态ht整合.

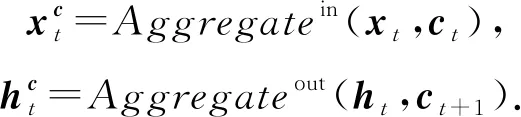
(35)

5) EERNN(exercise enhanced RNN)

Su等人[40]关注到题目文本描述中包含的丰富信息，并使用双向LSTM提取文本描述的语义特征.如所图13所示，题目的文本描述被表示为单词序列并使用Word2Vec[61]将转化为向量序列(w1,w2,…,wm)，作为双向LSTM的输入.然后，训练之后，连接前向状态和后向状态，经过一个逐元素的最大池化操作，得到最终的语义表示e.语义表示作为题目的嵌入，与答案组合成新的交互嵌入，作为LSTM的输入.

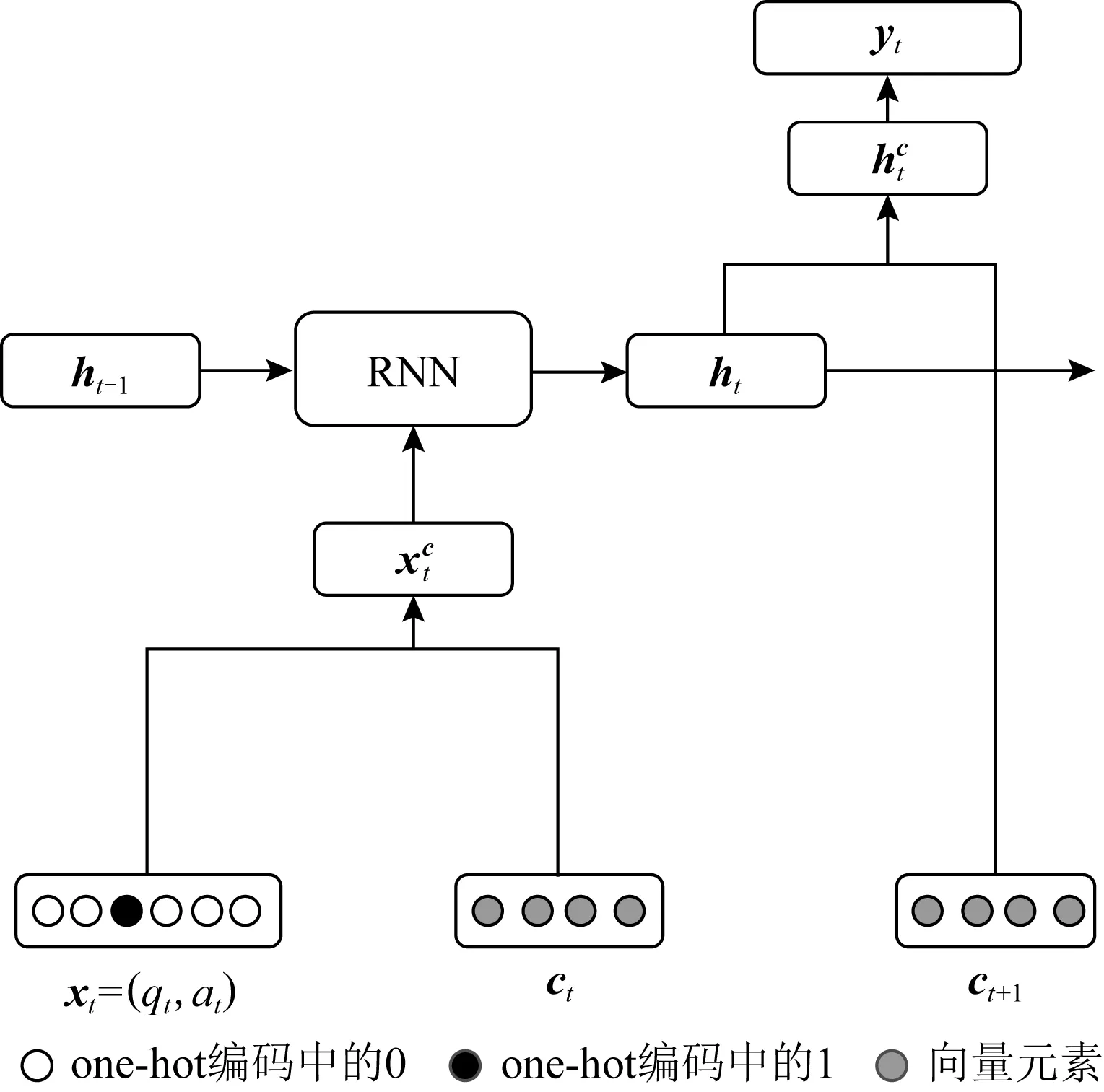
Fig. 12 The addition of forgetting features

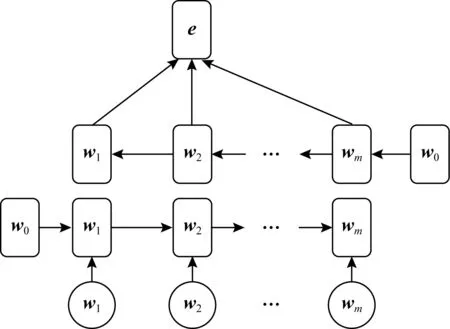
Fig. 13 The bidirectional LSTM is used to extract semantic features

6) AKT(adaptable KT)

Cheng等人[62]在其模型AKT中使用了与EERNN模型[27]相同的文本特征提取方法，并进一步从提出的语义特征中挖掘出学生的猜测(掌握了KC却没有答对题目)和失误(没掌握KC却答对了题目)行为.

在AKT中，猜测gt和失误st分别用单层神经网络建模：

st=S(et),gt=G(et).

(36)

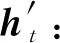
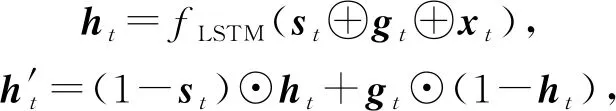
(37)

其中，fLSTM代表LSTM模型,⊙表示逐元素相乘.最后，模型根据知识状态做出预测.

此外，AKT还利用了迁移学习的思想，通过额外的自适应层一定程度上解决了数据稀疏问题.相比纳入专家知识[63]，这种方法具有更好的泛化性.

7) EHFKT(exercise hierarchical feature enhanced KT)

Tong等人[5]在其模型EHFKT中使用了BERT[64]从题目的文本描述中提取了知识分布、语义特征和题目难度等信息.如图14所示，EHFKT首先使用BERT生成文本描述的嵌入向量，然后经过知识分布提取系统(knowledge distribution extraction system, KDES)、语义特征提取系统(semantic feature extraction system, SFES)和题目难度提取系统(difficulty feature extraction system, DFES)分别生成知识分布、语义特征和题目难度.3个特征连接之后经过LSTM的输入作出预测.

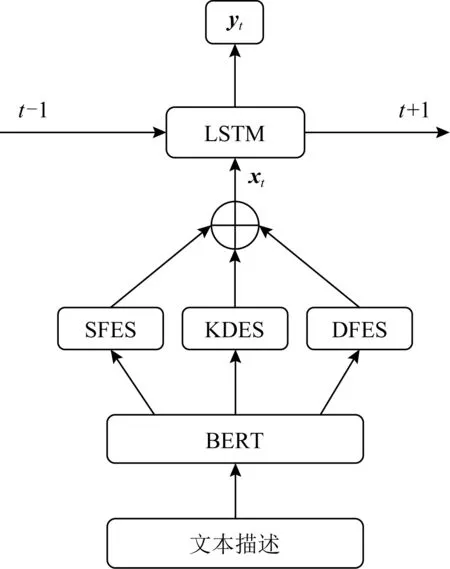
Fig. 14 Architecture for EHFKT

8) LSTMCQ(LSTM based contextualized Q-matrix)

Huo等人[65]在其模型LSTMCQ中提出了一种带有上下文信息的题目编码方法.具体来说，首先由领域专家手动创建一个矩阵Q，矩阵Q中存储了题目与KC的对应关系.迭代更新矩阵Q以附加KC的权重信息，且同一个问题的所有权重相加为1，记为权重矩阵Q.最后，加入学生n在题目m上的表现信息rnm：

(38)

其中，N,M分别为学生和题目的数量.qmk为题目m中KCk所占的权重(即权重矩阵Q第m行第k列的值)，δk表示学生在k上的平均表现.将δk与qmk相乘就得到了矩阵CQ(contextualized Q-matrix)对应的值：

CQmk=δk×qmk.

(39)

矩阵CQ包含了上下文信息，其每一行表示一个题目，将矩阵CQ的每一行单独提取出来，即为带有上下文信息的题目编码.

9) DKT-DSC(DKT with dynamic student classification)/DSCMN(dynamic student classification on memory networks)

Minn等人[66-67]提出了一种根据能力分类学生，并将分类后的学生分组训练的方法，相当于在模型的输入中隐式地嵌入了学生能力信息.应用于DKT与DKVMN，分别称为DKT-DSC和DSCMN.

具体来说，首先通过设置一个时间间隔将交互序列分段，在每一个时间间隔，计算学生每个KC的答对率和答错率，并将两者之间的差值转化为数据向量，以代表学生的能力：

(40)

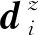
然后，用K均值(K-means)算法将学生按能力分组：

(41)

其中，μl为第l组(共m组)学生Cl的学习能力的均值.最后，将学生数据按照不同的分组放入模型中训练.

2.3.2 损失函数限制

损失函数限制指将额外的学习特征作为限制条件，编码到损失函数中的方式.

1) Colearn

Chaudhry等人[68]关注到了学习交互系统中学生的提示获取(hint-taking)行为，并将其作为知识追踪的子任务，提出了一个多任务模型Colearn.Colearn基于DKVMN模型，所不同的是，Colearn在更新知识状态矩阵Mvalue时，额外添加了gt(指示是否使用了提示)，新的输入(qt,at,gt)用one-hot编码为向量ft.Colearn的输出有2个，答对的概率y和请求提示的概率yg：

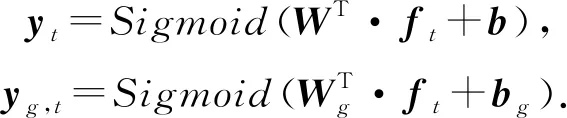
(42)

对应地，模型的损失函数也由知识追踪任务和提示获取任务2部分组成，并用超参数α,β平衡权重：

(43)

2) PDKT-C(prerequisite-driven DKT with constraint modeling)

Chen等人[69]将KC之间的先后序关系引入了知识追踪模型，提出了PDKT-C模型.以P(mi,k,t=1)表示学生i在时刻t掌握KCk的概率，假设k1,k2存在先后序关系，将KC之间的关系建模为有序对，可以表示为

P(mi,k2,t2=1)≤P(mi,k1,t1=1).

(44)

这个有序对很自然地说明了一个事实：一个知识点越先进，学习起来就越困难.在式(45)的约束下，经过正则化后，PDKT-C模型的损失函数为

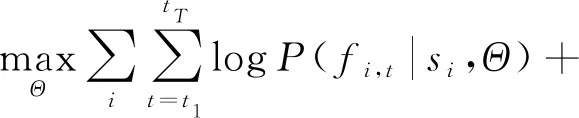
(45)

其中，si表示学生i的练习序列，Θ指代GRU的参数，fi,t指示学生i在时刻t是否回答了问题.第1部分为最大化似然函数.当fi,t1=fi,t2时，δ(*)=1，否则为0，α为平衡先决关系权重的超参数.

3) DKT-S(DKT with side information)

Wang等人[70]提出了DKTS模型，通过在加入一个用来捕获题目之间关系的Side Layer，将题目之间的关系纳入学生知识状态建模.

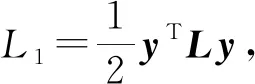
(46)

4) DHKT(deep hierarchical KT)

Wang等人[73]关注到了题目之间的层次结构关系，提出了DHKT模型.其通过KC嵌入和题目嵌入之间的内积铰链损失(hinge loss)来对层次关系建模.题目ei与KCkj之间的铰链损失定义为

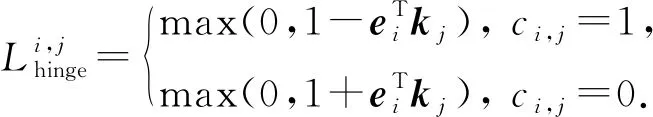
(47)

其中，ci,j=1表示ei与kj相关，反之无关.

在模型的训练过程中，同时最小化预测损失和铰链损失：

(48)

5) qDKT(question-centric DKT)

包含同样KC的题目之间存在着差异，解决这些题目对知识状态的贡献也是不同的.为了区分这些差异，Sonkar等人[74]提出了qDKT模型，使用正则项对题目之间的差异建模：

(49)

其中，c=(c1,c2,…,cn)包含了所有n个题目的正确率(通过数据集计算)，如果qi,qj包含同一个知识点，则1(i,j)=1，否则为0.这个正则项被加到模型的损失函数中作为限制：

(50)

2.3.3 新结构

新结构指通过使用新的模型结构，将额外学习特征纳入模型计算过程中的方式.

1) GKT(graph based KT)

Nakagawa等人[75]提出了GKT模型，通过将KC间的关系表示为1个有向图，知识追踪任务转化为了图神经网络(graph neural network, GNN)中的时间序列节点级分类问题.有向图G=(V,E,A)由节点集(表示KC)V={v1,v2,…,vN}、边集(表示KC之间的关系)E⊆V×V和邻接矩阵(定义关系的权重值)A∈N×N定义.

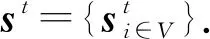
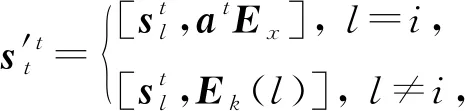
(51)

其中，Ex,Ek分别为交互和KC嵌入矩阵，Ek(l)表示Ek的第l行.根据图结构更新知识状态：

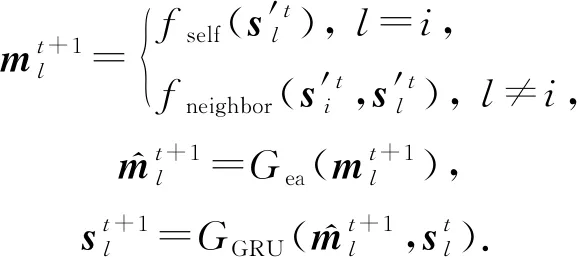
(52)

其中，fself为多层感知机，Gea为DKVMN模型中的删除-添加机制，GGRU为GRU模型，fneighbor为一个基于图结构信息向邻接节点传播的函数.

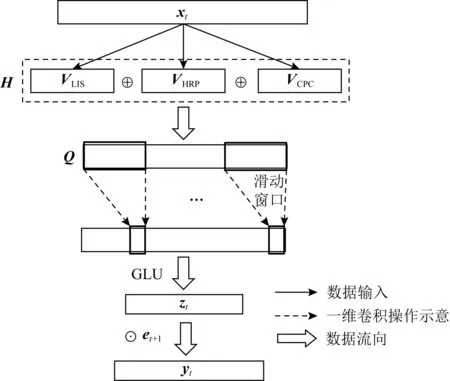
Fig. 15 Architecture of CKT model

2) CKT(convolutional KT)

Shen等人[76]提出了CKT模型，率先在知识追踪领域使用了卷积神经网络.如图15所示，在CKT中，使用1维卷积操作从矩阵Q中提取学习率特征，滑动窗口将d个连续的学习交互映射为单个输出元素，并使用GLU[77]作为非线性函数，在卷积层的输出上实现一个简单的选通机制，控制知识在学习过程中是否会被遗忘.最终的输出zt作为学生的知识状态，用于知识追踪的预测任务.

yt=Sigmoid(zt·et+1).

(53)

矩阵Q由学习交互序列(learning interaction sequence, LIS)、历史相关表现(historical relevant performance, HRP)和KC的正确率(concept-wised percent correct, CPC)在合并之后经过GLU单元[77]组成：

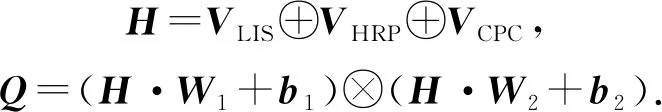
(54)

其中，⊗表示逐元素的乘法，VHRP,VCPC计算为

(55)

其中，Masking为掩码操作，目的是排除后续时刻的学习交互，qk为与KCk相关的题目，count(qk)表示qk被回答的次数.

3) SKVMN(sequential key-value memory networks)

Abdelrahman等人[47]在SKVMN模型中使用三角隶属度函数(triangular membership function)来计算KC之间的相关性：

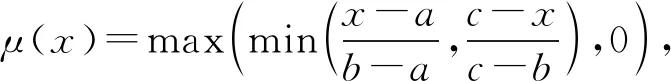
(56)

其中，a,c确定三角形的“脚”，b确定三角形的“峰”.

相关性用来进一步计算题目间的顺序依赖关系，并作为Hop-LSTM的约束，控制信息在其上的跳跃连接,如图7所示.

4) DeepFM(deep factorization machines)

Vie[78]率先将DeepFM算法[79]应用到知识追踪领域，其优势在于对稀疏特征的添加与利用.DeepFM由FM和DNN(deep neural network)组成，前者的输出为

(57)

其中，wi为偏置值，N表示特征数量，fi表示第i个特征，vi表示系数矩阵V的第i维向量，表示向量点积.

DNN是一个N层的前馈神经网络，其输出为

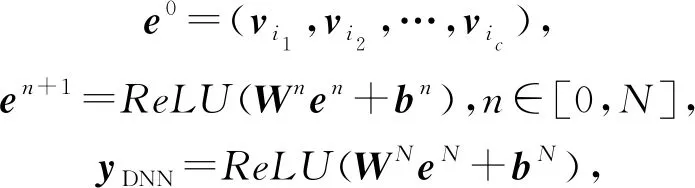
(58)

其中，c表示类别.DeepFM的预测由2部分组合得到：

y=Sigmoid(yFM+yDNN).

(59)

5) KTM-DLF(knowledge tracing machine by modeling cognitive item difficulty and learning and forgetting)

Gan等人[80]提出了一种结合学习者能力、认知项目难度、学习和遗忘等特征的建模方法，并使用KTM在高维中嵌入这些特征，所提出的模型称为DKM-DLF.

具体来说，Gan等人[80]认为，题目的难度包括3个方面：题目所包含的KC的难度、学习者的知识状态、题目的特点.综合这3个因素，题目难度被概括为认知项目难度(cognitive item difficulty, CID).设βk为KCk的固有难度，δj指代题目特点，KC(j)为题目j中包含的所有知识点，θ为偏置值.则对于学生i在时间t作答的题目j来说，其CID为

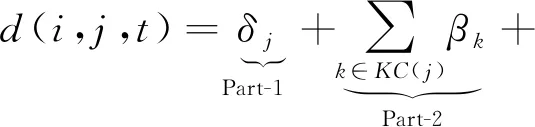
(60)

上述3个因素分别对应Part-1,2,3.其中，Ψ∈[0,c]代表难度，共c+1个等级，用之前交互中的回答错误率计算：

Ψi,v,t|v={j,k}=

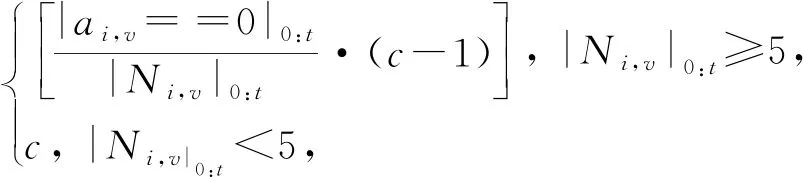
(61)

其中，|Ni,v|0:t表示学生i直到时刻t回答过的题目或KC.学生的学习特征通过其在相同题目Φi,j,t和包含相同KC的不同题目Φi,k,t上的表现计算：

(62)

无论回答的正确与否，都有助于知识的获得：

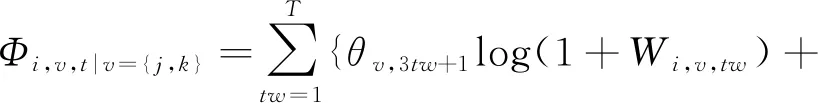
(63)

其中，Wi,v,tw与Fi,v,tw分别指代答对次数和答错次数，Ai,v,tw表示学生i在时间窗口tw的尝试次数，tw|0:T是跨度不断增大的时间间隔.

学习某个知识点的间隔越长，遗忘的可能性越大，将遗忘行为定义为

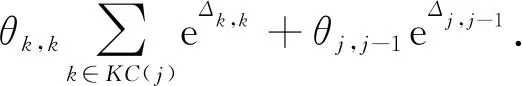
(64)

其中，e为自然对数的底，Δ为衡量遗忘的因素，有3个部分，与DKT+forgetting(图11)中提到的略有不同，具体如图16所示:

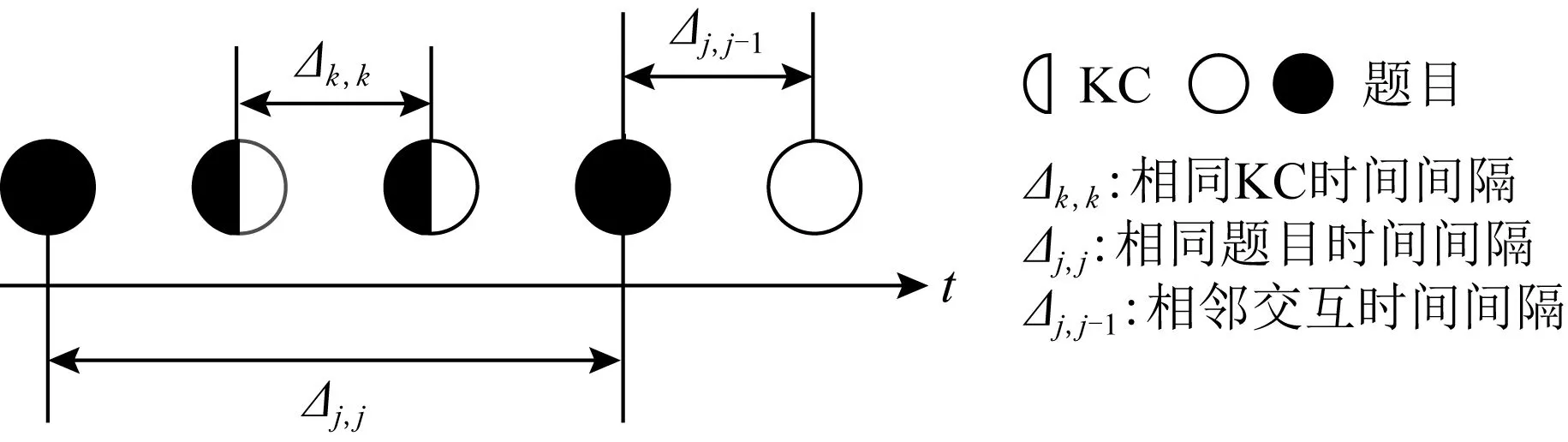
Fig. 16 Three measures of forgetting

设嵌入维度为0，用αi,j表示学生i在时刻t的能力，KTM-DLF模型可以表示为

Sigmoid(P(Yi,j,t=1))=αi,t-d(i,j,t)+l(i,j,t)-f(i,j,t).

(65)

6) DynEMb

Xu等人[81]结合了矩阵分解和RNN，提出了DynEmb模型，用矩阵分解做嵌入，用RNN对学习过程建模，DynEmb主要分为2部分：.

① QuestionEmb.给出学习交互，用矩阵分解学习题目嵌入矩阵Q和学生嵌入矩阵S：

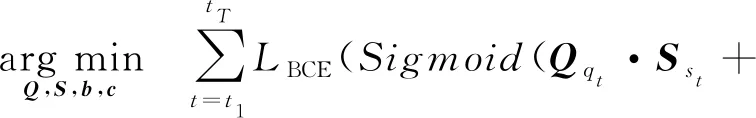
(66)

其中，b,c分别为题目和学生的偏置项，λ为平衡参数.

② StudentDyn.使用RNN生成动态的学生嵌入矩阵St.在时刻t-1，RNN的输入为题目嵌入Qqt-1和向量(at-1,1-at-1)T的克罗内克积(Kronecker product)，RNN的隐藏状态就是学生st的动态嵌入Sst,t.DynEmb预测下一时刻答对题目的概率：

yt=Sigmoid(Qqt·Sst,t+bqt).

(67)

7) BDKT(Bayesian neural network DKT)

Li等人[82]提出了BDKT模型，使用贝叶斯神经网络来对丰富的学习特征建模.BDKT的参数设置为分布形式：

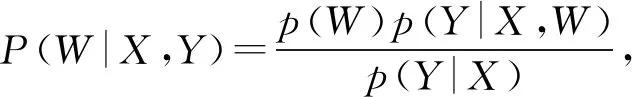
(68)

其中，X,Y分别为输入和输出，p(W)为参数W的先验.由于P(W|X,Y)在训练集(X,Y)上的概率分布是复杂的，难以用归一化常数处理，也不能直接计算模型参数的后验分布.BDKT使用了变分推断(variational inference)解决这个问题，变分分布q(W)～N(W|μ,σ2)被用来近似真正的后验分布P(W|X,Y)，N(μ,σ2)表示数学期望为μ、方差为σ2的正态分布.p,q之间距离为

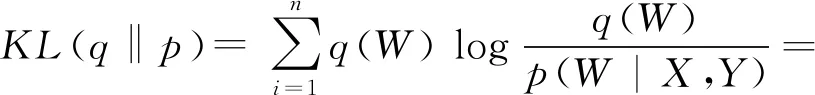
(69)

其中，Eq[logp(Y|X)]为常量，Eq[logp(Y|X,W)]可以从训练集中得到.BDKT的损失由训练损失和KL项决定：

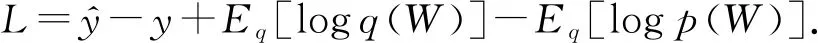
(70)

8) Q-Embedding

Nakagawa等人[83]提出了无需KC标签信息的Q-Embedding模型，可以自动学习题目与KC的嵌入.

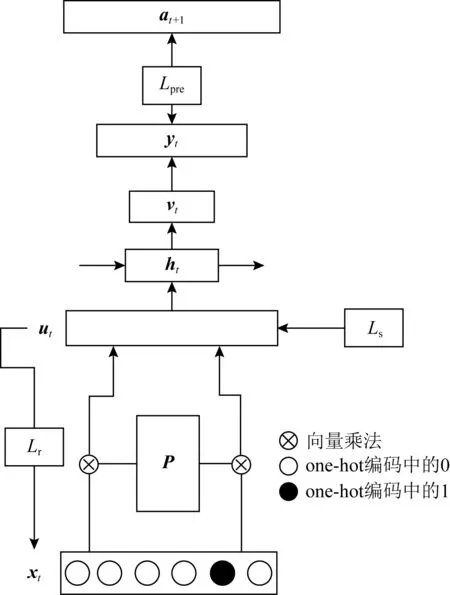
Fig. 17 Architecture of Q-Embedding model

Q-Embedding模型的结构如图17所示，其中，P为需要学习的题目-KC矩阵，ut与vt为额外的隐藏层，长度分别为2N′和N′，N′为自定义的KC个数，ut,vt,P的定义为

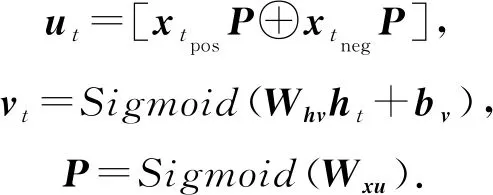
(71)

式(71)中，xtpos,xtneg分别表示xt的前后2部分，ht为RNN的隐藏状态.使用2个额外的损失函数对模型进行训练：

(72)

其中，Lref为对题目空间和KC空间的重构正则化，旨在反映以下假设：从学生对KC空间对应的每个KC的理解中，可以估计出学生对题目的回答情况.Ls为题目嵌入矩阵的稀疏正则化，目的是在训练模型后二值化时使P接近0或1，并抑制信息丢失.Q-Embedding的损失函数分为3部分，预测的交叉熵Lpre,Lref，Lspa，用超参数α,β,γ平衡权重：

L=αLpre+βLref+γLspa.

(73)

2.3.4 小 结

本节详细介绍了DLKT领域针对缺少学习特征问题的改进方法，主要分为嵌入方式、损失函数限制和新结构.其中，嵌入方式的最为直观：通过添加更多信息，借助深度学习的特征提取能力，使模型自主地建立特征间的联系.损失函数将额外信息作为一种限制条件，使模型向指定方向优化.新结构方式则充分利用了其他网络结构的特点，带来了许多优点(如预防过拟合[82]、减轻数据稀疏问题[62]等)，但新结构的迁移应用研究不够深入，其可能存在的缺点值得更进一步研究.

3 DLKT模型对比与分析

第2节详细介绍了DKT模型的改进方法，按照改进侧重点的不同，分为可解释问题的改进、长序列依赖问题的改进、添加特征的改进和其他方面的改进.本节归纳了各类改进方法中所使用的数据集，同时也对DLKT在各公开数据集上的表现做了对比和分析.

3.1 数据集介绍

近年来，用作DLKT模型评估的公开数据集主要有9个，其简述和下载链接如表2所示：

Table 2 DLKT Domain Public Datasets Summaries, Download Links and Models that Use Them

3.2 模型对比与性能概览

表3总结了各种模型所属的改进方向类别和其主要的改进方式.表4总结了使用公开数据集的DLKT模型的性能表现(以大多数论文都采用了的AUC指标为基准)，表4中的数据皆来自于模型初始论文，取最大值.需要指出的是，深度学习模型受参数设置影响较大，且同一个模型在不同论文中的表现也存在较大差异，因此，表4中的数据参考价值大于实际意义.

Table 3 An Overview of DKT Model Improvement Methods

Table 4 An Overview of DLKT Models

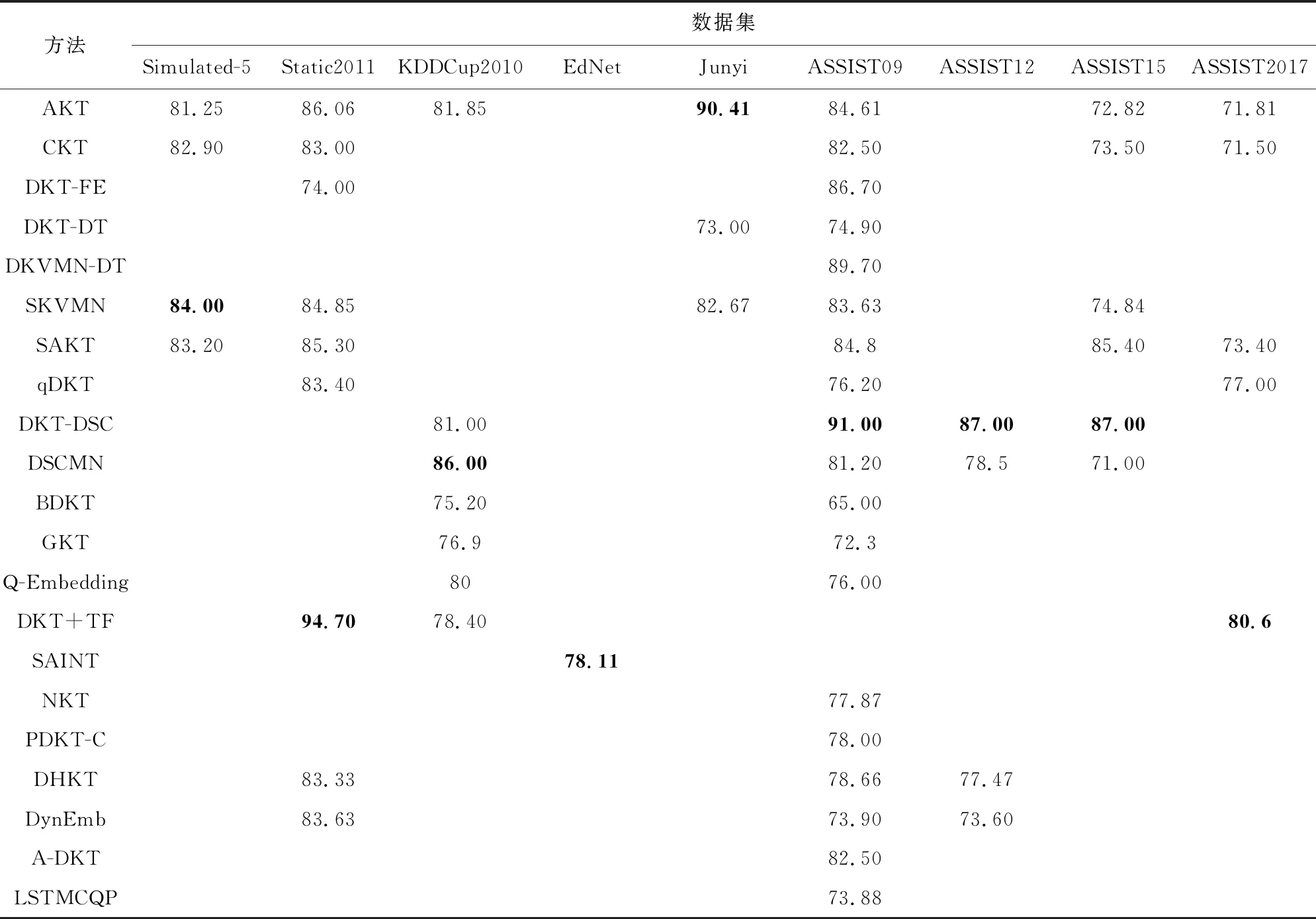
续表4 %

4 DLKT模型的应用

在DLKT领域，除了对DKT模型的改进之外，还有许多研究致力于探索DLKT模型在教育领域的应用.如图18所示，除了主要用来预测学生下一次答对题目的概率，DLKT模型还有许多其他应用，下面简单介绍这些应用.

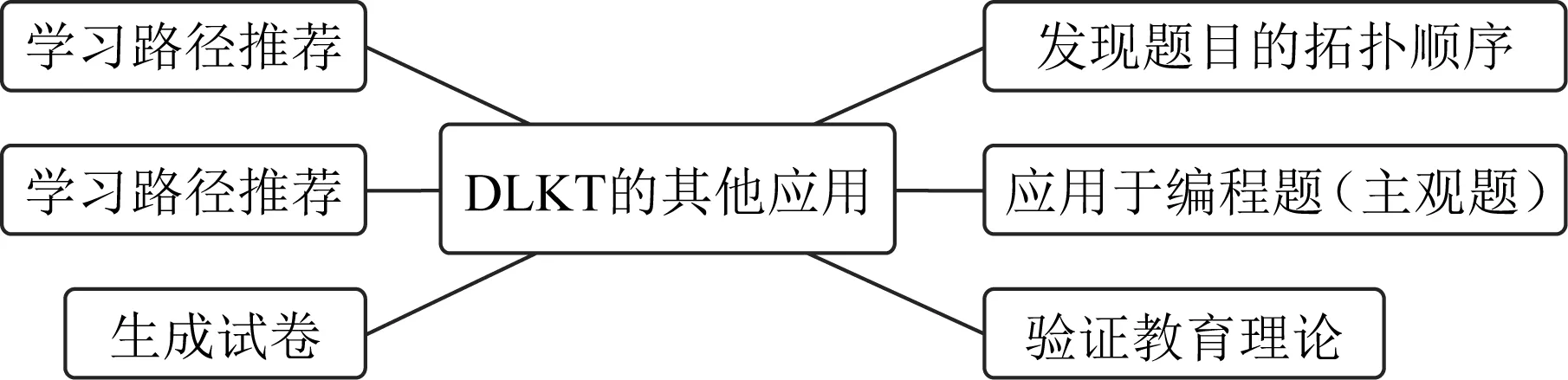
Fig. 18 Other applications of DLKT model

4.1 发现题目的拓扑顺序

Zhang等人[84]提出了一种基于规则的方法，利用DKT模型发现知识点之间的拓扑顺序.具体来说，在DKT模型中，由于一个题目对应一个知识点，因此，答对题目的概率可以视为掌握题目对应知识点的概率.将输出概率大于0.5的知识点视为掌握，拓扑顺序的发现分为3个步骤：

1) 确定偏序关系.若当前的知识点被掌握，则输出概率最高的知识点为先决知识点；若当前的知识点未被掌握，则输出概率最低的知识点为先决知识点.

2) 删除冗余连接.设ka,kb,kc为存在ka→kb,kb→kc,ka→kc关系的3个KC，删除其中的冗余连接，得到类似ka→kb→kc的有向无环图.

3) 用Kahn’s算法[85]把有向无环图转化为拓扑顺序.

4.2 应用于编程题(主观题)

Wang等人[86]将LSTM模型应用到编程题上，模型的输入为学生对单个编程题目的多次提交记录.提交的代码被表达成一个抽象语法树(abstract syntax tree, AST)，然后利用递归神经网络对代码的AST进行向量化[87-88]，向量化后的AST作为LSTM的输入，最后，模型预测学生能够成功解决同一个知识点的下一个编程题的概率.Wang等人[86]的模型仅支持基于块的编程语言Scratch，Swamy等人[89]扩展了他们的工作，提出了一种对编程语言没有限制的模型.在模型的输入方面，Swamy等人使用了scikit-learn的默认标记方案对学生代码中的非字母数字字符做分词，然后计算词频-逆文档频率(term frequency-inverse document frequency, tf-idf)生成代码的向量表示.向量的长度为单词的总数，其中每一项为对应单词出现的次数.代码的向量化表示与one-hot编码的学生编号、问题编号、尝试次数编号组合，作为LSTM的输入，模型的预测结果为完成每个知识点对应题目的剩余尝试次数.

4.3 验证教育理论

Lalwani等人[90]利用DKT模型验证改进的布鲁姆分类法(revised Bloom’s taxonomy).改进的布鲁姆分类法将认知分为6个阶段，分别是记忆、理解、应用、分析、评估和创造.这6个阶段的复杂度逐渐递增，且前面的阶段是后面阶段的先决条件.Lalwani等人[90]将验证过程抽象为研究掌握前面阶段的KC对掌握后面阶段知识点的影响.具体来说，通过模型的输出判断学生是否掌握KC，然后计算不同阶段KC之间掌握程度的差异：

(74)

在后续的工作中，Lalwani等人[91]在原始的DKT模型中加入了学生练习之间的时间间隔作为特征，将改进后的模型命名为DKT-t通过比较DKT与DKT-t模型的差异，研究时间间隔对预测的影响，并进一步利用DKT-t模型追踪遗忘曲线.

4.4 学习路径推荐

Cai等人[92]提出了一种利用知识追踪以及强化学习技术的学习路径推荐方法，并命名为KT-KDM.KT-KDM分为2部分，KTM和DKM，前者是一个基于DKT+模型的知识追踪模型，后者通过预测知识需求水平(level of knowledge requirements, LKR)来获得KTM提供的学习者知识掌握程度，并推荐习题.

如图19所示,推荐过程被建模为一个采用强化学习方法的Markov决策模型.KDM本质上是一个使用KTM建模的学习状态作为输入的预测网络，其输出为一个向量，其中每个元素表示每个习题的LKR.然后使用随机加权函数选择一个习题进行推荐.奖励函数设计为相邻2个推荐的习题的掌握度之差，同时，为了避免模型反复推荐相同的高回报习题，对已经推荐的习题进行了惩罚.奖励函数为

(75)

其中，k表示推荐的最后一个KC，sk,t表示k在时刻t的知识状态，nk,t表示在k被推荐的次数.

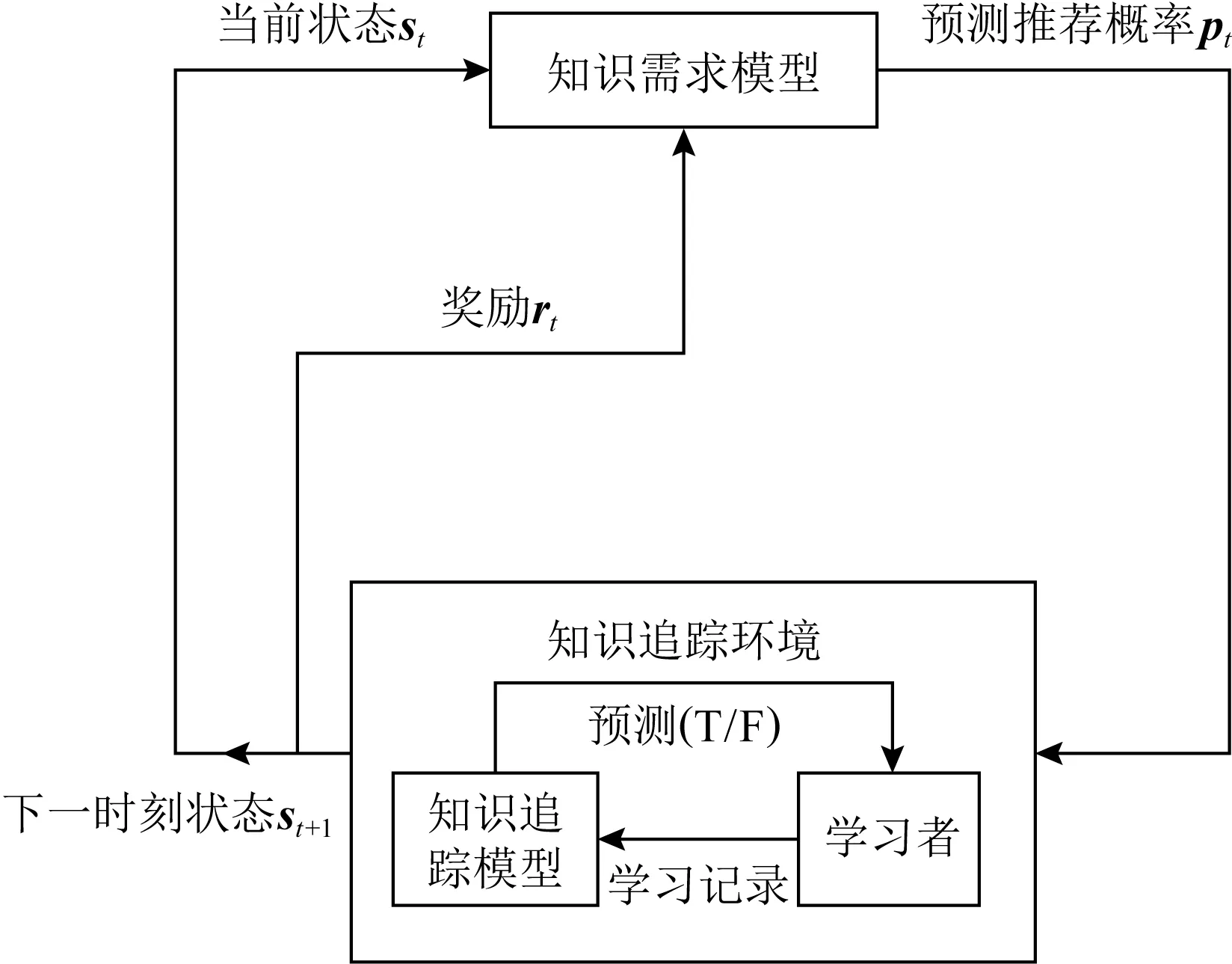
Fig. 19 Markov process model the recommendation learning path

4.5 STEM/Non-STEM职业预测

Yeung等人[93]将DKT+模型预测的结果与从数据集中提取出的学生特征相结合，以预测学生是否会从事STEM类职业.

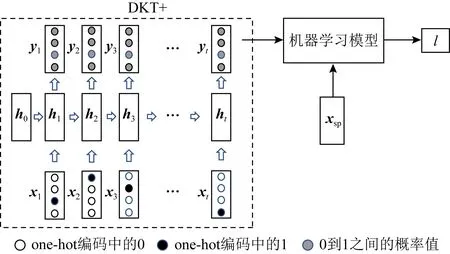
Fig. 20 Architecture of STEM/Non-STEM career prediction model

如图20所示，将DKT+模型最后一次预测的结果yt与学生的特征xsp连接得到x′=yt⊕xsp，作为机器学习模型的输入.机器学习模型学习x′与STEM标签l∈{0,1}的映射关系，并做出STEM/Non-STEM的职业预测，有GBDT，LAD，LR，SVM这4种实现方式.

4.6 生成试卷

Wu等人[94]提出了一种利用知识追踪的试卷生成方法.具体来说，假设一张试卷包含nq个题目与nk个知识点，则试卷可以表示为一个矩阵E∈nq×nk.使用每种知识点出现的概率表示试卷中每种知识点的权重，用P(oj)表示KCj出现的概率：

(76)

其中，Eij表示E的第i行第j列.假设有ns个学生，学生的对知识点的掌握程度可以表示为矩阵S∈ns×nk.知识掌握程度来自于深度知识追踪模型输出的答对题目的概率，由于一个题目对应一个知识点，所以答对题目的概率可以看作是对知识点的掌握程度.将题目中所有知识点的掌握程度相乘即为答对题目的概率，学生l答对题目i的概率P(ali=1)表示为

(77)

用Scorei表示问题i的总分数，则学生l的试卷成绩可以表示为

(78)

将ns个学生的成绩联合，表示为R={r1,r2,…,rn}，用P(R)表示R的分布.Wu等人提出，合理的试卷有2个必要条件：

1) 卷中KC分布与课程中的接近，即Φ～W.其中，Φ=(P(o1),P(o2),…,P(onk))，W中每一项表示对应KC的权重.

2) 每一组学生成绩的分布应该符合正态分布，即P(R)～N(μ,σ2)，其中，N(μ,σ2)表示均值为μ、标准差为σ2的正态分布.

最后，使用动态规划算法和遗传算法更新试卷，使其符合上述2个必要条件.

5 总结与展望

本文聚焦教育大数据中的知识追踪，对该领域内基于深度学习方法的知识追踪模型进行了全面回顾和系统性的梳理.首先介绍了该领域的开创性工作DKT，然后基于该工作，分针对可解释问题的改进、针对长期依赖问题的改进以及针对缺少学习特征问题的改进三大主要技术改进方向构建了技术演进脉络图、梳理了各模型的技术重难点、分析了各模型的优点和局限性.其中，可解释性问题作为深度学习领域普遍存在的问题，尚未得到有效解决，DLKT也不例外，目前的方法都只能有限地提高可解释性.长期依赖问题在自注意力模型上得到了完美解决，但其需要额外的位置编码才可以维持序列学习能力.对缺少学习特征问题的研究占据了DLKT的主要部分，嵌入方式、损失函数限制和新结构3种方式各有优劣：嵌入方式直观但是过于依赖模型的学习能力，损失函数限制可以使指定模型优化的方向但需要大量的人工工作，新结构的使用带来了许多优点，但深入研究的缺乏可能使其中的缺点无法暴露.最后我们还整理了可供研究者使用的公开数据集，对比评估了各模型的性能表现和考察了该领域的主要应用.

基于深度学习的知识追踪因其优秀的性能而被广泛关注.对于目前发展迅速的线上教育，其产生的大量教育数据正好对应了深度学习模型对于数据量的需求，而无需标注数据的特性大大提高了数据的利用率，同时，深度学习框架的普及降低了模型构建的门槛.多种因素的共同作用，使得DLKT被广泛应用于在线教育平台，也使其成为教育数据挖掘领域新的研究热点.但是目前该领域尚在起步阶段，在实际应用中，仍有许多挑战和问题亟待解决.基于目前存在的挑战与问题，我们总结了7个可能的研究方向供研究者参考.

1) 现有DLKT模型大多使用二元变量来表示题目的回答情况，这种建模方式不适合分数值分布连续的主观题.Wang等人[86]和Swamy等人[89]在处理学生的编程数据时，使用了学习者回答的连续快照作为回答情况的指示器，这提供了一种对主观题目建模的方式.而其他的对主观题目的建模方法仍有很大的研究前景.

2) 目前DLKT主要应用于在线教育平台，如何利用好在线平台所提供的大量学习轨迹信息，是研究的难点之一.Mongkhonvanit等人[95]提供了一种对教学视频观看行为建模的方法，Huan等人[96]则利用了鼠标轨迹信息.而其他学习特征信息的提取、建模亟需更多的研究.与此同时，特征的添加也是一大难点.对于以RNN为基础的DLKT模型来说，输入向量的长度会显著影响模型的训练速度.这就需要使用降维方法减小向量的长度，或者采用其他的嵌入方式(如LSTMCQ)融合更多特征而不增加向量长度.总而言之，学习特征信息的提取、建模、添加将会是DLKT实际应用中的重点研究方向.

3) DLKT的优秀性能使利用其验证经典教育理论成为可能.如Lalwani等人[90]验证改进的布鲁姆分类与遗忘曲线.同时，已提出的教育理论也可以为建模提供指导，如Gan等人[80]结合了学习与遗忘理论.经典教育理论在DLKT领域的应用值得更多的研究者加以关注.

4) 利用DLKT模型构建知识图谱.DLKT模型可以用来发现知识点之间的相互关系，构建出知识点关系图，这可以看作是简化的知识图谱.知识图谱作为当前人工智能时代最为主要的知识表现形式，如何扩展模型的知识结构发现能力，将知识点关系图扩展为知识图谱将会是未来的重点研究方向.

5) 目前的DLKT模型中仍存在许多不确定因素，现有的理论推断并不足以解释DLKT模型的训练过程.在基于Transformer的模型中，掩码机制被用来屏蔽后面时间的权重，这是为了防止未答的题目影响已答的题目.而Xu等人[97]使用双向LSTM以融合过去和未来的上下文序列信息.两者所依据的原理是相悖的，但都获得了性能提升.如何深入研究，以完整解释DLKT模型的训练过程，将会是未来的重点研究方向.

6) 目前DLKT主要使用RNN模型，许多研究已经证明了RNN的优越性.同时，Transformer模型、GNN模型也在知识追踪领域有着优秀的表现.而其他更多模型的应用仍亟需深度研究，对其他深度学习模型的应用将会是重要研究方向.

7) Transformer相对于RNN的一大优势就是没有长期依赖问题，但目前基于Transformer的DLKT模型却并没有利用好这个优势，如SAKT和SAINT，它们都将序列长度设置为100，这个长度并没有超过LSTM的序列学习容量(200).同时，实验显示，位置编码的有无对最终的结果影响并不大.这似乎说明长期依赖与序列关系对KT任务的影响没有目前所认为的那么大，以此类推，各种学习特征对于KT任务的影响值得进一步研究.

作者贡献声明：刘铁园、陈威是综述的主要写作人，完成相关文献资料的收集和分析、论文初稿的写作和校对；常亮、古天龙是项目的构思者及负责人，指导论文写作.