角接触球轴承布置对轴承的影响

王俊勤

(山西省机械产品质量监督检验站有限公司，山西 太原 030009)

0 引言

角轴承是指可同时承受轴向力和径向力的轴承类型，角轴承所能承受的轴向载荷随接触角增大而增大，反之，适用于高速旋转且径向承载能力强的角轴承对应的接触角越小。基于角接触球轴承刚性较好、高速性好、成本低等优点，高精度配对角接触球轴承常用于机床主轴并且带有预载荷[1-3]。轴承有DB背对背布置、DF面对面布置、DT串联布置三种不同的布置型式，另外也有可采用自由组配的万能组配型轴承。在制造业中，随着零件加工精度的提高，对机床的加工性能也提出了更高的要求[4]。其中，轴承的布置方式对轴承的力学性能有着重要的影响[5]。因此，本文对角接触球轴承的布置进行力学特性分析。

1 角接触球轴承单列背对背配列对轴承的影响

将两型号相同的角接触球轴承安装在芯轴上，配列形式为背对背，如图1所示。先施加预载荷Fp，两轴承均产生轴向位移δp。此时再施加轴向力Fa，轴承将产生轴向位移δa。

图1 单列背对背布置示意图

轴承1的轴向位移δ1由下式计算：

δ1=δp-δa.

(1)

轴承2的轴向位移δ2由下式计算：

δ2=δp+δa.

(2)

将式(1)和式(2)合并可得：

δ1+δ2=2δp.

(3)

在角接触球轴承轴向力Fa作用下，轴向位移δa和接触角α将发生变化，如图2所示。

图2 轴向位移与接触角变化示意图

图2中，SG为轴承A点到B点方向未受力前的曲率半径；向量AB1为轴承受力后曲率半径；δn为法向位移；δa为轴向位移；α为AB与垂直线之间的夹角；α′为AB1与垂直线的夹角。

从图2可以看出：在受接触变形的影响下，内圈滚道曲率中心B移动至B1，并产生轴向位移δa和沿接触面的法向位移δn，故可得出如下几何关系：

(4)

整理式(4)可得出：

(5)

由图2几何关系可知，法向趋近量δn的计算公式为：

(6)

轴向趋近量δa的计算公式为：

δa=(SG+δn)sinα′-SGsinα=SG(sinα′-sinα)+δnsinα′.

(7)

将式(6)代入式(7)中，得出：

(8)

将式(8)代入式(3)可得出：

(9)

又由图2可知：∠BCA可近似看作为直角，则△BB1C中∠CBB1=α′，BB1=δa，B1C=δn，则有：

δn=δasinα′.

(10)

将式(5)、式(10)进行整理可得：

(11)

将式(9)、式(11)进行整理可得：

(12)

由角接触球轴承的拟动力学分析理论公式[6]可知：

(13)

其中：Z为滚动体个数；Dw为滚动体直径；fm为内、外圈滚道曲率半径与滚动体直径之比平均值，为常数；γ、c为趋近量常数。

由图3轴承组轴向受力示意图可知轴向力Fa为:

图3 轴承组轴向受力示意图

Fa=F1-F2.

(14)

其中：F1与F2分别为轴承组在轴向外载荷作用时轴承1和2受到的轴向力。

将式(13)代入式(14)可得：

(15)

其中：α1与α′1分别为轴承1受力时AB、AB1与垂直线之间的夹角；α2与α′2分别为轴承2受力时AB、AB1与垂直线之间的夹角。

先对试验对象轴承组施加500 N的预载荷，然后对轴承组施加轴向外载荷Fa，根据公式(12)和公式(15)得出如图4、图5所示的轴向外载荷与接触角、轴向位移之间的关系。

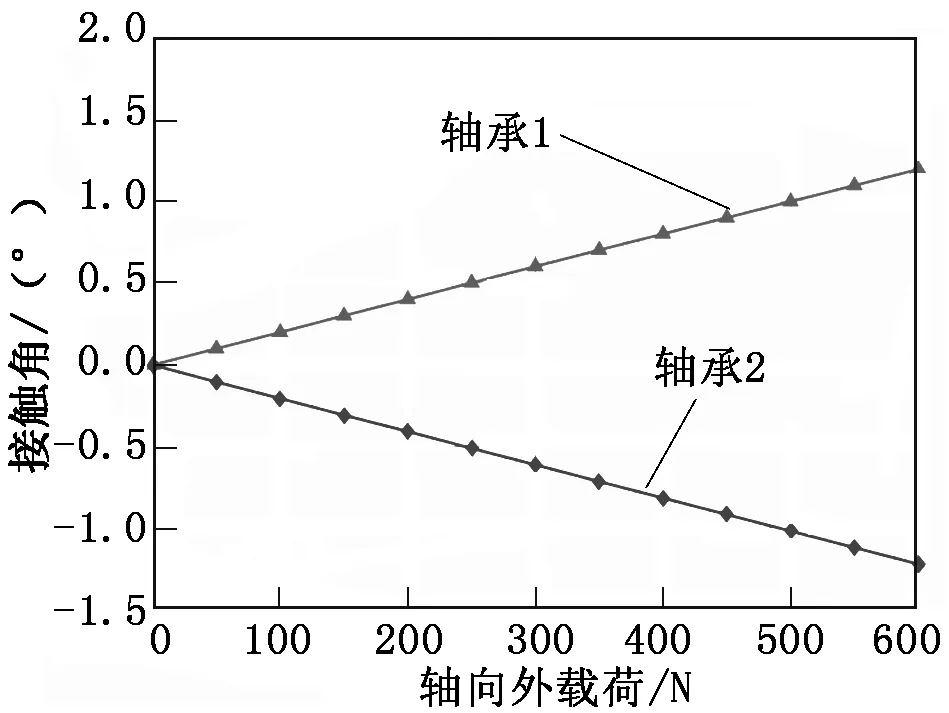
图4 轴向外载荷与接触角的关系

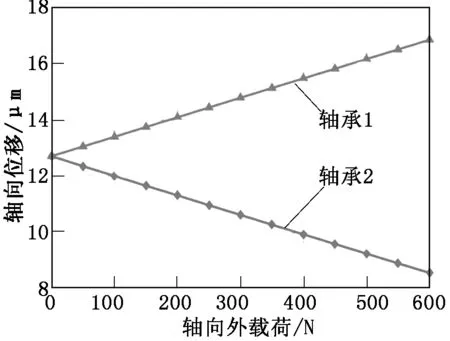
图5 轴向外载荷与轴向位移的关系

2 角接触球轴承双列配列对轴承的影响

双列轴承的布置方式有4种，分别是双列整体背对背、双列整体面对面、双列单端背对背、双列单端面对面，如图6所示。

图6 双列轴承的4种布置方式

在图6(a)或图6(b)布置方式和轴承类型相同的情况下，假定双排轴承与单排轴承承受的预紧力相同，单排轴承产生的位移为双排轴承各轴承位移的2倍，致使单列轴承的刚度相比较双列轴承的刚度更低。轴承组的极限转速会因为轴承数量的增加而下降。

此外，图6(a)布置方式虚应力点间距小于图6(b)布置方式。因此，背对背布置的稳定性相对较好。当采用图6(c)或图6(d)布置时，刚度计算与上述计算相似。但是，从轴向热变形的释放角度来看，图6(c)布置方式或图6(d)布置方式不如图6(a)布置方式。

3 结论

从图4、图5轴向载荷与接触角、轴向位移之间的关系可知：轴承1的接触角和轴向位移随着轴向载荷的增加而增加，轴承2的接触角和轴向位移随着轴向载荷的增加而减小。

在单列面对面布置情况下，轴承1所受的轴向力、接触角变化值、轴向位移随着外载荷的增大而减小；轴承2所受的轴向力、接触角变化值、轴向位移随着外载荷的增大而增大。这与单列背对背布置中的规律正好相反。

此外，这两种布置的虚受力点O1和O2的间距差距较大，使得面对面配列相比较背对背配列的主轴整体刚度较高、固有频率较大、回转精度较低。