阀门执行器箱体加强筋优化设计与分析*
2022-01-18鲁春艳
鲁春艳
(苏州市职业大学 机电工程学院,江苏 苏州 215100)
0 引言
阀门广泛应用于各种排水、通风、抽采、洒水等管道中,阀门执行器是用于控制阀门启闭的元件,当阀门执行器在爆炸极限工况下工作时,执行器箱体内压力会迅速增大,有可能导致执行器损坏,这对执行器箱体的抗爆性提出了要求[1]。
为了满足企业提高执行器性能和降低成本的要求,在原有产品的基础上对执行器进行优化设计。本文采用OptiStruct对执行器箱体进行拓扑优化,得到了爆炸极限工况下箱体的传力路径,根据拓扑优化的结果对箱体进行第一次设计,在箱体底部增加加强筋,有限元分析的结果表明,第一次设计满足使用要求。为了降低生产成本,对第一次设计的箱体进行基于响应面法的尺寸优化,并根据优化结果进行第二次设计。
1 原执行器箱体有限元分析
1.1 执行器箱体有限元模型的建立
执行器箱体原始结构如图1所示,箱体底部铸有蜗轮轴承座孔和蜗杆轴承座孔。在CATIA中建立执行器箱体的三维几何模型,再将该几何模型导入到ANSYS中,对执行器箱体模型进行几何清理,在不影响计算的情况下,可酌情去掉一些小特征,以简化网格。采用四面体进行网格划分,得到由583 842个节点和387 393个实体单元组成的有限元模型,如图2所示。执行器箱体材料为铸铝,泊松比为0.33,弹性模量为71 GPa,密度为2 770 kg/m3,屈服强度为255 MPa。

图1 执行器箱体模型 图2 执行器箱体有限元模型
1.2 边界条件的设置
执行器工作时,箱体固定不动,因此在箱体的端面施加固定约束;在爆炸极限工况下,执行器箱体承受2.5 MPa压力,因此在箱体内表面施加2.5 MPa的压强。执行器箱体的边界条件如图3所示。

图3 执行器箱体边界条件 图4 执行器箱体应力云图 图5 执行器箱体变形云图
1.3 计算结果分析
经过计算,执行器箱体的应力云图如图4所示。由图4看出:箱体内壁承受的压力均较小,最大处应力值为41.197 MPa;箱体内壁与箱体底面相接处一圈(显示黄色)受的应力都比较大,这说明在2.5 MPa的压力下,箱体底面承受较大的压力;最大应力值为136.02 MPa,发生在蜗杆轴承座与箱体底面相接处,应力最大值发生在此处是由于施加在箱体内部的压强所致。铸铝的屈服强度为255 MPa,箱体承受的最大应力值为136.02 MPa,考虑到2.0的设计安全系数,表明箱体的抗爆强度不足,且主要是底面承压强度不够。
执行器箱体的变形云图如图5所示,最大变形为0.180 46 mm,主要发生在蜗轮轴承座处,如果此处变形过大,会影响运动部件的功能。虽然此处的变形量还没达到设计极限0.2 mm,但仍可对箱体的刚度进行优化。
以上分析表明,执行器箱体的强度和刚度都有待加强。
2 执行器箱体拓扑优化设计
2.1 执行器箱体拓扑优化数学模型
拓扑优化是在约束条件下寻找部件的最佳布局形式或者最佳的传力路径,鉴于箱体底面强度不足,可采取加厚底面或者增加加强筋的方式进行加固。为了以最轻的质量寻得最佳的性能,拟对执行器箱体进行拓扑优化,根据优化后的结果来选择加固方式。
优化设计三大要素,即设计变量、约束条件和目标函数。设计变量是通过变量的变化来提高性能的一组参数;目标函数是需要求解的最优的性能目标,是关于设计变量的函数;约束条件是对目标函数的限制,是对设计变量和其他性能的要求[2]。
此次执行器箱体优化以材料单元密度为设计变量,以执行器箱体的刚度和体积分数为约束条件,以执行器箱体整体柔度最小为目标函数。设h(x)为总变形,g(x)为体积分数,p(x)为箱体柔度,则优化数学模型可表述如下:
设计变量:X=dev(desigh).
响应类型:h(x)=dis,
g(x)=vol,
p(x)=Compl.
约束条件:h(x)≤0.2 mm,
g(x)≤0.3.
目标函数:f(x)=min(p(x)).
其中:dev为单元网格密度变化;desigh为优化设计区域;dis为静力学位移;vol为体积分数;Compl为箱体柔度。约束条件为:质量分数上限30%,即保留材料不超过选定设计区域的30%;蜗轮轴承座孔变形量不超过0.2 mm;目标函数为柔度最小。
2.2 执行器箱体拓扑优化
由前面的分析可知,主要问题是箱体底部承压强度不足,因此将箱体底面设为设计区域,将箱体内壁、蜗轮轴承座、蜗杆轴承座等设为不可设计区域,利用Hypermesh建立执行器箱体拓扑优化模型,如图6所示。

图6 执行器箱体拓扑优化模型
采用变密度拓扑优化方法,根据图3添加边界条件,以材料密度为设计变量,以蜗轮轴承座变形量不超过0.2 mm、体积分数不大于0.3作为约束条件,以柔度最小为优化目标,对执行器箱体进行拓扑优化,得到的拓扑优化结构如图7所示。

图7 执行器箱体拓扑优化结构
由图7可知,轴承座孔四周与底部边缘四周的材料单元密度比较大,并予以保留,底面中部一圈材料单元密度较小,一部分材料单元已被去除。轴承座孔四周与底部边缘形成了十分清晰的放射状的传力路径,可采用加强筋的方式来对箱体底面进行加固[3]。
3 执行器箱体第一次设计与结果验证
3.1 执行器箱体第一次设计
根据拓扑优化结果对执行器箱体进行第一次设计,在对结构整体刚度贡献大的区域布置加强筋,在对结构整体刚度贡献较小的区域则无需布置加强筋。图7的放射状传力路径比较密,考虑到布局与实际加工的难度,将其简化成均匀布置的7根加强筋,加强筋截面采用比较容易加工的矩形,根据以往的设计经验,加强筋截面尺寸选择为宽6 mm、深5 mm。执行器箱体第一次设计结构如图8所示。

图8 执行器箱体第一次设计结构
3.2 结果验证
对第一次设计的执行器箱体进行强度、刚度分析。执行器箱体的应力云图如图9所示。由图9可知:最大应力发生在加强筋与箱体底面边缘相交处,最大应力值为112.97 MPa,考虑2.0倍的安全系数,仍小于铸铝的屈服强度255 MPa;由于加强筋的存在,底面强度得到了加强,蜗杆轴承座与箱体底面相接处的应力值降低到101.57 MPa,小于原执行器箱体的最大应力136.02 MPa。

图9 第一次设计箱体应力云图 图10 第一次设计箱体位移云图
执行器箱体的变形云图如图10所示,最大变形为0.122 95 mm,还是发生在蜗轮轴承座处,低于原执行器箱体的0.180 46 mm。
从以上分析可知,第一次设计的执行器箱体的强度和刚度均能满足使用要求。
4 执行器箱体尺寸优化
第一次设计的加强筋的截面尺寸是根据经验设计的,为了得到更佳的材料布局以及更轻量化的箱体结构,拟对加强筋截面尺寸进行优化。
4.1 箱体灵敏度分析
箱体灵敏度分析是箱体性能参数(强度、刚度)对设计变量(加强筋截面尺寸)变化的敏感性分析,是优化设计的基础。通过灵敏度分析可获得加强筋截面尺寸对箱体强度、刚度的影响程度,从而确定优化方案[4]。
将加强筋截面宽度H1、深度V3作为优化设计变量,分析设计变量对箱体强度、刚度以及箱体质量的响应灵敏度,分析结果如图11所示。
从图11可以看出:加强筋的宽度H1越大,会使得最大变形变小,而使得最大应力和箱体质量均增加;加强筋的深度V3越大,使得最大变形减小,最大应力减小,但会使得箱体质量增加。

图11 设计变量对响应的敏感度
由以上分析可知,加强筋的深度V3和加强筋的宽度H1对箱体强度、刚度以及箱体质量均有较大影响,表明将深度V3和宽度H1作为优化设计变量是可行的;另外,由于两参数对三个指标的影响并不是统一的正向或者负向,因此在选择优化方案时应给予两参数更大的设计范围。
4.2 轻量化设计
参照灵敏度分析的结果,对设计变量的优化尺寸范围进行设定,加强筋截面宽度H1的设定范围为4.5 mm~7.5 mm,加强筋深度V3的设定范围为3.5 mm~6.5 mm,采用响应面法对箱体质量进行优化。设置箱体质量目标函数最小,箱体变形量目标函数最小,最大应力在0~127.5 MPa范围内最小,计算得到3组最优组合,如表1所示。

表1 优化结果
由表1可知,第2组数据为最优,最大应力最小为110.46 MPa,最大变形为0.135 37 mm,均满足使用要求,箱体质量为3.216 3 kg。对优化结果进行圆整,最终采用的截面宽度H1为4.8 mm,截面深度V3为4.0 mm。
4.3 执行器箱体第二次设计结果对比
根据优化的尺寸,对执行器箱体进行第二次建模,再次验证箱体的强度、刚度。箱体改进前后的性能参数对比如表2所示。
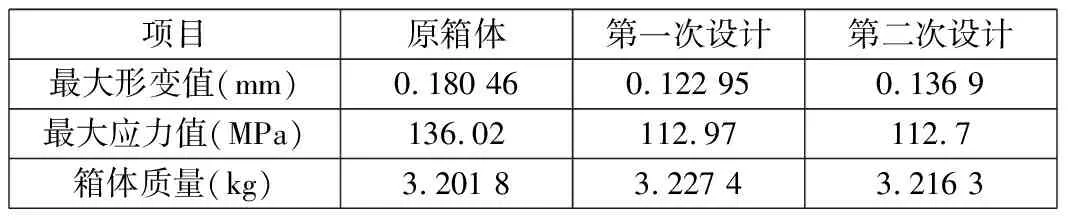
表2 箱体改进前后性能对比
由表2可知:通过尺寸优化,第二次设计的结果和第一次设计结果相比,变形较之前增加了11.4%,但还是小于设计极限0.2 mm;应力较之前下降了0.24%,加强筋截面面积由(6×5) mm2变为(4.8×4) mm2,加强筋质量下降36%,变化显著,表明尺寸优化是十分成功的。
第二次设计的结果与原箱体进行比较,变形下降24.1%,应力下降17.1%,质量较之前增加0.45%。优化之后质量略有增加,应力和变形均大幅下降,结构更加合理,证明优化是有效的和可行的。
5 结论
(1) 基于变密度法,建立了基于柔度最小的箱体优化数学模型,实现了执行器箱体的拓扑优化设计。
(2) 以刚度和体积分数为约束条件对执行器箱体进行拓扑优化,得到了箱体的最佳传力路径。
(3) 对第一次设计的加强筋进行基于响应面的尺寸优化,第二次设计的结果和第一次设计结果相比,加强筋质量降低了36%。
(4) 通过对优化前后执行器箱体结构性能分析可知,优化后的执行器箱体强度、刚度均大幅提高,执行器箱体结构更加合理,证明了优化的可行性。
(5) 为箱体类零件的优化设计提供了借鉴和参考。
